倾斜底板非对称底鼓灾变机理及灾变模式研究

贾永杰

（山西工程职业学院资源与安全工程系，山西太原 030009）

0 引言

底鼓是深埋高应力软岩巷道常遇灾害，底板的轻微隆起会带来严重的安全隐患，造成重大生命财产损失，如阳城煤矿-650 m 南翼综机库发生了1.2 m 的底鼓灾害，巷道底板表面严重隆起、产生大量碎裂岩体，影响了矿井的正常安全生产[1]。因此，诸多学者对底鼓致灾机理进行了研究。姜耀东等[2]将底鼓机理分为4 类：挤压流动性底鼓、挠曲褶皱性底鼓、剪切错动性底鼓和遇水膨胀性底鼓；王卫军等[3]将底鼓机理分为6 类：巷道开挖卸荷后的弹塑性变形、巷道两帮在垂直集中应力下挤压底板变形、底板的破裂碎胀性变形、底板岩层的流变性导致其体积增大、底板拉应变及两帮下沉和水对底板岩层的作用；华心祝等[4]将底鼓全过程分为滑移-弯曲线形成期、剪切错动破坏期、剪切破断期、挤压流动期和离层期5 个阶段；钟祖良[5]、汪洋[6]和邓涛[7]等采用连续介质力学推导了底板岩层压曲、膨胀、扩容和流变引起的底鼓量理论计算公式；康红普[8]等认为底鼓是由失稳的底板岩层向巷道内压曲、偏应力下的扩容和岩体遇水膨胀等造成的；孙晓明等[9]基于欧拉公式，利用压杆稳定理论、摩尔库仑准则和挠曲破坏力学模型，提出了考虑巷道顶板强度的底板破坏机理。

总结已有研究成果可知，当前底鼓力学机理研究大都针对均质各向同性底板岩体，底鼓量呈中间大、两端小的左右对称特征[10]。然而，各向异性或层状岩体广泛分布于沉积岩层或煤系地层中[11]，在这类岩体中开掘巷道时可能会产生非对称底鼓灾害。一方面，当前对倾斜层状底板引起的非对称底鼓研究极少，使得该类底板岩层的底鼓灾变机理研究不足；另一方面，当前大都采用单一的连续性数值方法（如有限差分法[12-13]和有限元法[14]等），难以模拟底板岩层裂隙萌生、扩展贯通、围岩体滑移剪胀、碎胀扩容、破碎岩块间的接触挤压及破碎块体宏观运动全过程，难以揭示底板岩层破裂碎胀孕育演化灾变全过程机制；此外，当前对巷道底板非对称变形的研究大都基于各向同性假设[14-15]，未反映岩体各向异性或横观各向同性特征。

因此，本文将采用有限元-离散元耦合数值模拟方法（FDEM） 研究倾斜底板岩层非对称底鼓灾变机制及对灾变模式的影响。首先，介绍了FDEM数值模拟基本原理及层状岩体和巷道开挖模拟原理；随后，对所需输入参数进行了标定；其次，研究了倾斜底板非对称碎胀大变形的致灾机理；最后，研究了岩层倾角对倾斜底板非对称底鼓模式的影响。

1 参数标定

准确的输入参数是确保模拟结果可靠性的前提，采用不同倾角岩样的单轴压缩模拟进行输入参数标定，数值模型如图1 所示。岩层倾角β分别为0、22.5°、45°、67.5°和90°，层厚10 mm，模型高100 mm、宽50 mm，网格尺寸1.6 mm，加载速率0.1 m/s，计算时步1×10-9s，岩样宏观力学参数来源于文献[16]，节理罚值Pf[17]、法向接触刚度Pn[18]及切向接触刚度Pt[19]取值方法可见相应文献，本节需对I 型和II 型断裂能进行标定。

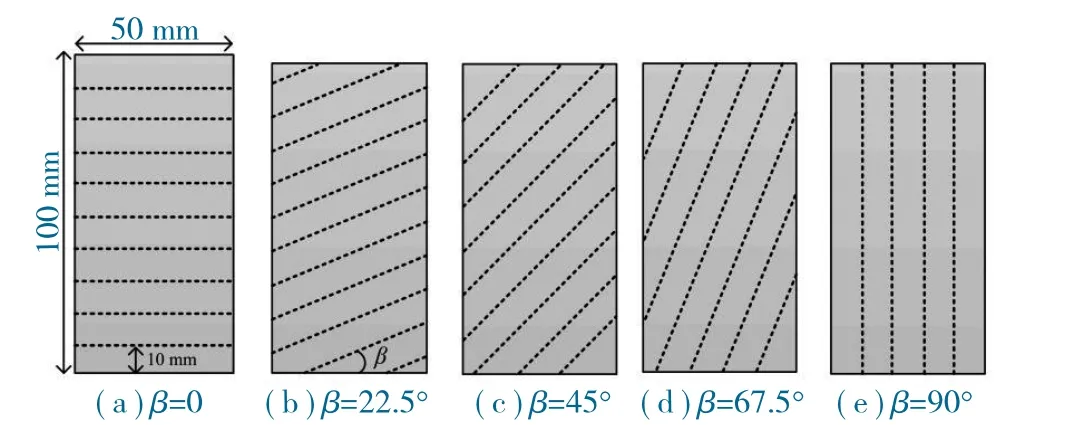
图1 单轴压缩数值模型Fig.1 Numerical models of uniaxial compression

当采用表1 断裂能及其他参数时，得到图2 模拟结果。一方面，岩样单轴抗压强度σc随岩层倾角β的变化关系与Ajalloeian 等人[20]通过大量不同岩性的室内单轴压缩试验得到的结果极为相近，即0 倾角和90°倾角的抗压强度相近，但0 倾角的抗压强度略高于90°倾角，而倾角约为时其强度最低，如图2（a） 所示；另一方面，不同倾角的岩样破裂模式与Tien 等人[21]室内单轴压缩试验结果相近，即对于较小倾角的岩样，层理面对岩样破裂模式影响较小，其破坏模式与各向同性岩样相近，均大致沿着理论破断角发生主剪切破坏，并产生少量拉伸裂隙，但当倾角增大时，主要发生沿层理面的剪切滑移破坏，而当倾角为90°时，主要发生沿层理面的拉伸劈裂破坏，如图2（b） 所示。上述模拟结果表明，表1 的输入参数是合理的，且证明FDEM 在模拟岩石材料变形破坏方面是可靠的。

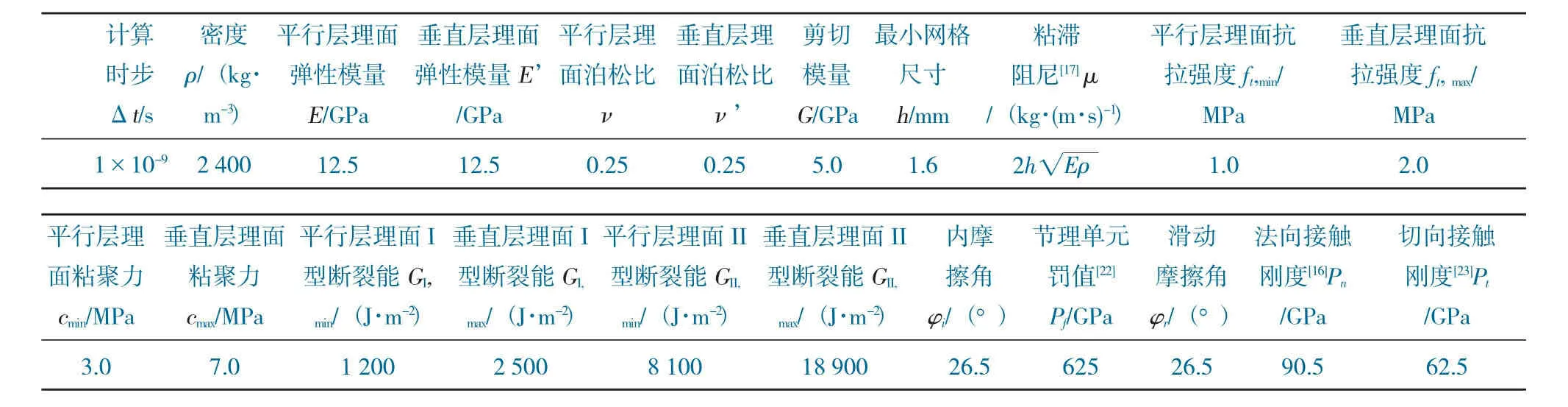
表1 FDEM 模拟参数[16,26]Table 1 Simulation parameters of FDEM[16,26]

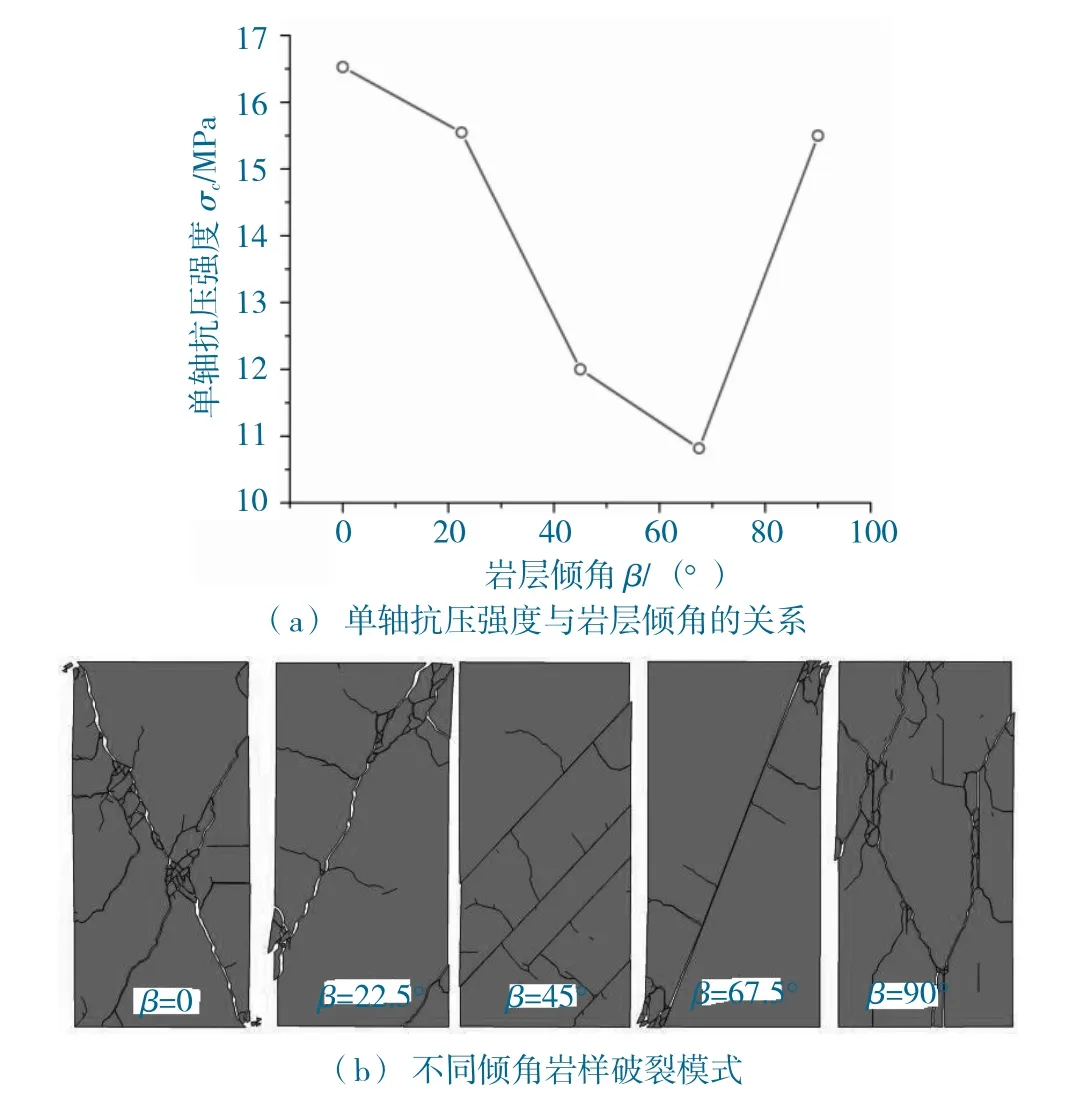
图2 单轴压缩数值模拟结果Fig.2 Simulation results of uniaxial compression

2 倾斜底板岩层底鼓灾变机制FDEM 数值模拟

2.1 巷道开挖数值模型

倾斜底板巷道开挖数值模型如图3 所示，以倾角15°为例，底板为层状倾斜（即横观各向同性）岩体、顶板为各向同性岩体，顶、底板岩层的这种接触关系为角度不整合接触。将模型划分为远场区、网格细化区及巷道核心材料区。以1 m 层厚为例，数值模型直径为100 m，在模型中开挖宽5 m、半径2.5 m 的直墙半圆拱形巷道，网格细化区直径30 m，对于底板岩层而言，在网格细化区内，采用相同的网格尺寸h（h=0.16 m[11]），且应确保所有的裂隙均在网格细化区内扩展，因此，层状底板的层理面可仅在网格细化区内显式表征，在远场区内依然采用各向异性本构模型，但无需绘制出层理面。顶板岩层强度足够大以致不发生破裂，所以针对底板岩层破裂机制和破裂模式开展研究[27]。

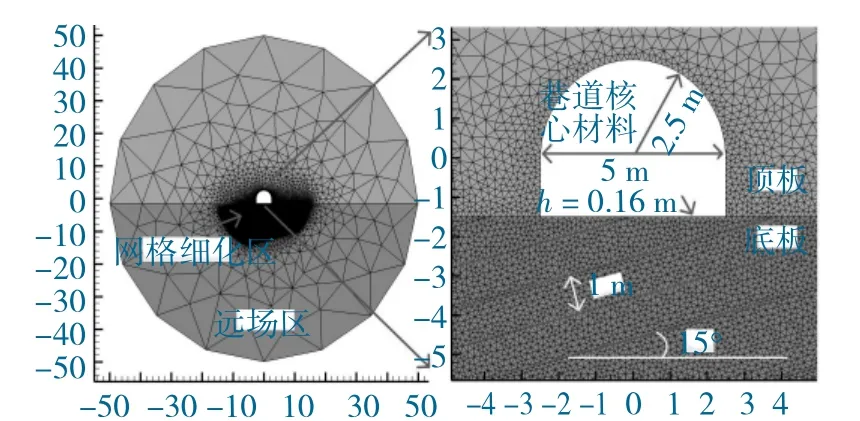
图3 倾斜底板岩层巷道开挖FDEM数值模型Fig.3 FDEM numerical model of roadway excavated in inclined floor rock mass

2.2 底板岩层破裂碎胀大变形过程模拟结果

水平和垂直地应力均设为26 MPa，即静水压力状态，岩层倾角设为15°，数值模型如图3 所示，输入参数（表1），计算时步Δt=8×10-8s。

随着巷道核心材料弹性模量及粘滞阻尼的逐步软化，倾斜底板岩层破裂过程如图4（a） ～（f）所示。

图4 底板岩层破裂碎胀大变形过程Fig.4 Large deformation process of floor rock mass

在软化卸荷初期，底板首先在左、右两帮角发生剪切破坏，并向底板深部和两侧扩展，如图4（a） 所示；随着核心材料的持续软化卸荷（真实巷道开挖表现为掌子面向前推进），一方面围岩裂隙主要以共轭剪切及沿层理面的剪切形式不断向围岩深处扩展，即深部完整岩体相继发生破裂，表现出渐进破裂特征[25]；另一方面，浅部已破裂的岩体在更深部块体的接触挤压下发生剪胀滑移和宏观翻转运动。在翻转运动过程中，长条状的岩块发生垂直层理面的拉伸破断，脱离围岩母体，最初平行的层理面不再平行，碎裂岩体不断向巷道空间呈现整体缓慢“挤压”态势，使得巷道断面空间减小，发生底鼓灾害。

由于核心材料的软化卸荷，巷道表面围岩发生径向应力降低、切向应力升高现象，当升高的切向应力超过该围压下的岩体强度时，围岩发生破裂，破坏后的巷道表面围岩无法承载巨大的切向集中应力，使得切向集中应力向深处完整围岩体转移并造成更深部的完整岩体相继发生破裂，直至卸载完成后在围岩深处切向集中应力与岩体强度达到极限平衡状态，裂隙停止扩展，这是因为径向应力由巷道表面向围岩深处增大[26]，岩体强度随之升高，如式（1） 所示：

式中：σ1、σc和σ3为三轴抗压强度、单轴抗压强度和围压，对于巷道围岩，围压表现为径向应力。

2.3 底板岩层位移场分析及碎胀大变形机理

底板岩层位移如图5 所示，可将围岩体分为碎胀区和破裂区，其交界面大致沿着垂直层理面的拉伸裂隙。在碎胀区范围内破碎的岩体产生了剪胀滑移和翻转运动，碎裂块体已脱离了围岩母体，即离层现象，块体间发生了显著的张开现象，产生宏观空隙，将对支护结构产生松散压力，是底鼓灾变的主要驱动源；而破裂区范围内的岩体仅发生断裂，未有明显的宏观运动，块体间紧密贴合、裂隙处于闭合状态，未与底板围岩母体发生离层，对底板变形量的贡献较小，倾斜层状底板位移呈显著的左右不对称特性（左侧位移小、右侧位移大），右侧最大底鼓量约为0.7 m。

图5 碎裂块体宏观运动态势、碎胀效应及围岩位移场Fig.5 Movement and fracture-swelling effect of fragments and the displacement field of floor rock mass

根据模拟结果可知，底板大变形主要来源于：①深部破断岩块对浅部碎裂块体的接触挤压效应，并使得浅部块体发生剪胀滑移及翻转运动，是为碎裂块体的宏观运动；②剪胀过程和块体的不均匀运动（每个块体的运动速率和方向都不相同） 使得最初吻合的块体不再啮合、产生宏观空隙，使得松散岩块产生体积膨胀现象，是为碎胀效应；③此外，巷道开挖卸荷后围岩体亦产生弹性变形恢复，即块体自身会发生体积恢复，但它对底板大变形的贡献是微小的。

2.4 底板岩层应力场分析及底鼓力学模型

分析巷道开挖后围岩应力场分布特征，揭示底板岩层碎胀大变形灾变力学机理。在极坐标下，围岩径向应力和切向应力根据式（2） 得到[26]：

式中：σr、σθ为极坐标系下的径向应力和切向应力；θ 为极坐标与x 轴正方向的夹角，以逆时针为正；σxx、σyy和τxy分别为笛卡尔坐标系下的水平应力、垂直应力和剪应力。

围岩最终径向应力和切向应力如图6（a） ～（d） 所示，可知，由于开挖卸荷，巷道围岩发生了径向应力降低和切向应力升高现象，即为降围压、升轴压的三轴压缩力学模型，正是在这种综合作用下，围岩发生了拉伸、剪切破裂。

图6 巷道围岩应力场Fig.6 Stress fields of the roadway surrounding rock mass

对于切向应力而言，其在顶板和底板裂隙尖端集中，且裂隙尖端的集中应力形成压力拱，使得围岩最终达到平衡状态，裂隙不再往更深处扩展。然而，对于巷道两帮岩体而言，切向应力被释放，不再对底板产生挤压作用，如图6（b） 所示。此外，底板围岩水平和垂直应力场如图6（c） ～（d） 所示，可知：对于水平应力而言，其在底板下方裂隙尖端集中，而底板两侧的水平应力被释放；对于垂直应力而言，其在底板两侧裂隙尖端集中，而巷道两帮的垂直应力被释放。

因此，图7 所示的现有底鼓力学模型存在如下不足：①认为底鼓主要由于两帮垂直应力和底板两侧水平应力引起的，而实际上这两处的垂直应力和水平应力分别被释放了，也就是说，图7 所示力学模型仅考虑了初始地应力状态，并强调初始地应力的作用，是一静态力学模型，而未考虑巷道开挖引起的围岩应力场的动态演化；②难以解释图6（b） 虚线椭圆的剪切裂隙，因为根据图7 所示力学模型，底板裂隙应为向巷道内凹，而非如图6（b）的向底板深部外凸；而实际上，底板裂隙尖端的外凸型形态已在诸多室内模型试验中得到验证[27-28]；③现有底鼓力学模型仅考虑了底板变形的最终形态，忽略了底鼓过程的渐进性及时效性。本文提出的巷道开挖引起的降围压、升轴压三轴压缩动态力学模型能够解释围岩裂隙网络扩展机制及围岩应力场的动态演化过程。

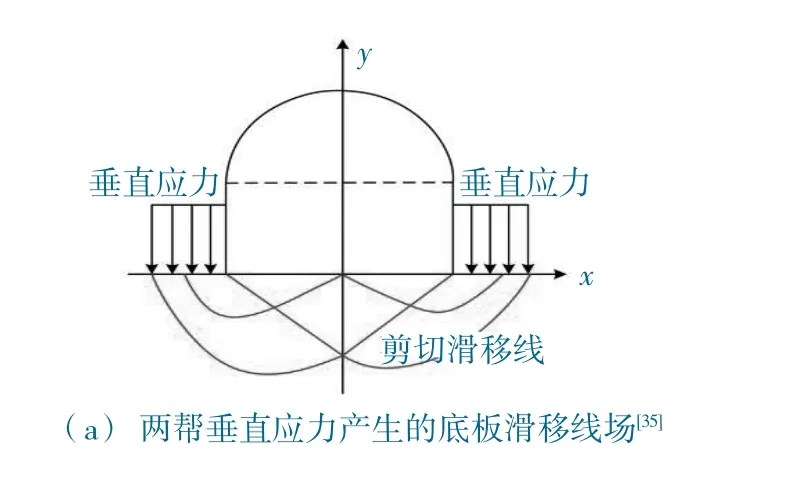
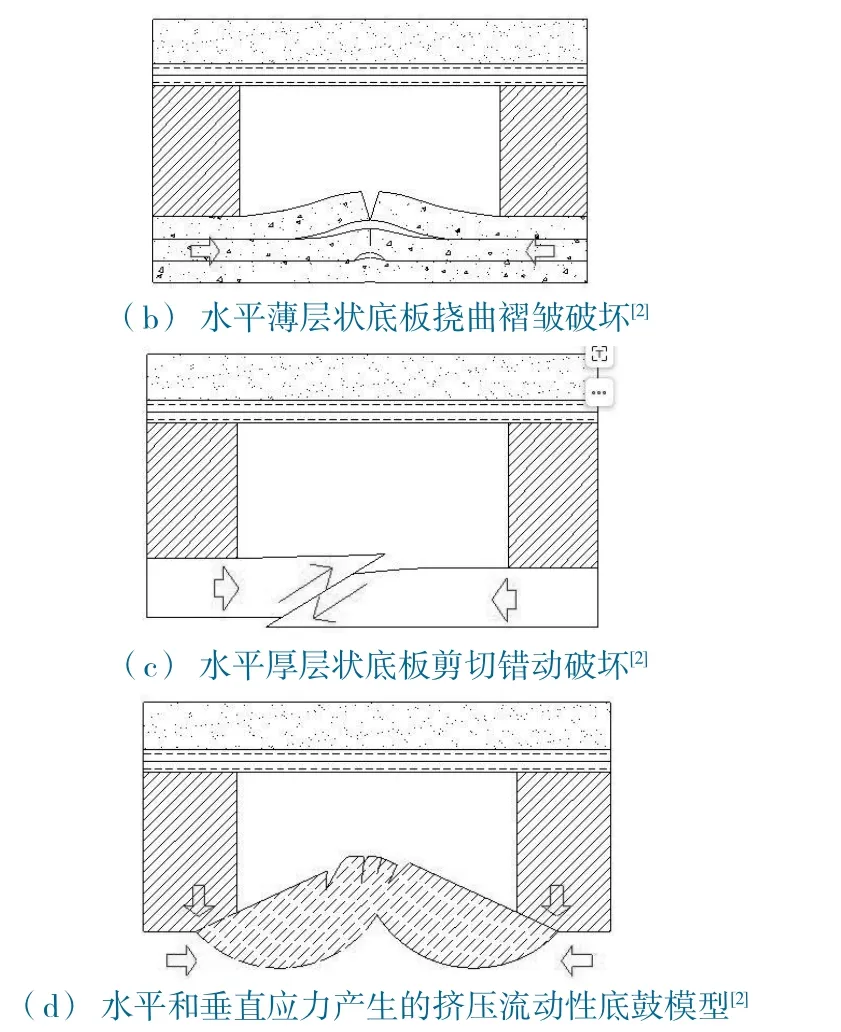
图7 现有的底鼓力学模型Fig.7 Current mechanical models of floor heave

3 岩层倾角对底鼓灾变模式的影响

将底板岩层倾角分别设为0、15°、30°、45°、60°、75°和90°，研究底板岩层倾角对底鼓灾变模式的影响，得到图8 的模拟结果。

图8 不同倾角的底板岩层底鼓模式Fig.8 Floor heave modes of different dip angles

随着底板岩层倾角的变化，底板破裂碎胀大变形呈现如下相似性：①随着倾角变化，底板岩层均产生两组共轭剪切裂隙，分别垂直和平行于层理面，如图8 及图4（f） 箭头所示，此外，还伴生大量平行于各自层理面的剪切滑移裂隙；②尽管底板岩层裂隙网络形态和巷道底板表面位移模式不同，但均可采用如图6（b） 的环形切向集中应力模型解释底板岩层的破裂碎胀大变形，并简化为降围压、升轴压的三轴压缩力学模型，即底鼓灾变机制是相同的，底板岩层的环形切向集中应力是造成围岩发生破裂碎胀大变形的应力驱动源；③此外，根据围岩位移场，均可将围岩分为碎胀区和破裂区，如图9 所示，碎胀区是底板变形的主驱动源，而破裂区对底板变形量贡献微弱。

图9 不同倾角底板岩层位移场Fig.9 Displacement field with different dip angles

然而，随着底板岩层倾角的变化，巷道底板呈现出不同的底鼓模式，具体如下：①对于0 倾角，即水平层状底板，底板呈现典型的中间高、两侧低的对称性底鼓模式，与各向同性底板岩层底鼓模式相近[1]，所不同的在于水平层状底板除了共轭剪切破裂外，还存在沿层理面的剪切滑移裂隙和垂直层理面的拉伸裂隙，最终呈现一种复合破裂模式[11]；②对于15°和30°倾角的底板岩层，底板呈现右侧高、左侧低的非对称底鼓模式；③对于45°和60°的倾角底板岩层，底鼓的非对称特征减弱；④对于75°和90°的倾角底板岩层，巷道底板表面呈现对称特征，底板表面岩体完整；⑤对于不同倾角的底板岩层，虽然根据位移场仍可划分为碎胀区和破裂区，但碎胀区的形态随着底板岩层倾角的变化发生相应变化，总体上，碎胀区与破裂区交界面凸向层理面垂直方向，如图9 和图5（b） 所示。

4 结论

层状岩体在煤系地层中广泛分布，当倾斜层状岩体位于深部高应力巷道底板时，可能引起底板非对称底鼓灾害。采用FDEM 研究了层状底板底鼓灾变机制，并研究了底板岩层倾角对灾变模式的影响，提出了对这类底鼓灾害控制的优化措施，得到如下结论。

（1） 应力驱动型的倾斜底板岩层底鼓灾变机制为底板岩层的碎胀性渐进挤压变形，表现为巷道开挖引起径向应力降低、切向应力升高，即为降围压、升轴压的三轴压缩力学模型；共轭剪切裂隙网络、平行于层理面的剪切滑移裂隙和垂直层理面的拉伸裂隙持续向深部扩展，岩块间的剪胀滑移和碎裂块体自身翻转运动引起了底板岩层的持续性渐进大变形，可将底板破裂围岩分为碎胀区和破裂区，前者是底板大变形的主要贡献源。

（2） 岩层倾角对底鼓灾害模式具有重要影响，表现为：对于15°～30°的底板岩层，呈现显著的非对称底鼓；对于45°～75°倾角的岩层，非对称特征减弱；对于0 或90°倾角的底板岩层，底板大变形是左右对称的；然而，随着底板岩层倾角的变化，底鼓灾变机制和裂隙网络形态保持不变，均呈现两组共轭剪切裂隙沿平行层理面方向和垂直层理面方向扩展特征。