计及预测误差时变相关特性的新型电力系统爬坡容量需求分析方法

任相霖，张粒子，黄弦超

（华北电力大学电气与电子工程学院，北京 102206）

0 引言

面对日益突出的能源危机、环境污染和气候变化等问题，构建以可再生能源为主的新型能源供应体系已成为国际社会共识。国际能源署（IEA）表示未来10年全球电力需求增长的80%将由可再生能源来满足［1］；截至2020年底我国风电和光伏装机均已突破250GW，到2030 年和2050 年可再生发电量占比可分别达到30%和60%［2］。然而可再生能源发电出力的随机性、波动性和间歇性对电力系统安全经济运行带来了新的问题及挑战，新型电力系统需在运行过程中预留一定灵活性爬坡容量。2022年国家发改委和国家能源局联合发布《加快建设全国统一电力市场体系的指导意见》［3-4］，要求提升电力市场对高比例新能源的适应性，并提出新能源比例较高的地区可探索引入爬坡等新型辅助服务。国内对爬坡辅助服务的研究尚处于起步阶段，对其交易机制及出清模型、爬坡需求分析及定价机制等方面的研究，是当前电力市场领域亟待研究的重要方向［5］。

新型电力系统所需要的爬坡容量由两部分组成：一是应对系统相邻时段的净负荷波动而产生的确定性爬坡容量［6-8］，二是为了应对系统净负荷预测误差而产生的不确定性爬坡容量［9-11］。确定性爬坡容量由净负荷预测值的波动情况所决定，可通过负荷预测方法［12］获得；不确定性爬坡容量由净负荷预测误差所决定，在计算分析中应明确预测误差与预测值的相依结构，以体现净负荷预测值的差异对不确定性爬坡容量的影响［13-14］。Copula理论能够有效刻画多变量间的复杂相依结构，在构建联合分布时具有独特的优势，近年来多用于可再生能源出力的相关性分析中。文献［15］以多元正态分布函数和Copula函数为基础提出了一种考虑多风电场出力时空相关性的联合出力场景生成方法。文献［16］将风电预测值与预测误差建立动态相关性联系，提出了计及预测误差动态相关性的多风电场联合出力不确定性模型。文献［17］考虑到两相邻风电场出力的相关强度并非一成不变，采用时变Copula函数来分析风电出力时变相关性。文献［18］基于Copula理论实现了任意点预测对应的光伏实际出力的条件概率分布估计。目前对Copula理论的研究多集中在多风电场联合出力预测以及风光联合出力预测上，鲜有考虑因净负荷日变化特性而导致的净负荷预测误差与预测值的时变相关性，并将此应用在爬坡容量需求的确定中。

本文首先明确灵活性爬坡容量的构成，分析系统所需的爬坡容量与净负荷预测误差的关系；然后应用动态Copula函数及条件概率理论提出计及预测误差时变特性的爬坡需求分析方法；最后基于我国某西部电网2020年实际运行数据进行算例验证，验证本文提出的爬坡需求分析方法的有效性和正确性。

1 爬坡容量的构成

以可再生能源为主的新型电力系统面临着可再生能源出力波动性较大和预测准确性不高的双重问题，因而系统所需的爬坡容量不仅仅需要应对净负荷波动，还需要考虑净负荷的预测误差，如图1所示。

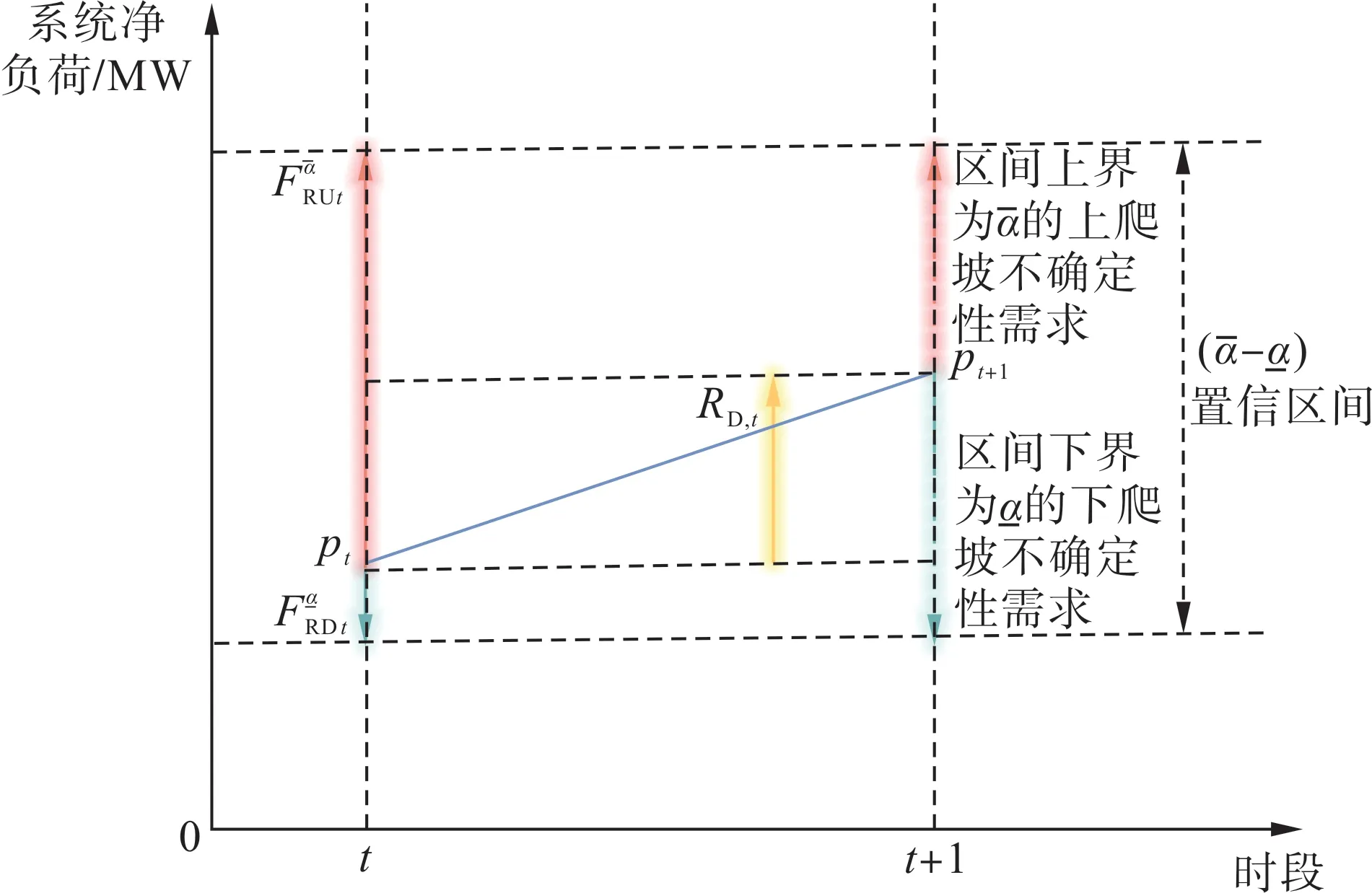
图1 爬坡容量构成示意图Fig.1 Schematic diagram of ramp capacity composition

系统所需要的爬坡容量计算公式如下所示。

爬坡不确定性需求与置信区间上下界之间的关系由式（2）—（3）反映。

目前基于历史预测误差数据统计得到的爬坡不确定性需求测算方法［9］无法体现不同净负荷预测值下预测误差不同的概率分布，因而为了合理量化爬坡不确定性需求，需要刻画净负荷预测误差与预测值的相依结构，在此基础上对系统净负荷预测误差进行概率估计。

2 基于动态Copula 理论的预测误差条件概率分布分析

2.1 Sklar定理和Copula理论

Sklar 于1959 年提出的Sklar 定理是Copula 理论的基础，该定理表示：对于含有n个随机变量x1，x2，…，xn的联合分布，可通过这个n变量的边缘分布函数和对应的Copula 函数来进行描述［22］。根据Sklar 定理，Copula 函数的联合分布函数和联合密度函数表达式分别为：

式中：F(xn)和f(xn)分别为xn的边缘概率分布和边缘概率密度；C(⋅)和c(⋅)分别为联合概率分布和联合概率密度。

Copula概率分布函数与对应的Copula概率密度函数的关系如式（6）所示。

Copula 函数建立了边缘分布和联合分布的映射关系，利用Copula理论可以将对变量的联合分布建模转化为对变量边缘分布和相依性结构分别建模，该理论已被广泛应用于统计学、金融领域，近年来开始应用于电力系统，主要进行风光出力的相关性分析及不确定建模。

2.2 Copula函数

Copula 函数主要分为椭圆函数族和阿基米德函数族两大类，其中Gaussian-Copula 函数和t-Copula函数属于椭圆函数族，Gumbel-Copula 函数、Clayton-Copula 函数和Frank-Copula 函数属于阿基米德函数族，不同类型的Copula函数具有不同的函数结构以及不同的尾部特性，用于刻画不同类型的相依关系。

考虑到净负荷预测误差与预测值的相依关系具有时变特征，本文采用Patton 提出的动态Copula 理论，通过引入类似于ARMA（1，10）的过程，将传统Copula 的静态相关性参数动态化［20］。以二元动态Gaussian-Copula（也称N-Copula）函数为例，其动态相关性参数的演进方程为：

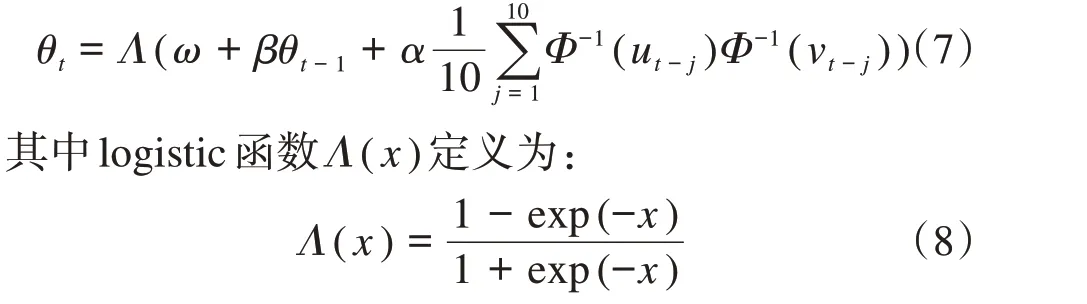
式中：ω、β和α为动态Copula 演进方程的待估计参数；Φ-1(⋅)为标准正态累计分布的逆函数；θt-1为t- 1 时刻的动态相关参数；ut-j和vt-j为边缘分布函数。

求解过程将演进方程带入Copula函数中，通过极大似然估计法估计演进方程参数ω、β和α，进而可计算动态相关参数序列θt，从而获得各时段确定的Copula模型。

2.3 预测误差条件概率模型

由于风速、太阳辐射及云层遮挡等气象因素的随机特性，净负荷预测误差和其预测值之间并没有一个确定性的关系，可视为一对具有相关性的随机变量，可以采用Copula函数进行两者的相依结构模型构建。设e为预测误差，p为预测值，则根据式（4）和式（5），e和p的联合概率累计分布函数和联合概率密度函数可以写为：

式中：fE(e)和fP(p)分别为预测误差和预测值的边缘 分 布 概 率 密 度 函 数；c(FE(e)，FP(p)|θt) 为Copula密度函数。

在调度计划确定过程中，净负荷的预测值作为已知量，根据所拟合的预测误差与预测值之间的相依结构模型，即可推导出各预测值下的预测误差分布情况。因此，给定预测值p=p̂，则预测误差的条件概率密度函数fE|P(e|p)可以表示为：

式中p̂为给定的净负荷预测值。

式（11）表明，预测误差条件概率分布计算可以转变为预测误差边缘概率密度以及预测误差与预测值的Copula密度函数的计算。

3 爬坡需求分析方法建模过程

根据式（11），对预测误差的条件概率分布估计可以转化为对预测误差的边缘概率密度函数fE(e)和Copula密度函数c(FE(e)，FP(p)|θt)分别进行建模。其中预测误差的边缘概率密度函数fE(e)或累积分布FE(e)可以通过对历史净负荷预测误差数据进行统计得到；预测值的累计分布FP(p)可以通过对净负荷预测历史数据的统计得到。

Copula 函数拟合的关键在于参数估计，目前估计方法主要包括直接估计法和分步估计法，两者的主要区别在于前者是一步估计出变量的边缘函数和Copula函数的未知参数，而后者是先估计出变量的边缘函数参数，再进行Copula函数参数估计，这可以有效地节省运算空间，因此本文采取分步估计法。由于净负荷数据总量大、影响因素复杂，本文将采用核密度估计法进行预测误差以及预测值的边缘分布估计［16］。核密度估计法表达式为：

式中：Kh为核函数；T为序列长度。

本文采用极大似然估计法对动态Copula函数演进方程参数进行估计，首先将演进方程代入似然函数，构建基于演进方程参数的似然函数，然后对演进方程参数进行极大似然估计，具体似然函数如下。

式 中α̂、β̂、ω̂为 待 求 演 进 方 程 参 数；FE(et)和FP(pt)分别为净负荷预测误差的边缘概率分布函数和净负荷预测值的边缘概率分布函数；c(FE(et)，FP(pt))为净负荷预测误差和预测值的联合概率密度函数。

另外，因为净负荷的变化特性会影响估计日的预测误差概率分布情况，因而本文采取欧式距离比选方法在历史数据中选出估计日的最优相似日，并将最优相似日作为输入进行估计日的动态相关参数测算。

具体建模步骤如下，流程图如图2所示。

图2 建模流程Fig.2 Moduling process

步骤1：标幺化原始时间序列数据，获得历史数据时间序列e、p；

步骤2：计算核密度估计函数，得到边缘分布函数fE(e)、FE(e)、fP(p)、FP(p)；

步骤3：根据估计日的净负荷预测值，通过欧式距离比选出最优相似日；

步骤4：建立动态Copula 函数，构建基于动态相关参数θt的似然函数，即式（13）；

步骤5：将日前40 d 的预测误差和预测值以及估计日的最优相似日的预测误差和预测值作为输入序列代入演进方程，建立演进方程参数α、β、ω与动态相关参数θt的映射关系，即式（7）；

步骤6：将演进方程带入似然函数，构建基于演进方程α、β、ω的似然函数，即式（14）；

步骤7：求取极大似然估计值，利用极大似然估计法对演进方程参数进行估计，即式（15）；

步骤8：将计算出的α、β、ω和输入序列代入演进方程进行估计日的动态相关参数θt测算，至此得到了估计日各个时段确切的相依结构；

步骤9：根据预测误差条件概率模型，即式（11），测算出估计日预测值条件下预测误差的概率分布情况；

步骤10：基于此得到估计日的爬坡不确定性变量需求概率分布情况，将其与由净负荷预测值波动所决定的爬坡确定性变量需求叠加即可得到该日的爬坡容量总需求概率估计结果。

4 算例分析

4.1 基础数据

本文算例采用我国某西部电网2020 年风光出力实测数据及其日前预测数据、负荷实测数据及其日前预测数据，颗粒度为15 min，共计35 136 组数据形成净负荷实测数据和净负荷日前预测数据，以此作为本文的数据基础。为将正负预测误差与上下爬坡需求形成对应关系，本文预测误差数据由实测数据减去预测数据得到。

4.2 相关性系数测算及分析

目前对于预测误差的研究大多针对的是预测误差的绝对值，不区分正负，但研究发现正负预测误差与预测值的相关性系数差距很大（如表1所示，表1为9月17日至10月26日正负净负荷预测误差与净负荷预测值的相关性系数测算结果），其相依关系有很大差异，这与地方风光消纳政策具有一定的关系，如若风光出力预测偏高申报势必造成净负荷负预测误差有所减小。上爬坡容量不足引起切负荷损失，下爬坡容量不足引起弃风光甚至切机损失，对于成本价值不同的上/下爬坡测算应该进行区别测算。

表1 正负预测误差与预测值的相关性系数Tab.1 Correlation coefficients for positive and negative forecast errors

此外，表1 中的相关性系数均为负值，表示净负荷预测值越大对应的预测误差越小。这与样本电网的电源结构以及负荷特性相关，当净负荷预测值较大时，往往是风光出力较小的时刻，因而其净负荷的预测误差也就越小。

4.3 Copula函数的选择

Copula 函数拟合效果可通过赤池信息量准则（AIC，其指标值用AIC表示）和贝叶斯信息量准则（BIC，其指标值用BIC表示）进行表征。

式中：k为模型参数数量；L为极大似然估计值；n为样本数量。AIC 和BIC 指标可体现模型复杂程度和拟合优劣性，其数值越小表示模型越简洁、拟合效果越优。

为了更好地表达净负荷预测误差与预测值之间的关系，本文分别采用Gumble-Copula、SJCCopula、Gaussian-Copula 对风光出力较小场景（10月27日）以及风光出力较大场景（10月29日）进行了测算分析。

从表2 和表3 可以看出，Gaussian-Copula 函数具有相对更优的拟合效果，故本文选用Gaussian-Copula 函数。

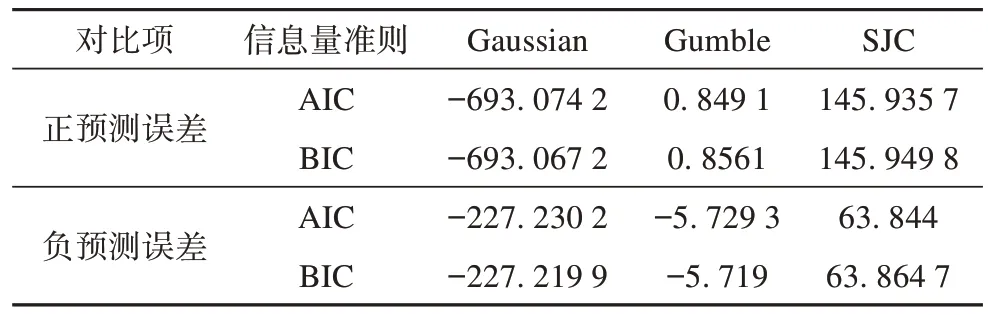
表2 不同Copula函数拟合效果对比（10月27日）Tab.2 Comparison of fitting effects of different Copula functions （October 27）

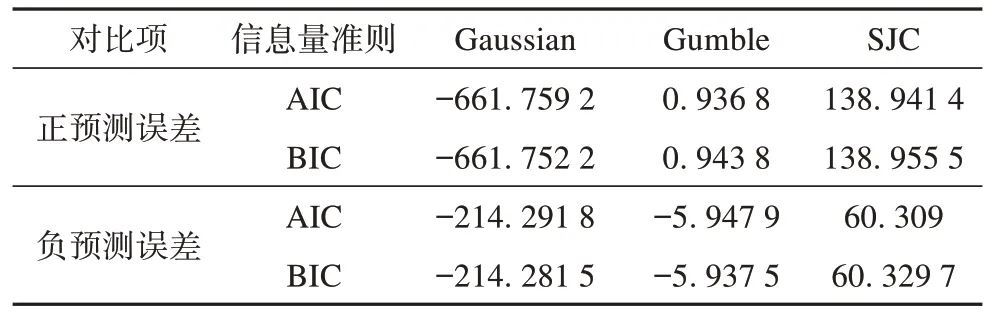
表3 不同Copula函数拟合效果对比（10月29日）Tab.3 Comparison of fitting effects of different Copula functions （October 29）

4.4 预测误差条件概率测算

为对比分析本文所提模型的优越性，选取3 种概率区间测算方法。

方法一：不分时段进行静态Copula函数拟合；

方法二：区分时段进行静态Copula函数拟合；

方法三：进行动态Copula 函数拟合（本文测算方法）。

由于风光出力大小严重影响预测误差，因而利用这3 种方法分别针对风光出力较小场景（10 月27日）以及风光出力较大场景（10 月29 日）进行算例测算。演进方程参数α、β、ω的估计结果如表4 和表5 所示。其动态相关参数θt的测算结果如图3 和图4所示。预测误差条件概率测算结果如图5所示。

表4 风光出力较小场景下演进方程参数Tab.4 Evolution equation parameters in the scenes of low wind and photovoltaic power

图3 风光出力较小场景下Copula函数相关参数测算结果Fig.3 Related parameters of copula function in the scenes of low wind and photovoltaic power

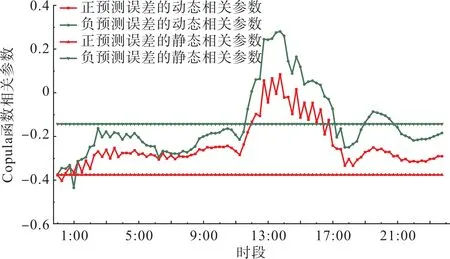
图4 风光出力较大场景下Copula函数相关参数测算结果Fig.4 Related parameters of copula function in the scenes of high wind and photovoltaic power

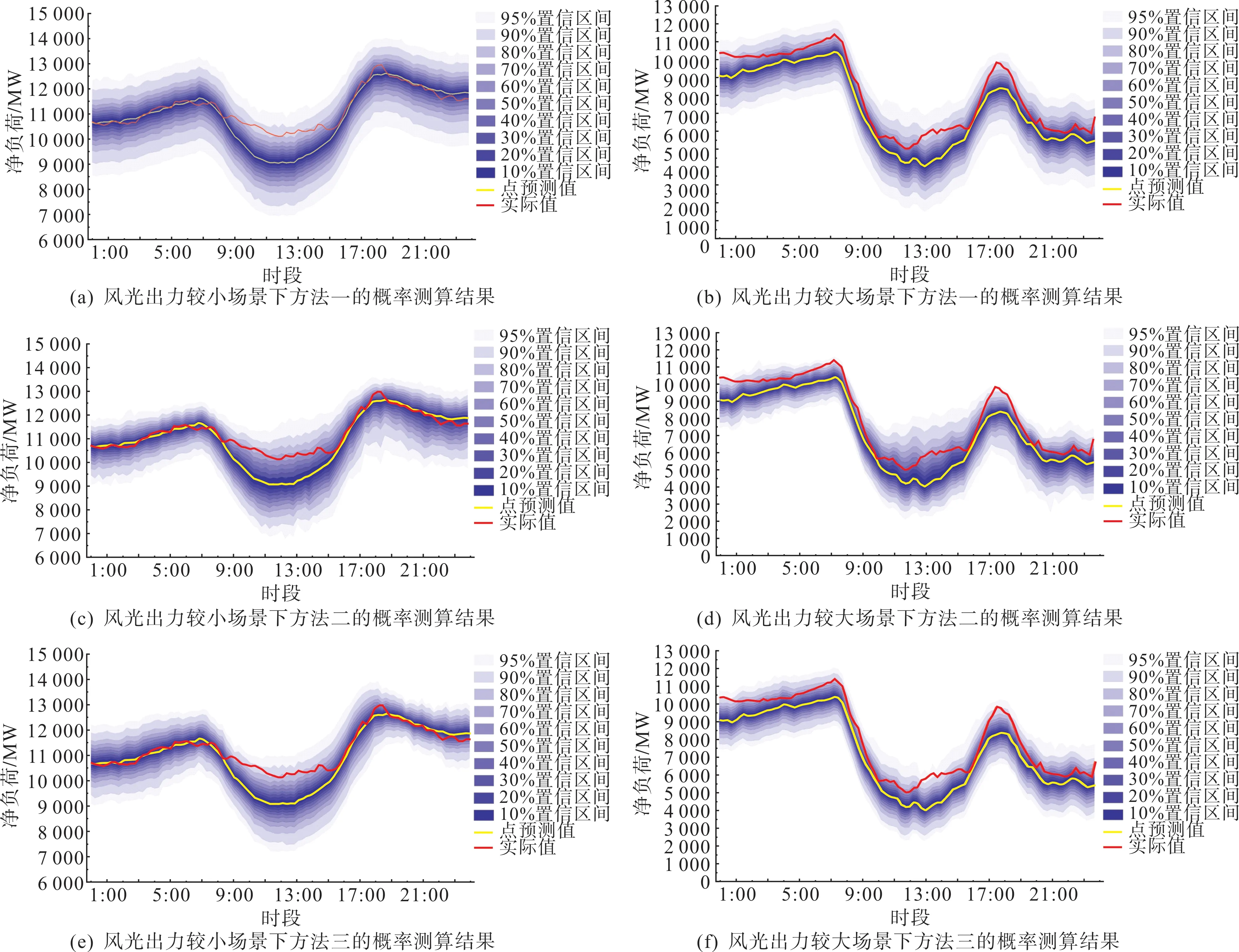
图5 算例测算结果展示Fig.5 Display of the calculation results

由图5 可以看出方法三测算结果的置信区间宽度小于方法二和方法一测算结果的置信区间宽度。以95%置信度为例，在风光出力较小场景下方法三测算结果的区间上界比方法一的区间上界最多可降低724 MW（21：30）、区间下界最多可升高1 308 MW（19：45），方法三测算结果的区间上界比方法二的区间上界最多可降低1 397 MW（12：45）、区间下界最多可升高1 640 MW（19：45）；在风光出力较大场景下方法三测算结果的区间上界比方法一的区间上界最多可降低981 MW（12：45）、区间下界最多可升高820 MW（18：45），方法三测算结果的区间上界比方法二的区间上界最多可降低2 078 MW（12：45）、区间下界最多可升高978 MW（19：30）。由此可见，在同样置信度水平下，应用本文所提出方法由于计及了预测误差的时变相关性，更加精确地刻画了净负荷预测误差与预测值之间的关联关系，从而有效地降低预测误差的不确定性。

4.5 评价指标与方法对比

4.5.1 评价指标

目前常用的概率预测结果评价指标主要包括可靠性指标、锐度指标和综合性能分数指标［23］。

1） 可靠性指标

可靠性指标衡量的是预测概率分布与预测对象实际分布的偏差，预测结果只有在保证可靠性要求的前提下才能在可再生能源高占比电力系统分析中得到有效应用。通常采用平均覆盖误差（average coverage error，ACE）衡量其可靠性，ACE 计算公式如式（18）所示，其值越小，说明预测区间可靠性越高。

2） 锐度指标

锐度指标衡量的是预测概率分布的集中程度，通常可用平均区间宽度（average width，AW）来衡量预测区间的锐度性能，AW 计算公式如式（20）所示，其值越小的区间预测效果越优。

3） 综合性能分数指标

综合性能分数用于衡量概率预测总体性能，其中Winkler 分数是区间预测中常用的综合性能分数指标，Winkler 分数计算公式如式（21）所示，其值越小表示预测区间综合性能越好。

4.5.2 方法对比

分别对两类场景3 种方法的可靠性指标平均覆盖误差ACE、锐度指标平均区间宽度AW 以及综合性能分数指标Winkler 分数进行计算［24］，以此来对3 种方法的性能进行对比分析。计算结果如表6 和表7所示。

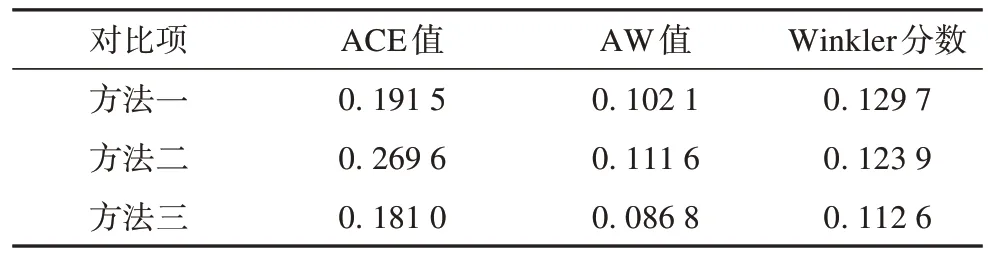
表6 风光出力较小场景下3种方法的评价指标Tab.6 Evaluation indexes of the methods in the scene of low wind and photovoltaic powers

表7 风光出力较大场景下3种方法的评价指标Tab.7 Evaluation indexes of the methods in the scene of high wind and photovoltaic powers

对比3 种方法的评价指标可以看出，风光出力较小的场景下方法三的3 种指标全面占优，而风光出力较大的场景下方法二的可靠性指标ACE 优于方法三，但其余两指标优度不如方法三。方法二和方法三的优越性说明了考虑不同时段预测误差概率分布差异以及其相依关系差异的重要性，方法三利用演进方程将相邻时段的Copula函数的相关参数联系起来，而方案二各时段Copula 函数拟合是割裂的。另外，方法二对风光出力较小的场景不友好，因为该方法相当于牺牲了一定的锐度来确保可靠性，但是对于风光出力较小的场景该方法往往高估了部分时段的不确定性，而导致测算结果过度保守。因此，方法三对于不同净负荷的出力场景的适应性更高，对于净负荷的不确定性刻画更为准确。

4.6 爬坡需求概率分布估计

以风光出力较大的场景为例，根据上节预测误差的概率估计结果以及系统所需的灵活性爬坡容量计算式（1）—（3），对算例各时段的爬坡不确定性需求以及爬坡总需求进行测算，结果如图6—7所示。

图6 爬坡不确定性需求测算结果Fig.6 Estimation results of ramp capacity uncertainty calculation results

图7 爬坡容量总需求测算结果Fig.7 Estimation results of ramp capacity gross demand calculation results

根据爬坡不确定性需求测算结果可以看出，风光出力较大场景下13：00 爬坡不确定性需求显著低于上爬坡不确定性需求（如图6 红框所示），不同时段上/下爬坡不确定性需求具有一定差异性，这与该时段的净负荷预测值以及正负预测误差的相依关系密切相关，因而区分爬坡的方向性进行爬坡需求测算更为细致可靠，可有效地减少由于预测误差而导致的不确定性爬坡容量预留。

从爬坡容量总需求测算结果可以看出，该电网在8：00—10：15 以及18：30—20：30 为下爬坡需求紧迫时段，而在15：45—17：00 为上爬坡需求紧迫时段。以90%置信区间为例，08：00—10：15下爬坡需求较其他时刻普遍增长300 MW 以上，18：30—20：30 较其他时刻普遍增长100 MW 以上，15：45—17：00上爬坡需求较其他时刻普遍增长200 MW以上。

5 结论

通过本文的研究可以得到以下结论。

1） 由于净负荷预测误差与预测值的相关性随时间变化具有较大差异，基于动态Copula函数的条件概率模型对于净负荷不确定性的刻画更为准确。

2） 净负荷正负预测误差与预测值的相依关系差异较大，应区分不同方向的爬坡需求分别进行测算。

3） 应用本文所提出的方法，测算得到的爬坡容量需求结果可以为爬坡紧迫时段的确定提供有效参考，有助于在日前阶段合理安排机组组合计划以满足系统实时可能出现的高爬坡需求；此外，在爬坡市场优化出清过程中需要权衡获取额外爬坡能力所需成本并避免因爬坡能力不足而导致的惩罚价格，应用测算得到的爬坡容量需求概率估计结果可为爬坡市场中爬坡产品需求曲线的形成提供量化分析依据。