基于负荷转移的售电公司分时电价优化策略

蔡湛，李泽文，邹睿奇，李浩，万重山

（长沙理工大学电气与信息工程学院，长沙 410114）

0 引言

随着电力市场改革的日益深化，以往垂直一体化的垄断市场被新增的市场主体打破，传统的电价机制改革也面临着新的挑战。随着2021年10月《关于进一步深化燃煤发电上网电价市场化改革的通知》的发布［1］，电力市场将进一步开放，这一电价新政将推动所有工商业用户全部进入市场并要加快落实峰谷分时电价政策、建立峰谷分时电价机制。在电力需求侧发展方面，随着数字化信息化时代的到来，电力系统朝着自动化、智能化的方向飞速发展，过去以行政手段为主的计划用电模式已经不能够满足需求侧管理的要求，而以经济手段为主的市场化调节机制将会成为未来需求侧管理的主要模式。售电公司作为电力市场的重要成员，承担了从电能市场购电、零售市场售电的重要角色，如何采取有效的需求侧管理服务手段引导电力用户积极参与电力市场交易是其当前亟待解决的问题［2-4］。

目前有关电力市场需求侧管理及售电公司的研究主要集中在以下几个方面：考虑需求侧管理的售电公司决策优化研究［5-7］，电力市场进一步开放对需求侧管理的影响［8-12］，微电网中需求侧管理资源的应用以及对应的新能源消纳方法研究［13-17］。当前售电公司需求侧管理的手段主要是实行峰谷分时电价套餐，通过分时电价引导用户合理用电。对于峰谷分时电价的研究主要集中在以下方面：考虑发电成本的发电侧峰谷分时电价研究［18］，发、售电侧联合的峰谷分时电价研究［19］，考虑用户响应的售电侧峰谷分时电价研究［20-25］。其中考虑用户响应的售电侧峰谷分时电价是峰谷分时电价的研究重点，通常采用需求价格弹性模型和负荷响应曲线这两种方法对用户响应进行分析。文献［20］从总体价格弹性、时间-价格弹性的角度建立了用户的反映度模型，并用充盈度和舒适度等指标反映用户的满意度，从而建立了基于用户响应并考虑用户满意度的分时电价决策模型。文献［21］通过需求价格弹性分析电价变化对用户的用电量的影响，并建立了以峰谷差最小为目标的分时电价用户响应模型。文献［22］通过分析用户消费心理与电价均衡之间的关系，建立了基于用户需求弹性的峰谷分时电价决策模型。文献［23］在分析电力负荷特性的基础上构建了反映负荷用电特性的用户负荷特征量，并获得了实施分时电价后用户的需求响应负荷曲线。文献［24］建立了基于用户需求响应的负荷优化响应模型，并给出了峰谷分时电价下用户需求响应活动优化方程的求解方法。文献［25］建立的用户负荷响应度曲线模型能够反映用户响应特性，并利用加权最小二乘法实现了模型参数校正，对不同的用户制定了峰谷分时电价的实时仿真流程。上述文献表明，针对峰谷分时电价的研究已经取得较大的进展，但现有的研究中售电公司利用分时电价来开展需求侧管理服务时，对用户的成本及收益考虑较少。

本文在分析湖南省钢铁、电石等高能耗工业用户用电特性的基础上，综合考虑了售电公司、工业用户成本及收益，构建了工业用户负荷转移成本模型，提出了售电公司峰谷分时电价双层优化模型，并利用Karush-Kuhn-Tucker （KKT）最优条件进行模型求解得到最优分时电价，对钢铁、电石等高能耗工业用户的仿真测算结果说明本文方法的有效性。

1 湖南省高能耗工业用电特性分析

1.1 湖南省高能耗工业用电现状

近年来，湖南省经济快速发展，社会用电量也飞速增加。2020 年湖南省社会用电量为192.928 TWh，同比增长3.5%，其中第一产业用电量1.75 TWh，同比增长5.7%，第二产业用电量103.039 TWh，同比增长4.3%，第三产业用电量34.896 TWh，同比下降0.5%。第二产业中，工业用电量从2015 年的86.696 TWh 上升到100.294 TWh。用电量的增长主要集中在第二产业，特别是高能耗工业用电，其中钢铁、电石等行业的用电量增长尤为突出。

高能耗工业用户是电力市场中最大、最重要，也是最直接的用户。高能耗工业的发展对地区电网负荷平衡有着深刻的影响，而其用电趋势又与地区的电价销售政策紧密相关，因此，制定科学、合理的电价政策以及研究电价对高能耗用户用电的影响是至关重要的。

1.2 钢铁、电石行业用电特性分析

钢铁行业是高能耗用电领域的典型代表。目前钢铁行业所处的环境已大不如前，“节能与环保”是当今的主题，许多企业已经是微利或者亏损的状态，合理利用资源关乎到钢铁企业的生存发展，因此对其开展需求侧管理服务迫在眉睫。钢铁行业的用电特性明显，主要有以下几方面：用电量大，其用电量在整个地区电网供电量中所占的比重大，如湖南某钢铁公司2020年的用电量为2.684 TWh，占地区电网供电量的28%；用电波动大，钢铁企业由于生产设备和工艺流程的需要，存在部分较大的冲击负荷，易引起电网运行波动；负荷曲线与生产状况直接相关，其负荷变化主要由设备运行状态、生产过程决定。

以湖南某钢铁公司为例，该公司的日用电负荷最大可达到211.200 MW，其日负荷曲线如图1 所示。由图1 可知，该公司在08：00、15：00、16：00以及23：00 的用电负荷大，处于高峰时期，00：00时、06：00 时、07：00、09：00、12：00、17：00 时以及22：00 时用电负荷小，处于低谷时期，峰谷差最大达到123.2 MW，其余时段用电则较为平稳。该公司用电量大，用电成本高，其负荷曲线主要由生产状况、生产过程决定，负荷波动大。

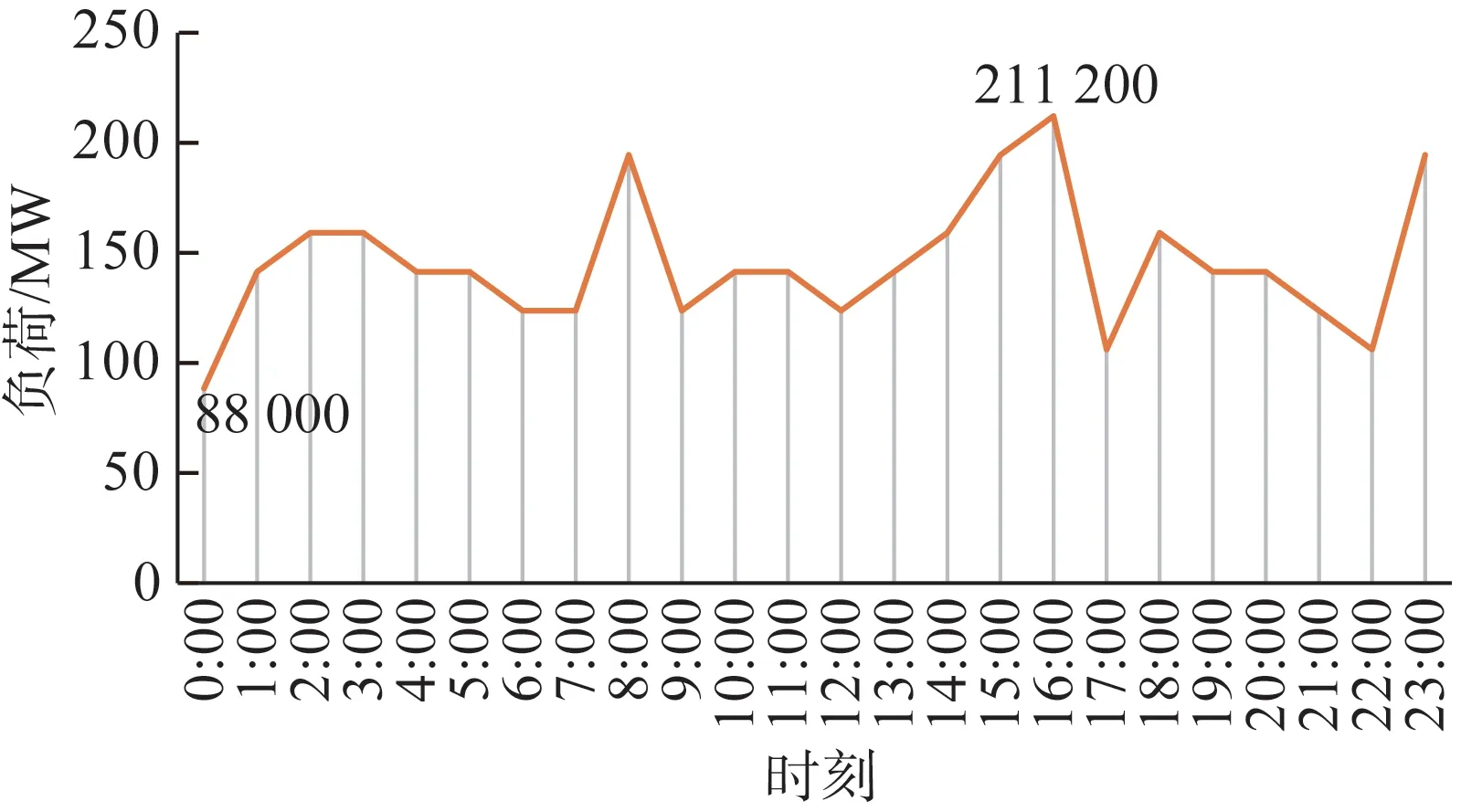
图1 钢铁公司日负荷曲线Fig.1 Daily load curve of steel company

电石即碳化钙，其工业生产的主要原料是焦炭和石灰石，属于高能耗产品。电石生产的过程中能耗高，其生产成本主要由电费、水耗、设备检修、员工工资以及蓝炭和石灰石等原材料成本构成，电费在这其中要占到70%左右，其用电量大，对电价变化的敏感程度很高。

以湖南某公司生产电石为例，该公司电石生产的日用电负荷最大可达71.340 MW，其日负荷曲线如图2 所示。由图2 可知，该公司电石生产用电高峰时期主要是在09：00—12：00、17：00—20：00，而05：00、13：00—14：00、21：00—23：00 用电负荷较小，处于低谷时期，峰谷差最大达到34.47 MW，负荷波动较大。

图2 电石生产日负荷曲线Fig.2 Daily load curve of calcium carbide production

通过对钢铁行业用户、电石生产行业用户用电特性的分析可知，若高能耗工业用户能根据电价政策适当调整生产安排，调整用电习惯，就能够有效节省用电成本，增加收益。

2 售电公司分时电价双层优化模型研究

通过对钢铁、电石等高能耗工业用户用电特性分析可知，售电公司实行峰谷分时电价能够引导他们合理用电，使双方获益。其中合理分配峰谷分时电价套餐参与双方的利益是售电公司开展需求侧管理服务的关键，因此，制定科学、合理的峰谷分时电价套餐是至关重要的。

2.1 售电公司成本收益分析

售电公司的成本主要指的是其购电成本，售电公司在购电时会和发电企业或者电网公司签订购电合同，合同中约定好购电量和购电价格，其购电成本可表示为：

式中：Tb为售电公司购电成本；Pe为购电价格；Qe为售电公司购买的电量。

售电公司的收益指的是销售电能给用户所得的收益。在实行峰谷分时电价套餐前，售电公司的售电价格与用户是统一约定好的，其销售每单位电能产生的收益就是售电价格与购电价格之差。实行峰谷分时电价套餐后，售电公司通过分时电价套餐内容向用户销售电能获取收益。峰谷分时电价实施前后售电公司的收益模型可分别表示如下。

式中：Pb、Pa分别为峰谷分时电价套餐实施前后售电公司的单位售电收入；Pf、Pp、Pg分别为峰谷分时电价套餐中峰、平、谷时段的电价；Qe，f、Qe，p、Qe，g为用户在一个负荷日内峰平谷各时段的用电量；Bs，0、Bs分别为售电公司在峰谷分时电价套餐实施前、后一个负荷日的收益。

2.2 工业用户负荷转移成本分析

峰谷分时电价套餐实行后，工业用户在确保自身利益的情况下极有可能会调整其能耗高的生产任务的工作时间来进行响应，以节省用电成本，其用电习惯及生产安排会发生改变，在高能耗的工序、生产任务的调整过程中也会产生相应的成本。

工业用户在用电高峰期转移其用电负荷所产生的成本，可以用可中断负荷合同中约定的补偿价格进行量化。可中断负荷合同是售电公司在电网负荷高峰时段或紧急情况下与用户所签订的合同，用户依照合同中断或削减负荷能够得到售电公司一定的经济补偿。用户中断或削减负荷亦是其生产安排的改变，且所得的经济补偿是用户在考虑自身利益情况下与售电公司竞价而来的，因此可以利用该补偿费用来反映用户因调整生产安排而产生的真实成本。进一步分析工业用户得到的经济补偿额度后发现，用户在用电的高峰时段所转移的电量越多，则每千瓦时可中断负荷的经济补偿费用（即负荷转移成本）越多；而用户在平谷时段基本不会抑制或削减自身用电量，此时的负荷转移成本可视为零。基于以上分析，建立的工业用户负荷转移成本模型如下所示。

式中：Tu为工业用户的负荷转移成本；i为时段，I为总时段数量，取24；Tu，i为第i时段工业用户的负荷转移成本；αi为工业用户负荷转移成本调整参数，根据可中断负荷的补偿价格给出；Qi，0为第i时段工业用户的正常生产安排所需的用电量；Qi为第i时段工业用户的实际用电量。

2.3 售电公司分时电价双层优化模型

售电公司在做出实行峰谷分时电价套餐的决策时，工业用户往往会根据自身条件做出合理响应，在售电公司确定峰谷分时电价套餐内容后，工业用户会根据该套餐内容调整自身生产安排，这个过程可以用双层规划数学模型来描述。在构建的双层优化模型中，上层模型针对的是售电公司的售电收益，其目标为实现售电收益最大化；下层模型针对的是工业用户的用电成本，其目标为使用电成本降低至最小。

售电公司分时电价双层优化模型基于以下假设。

1） 工业用户生产任务多，日常用电比较稳定，其正常生产安排调度不会因分时电价套餐发生重大改变，故可以假设实行峰谷分时电价套餐后工业用户的用电量仅发生转移而没有削减，日用电量没有发生改变。

2） 峰平谷时段的划分选用湖南省最新公布的工业用户分时电价时段：峰时段，11：00—14：00、18：00—23：00；平时段，07：00—11：00、14：00—18：00；谷时段，23：00—07：00。

3）峰谷分时电价中平时段电价与用户的用电水平紧密相关，而工业用户的用电水平在分时电价实施前后不会发生明显变化，故取平时段电价Pp与分时电价实施前的售电公司单位售电收入Pb相等。

2.3.1 上层优化模型

1）目标函数

上层优化模型针对的是售电公司的售电收益，其售电收益B指的是在实行峰谷分时电价套餐后向工业用户销售电能而产生的收益，其目标函数maxB为：

2）约束条件

售电公司的收益Bs在峰谷分时电价套餐实行后应当有所增加，故存在式（9）所示约束。

根据湖南省发改委最新公布的分时电价政策，峰谷电价应满足式（10）所示约束。

2.3.2 下层优化模型

1）目标函数

下层模型针对的是工业用户的用电成本，峰谷分时电价套餐实行后，工业用户的用电成本T主要为购电成本和负荷转移成本，因此，其目标函数minT为：

式中：Pi为工业用户在i时段购买电能的价格；Qi为第i时段工业用户实际用电量；Qi，0为第i时段工业用户正常生产安排所需用电量。

Pi可表示为：

2）约束条件

式中βi为工业用户的电量转移系数。

售电公司销售给工业用户的电量与工业用户总的用电量应当相等，故有式（18）所示约束。

3 分时电价双层优化模型求解

本文利用KKT 最优条件以及MATLAB 下的YALMIP 工具箱和CPLEX 求解器对该双层优化模型进行求解。

先假设峰谷分时电价套餐各时段的电价Pi已知，通过KKT 最优条件，求取工业用户合理响应分时电价套餐后的最优用电量Q*i，从而实现对下层优化模型的求解，具体的求解过程如下。

用KKT 最优条件求解工业用户最优用电量的标准型表示如下。

下层模型最优解的KKT条件为：

再将下层优化模型的最优解（工业用户的最优用电量）当作计算参数代入到上层优化模型中，将该双层优化模型求解问题转化为式（27）所示的单一的混合整数非线性问题。

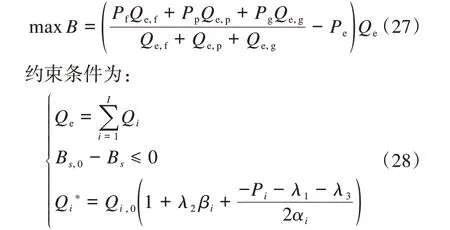
最后利用YALMIP 工具箱和CPLEX 求解器对上式进行求解，得到优化后的售电公司峰谷分时电价以及用户的用电量，整个求解过程的流程如图3所示。

图3 模型求解流程图Fig.3 Model solution flowchart

4 算例分析

4.1 原始数据与参数

湖南某售电公司售电业务广，售电量大，公司的钢铁、电石等高能耗工业用户众多，用户用电量大。公司的购电价格为0.355 0 元/kWh，钢铁、电石等高能耗工业用户的电压等级主要为10 kV、110 kV、220 kV，公司10 kV、110 kV、220 kV 工业用户的销售电价分别为：0.643 7 元/kWh、0.586 7元/kWh、0.562 7元/kWh。钢铁、电石高能耗工业用户的典型负荷日各时段用电情况如表1所示。

表1 典型负荷日用电情况表Tab.1 Daily electricity consumption table of typical load day MWh

由表1 可知，钢铁、电石等高能耗工业用户单位时段最大用电量为757.793 0 MWh，最小用电量为514.423 8 MWh。高能耗工业用户负荷转移成本的调整参数αi随时间变化关系如图4 所示，工业用户的电量转移系数βi取0.1。

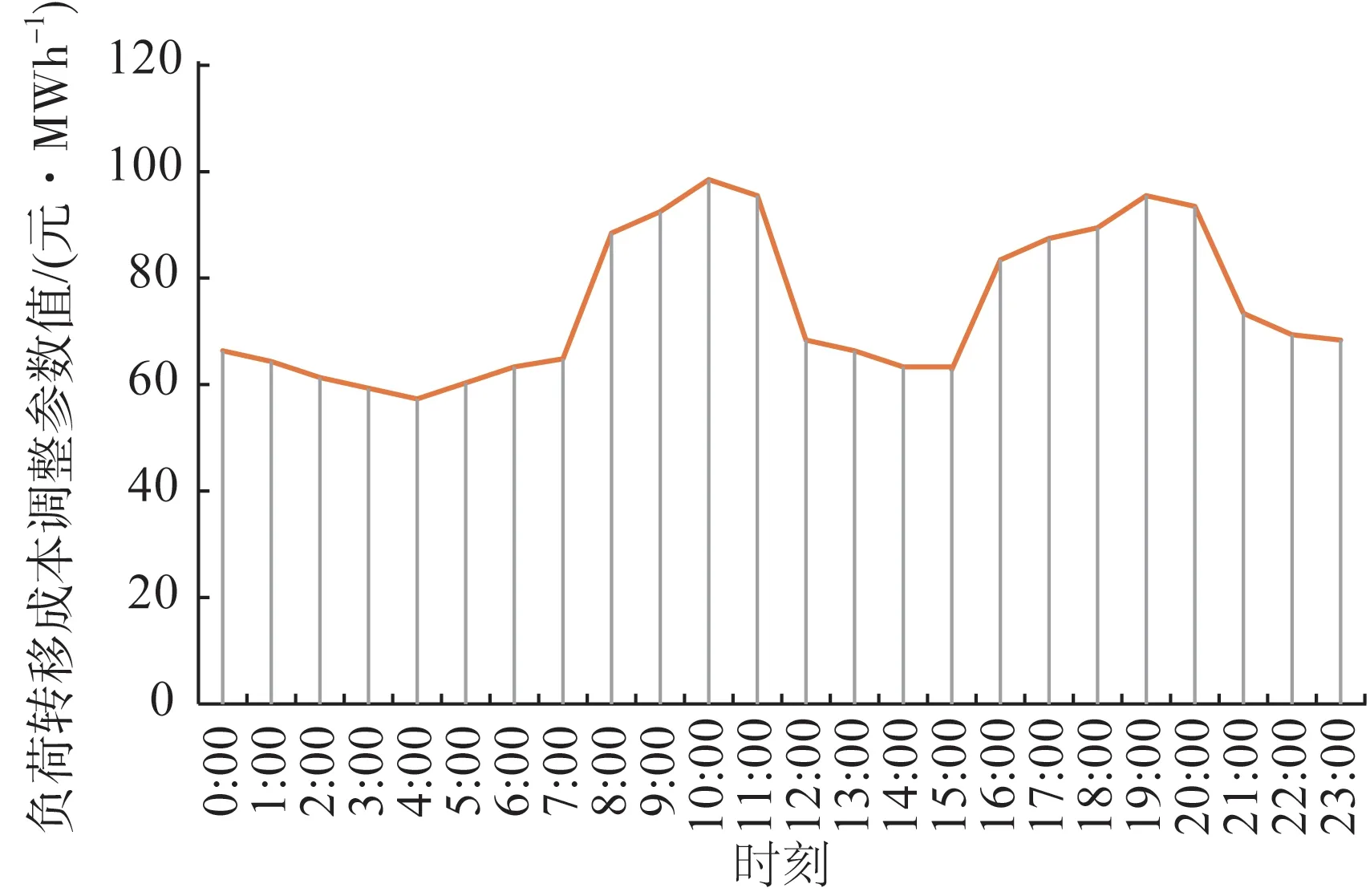
图4 不同时段工业用户负荷转移成本调整参数值Fig.4 The values of the load transfer cost adjustment parameters for industrial users at different times

4.2 结果分析

采用以上数据及所建立模型，调用MATLAB下的YALMIP 工具箱和CPLEX 求解器依次对10 kV、110 kV、220 kV 不同电压等级的高能耗工业用户进行模型求解，求得最优分时电价如表2所示。

表2 用户最优分时电价表Tab.2 User optimal time-of-use electricity price table元/kWh

优化前后高能耗工业用户的用电情况对比以及峰平谷各时段的用电量对比分别如图5、表3所示。

表3 峰平谷时段用电量对比Tab.3 Comparison of electricity consumption during peak and valley periods GWh

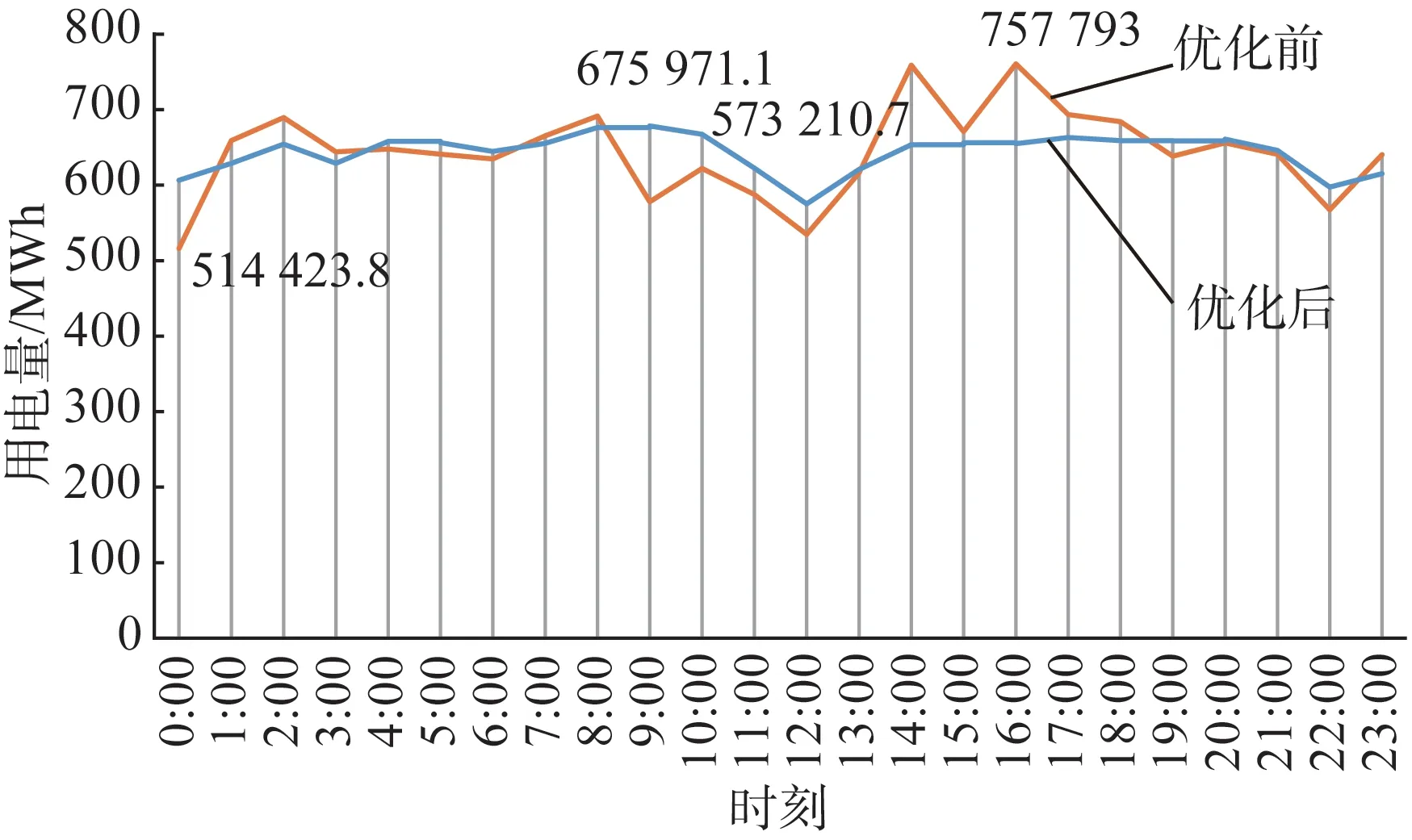
图5 电价优化前后用电情况对比Fig.5 Comparison of electricity consumption before and after the optimization of electricity prices

分析图5 可知，在实行表2 所示的峰谷分时电价后工业用户用电曲线变得更加平缓，最大用电量由757.793 MWh 降至675.971 1 MWh，最小用电量由514.423 8 MWh 增加至573.210 7 MWh，峰谷差由优化前的243.369 2 MWh 降至102.760 4 MWh，由此可见，实行该峰谷分时电价套餐能够达到削峰填谷的效果。

表3 数据表明，实行峰谷分时电价后平段与低谷时期的用电量明显增加，由表中数据进一步可求得售电公司与高能耗工业用户在峰谷分时电价实施前后的成本收益变化，如表4所示。

表4 优化前后双方成本收益对比Tab.4 Optimize the cost-benefit comparison between the two sides before and after 万元

分析表4 的数据可知，实施峰谷分时电价后售电公司一个负荷日的利润由339.102 96 万元增至339.640 88 万元，增加了5 379.2 元，高能耗工业用户在分时电价的调节下，一个负荷日的总用电成本由885.329 39 万元增至886.208 93 万元，增加了8 795.4 元，其中在调整生产的过程中产生了3 416.2 元的负荷转移成本，虽然其总成本有所增加，但增加的量是对数量众多的工业用户而言的，平均到每一用户的成本微乎其微，此外，高能耗工业用户的合理安排生产任务可以减少生产工人的倒班时间、提高工作效率，其产生的效益也会更大。由此可见，实行该峰谷分时电价套餐不仅能够保证售电公司和高能耗工业用户的利益，还能够引导用户合理用电，削峰填谷，减少电力资源浪费，提高用电负荷率。

5 结语

本文在分析湖南省钢铁、电石等高能耗工业用户用电特性的基础上提出了一种基于工业用户负荷转移的售电公司分时电价定价方法，所构建的分时电价双层优化模型充分考虑了售电公司、工业用户的成本收益，并利用KKT 最优条件实现了模型求解，以钢铁、电石等高能耗工业用户数据为例的仿真测算结果表明由模型确定的峰谷分时电价套餐能够在保证售电公司和高能耗工业用户的利益的同时引导用户合理用电、削峰填谷，同时，本文研究成果可为售电公司在电价新政背景下开展需求侧管理服务提供参考。