基于状态重构准谐振扩张状态观测器的LCL型并网逆变器电流控制策略研究
2024-03-05方健李辉
方健,李辉
(上海电力大学自动化工程学院,上海市 杨浦区 200090)
0 引言
并网逆变器是分布式发电系统与电网连接的重要接口,具有快速实现能量转换的优点,被广泛应用在并网系统中[1]。为了在高频段获得较好的谐波衰减能力,电网与并网逆变器之间一般采用LCL型滤波器。然而,LCL型滤波器是一个欠阻尼三阶系统,容易引起系统谐振,给并网电流控制带来困难[2-5]。抑制LCL型滤波器谐振的方法主要是增大系统阻尼,常用的方法有无源阻尼和有源阻尼2种。无源阻尼方法通过在滤波器元件上串入或者并入电阻,提高系统阻尼从而抑制谐振[6]。无源阻尼方法鲁棒性较强,但是由于增加电阻会带来额外的功率损耗问题。与无源阻尼相比,有源阻尼可以在不造成额外功率损耗的情况下达到相同的谐振抑制效果,因此得到更广泛的研究。有源阻尼大多数采用状态变量反馈法,如单状态变量反馈[7-9]、多状态变量反馈[10]、全状态变量反馈等[11]。几种状态变量反馈当中,电容电流有源阻尼由于其反馈系数为常系数,得到了更广泛的应用,但需要高精度电容电流传感器。多状态变量反馈及全状态变量反馈所需传感器数量更多,从而增加了系统的复杂性和成本,同时也可能因传感器故障而影响系统可靠性。
实现起来较为方便的滤波电容电流有源阻尼内环和并网电流控制外环至少需要3个传感器,其中2个电流传感器分别检测电容电流和网侧电感电流,电压传感器检测电网电压实现并网电流相位同步,但应用较多传感器会增加系统成本[12]。近年来,越来越多的研究转向基于观测器控制。通过观测器观测某个状态量,如电网电压[13]或者电容电流[14]等,但能够减少传感器数量十分有限。
并网逆变器的并网电流控制常规方法是在dq旋转坐标系下设计PI控制实现无静差跟踪。但该方法会面临着dq轴强耦合问题,需要设计相应的解耦策略[15]。自抗扰控制(active disturbance rejection controller,ADRC)不依赖精确数学模型,将系统异于积分器串联型的部分作为总扰动进行实时观测和补偿,对参数变化、噪声和干扰具有很强的鲁棒性[16-18]。并且ADRC具有天然的解耦能力,可将dq轴之间的耦合动态作为总扰动当中的一部分进行实时观测和补偿。
针对以上问题,本文采用一种基于状态重构准谐振扩张状态观测器(quasi resonant-extended state observer,QR-ESO)的LCL型并网逆变器电流控制策略,只需要一个逆变器侧电感电流传感器即可实现所需变量的全状态实时观测。针对在dq轴坐标系下的并网电流控制存在强耦合问题,设计了将耦合动态作为总扰动当中一部分的ADRC电流控制器,简化了传统电流控制当中复杂的解耦过程,同时也考虑了系统在受到各种扰动情况下状态重构QR-ESO的准确性。仿真结果表明,即使在参数摄动和电网电压波动的情况下,本文采用的方法依然具有较强的鲁棒性。
1 系统特性分析
三相LCL型并网逆变器系统结构如图1所示,其中,uv为逆变器输出电压;Li和iv分别为逆变器侧电感和电流;Lg和ig分别为网侧电感和电流;C和ic分别为滤波电容和电流;ug为电网电压;Udc为直流母线电压。

图1 三相LCL型并网逆变器系统结构Fig.1 Structure of three-phase LCL-type grid-connected inverter system
由图1可求得逆变器输出电压uv至网侧电流ig的传递函数为
根据式(1),其传递函数分母缺乏二阶项,根据Hurwitz判据可知,系统处于一种临界稳定状态,将导致系统产生谐振。因此,在设计并网电流控制器之前,首先需要考虑如何解决系统谐振问题。同时,为了实现并网电流控制,常规设计思路大多数采用在dq轴旋转坐标系下设计电流控制器,LCL型并网逆变器在dq轴坐标系下的数学模型为:
式中:ω为电网频率;ucd,ucq分别为电容电压的d,q轴分量。
根据式(2),在dq坐标系下,LCL型并网逆变器是一个多变量、强耦合系统,因此,设计解耦效果好的控制器尤为关键。
2 状态重构QR-ESO的电流控制策略
2.1 控制策略
本文提出的基于状态重构QR-ESO的电流控制策略如图2所示。主要包括逆变器侧电感电流状态重构、QR-ESO实时观测、状态转换、基于观测的并网电流控制及滤波电容电流的有源阻尼设计。该控制策略只需要一个逆变器侧电感电流传感器即可实现对所需状态变量的实时观测,减少了电网电压传感器及电容电流传感器的使用。
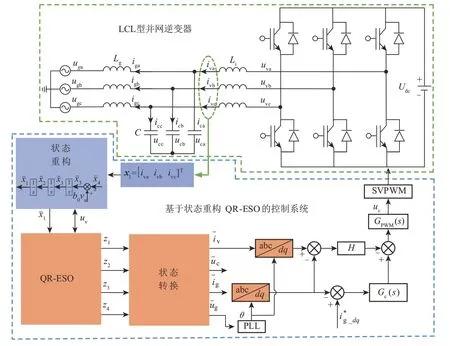
图2 基于状态重构QR-ESO的电流控制策略Fig.2 Current control of GCI based on state reconfiguration with QR-ESO
根据图2,系统整体控制策略的流程步骤如图3所示。首先,利用电流传感器实时检测逆变器侧电感电流的值;其次,结合LCL滤波器满足的基尔霍夫电压电流方程对逆变器侧电感电流进行状态重构,使新构建的状态变量满足积分器串联形式;然后,通过QR-ESO对新构建的状态变量进行实时观测,并将QR-ESO的观测输出进行状态转换,依次得到iv、uc、ig及ug的观测值;最后,利用QR-ESO观测的电网电压进行锁相,在dq轴旋转坐标系下分别设计ADRC实现并网电流跟踪。根据QR-ESO观测的网侧电流ig与逆变器侧电流iv相减并进行常系数反馈实现有源阻尼。这2部分产生的控制量经过处理后形成并网逆变器控制调制波,将该并网逆变器控制调制波送入空间矢量脉宽调制(space vector pulse width modulation,SVPWM)模块后得到驱动开关器件脉宽调制信号。

图3 控制策略流程图Fig.3 Flow diagram of control strategy
本文所提控制策略当中ADRC与QR-ESO是相互独立的2个模块,所起的作用也不相同。其中,QR-ESO主要是作为观测器使用,获得所需状态变量的实时观测值。QR-ESO借用了ADRC当中ESO的概念,并做了适当的改进,用来更好地观测交流信号。而ADRC在本文所提控制策略当中作为电流控制器使用,为图2中的Gc(s),主要用来处理电流控制在dq轴坐标系下的耦合问题以及各种不确定因素对系统的影响。
2.2 逆变器侧电流状态重构
根据图1所示的LCL型并网逆变器结构,得到LCL滤波器满足的基尔霍夫电压电流方程为:
根据(3)可以看出,状态变量ig、iv、uc的状态方程之间存在一定量的耦合关系,并且uv和ug也出现在方程当中。所需状态变量有ug、ic和ig,ic可以通过ig和iv相减获得。因此,如果可以设计出能同时观测出iv、ig和ug的观测器就可以最大程度减少传感器数量。
本文所提控制策略,旨在通过ESO观测所需状态变量。ESO的基本结构是内部状态变量呈现积分器串联形式,而式(3)中的状态变量显然不满足该形式。如若需要通过ESO观测出所需状态变量,则需要构建一组即满足积分器串联形式,同时包含式(3)所涉及的状态变量。不妨令:
将式(4)代入式(3)可得:
进一步地,对iv进行状态重构,即对逆变器侧电流分别进行3次微分运算,使得新构建的状态变量满足积分器串联形式,如式(6)所示:
2.3 QR-ESO全状态观测及状态转换
根据式(6)所新构建的状态变量,设计相应的ESO进行实时观测,如式(8)所示:
由于ESO内部是几个积分器串联的形式,纯积分器在零频率的增益是无穷大的。因此,ESO大多数是用来观测直流或者较为低频的量。新构建的状态变量都属于50 Hz的交流信号,ESO需要增加观测器增益来改善观测精度,但同时也会引入高频噪声至控制回路。通过在ESO每个状态变量的观测通道添加准谐振环节,并将谐振频率设定在50 Hz处,则能够在50 Hz提供较大的观测增益,大幅度改善对逆变器正弦信号的观测精度。准谐振传递函数如(9)所示,QR-ESO的内部结构如图4所示。

图4 QR-ESO内部结构Fig.4 Internal structure of QR-ESO
式中:ωg为电网频率;T1、T2为常系数,且T1>T2。
QR-ESO的观测输出并不是所需要的状态量,但可以根据式(6)和(7)进行状态转换,依次得到iv、uc、ig和ug的实时观测值,如式(10)所示:
2.4 ADRC电流控制器
通过式(2)可以看出,由于采用的是LCL型滤波器,在dq轴旋转坐标系下的耦合现象会比采用L型滤波器更为严重,所以设计一个解耦效果好的控制器尤为关键。
ADRC具有天然的解耦能力,可将耦合项作为总扰动当中的一部分,并利用ESO进行实时观测和补偿。由于系统为三阶的,而常规ESO的设计则为四阶,阶数越高,观测总扰动的相位滞后也越大,这将降低系统观测的快速性,并且会减小系统的稳定裕度。通过将输出y的高阶导数作为总扰动当中一部分,设计一阶ADRC电流控制器,如图5所示,从而简化了设计过程和参数整定。

图5 低阶ADRC电流控制Fig.5 Low-order ADRC current controller structure
根据式(2)当中网侧电感电流与逆变器侧电压的关系,令y=ig_dq,u=uv_dq,可得到式(11),由于dq轴具有对称性,后面都以d轴为例。
从ADRC的角度来看,所有不同于积分器串联型的动力学都可以看作是总扰动,然后利用ESO进行实时观测和补偿。令:
则式(11)可以改写为
式中b=1/Li。
因此,二阶ESO可以设计为
式中:̂分别为状态变量̂的实时估计;β1,β2为观测器增益,利用极点配置方法将观测器极点都配置在处。
在合理设计观测器的前提下,设计如下控制律,实现对总扰动的实时补偿:
式中:r为dq轴网侧电流参考信号;kp为控制器增益。将式(16)代入式(13),可得
因此,闭环系统传递函数可以等效为
显然,如果̂能很好地估计系统输出和总扰动,则可以通过设置kp来确定闭环系统的性能。令分别为观测器带宽和控制器带宽。
3 仿真与结果分析
为了验证所提出的基于状态重构QR-ESO的并网逆变器电流控制策略有效性,在PLECS软件平台上搭建了如图2所示的仿真模型。主电路参数见表1,控制器参数见表2。

表1 主电路参数Tab.1 Main circuit parameters

表2 控制器参数Tab.2 Controller parameters
1)仿真结果1
考虑在相同的观测器带宽,即ωo=2 000 rad/s时,基于状态重构ESO与状态重构QR-ESO对各个状态变量的观测效果如图6所示。从图6可以看出,在相同的观测器带宽的情况下,传统ESO存在较大的观测误差,而所提的QR-ESO能够较为精确地观测状态变量。

图6 ESO与QR-ESO的观测效果对比Fig.6 Comparison of ESO and QR-ESO observations
2)仿真结果2
考虑在参数摄动及电网电压波动情况下,验证本文提出的观测策略的准确性。分别让Li、Lg和C的值增加20%,以及在0.35 s时电网电压骤升30 V,此时系统的观测效果如图7所示。可以看出,在参数波动幅度比较大以及电网电压突变的情况下,本文提出的状态重构QR-ESO依然能够比较精确的观测状态变量。

图7 参数摄动及电网电压波动情况下的观测效果Fig.7 Observation effects under parameter perturbations and grid voltage fluctuations
根据式(10)可知,逆变器侧电流iv的观测值不受电感电容参数影响,所以在观测稳定的参数范围内无论如何改变电感电容值都不会影响iv的观测精度。电容电压uc的观测精度会受到电感Li的影响,由于Li取值比较小,所以导致Li∙z2很小,只有几伏左右,而uv的值约311 V,所以尽管Li参数变化过大,但对uc影响也较小。同理,经过定量分析,网侧电流iv的观测值和电网电压ug的观测值受参数摄动的影响也较小。
图8、9分别为电网电压存在谐波以及并网电流设定值存在谐波情况下各状态变量的观测效果,可以看出,即使存在谐波的情况下,本文所提的策略依然能够较好地观测各状态变量。
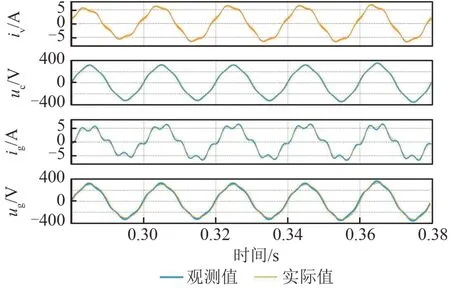
图8 电网电压存在谐波时的观测效果Fig.8 Observation effects in the presence of harmonics in the grid voltage
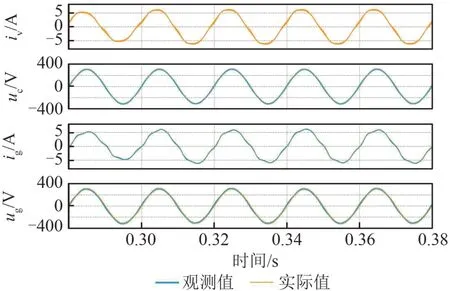
图9 并网电流存在谐波时的观测效果Fig.9 Observation effects in the presence of harmonics in grid-side currents
3)仿真结果3
为了验证本文提出的ADRC电流控制器的解耦能力和抗干扰能力,该控制器与传统的PI控制器在系统相同带宽下进行了仿真对比,PI控制器的参数见表2。图10对比了在正常工况下2种控制方法的动态性能,可以看出,采用的ADRC相较于PI控制的超调量更小,调节时间更短。

图10 正常工况下的dq轴电流控制效果Fig.10 Effect of current control of dq frames under normal working conditions
考虑在0.35 s电网电压产生30 V的骤升,对比2种控制方法在存在外部干扰的情况下的动态性能,如图11所示。

图11 电网电压波动工况下的dq轴电流控制效果Fig.11 Effect of dq frames current control under grid voltage fluctuation conditions
从图11可以看出,在电压扰动的情况下,ADRC能够比PI控制更快地恢复到稳定状态,抗干扰能力及动态性能更好。
4)仿真结果4
为了分析系统在加入状态重构QR-ESO之后的动态性能与未加入之前的区别,分别绘制了2种情况下系统的开环和闭环Bode图,如图12、13所示。加入状态重构QR-ESO时系统的穿越频率在105 Hz,相位裕度为35°左右,系统是稳定的;而未加入状态重构QR-ESO时系统的穿越频率在131 Hz,相位裕度为38°左右。加入状态重构QRESO的并网逆变器系统相较于没加入之前的系统相位裕度损失一部分,这是由于观测器相当于一个低通滤波器,会增加系统相位滞后。
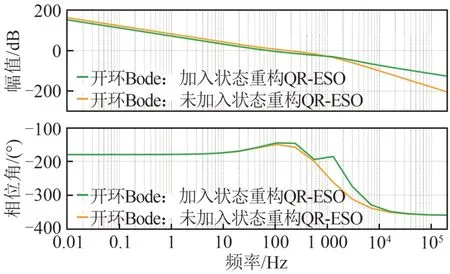
图12 系统开环Bode图对比Fig.12 Comparison of system open-loop Bode diagrams

图13 系统闭环Bode图对比Fig.13 Comparison of system closed-loop Bode diagrams
系统的闭环Bode图在低高频段几乎一致,在中频段有些区别,但系统的闭环带宽处于相同数量级。从系统的开闭环Bode图上可以看出,系统在加入状态重构QR-ESO与未加入之前的控制性能基本一致。
4 结论
针对三相LCL型并网逆变器的有源阻尼及并网电流控制需要多个传感器以及在dq轴坐标系下存在强耦合问题,提出了一种基于状态重构QRESO的全状态观测控制方案。通过仿真分析得出以下结论:
1)所提控制方案只需要一个逆变器侧电感电流传感器就可以实现对所需状态变量的实时观测,最大程度地减少了传感器的使用,降低了硬件成本。
2)QR-ESO相较于传统ESO在观测正弦交流量的情况下,观测效果更好,精度更高,解决了传统ESO跟踪正弦信号需要高观测器增益的问题。
3)采用的ADRC电流控制器相较于传统的PI控制器的解耦过程更加方便,效果更好。动态响应过程的超调量更小、调节时间更短,在电网电压波动情况下能够更快恢复至稳态。
