基于无电网电压传感器的Vienna整流器滑模模型预测控制
2024-03-05姜雅飞
姜雅飞, 赵 刚
(1. 江苏航运职业技术学院 海洋工程系, 江苏 南通 226010; 2. 西安交通大学 电力设备电气绝缘国家重点实验室, 陕西 西安 710048)
作为一种特殊的能量仅能单向流动的三电平整流装置,Vienna整流拓扑由于具有较高的能量密度、无需设置开关死区、并网电流谐波小、开关管电压应力低以及可靠性高等优点,在数据中心、航天电源、电机驱动以及车载电源等中小功率场合受到了国内外学者的广泛关注[1-3].目前关于Vienna整流拓扑的研究热点主要集中在如何提高并网电流质量、改善功率密度与实现中点电位平衡控制等方面.常规的控制策略主要分为直接电流控制、间接电流控制和功率控制[4-5].传统控制策略的输出性能强依赖于控制器参数且难以实现多目标跟踪.有限集模型预测控制(finite control set model predictive control,FCS-MPC)作为一种高效的多目标控制算法,可考虑多种约束条件,因此更适用于强非线性的三电平Vienna整流器控制系统[5-6].然而无论是采用传统的控制策略或模型预测控制,为达到控制目标需要采集电网电压的幅值、相位信息,在实际运用中可安装电网电压传感器以获得电网电压信息,但相应地会增加系统成本和硬件复杂度、降低系统可靠性,此外还存在噪声灵敏度高、分辨率受限等问题[7-8].因此,有关并网变换器无电网电压传感器的控制引起了国内外学者的广泛关注.
无电网电压传感器控制策略的基本思路是利用数学模型推算出的桥臂电压与交流侧滤波器压降之和来估算电网电压.由于该方案需对电流进行微分运算而导致噪声灵敏度高,相关学者相继提出了几种电压重构方式,如虚拟磁链[8]、滑模观测器[9]、自适应全阶观测器[10]等.其中虚拟磁链由于实现简单、观测效果较好,更适用于强非线性的三电平Vienna整流器.传统的磁链观测通过将源侧与虚拟交流电机进行等效处理,此时电网电压作为虚拟磁链的微分值,利用引入积分环节进而得到虚拟磁链.Tao等[11]提出带有初值估算的低通滤波器代替纯积分环节来估算磁链,从而达到降低冲击电流、提高系统动态性能的目的.罗德荣等[12]采用了基于反馈补偿的虚拟磁链观测方法用以消除积分环节的影响,但是其观测精度受限于反馈限幅器.此外,传统的磁链观测由于存在纯积分环节,带来了积分初值与直流偏置等问题.
基于此,本文提出了一种三相Vienna 整流器电网电压估算方法,利用二阶低通滤波器消除积分初值和直流偏置问题,从而提高观测精度;利用SMC外环计算有功功率的给定值,进一步采用模型预测直接功率控制(direct power mode predictive control with constant frequency,DPMPC-CF)与滑模(sliding-mode control,SMC)外环控制的的双闭环复合控制方法,以功率跟踪误差最小为目标得到三桥臂的开关序列,从而实现基于直接功率模型预测控制的无电网电压传感器控制策略;最后,从静态、暂态、调制信号等多个维度进行了验证分析,结果表明所提出的控制方式具有良好的稳态和动态性能.
1 Vienna整流器数学模型及DPC策略
本文研究对象的电路拓扑[13-14]如图1所示.其中:ua、ub和uc分别是三相输入电源,L是交流侧的滤波电感,R是线路的等效阻抗,C1和C2是直流侧容量相同的滤波电容,udc1和udc2分别表示直流侧两个滤波电容的端电压,R1和R2表示负载,Dxp、Dxn是二极管,Sxp、Sxn是两个反向串联的功率开关管,udc表示直流输出电压,up与un分别为直流侧正负母线电压.
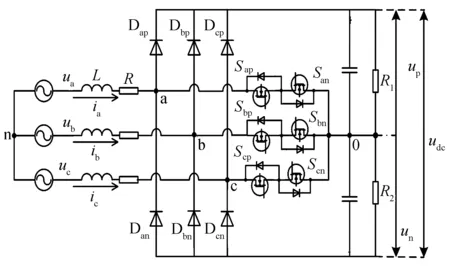
图1 三相三电平Vienna整流器的电路拓扑Fig.1 Circuit topology of three-level Vienna rectifier
本文根据图1所示的电路拓扑,列写电路状态表达方程为
(1)
式中:uxo为整流桥的输入端到交流侧中点的电位,uxo与开关状态之间的表达方程为
(2)
在式(1)中引入Park变换并离散化,则电路数学模型为
(3)
式中:k表示kTs时刻;k+1表示(k+1)Ts时刻;uα(k)与uβ(k)为电网电压在α-β坐标下的α、β分量.
根据瞬时功率理论计算系统的瞬时有功功率和无功功率表达式为
(4)
对于理想电网,在α-β坐标系下电网电压和电网频率之间满足以下关系:
(5)
因此,无功功率和有功功率的预测值可表示为
(6)
本文将功率误差的平方总和作为代价函数衡量指标,其对应的表达式为
g(i)=[p*-pp(k+1)]2+[q*-qp(k+1)]2
(7)
式(6,7)中:上标p表示预测值;*表示参考值.
2 电压外环SMC系统设计
Vienna整流器直流侧输出电压控制环路输出信号作为直接功率控制的给定信号,其性能直接会影响到系统的稳定性与可靠性.基于上述考虑,在此采用基于滑模算法的电压环路设计方案[15-16].从直流侧分析系统功率流动,列写直流侧电路方程为
(8)
忽略线路阻抗与开关损耗,则可列写如下表达方程:
(9)
将式(9)化简可得:
(10)
选取滑模面函数为
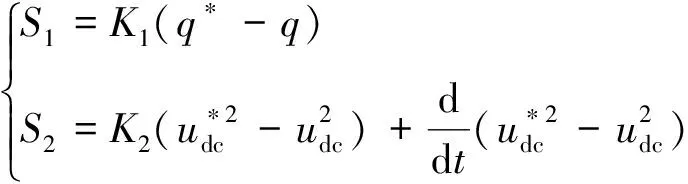
(11)
(12)
3 基于虚拟磁链的电网电压观测
根据式(1)可以得到Vienna整流器的电网电压估算方法,但由于需要引入电流微分计算,导致噪声敏感性高,因此在实际中较少采用.本文在此对式(1)引入坐标变换,并积分可得:
(13)

根据图2,电网电压矢量超前虚拟电网磁链矢量π/2,并结合图 2 中各变量矢量位置关系可以写出如下关系式:
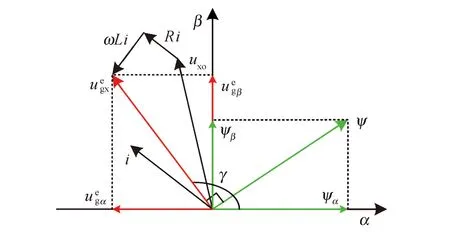
图2 α-β坐标系下Vienna整流器的矢量图Fig.2 Estimation strategy of power grid electromotive force vector
(14)
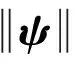
(15)
整理式(13,14)可得:
(16)
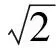
(17)
4 仿真验证分析
为验证本文理论分析的正确性与优越性,构建了完整的控制环路仿真模型与测试模型,并分别从静态响应、网侧电流THD和暂态响应几方面进行了验证分析.仿真中所涉及的主要参数见表1.在此需要指出的是,测试中的系统参数与仿真参数均保持一致,其中仿真步长为1×10-6s,Vienna整流器控制系统框图如图3所示.电压外环采用SMC控制器计算生成内环功率给定参考值,利用虚拟磁链观测实现对电网电压的无传感器观测,与瞬时功率比较后根据电压矢量扇区划分选择最优矢量,经PWM驱动开关管.
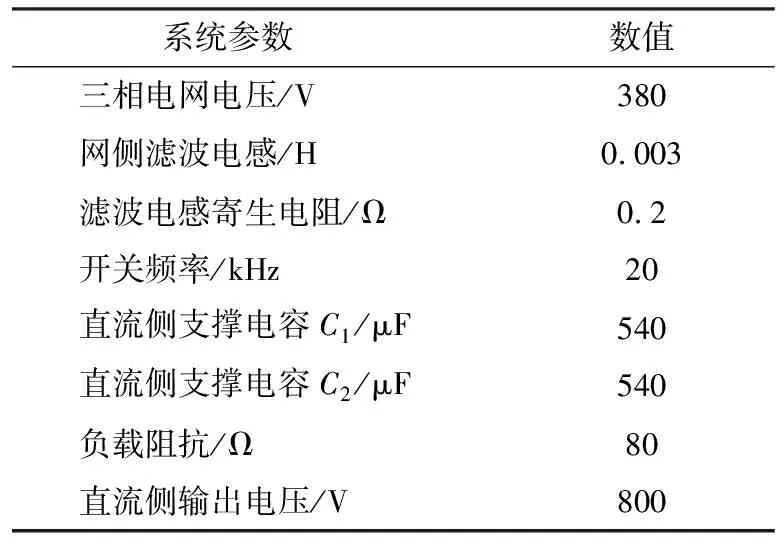
表1 系统的电路参数
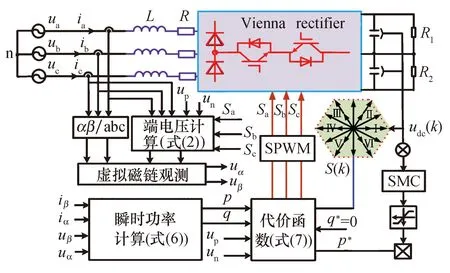
图3 控制原理框图
图4表示稳态时电网电压实际值与估计值的响应波形.显然,采用本文电压观测器可以实现快速跟踪电网电压变化,过渡时间约为0.005 s,验证了本文提出的电网电压观测方法的正确性和准确性.

图4 估计电压值和实际电压值Fig.4 Estimated value and actual value of grid voltage
图5与图6分别给出了在不同工况下的静态响应波形,满载下网侧电流THD为0.99%,半载模式下电流THD为2.67%,网侧电流纹波较大,电网电压与网侧电流始终保持同相位,满足国标要求.
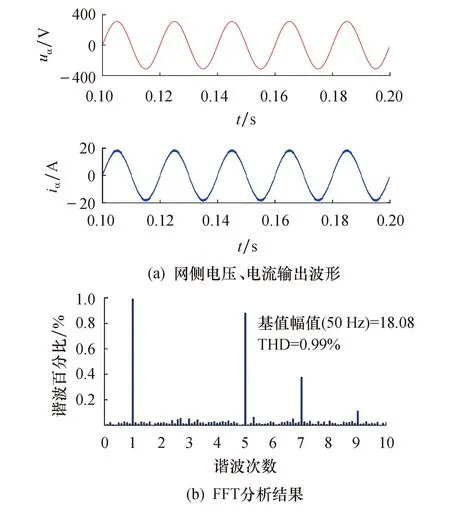
图5 满载工况下的静态响应波形

图6 半载工况下的响应波形Fig.6 Static response waveform of half load
图7为采用不同电压外环控制方式下的直流侧输出响应.由图7a可知,输出电压经半个周波后达到稳态,系统暂态响应良好.由图7b和图7a对比可以看到,不论采用滑模控制或是PI控制,直流侧输出电压均能稳定在800 V,但不同的是,PI控制下存在一定的稳态误差且电压纹波相较于滑模控制较大,在0.2 s切换至满负荷运行时,随着网侧电流的增大中点电位波动呈震荡增大.采用本文控制方式时,此时中点电位脉动仅为±0.1 V左右,当满负荷运行时,中点电位波动较小,同时可以看到网侧电流纹波也得到了显著抑制.

图7 暂态输出波形
图8为当直流侧电压给定分别在0.3 s与0.5 s由700 V阶跃变化至750 V和800 V时的动态响应波形,可以看到当直流侧电压给定突变时,系统能够实现快速跟踪.
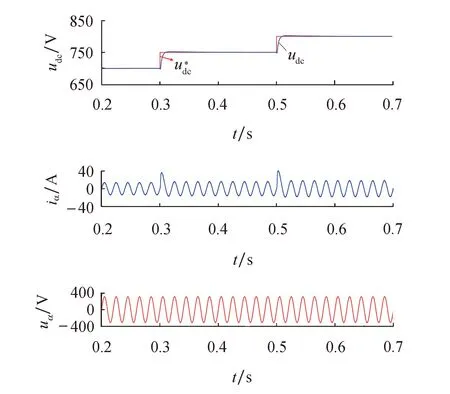
图8 电压给定突变情况下的响应波形Fig.8 Response waveform when the given voltage changed
5 实验结果分析
为了对本文所提DPMPC-CF的准确性进行验证,构建了基于RT-LAB半实物平台的Vienna电路验证模型,控制算法基于快速半实物模型RT-LAB实现.
在系统稳态工作时,图9给出了不同工况下的测试结果.从图中可以看出,网侧电流保持较好的正弦度且无明显畸变,直流电压稳定在800 V,且无电压波动,满载工况下THD=1.28%,降载运行下THD=2.84%,完全满足国标要求,实现了单位功率因数控制.
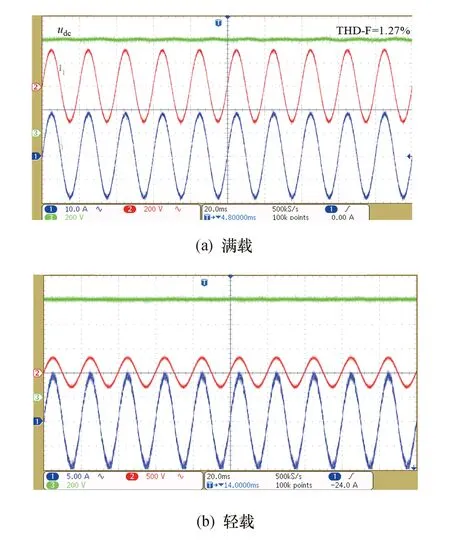
图9 静态输出响应Fig.9 Static output response
图10给出了当系统由满载切换至半载并由半载切换至满载运行时的暂态响应输出波形.可以看到,当系统负载突减,直流侧电压经过短暂的跌落最终回到给定输出,说明系统动态响应更快,可见系统动态性能良好,能有效抑制负载扰动.

图10 动态响应波形Fig.10 Transient response waveform
图11为当直流侧电压给定分别由700 V阶跃变化至750 V和800 V时的动态响应波形,系统能够实现快速跟踪,进一步表明了本文所提出的双闭环控制策略具有良好的动态性能.
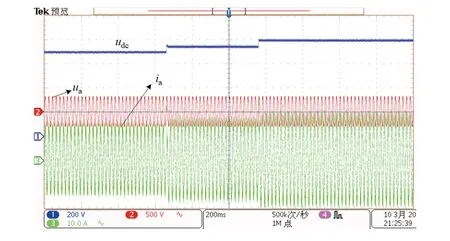
图11 直流电压给定变化时的响应波形Fig.11 Response with the change of DC voltage
6 结论
本文以三电平Vienna整流电路为研究对象,为改善传统控制方法依赖电网电压信息的缺点,提高电网电压观测精度和电流控制精度,提出一种基于磁链观测的无电网电压传感器的双闭环控制方法,并将滑模控制嵌入外环,形成滑模直接功率预测复合控制方法.与传统PI控制相比,该控制方法能够有效减小直流侧电压稳态误差;采用文中的观测方式可以实现电感电压的准确观测,不论是暂态或是静态电网电压观测效果良好.
