不同设计参数对液氧甲烷发动机喷管效率的影响

2024-03-05刘阳旻

导弹与航天运载技术 2024年1期

刘阳旻，田原

（北京航天动力研究所，北京，100076）

0 引言

火箭发动机中喷管的作用是将燃气的热能转化为动能，加速后的气流对喷管产生反作用推力。燃气在喷管内流动会有各种损失，其中以几何损失、附面层损失、化学动力损失为主。喷管效率为相同混合比、相同室压条件下的实际真空比冲与理想真空比冲之比。提高喷管效率是喷管设计的主题，曹彬彬等［1］使用CFD技术研究了不同设计参数对固液火箭发动机的喷管效率的影响；王长辉等［2］使用CFD 技术计算了不同设计对塞式喷管性能的影响；陈林泉等［3］使用类似于美国SPP［4］软件的方法研究了喷管扩张段型面对固体发动机的喷管效率的影响；Manski 等［5］使用TDK［6］研究了不同设计参数对氢氧发动机喷管效率的影响。而液氧甲烷发动机凭借着其优秀的经济性和可复用性得到了国内外广泛关注，但目前中国尚未针对液氧甲烷发动机设计参数对喷管效率影响进行过系统研究，故本文采用一种自研的高效二维喷管化学动力流场计算程序研究了液氧甲烷发动机不同设计参数对喷管效率的影响。

本文首先对推力室中各种损失的定义进行了介绍，随后简要介绍了自研程序的基本工作流程和方法原理，并给出针对SSME 喷管的计算结果，与文献［5］和［7］使用TDK 计算的结果进行了对比，结果基本一致，在此基础上对某液氧甲烷发动机喷管流场进行了仿真，研究了不同设计参数对喷管效率的影响，并且其计算速度极快，能够有效提高工程仿真效率。

1 火箭喷管效率定义

本文将喷管损失作为火箭设计参数的函数来进行研究。化学动力损失、几何损失及附面层损失［8］是研究的主题。

为了衡量化学动力损失，化学动力效率被定义为

比冲ISODE由一维平衡分析计算得出，比冲ISODK是由一维动力学流动分析计算得出。

为了衡量几何损失，几何效率ηISdiv被定义为

比冲IS2D使用包括化学动力效应的二维流动分析计算得出。

为了衡量附面层损失，附面层效率ηISfric被定义为

比冲ISBL使用包括化学动力效应、附面层及传热的二维流动分析计算得出。

喷管效率ηISnoz由下式得到：

随着外界气压的不同，计算的比冲值也会不同，而本文均使用真空比冲进行计算分析，而上述比冲的具体公式可参考文献［6］。

2 计算方法

本文使用自研程序进行计算，它是一款无黏流场结合附面层修正的二维喷管化学动力流场求解器，其中无黏主流部分使用特征线法［9］计算考虑化学反应的喷管流场，化学反应以有限速率模型建模，附面层修正部分采用的是T.Cebeci［10］的二维/轴对称可压缩附面层方程求解方法，并且附面层计算也考虑了化学效应，程序结构和计算框架示意见图1和图2。

图1 程序结构Fig.1 Program structure

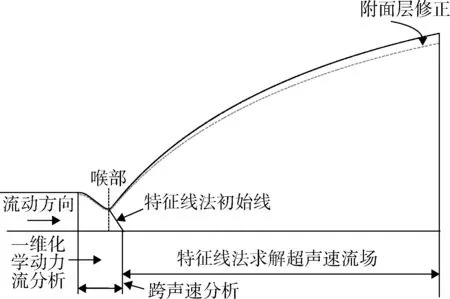
图2 程序计算框架示意Fig.2 Schematic for program analysis

程序基本流程是先进行一维平衡计算再进行一维非平衡计算，一维平衡计算主要使用的是最小吉布斯自由能法，其原理可参考美国CEA［11］软件，一维平衡计算得到的轴向压力分布和收敛段入口的燃气组份及物性参数将作为一维非平衡计算的输入，一维非平衡计算的方程为

马赫数大于1.04时，采用下述方程：

式中ci为i组分的浓度；ωi为i组分的净反应生成速率；Ri为i组分的气体常数；x为喷管轴向距离/喉部半径或者曲线坐标系流向坐标；r*为喉部半径；V为总速度；P为压强；ρ为密度；T为温度；γ为比热比；aˉ为喷管面积比；A为联系流动和化学反应过程的绝热额外项；B为联系流动和化学反应过程的能量交换项；hi为i组分的静焓；M为马赫数或者第三体。

单组分的净生成速率ωi使用有限速率模型建模求解，采用碳、氢、氧、氮11 组元（H、H2、H2O、OH、O、O2、CO、CO2、N、NO、N2），16步化学反应模型［7］：

这里M代表第3体，有限速率模型原理可参考文献［12］，一维非平衡求解方法可参考文献［7］和文献［13］。

喉部跨声速区的控制方程为

式中u'，v'为小扰动量。

利用改良的Sauer 方法对其进行求解，得到特征线法初始线，求解结果与参考文献［7］一致。

接着进行二维特征线法计算，由于特征线法只适用于双曲型方程的性质，故该模块只计算喷管扩张段流场，采用柱坐标系，求解的方程沿流线为

沿左特征线：

沿右特征线：

这里的A和B同前文。

式中r为从对称轴开始的径向距离/喉部半径；θ为轴向与径向速度夹角；α为马赫角；H为总焓。

使用特征线法具体的求解过程可参照文献［9］。

收缩段一维和扩张段二维非平衡计算的结果将作为附面层模块的输入进行附面层修正计算，附面层模块求解的是曲线坐标系下的轴对称可压缩薄边界层方程，如下：

式中u为轴向速度或者曲线坐标系流向速度；v为径向速度或者曲线坐标系纵向速度；y为曲线坐标系纵向坐标；cp为定压比热容；k为流动指标数，k=0时为二维流动，k=1 时为轴对称流动，雷诺应力使用C-S零方程模型建模，采用盒式格式差分求解，具体方法可参考文献［14］。附面层模块没有组分方程但是在物性设置上使用了近似化学平衡的物性插值方法，具体方法可参见文献［7］。

附面层模块只运行一次，其输出的位移厚度随后被向内叠加到原型面上，得到新型面，并将计算得到的再生冷却热增加到推进剂焓中（初始推进剂焓采用未吸收再生冷却热的值），然后再进行一次无黏计算，这便是本文所用程序的全部流程（不考虑传热时，可不进行二次无黏计算）。

图3 和图4 是使用自研程序对SSME 比冲、喷管效率、位移厚度分布及动量厚度分布计算的结果。图3中不同颜色的散点对应文献［5］中的结果。图4中实线为程序计算结果，散点为文献结果。

图3 SSME喷管比冲与喷管效率计算验证Fig.3 SSME nozzle specific impulse and nozzle efficiency calculation verification

图4 SSME喷管位移厚度与动量厚度分布计算验证Fig.4 SSME nozzle displacement thickness and momentum thickness distribution calculation verification

由图3 和图4 可知，本文所使用的的自研程序在SSME 喷管上的计算结果与Manski［5］使用TDK/BLM对SSME 喷管比冲与喷管效率计算的结果基本一致，数值上存在误差主要是由于程序差异，并且低室压时误差有所增加，原因可能为Manski 使用厚附面层方程组进行附面层修正计算，低室压时喷管附面层厚度增加，本文使用的附面层修正模块所采用的薄附面层假设适用性降低，但这并不影响后面对甲烷发动机进行性能分析，同时SSME标准工况下自研程序计算得到的位移厚度与动量厚度分布与Nickerson［6］使用TDK/MABL 得到的结果几乎完全一致，因此总的来说自研程序的计算结果与文献符合很好，程序正确性得到了验证。

为了研究设计参数对甲烷发动机喷管效率的影响，本文选择了室压、喉部半径、面积比和喷管出口角度作为自变量。本程序在喷管型面构建上使用参数化建模的方法，只需输入喉部半径、收敛段半径、上下游圆弧段半径、面积比、喷管出口角、扩张段入口角、收缩比等关键几何特征便可自动构建出喷管型线，收敛段使用双圆弧构造，扩张段为下圆弧接上拟抛物线型面，其中拟抛物线公式如下：

计算中室压PC依次取2 MPa、3 MPa、4 MPa、5 MPa、6 MPa、7 MPa、8 MPa、9 MPa、10 MPa、11 MPa、11.5 MPa、13.5 MPa、20 MPa、30 MPa；喉部半径rt取55 mm、110.1 mm、311 mm，改变喉部半径是在几何相似的情况下，相当于将喷管整体进行放大或者缩小，见图5。面积比ε取11.7、20、33，改变面积比而不改变喉部半径只是放大了喷管的扩张段，见图6。出口角度α取2°、3°、4°、6°、8°、8.436°（该值是一个喷管性能较优的值）、9°、10°、12°、14°。由于该型甲烷发动机拟采用全再生冷却设计，可认为燃气没有向壁面传热，故壁面边界条件取绝热，附面层计算使用全湍流计算，所有计算都没有进行附面层修正型面后的二次无粘计算。

图5 改变喉部半径、面积比不变的喷管型面Fig.5 Nozzle contours of different throat radius

图6 改变面积比、喉部半径不变的喷管型面Fig.6 Nozzle contours of different throat radius

3 计算结果

3.1 各类效率随室压变化的趋势

图7为不同的效率随室压的变化，其中混合比为3.5，喉部半径为110 mm，面积比为20，出口角度为8.436°。从图7 可以看出随着室压增加化学动力效率增加。这可解释为由于室压增加，密度增加，导致化学平衡向重组反应倾斜，使得燃烧室中离解反应程度降低，喷管中的化学动力损失降低，因此化学动力效率增加。但从图7中可知在其他条件不变时，改变室压对附面层效率和几何效率影响不大。

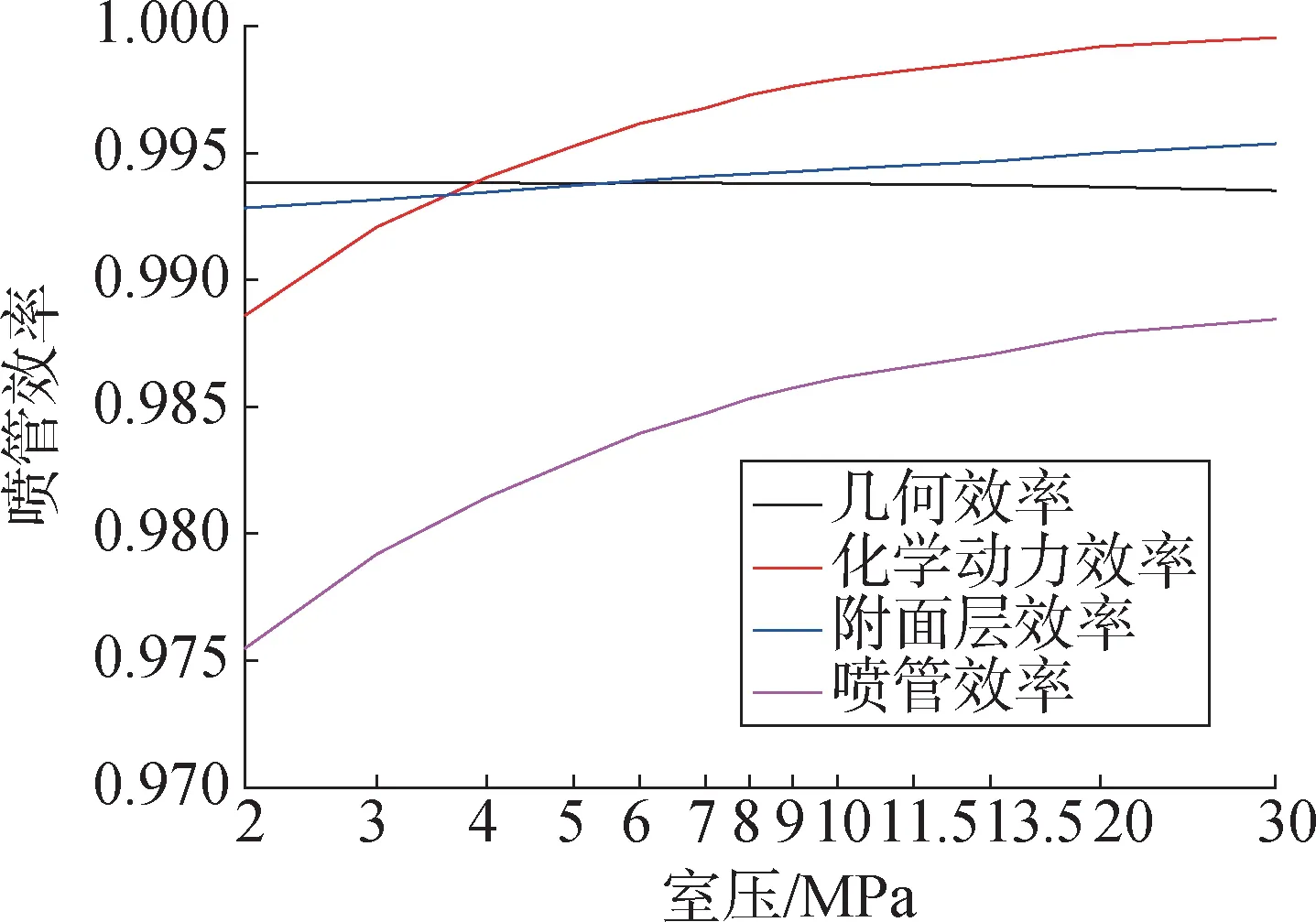
图7 不同的效率随室压的变化Fig.7 Different efficiency as function of chamber pressures

3.2 化学动力效率随室压、喉部半径和面积比的变化

图8显示了化学动力效率随室压、喉部半径、喷管面积比变化而变化的趋势，其中混合比为3.5，出口角度为8.436°。从图8 中可看出，喷管喉部半径减少，绝对长度减少，导致流体在喷管中的停留时间减少，这意味着离解产物发生重组的时间减少，使得化学动力损失增大，化学动力效率降低。而更高的面积比使得离解产物经历的冻结流动时间增加，化学能向动能的转化减少，故化学动力效率降低。但总的来说，喉部半径和面积比变化对化学动力效率的影响均不及前文讨论过的室压，而且从图8中可看出喷管尺寸越小，室压对化学动力效率的影响越大。

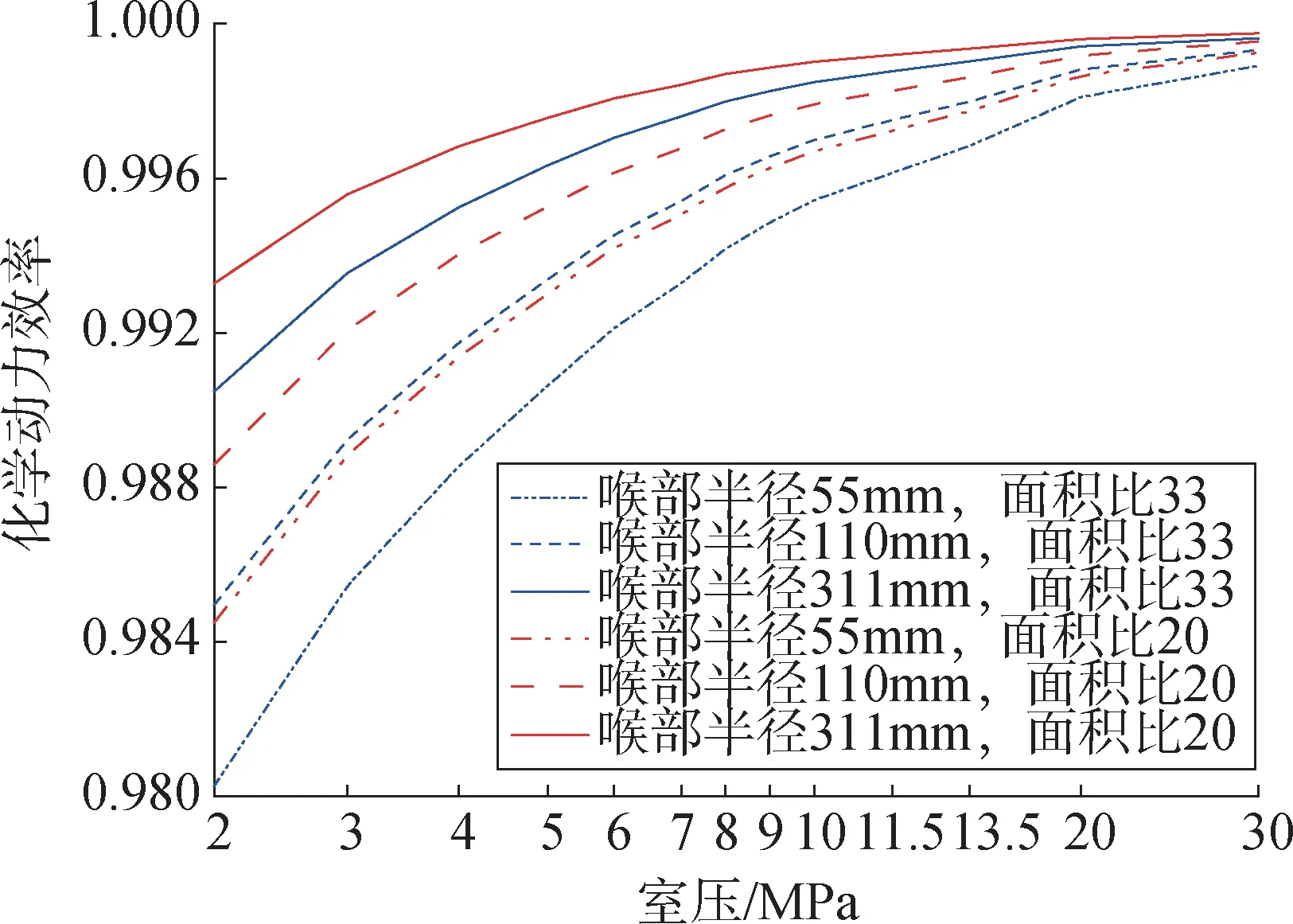
图8 化学动力效率随室压、喉部半径、喷管面积比的变化Fig.8 Kinetic efficiency as function of chamber pressure, throal radius, and exit area ratio

3.3 几何效率随室压、喉部半径和面积比的变化

图9为几何效率随室压、喉部半径、喷管面积比的变化，其中混合比为3.5，出口角度为8.436°。由图9可知几何效率随着室压增加而降低，这是因为室压越高，出口气流速度越大，出口流场愈不均匀。在室压达到14.5 MPa之前，喉部半径增加使得几何效率增加，超过14.5 MPa后，喉部半径增加使得几何效率降低。面积比增加，喷管长度增加，同样导致气流速度增大，出口流场更易不均匀，使得几何效率降低。

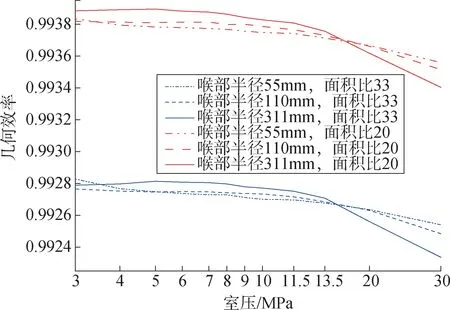
图9 几何效率随室压、喉部半径、喷管面积比的变化Fig.9 Geometric efficiency as function of chamber pressure,throal radius, and exit area ratio

3.4 附面层效率随室压、喉部半径和面积比的变化

附面层效率随喷管设计参数变化如图10 所示，其中混合比为3.5，出口角度为8.436°。更高的室压产生了更小的位移厚度（如图11 所示，其中混合比为3.5，出口角度为8.436°），因此提高了附面层效率。更大的面积比意味着更长的壁面，这会增加附面层损失，因此附面层效率随着面积比增大而减小。更大的喉部半径增加了喷管长度，位移厚度增大，但是相对位移厚度减小（如图11所示），附面层损失减少，所以最终附面层效率随着喉部半径增大而增大。

图11 出口位移厚度与喉部半径之比随室压、喉部半径、喷管面积比的变化Fig.11 Exit displacement normalized with the throat radius for different chamber pressure, throal radius, and exit area ratio

3.5 喷管效率随室压、喉部半径和面积比的变化

总的喷管效率变化规律如图12 所示，其中混合比为3.5，出口角度为8.436°，从前面的讨论可看出，对于该型甲烷发动机，随着室压增加，附面层效率和化学动力效率增加，而几何效率变化不大，故室压增加，喷管效率增加。同样的，喉部半径增加，附面层效率和化学动力效率增加，几何效率也变化不大，故喉部半径增大，喷管效率增大。而随着面积比增大，附面层效率、化学动力效率及几何效率都减小，故面积比越大，喷管效率越低。

图12 喷管效率随室压、喉部半径、喷管面积比的变化Fig.12 Nozzle efficiency as function of chamber pressure, throal radius, and exit area ratio

3.6 喷管出口角度变化对各类效率的影响

图13 展示了各类喷管效率随壁面出口角度的变化，其中混合比为3.5，室压为11.5 MPa，喉部半径为110 mm。对于该型甲烷发动机来说，标准出口角度为8.436°，不同的出口角度意味着抛物线型面的小变化（如图14 所示，其中无量纲坐标为实际单位坐标与喉部半径的比值）。化学动力效率和附面层效率随喷管出口角度变化较小，几何效率在8°左右达到最大值，之后开始减少，喷管效率在8.436°左右达到最大值。