时空分数阶扩散方程的高效数值算法研究*

向 丽,曹俊英,王自强

(贵州民族大学 数据科学与信息工程学院,贵州 贵阳 550025)

1 背景

分数阶扩散方程(FDE)是通过用分数导数代替标准导数获得的经典部分扩散方程的推广,分数阶微积分应用范围广泛,可以描述一些具有记忆性、非局部性的动态系统[1]。分数阶导数和分数阶微分方程被许多科学和工程领域的研究人员所研究[2-5]。由于分数阶算子的非局部性质,经过数值离散后,得到的线性方程组的系数矩阵往往都是稠密的,这就导致了分数阶扩散方程数值求解的时间复杂度和空间复杂度都很高,随着分数阶微分方程模型的增多和精确解的不易获得,人们对开发快速的数值方法产生了极大的兴趣。

本文研究时间上为Caputo型分数阶导数,空间上为Riemann-Liouville型的分数阶导数的时空分数阶扩散方程,对它的一个高阶数值格式进行了构造和分析。最后给出了一个数值算例证明了该格式的有效性及算法的高效性。

2 数值格式构造

考虑如下的时间-空间分数阶扩散方程的初边值问题:

(1)

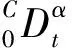
这里的Γ(·)是gamma函数。

首先分别对空间[L,R]和时间[0,T]进行等距剖分,取两个正整数N和M,定义空间网格和时间网格如下:

下面考虑时间上的离散,采用文献[7]中的离散方法:

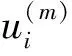
其中:

其中:

(m-1)2-α+m2-α,

Bj=2(2-α)(j-1)1-α+2(j-1)2-α-2j2-α,

IN×N为N×N阶的单位矩阵,

结合时间空间的离散格式,得如下的数值格式。

当m=1,2时有:

其中,

W=Δxβ/(ΔtαΓ(3-α)),

G(2)=ΔxβF(2)-WD0U(0),

D±=diag(d±,1,…,d±,N),

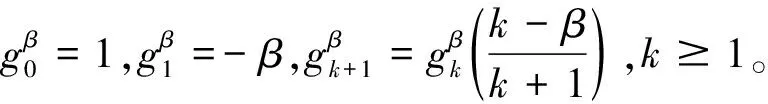
当m≥3时有:

(WC1IN×N+B)U(m)=Δxβ(F(m)-Q(m-1))(2)

其中,

简记为

AU(m)=b(m),

其中,

vM,N=WC1,b(m)=ΔxβF(m)-Q(m-1)。

系数矩阵A具有Toeplitz类结构,我们利用文献[8]中的思想方法引入两个与系数矩阵具有相同结构的预处理器,同时保持低计算成本,应考虑小带宽矩阵,第一个预处理器如下:

其中BN是一阶导数算子离散化矩阵:

第二个预处理器如下:

其中LN是拉普拉斯矩阵

预处理子P1,N适合分数阶数接近于1的情况,即β<1.5;预处理子P2,N适合于分数阶数接近2的情况,即β≥1.5。

在使用GMRES迭代方法处理线性系统AU(m)=b(m)时,利用预处理方法和快速Fourier变换方法处理离散所得的Toeplitz矩阵与向量的乘积,建立数值格式(2)的快速迭代方法。

利用文献[9]中的思想方法,我们可以证明如下定理。

定理1:数值格式(2)的收敛阶为O(Δx+Δt3-α)。

3 数值实验

本部分的数值结果均使用MATLAB R2018aIntel(R)Core(TM)i5-6200U CPU @2.30GHz 2.40GHz和12.00GB内存的电脑实现。

对方程(1),取空间区域[L,R]=[0,1],时间域[0,T]=[0,1],扩散系数为:

d+(x)=Γ(3-β)xβ,d-(x)=Γ(3-β)(1-x)β,

精确解和右端项分别为:

u(x,t)=t4x2(1-x)2,

f(x,t)=24x2(1-x)2/Γ(5-α)t4-β-

我们定义最大误差为:

当空间步长相对时间步长取到很小,时间收敛阶为:

Order1=log2(E(2Δt,Δx)/E(Δt,Δx))。

当时间步长相对空间步长取到很小,空间收敛阶为:

Order2=log2(E(Δt,2Δx)/E(Δt,Δx))。

在数值实验中α=0.5,β=1.7时,方法的数值结果如表1、表2所示。

表1 误差与时间收敛阶(Δx=1/5000)

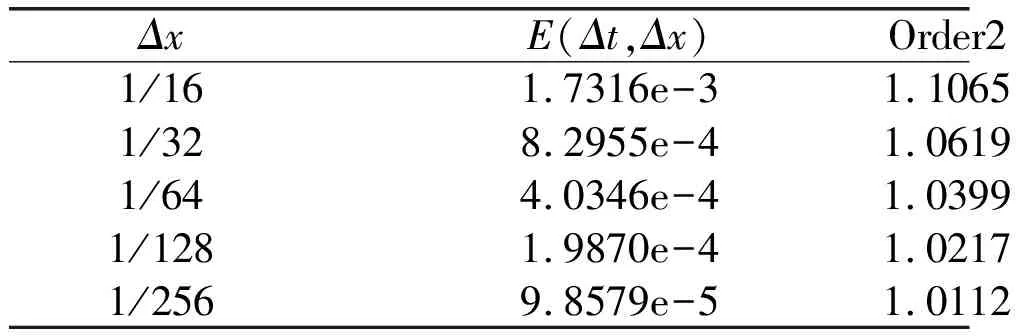
表2 误差与空间收敛阶(Δt=1/800)

从表1可以看出时间收敛阶为2.5阶,从表2可以得到空间收敛阶是1阶。这样的结论符合定理1。最后为了说明本文算法时间的有效性,我们用直接LU分解方法和本文算法进行了比较(图1)。

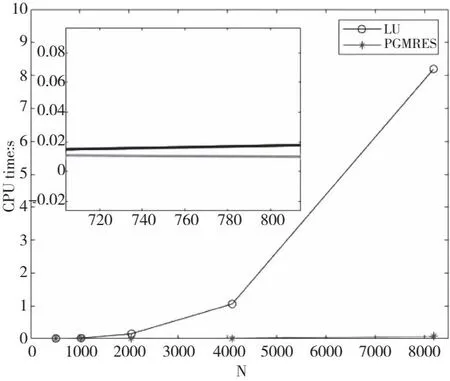
图1 比较LU与PGMRES方法所用时间(单位:s)

从图1可以看出,随着矩阵的变大,LU分解的时间增长很快,而本文算法时间变化却很平稳,所以当矩阵很大时,本文算法时间相对于直接LU分解方法所用的时间少得多。