基于最小二乘孪生支持向量机的不确定数据学习算法
2024-03-04刘锦能肖燕珊
刘锦能,肖燕珊,刘 波
(1.广东工业大学 计算机学院, 广东 广州 510006;2.广东工业大学 自动化学院, 广东 广州 510006)
支持向量机[1]是由Vapnik提出的一种用于二分类学习的监督学习模型。支持向量机可以找到最大化间隔两类的分割超平面。除了最大化间隔,支持向 量机还最小化分类误差。如今,支持向量机已广泛用于文本分类[2]、人脸识别[3]、目标检测[4]和生物医疗[5]等领域。然而,支持向量机有着O(n2)的时间复杂度,导致它不能很好地应用在大规模数据的学习问题。
为了加快训练速度,Mangasarian和Wild通过求解生成的特征值问题提出了寻求2个不平行超平面的模型[6](Generalized Eigenvalue Problem Support Vector Machine, GEPSVM) 。对于每一类数据点,GEPSVM给它们分配一个超平面,通过求解2个广义特征值问题,2个不平行的超平面就能得到,它们是2个特征向量,对应广义特征值问题的2个最小特征值。Jayadeva等[7]采用相似于GEPSVM的方法,提出了孪生支持向量机模型。类似地,它使一类的数据点靠近一个超平面,同时远离另一个超平面,从而导致求解的是2个小型的二次规划问题。与传统支持向量机需要求解单个大的二次规划问题不同,孪生支持向量机只计算2个小的二次规划问题,这使得孪生支持向量机的训练时间是传统支持向量机的四分之一[7]。孪生支持向量机已被拓展为各种变体,包括投影孪生支持向量机[8]、偏二叉树孪生支持向量机[9]和最小二乘孪生支持向量机(Least Squares Twin Support Vector Machine, LSTSVM)[10-13]。最小二乘孪生支持向量机是由孪生支持向量机衍生而来,区别在于将孪生支持向量机中的不等式约束修改为最小二乘孪生支持向量机中的等式约束。因此,用一对线性方程组代替两个凸二次规划问题可以更高效地求解该问题。
现有的有关孪生支持向量机的工作,大多假设训练数据可以准确地收集,没有任何不确定的信息。然而,由于传输干扰或测量误差,数据不可避免地包含不确定信息。为了处理数据的不确定性,Qi等[14]通过求解二阶锥规划(Second-Order Cone Programming,SOCP) 问题提出了一种鲁棒孪生支持向量机方法(Robust Twin Support Vector Machine, R-TWSVM) 用于模式识别。然而,它必须解决导致高计算成本的SOCP问题。
为此,本文提出了一种新的基于不确定数据的最小二乘孪生支持向量机方法,该方法能够高效地处理数据的不确定性。首先,考虑到数据可能包含不确定信息,引入一个噪声向量来建模每个实例的不确定信息。其次,将噪声向量融入最小二乘孪生支持向量机。最后,采用2步启发式框架求解优化问题。
1 面向不确定性数据的最小二乘孪生支持向量机
1.1 线性模型构建

所收集的实例数据x可能被噪声破坏。本文引入一个噪声向量 Δx对不确定性信息进行建模,使得真正的实例表示为x+Δx。噪声向量Δx是未知的,将在学习训练过程中得到优化。将实例表示为x+Δx,对应地,数据矩阵A和B可 以表示为A+ΔA和B+ΔB。基于上述定义,面向不确定性数据的线性最小二乘孪生支持向量机(Uncertain-data-based Least Squares Twin Support Vector Machine, ULSTSVM) 的优化公式可表示为

1.2 模型求解
由于变量ω(1),b(1), ω(2),b(2),ξ(1),ξ(2),ΔA和 ΔB是未知的,很难求解优化函数(1) 。在本文采用启发式框架来处理该优化问题,并提出了一种新的方案来评估每个训练数据点的边界参数δ1i和δ2j。
为了求解问题(1) ,本文提出了由2个步骤组成的启发式框架。第1步, ΔA和 ΔB是固定的,通过求解2个二次规划问题(3) 和(4) ,可以得到 ω(1),b(1),ω(2)和b(2)。在第2步中,ω(1),b(1),ω(2)和b(2)是固定的,更新ΔA和ΔB。2个步骤的细节如下所示。
1.2.1 固定噪声向量,求解超平面
首 先 初 始 化 ΔA和ΔB,并 确 保| |ΔAi||≤δ1i和||ΔBj||≤δ2j。然后,可以移除优化问题(1) 中的约束||ΔAi||≤δ1i和||ΔBj||≤δ2j。目标函数表示为

在问题(8) ,第1个和第2个约束式都是等式约束,将它们代入到问题(8) ,可以得到

1.2.3 启发式框架
本文采用一个启发式框架来求解目标方程(1) 。在第1步中,固定矩阵 ΔA和ΔB,然后学习分类器f1(x)和f2(x) 。在第2步中,固定学习分类器f1(x)和f2(x), 然后更新矩阵ΔA和 ΔB。在满足停止条件之前,这两个步骤将不断迭代。ULSTSVM的伪代码如算法1所示。这里使用文献[16]中的迭代停止标准来确定ULSTSVM的终止。设Fval(t)表示目标函数(1) 在第t次迭代中的值。当 |Fval(t)-Fval(t-1)|与Fmax的比值小于参数ε,算法就会终止。ε ≥0是一个非负参数。在实验中,将ε 设置为0.1。
此外,在问题(1) 中,需要给出参数 δ1i和δ2j的值。如文献[17]中所述,对于正类中的实例x1i,这里计算x1i与其k个近邻之间的距离,距离的平均值分配给δ1i。上述方法也适用于负类中的实例x2j。这样,可以得到δ1i和δ2j的值。

1.3 非线性核函数
受非线性孪生支持向量机的启发,这里将线性ULSTSVM扩展到非线性情况,旨在学习2个用核函数生成的超平面(14) 和(15) 。
2 实验与结果分析
本文将ULSTSVM与3个对比方法在不同数据集上进行比较,以验证其有效性。所有的实验都在MATLAB中运行,机器设备是一台Intel Core I5 CPU、4GB内存的笔记本电脑。在实验中,本文的目标是:(1) 在真实数据集上验证ULSTSVM的性能。(2) 当噪声数据呈百分比变化时,验证ULSTSVM的性能。(3) 验证ULSTSVM的训练时间。
2.1 对比方法与实验设置
第1个对比方法是最小二乘孪生支持向量机LSTSVM[10],它生成2个不平行超平面来分离2类数据点。然而,LSTSVM假设数据可以精确收集,并且数据中没有不确定的信息。它没有考虑数据的不确定性问题。它用于展示ULSTSVM在处理不确定数据方面的性能。
第2个对比方法是鲁棒孪生支持向量机RTWSVM[14],用于处理孪生支持向量机中的实例噪声问题。然而,它需要解决具有高时间复杂度的SOCP问题。它用于展示ULSTSVM的训练效率。
第3个对比方法是总支持向量机(Total Support Vector Classification, TSVC)[18],它是基于传统支持向量机并且考虑了数据的不确定性。
本文在UCI数据集和真实的不确定数据集上测试上述方法。本文使用准确率作为UCI数据集的评估指标,并使用F1度量作为真实不确定数据集的评估指标。在实验中,分别使用了线性核和RBF核。对于所有的方法,如果使用RBF核,核参数 σ都是从集合{10i|i=-7,···,7} 中获取。正则化参数C从集合{2i|i=-7,···,7}中获取。此外,在R-TWSVM中,参数R从集合 {0,0.01,0.02,···,0.1}中获取。在本文的方法中,计算实例的K个近邻的距离取平均值来设置实例的边界参数δ。参数K设置为0.1n,其中n是数据集中的实例数。此外,本文将阈值参数ε 设置为0.1。
2.2 UCI数据集
UCI数据集包括“Hepatitis” “WPBC”“BUPA liver”“Heart-Stalog”“Sonar”“Votes” “Australian”“German”“Breast”和 “Pima”。本文采用十折交叉验证来记录结果。对于每个数据集,将其分成相等的10个部分。在每一轮中,训练集由9个部分组成,剩下的一部分作为测试集处理,并记录准确率的平均结果。按照文献[19-21]的方法生成UCI数据集中的不确定信息。对于每一个维度,计算数据集的标准偏差σi。在[0, 2σi]范围内生成一个偏差值。然后,用生成的第i维偏差值来产生噪声数据,这使得噪声在不同维度上有所不同。将噪声随机添加到40% 的训练集实例中。训练数据加上噪声后,在UCI数据集上对ULSTSVM,LSTSVM,R-TWSVM和TSVC这4种方法进行比较。非线性核RBF下的分类准确率如表1所示。
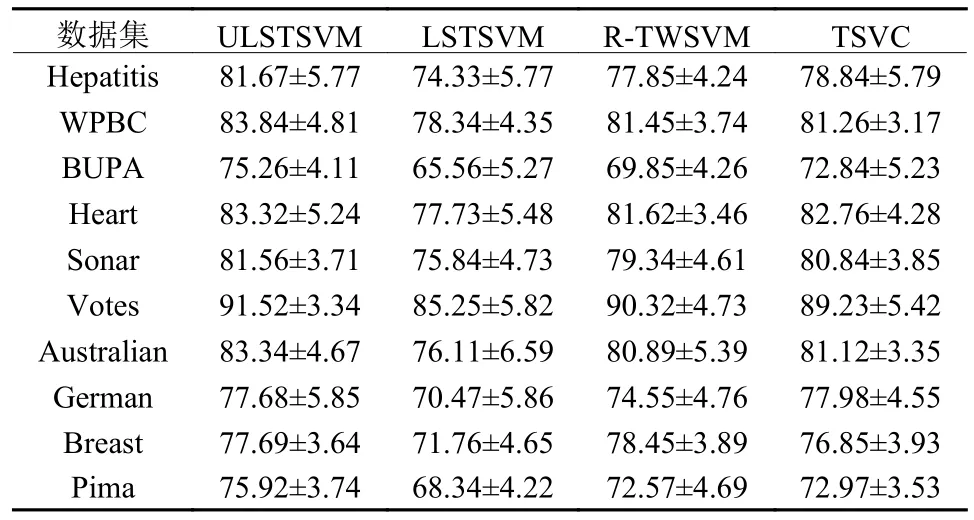
表1 RBF核在UCI数据集上的分类准确率Table 1 Classification accuracy of the RBF kernel on the UCI dataset %
从表1中可以看出,本文的方法ULSTSVM明显比LSTSVM获得更高的分类准确率,同时在大多数UCI数据集中,分类准确率与R-TWSVM和TSVC相当。本文的方法不同于LSTSVM,因为LSTSVM没有考虑到数据的不确定性。在每个实例中引入一个噪声变量来对不确定信息进行建模,并对该变量进行优化,以获得更鲁棒的分类超平面。与LSTSVM相比,ULSTSVM具有更好的性能,这表明本文的方法能够有效地处理不确定数据。
2.3 真实的不确定数据集
本文在个人活动定位数据集(Localization Data Person Activity,LDPA) 上进行了实验。LDPA是基于传感器的异常活动预测的数据集。它包含5个人的11项活动。这些活动有“摔倒”“走路”“躺下”“洗衣服”“四肢着地”等。按照文献[22]中的处理方式,将11项活动分为两类。“四肢着地”“摔倒”“坐在地上站起来”和“坐在地上”被分为正类,其余活动被视为负类。在文献[22]中,F1值用作评估指标,它是平衡精确率p和召回率r的一个指标。计算F1值的方法是F1=2pr/(p+r)。
ULSTSVM和3种对比方法在LDPA数据集上的F1值如图1所示。很明显地看到,ULSTSVM在LDPA数据集上获得了最高的F1值。具体来说,LSTSVM具有最低的F1值,因为它没有考虑数据的不确定性。此外,ULSTSVM与R-TWSVM和TSVC的分类性能相当。本文引入噪声向量Δx对不确定信息进行建模,并采用两步启发式框架求解优化问题,并且在LDPA数据集上证明了该方法的有效性。
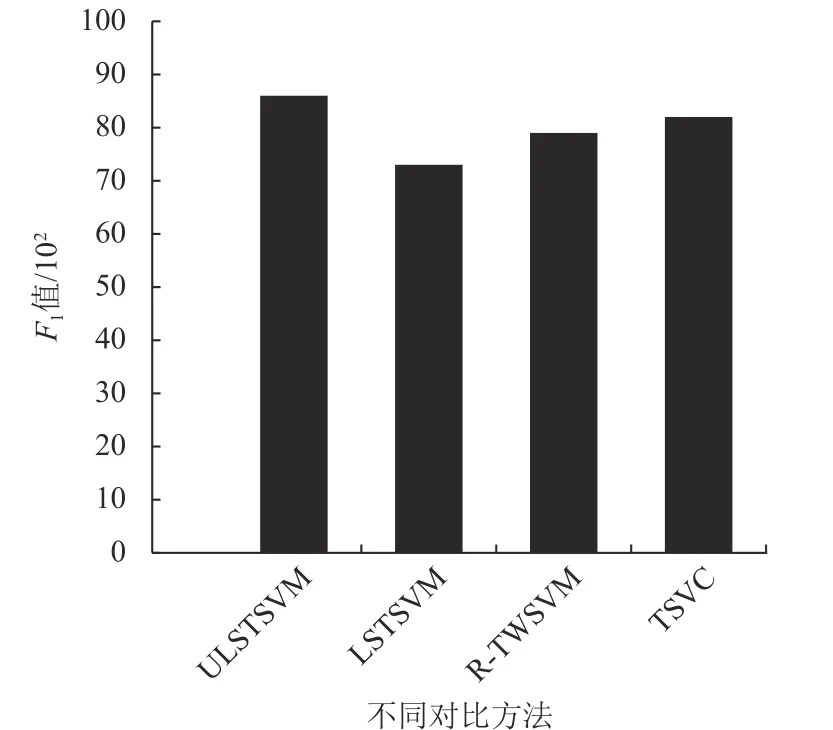
图1 不同方法在LDPA数据集上的F1值Fig.1 F1-measure values of different methods on the LDPA dataset
2.4 不同噪声水平
在本小节中,研究ULSTSVM、LSTSVM、RTWSVM和TSVC对不同数据噪声水平的敏感性。这里让噪声百分比从0%上升到100%。在图2中,x轴为噪声百分比,y轴为平均准确率。首先可以看出,当噪声百分比增加时,4种方法的分类性能同步降低。这是由于随着噪声数据点的增加,正类和负类之间的分类边界存在偏差,分类器很难对正负数据进行分类。其次,当噪声数据的比例从20%增加到100%时,ULSTSVM比LSTSVM有更高的分类准确率。因为考虑了数据不确定的影响,ULSTSVM能够获得比LSTSVM更好的分类性能。最后,ULSTSVM与RTWSVM和TSVC相比,ULSTSVM在大多数数据集上都具有更好的分类效果。

图2 不同方法在不同噪声水平数据集上的分类准确率Fig.2 Accuracy of different methods on the datasets with different levels of noise
2.5 训练时间
在上述几个小节中,研究了ULSTSVM和3种对比方法在UCI数据集和LDPA数据集上的分类性能以及对不同数据噪声水平的敏感性,本节将比较它们的训练时间。图3给出了ULSTSVM、R-TWSVM和TSVC在UCI数据集上的训练时间。首先,可以看到ULSTSVM在所有数据集上都用了最少的训练时间,是最高效的方法。其次,ULSTSVM的训练速度比RTWSVM快得多。R-TWSVM需要解决计算量较大的SOCP问题。而ULSTSVM没有像R-TWSVM那样求解SOCP问题,只是求解线性方程组,这使得本文的方法比R-TWSVM训练得更快。最后,ULSTSVM明显比TSVC快。TSVC是基于传统支持向量机的,因此它求解的是单个具有不等式约束的大规模的二次规划问题。相比之下,ULSTSVM是基于最小二乘孪生支持向量机的,因此它只需求解2个较小规模的二次规划问题,这使得ULSTSVM比TSVC更高效。
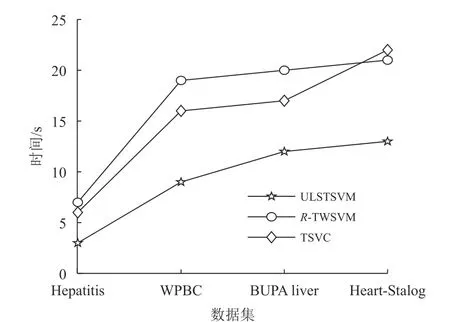
图3 不同方法在UCI数据集上的训练时间Fig.3 The training time of different methods on the UCI dataset
3 结论
本文提出了一种用于求解带有不确定数据的最小二乘孪生支持向量机模型ULSTSVM。ULSTSVM是R-TWSVM在最小二乘意义上的扩展。与需要解决SOCP问题的R-TWSVM相比,ULSTSVM更加高效,因为它只需求解线性方程组。在ULSTSVM中,首先,引入噪声向量对每个实例的不确定信息进行建模,并在训练阶段对噪声向量进行优化,使模型对噪声的影响不太敏感。其次,本文将最小二乘孪生支持向量机的思想融入到ULSTSVM中,使得这个方法比RTWSVM跑得更快。最后,采用2步启发式框架解决了ULSTSVM的学习问题。
本文的方法ULSTSVM在训练速度上超过了RTWSVM,同时也获得了相当不错的分类效果。
(责任编辑:杨耀辉 英文审核:费伦科)
