基于定子槽结构优化的交流牵引电机电磁降噪设计方法
2024-03-04张小平
傅 搏,龚 俊,张小平
(1.湖南科技大学 海洋矿产资源探采装备与安全技术国家地方联合工程实验室, 湖南 湘潭 411021; 2.湖南科技大学 信息与电气工程学院, 湖南 湘潭 411021)
0 引言
交流牵引电机因具有调速范围宽、运行可靠、维护方便等特点而广泛应用于轨道交通、电动汽车、矿用电机车等众多领域[1-3]。然而由于其运行时存在较大的噪声,对其推广应用造成了不利影响,因此对其开展降噪研究具有重要意义。
在引起交流牵引电机噪声的诸多因素中,电磁噪声是其主要因素[4],因此,如何有效抑制其电磁噪声是降低电机噪声的关键所在。目前国内外在降低交流牵引电机电磁噪声方面已开展了大量研究并提出了多种方法[4],其中尤以通过优化电机结构来降低其电磁噪声的效果较为明显,因而得到了国内外研究者的广泛重视,并取得了系列成果。其中,文献[5]对比分析了笼型感应电机转子直槽与斜槽2种结构,结果表明其斜槽结构具有更好的降噪效果;文献[6]提出了一种双斜槽的转子结构,有效降低了其电磁噪声;文献[7]则提出在转子表面开辅助槽的方法,取得了较好的降噪效果;文献[8]通过对电机定子槽宽度、定子齿开孔半径、定转子间气隙等参数进行优化,达到了降低其电磁噪声的效果;文献[9]则针对电机不同定转子槽数进行了对比分析,表明设计合理的定转子槽数能达到有效降低其电磁噪声的效果;文献[10]通过改变电机定子齿的形状,降低了其电磁噪声;此外,文献[11]还提出了一种基于定子齿肩削角的交流牵引电机降噪方法,有效降低了其电磁噪声;文献[12]则针对定子槽宽、槽高及槽底圆半径等参数进行优化,取得了明显的降噪效果;文献[13]通过对转子开辅助槽的槽型、槽宽、槽深及槽间角度等参数进行优化,取得了较好的降噪效果;文献[14]则提出在电机定子齿冠开辅助槽的方法,有效降低了其电磁噪声;文献[15]通过对比分析定转子槽宽对电磁噪声的影响,表明合理的槽宽可有效抑制其电磁噪声等。
虽然以上方法在降低交流牵引电机电磁噪声方面取得了不同程度的效果,但离实际应用要求却仍有距离,同时现有方法还存在使电机效率受到不同程度影响的问题[16]。为此,本文中提出一种基于定子槽结构优化的交流牵引电机电磁降噪设计方法。阐述了该方法的基本原理与具体设计方法,并对其进行了技术效果验证。
1 交流牵引电机降噪机理分析
如上所述,本文中针对交流牵引电机存在电磁噪声过大的问题,提出一种基于定子槽结构优化的交流牵引电机电磁降噪设计方法,该方法通过在交流牵引电机定子槽底部合适位置开出相应的矩形槽口,取得了有效抑制其电磁噪声的效果,其开槽如图1所示,具体为:首先从定子槽底部某侧边开始,在其槽宽范围内确定开槽位置,并在该位置开出相应的矩形槽口;再确定所开矩形槽口尺寸,从而达到降噪的目的。图1中,b1为定子槽的宽度,b2为定子槽某侧边至矩形槽口的距离,x、y分别为矩形槽口长、宽边的尺寸,h1为定子槽底至定子通风孔的距离,h2为定子轭部的高度。

图1 定子槽底部开槽示意图
作用于交流牵引电机定子齿表面单位面积上径向电磁力的表达式为[17]:

(1)
式(1)中:Bδ(θ,t)为气隙磁通密度;μ0为真空磁导率;μ0=4π×10-7H/m。
由式(1)可见,作用于定子齿表面单位面积上的径向电磁力取决于气隙磁通密度,而气隙磁通密度又等于气隙磁动势和气隙磁导的乘积[18],即:
Bδ(θ,t)=Fδ(θ,t)Λδ(θ,t)
(2)
式(2)中:Fδ(θ,t)为气隙磁势;Λδ(θ,t)为气隙磁导。
电机主磁通经过定子齿和定子轭、气隙、转子轭和转子齿形成闭合回路[19],其相应的磁通路径如图2所示。

图2 电机磁通路径
其中,流过定子轭部的主磁通Φ可表示为:
Φ=B2S2
(3)
式(3)中:B2为定子轭部的磁通密度;S2为定子轭部的截面积。其中磁通密度又表示为:
B2=μ2H2
(4)
式(4)中:μ2为定子轭部的磁导率;H2为定子轭部的磁场强度。
如果忽略定子槽的漏磁通,即假设其主磁通Φ全部流经其定子轭部和齿部,则针对其定子槽底部开槽处理前后的磁场分布如图3所示。

图3 定子槽底部开槽前后磁场分布图
根据安培环路定律[20],针对其定子槽底部开槽处理前,其轭部的磁压降可表示为:
U2=H2-1l2-1+H2-2l2-2+H2-3l2-3
(5)
式(5)中:H2-1、H2-2、H2-3分别表示定子轭部各段磁路的磁场强度;l2-1、l2-2、l2-3分别表示各段磁路的长度。

U′2=H2-1l2-1+H′2-2l′2-2+H2-3l2-3
(6)
式(6)中:U′2为定子槽底部开槽后定子轭部的磁压降;H′2-2为开槽处的磁场强度;l′2-2为开槽处磁路长度。
由于H′2-2>H2-2、l′2-2>l2-2,因而有U′2>U2,即定子槽底部开槽后,其轭部的总磁压降将增加,因而将导致其气隙的磁势减少,并进而导致其气隙的径向电磁力下降。
2 定子槽底部开槽处理机械强度分析
为验证在针对交流牵引电机定子槽底部开槽处理后是否会对其机械强度产生影响,对其开槽处理后的定子结构进行相应的机械强度分析,具体如下。
2.1 建立交流牵引电机有限元模型
以某交流牵引电机为例,其主要参数如表1所示,并根据表1所示参数建立其有限元模型,如图4所示。
2.2 定子槽底部开槽前后机械强度分析
首先建立交流牵引电机定子槽底部开槽处理前后的有限元模型,并任取其开槽位置h为5 mm,矩形槽口长、宽边尺寸x、y分别为3 mm、2 mm,可得其开槽前后定子槽底部有限元模型如图5所示。

表1 某交流牵引电机主要参数

图4 交流牵引电机有限元模型

图5 电机定子槽底部开槽处理前后有限元模型
然后利用Ansys软件对上述有限元模型进行应力计算,并取电机定子硅钢片材料的屈服强度为420 MPa[21],得到其定子槽底部开槽处理前后的应力分布如图6所示,其对应开槽位置处的最大应力如表2所示。由此可见,在针对定子槽底部开槽处理后,其开槽处的应力虽较开槽前有所增加,但仍远小于其材料的屈服强度,因此针对交流牵引电机定子槽底部开槽处理,不会影响其机械强度。

图6 定子槽底部开槽前后的应力分布图
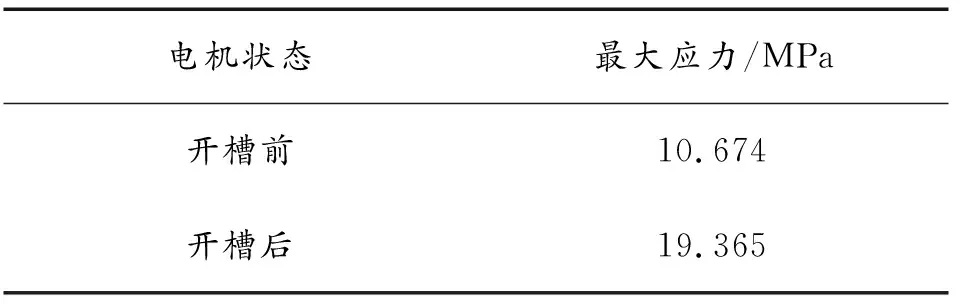
表2 定子槽底部开槽前后开槽处最大应力
3 交流牵引电机电磁噪声与模态分析
为了验证针对交流牵引电机定子槽底部开槽处理后的降噪效果,根据表1所示电机参数,首先对其进行径向电磁力阶次计算,然后利用有限元法对其进行电磁噪声与模态分析,具体如下。
3.1 交流牵引电机径向电磁力阶次计算
电机运行时,其定转子间气隙磁场会产生一系列不同阶次的径向电磁力波,而导致其电磁噪声的主要在于其低阶次的径向电磁力波[22];对于交流牵引电机来说,引起其电磁噪声的则主要为4及以下的谐波阶次。有关径向电磁力谐波阶次的计算方法为[23]:
n=μ+v
(7)
式(7)中:n为径向电磁力的谐波阶次;μ为转子绕组齿谐波极对数;v为定子绕组谐波磁场极对数。
根据式(7)及表1所示电机参数,可计算得到其径向电磁力的低阶谐波阶次,如表3所示。由表3可知,造成该电机电磁噪声的主要低阶谐波为2次和4次谐波,如能对上述低阶谐波进行有效抑制,则可达到降低其电磁噪声的目的。

表3 电机径向电磁力主要低阶谐波阶次
3.2 交流牵引电机电磁场有限元分析
根据上述所建立的交流牵引电机有限元分析模型,采用Maxwell软件进行电磁场分析,得到其定子槽底部开矩形槽口前后的磁力线分布如图7所示,其气隙磁通密度FFT分解如图8所示,其相应的谐波幅值如表4所示。由此可见,在电机定子槽底部开槽后,相应开槽位置磁力线的长度有明显的增加,而气隙磁通密度低阶谐波幅值有不同程度的减少。

图7 定子槽底部开槽前后的磁力线分布图

图8 开槽前后气隙磁通密度FFT分解图

表4 开槽前后气隙磁通密度谐波幅值
3.3 交流牵引电机径向电磁力与谐响应分析
根据上述所得,电磁场分析结果进行后处理,可得在针对电机定子槽底部开槽处理前后气隙中径向电磁力FFT分解如图9所示,其对应的低阶谐波幅值如表5所示。由此可见,在针对电机定子槽底部开矩形槽处理后,其低阶次径向电磁力2、4谐波幅值均有所下降。
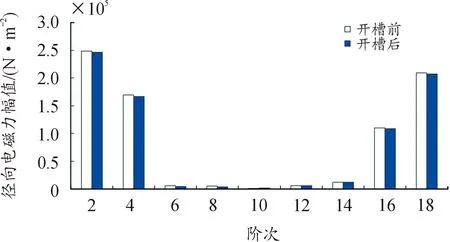
图9 开槽处理前后气隙径向电磁力FFT分解图Fig.9 FFT decomposition of air gap radial electromagnetic force before and after slotting treatment

表5 开槽处理前后气隙径向电磁力低阶谐波幅值
另外,通过谐响应分析,将径向电磁力加载至定子齿部,设置相关的约束条件和求解条件,通过后处理计算,可以得到电机定子槽底部开槽处理前后谐响应的形变如图10所示,图10中所显示的“Max”和“Min”为谐响应形变中出现的最大值与最小值,对应的幅值如表6所示。可见对定子槽底部开槽后,其形变程度与开槽前相比明显下降。
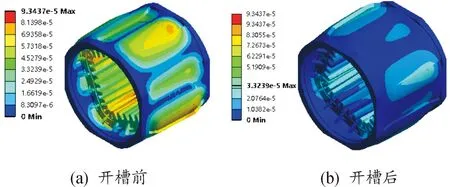
图10 开槽处理前后谐响应形变云图

表6 开槽处理前后谐响应形变最大值
3.4 交流牵引电机电磁噪声分析
根据上述所得电磁场及谐响应分析结果,利用Ansys软件对其进行声场分析,得到电机定子槽底部开槽处理前后声场强度的最大值,如表7所示,相应的最大电磁噪声及根据电磁仿真所得电机效率则如表8所示。可见,在针对交流牵引电机定子槽底部开槽处理后,其声场强度最大值下降了13.4%,电磁噪声则下降了13.3%,而电机效率基本上不受影响,可见其降噪效果十分明显。

表7 开槽处理前后声场强度最大值

表8 最大电磁噪声和效率
3.5 交流牵引电机模态分析
针对交流牵引电机定子槽底部开槽处理后,可能会对电机的固有频率造成影响。当其固有频率与径向电磁力波频率相同或接近时,将会引起共振[24],不仅会带来较大的电磁噪音,而且会对电机的正常运行和寿命造成不利影响,因此有必要对其进行相应的模态分析。
根据表1所示电机参数建立其有限元模型,利用Ansys软件对其进行模态分析,得到电机定子槽底部开槽后的模态振型如图11所示,相应的固有频率如表9所示;同时根据文献[25]及表1所示电机参数,可计算得到电机开槽后其径向电磁力的2阶、4阶谐波频率,分别为:f2=1 453.2 Hz,f4=2 677.8 Hz。可见,在针对电机定子槽底部开槽处理后,其2阶、4阶 模态振型的固有频率与其径向电磁力的2阶、4阶谐波频率相差甚远,因此针对电机定子槽底部开槽处理不会使其产生共振现象。

图11 交流牵引电机开槽后定子模态振型图

表9 2阶、4阶模态振型的固有频率
4 定子槽底部开槽结构参数优化
为了使本文提出的交流牵引电机定子槽底部开槽降噪方法达到最佳的降噪效果,首先确定在其定子槽底部开槽的最佳位置,再确定在定子槽底部所开矩形槽口的最佳长、宽边尺寸,具体如下。
4.1 定子槽底部最佳开槽位置确定方法
根据交流牵引电机定子槽结构参数,确定在其底部开槽的最佳位置,具体方法为:
1) 在定子槽宽范围内任取p组位置尺寸数据;
2) 针对上述每组位置尺寸处开相同尺寸的矩形槽口,并针对电机进行相应的电磁噪声分析,得到相应的电磁噪声值;
3) 根据上述所得p组电磁噪声值及其相应的位置尺寸,采用数值拟合方法得到其电磁噪声与相应位置尺寸间的函数关系式f(h)为
f(h)=a4h4+a3h3+a2h2+a1h+a0
(8)
式(8)中:f(h)为电磁噪声函数;a4、a3、a2、a1、a0分别为电磁噪声函数的系数;h为定子槽底部开槽位置尺寸。
4)针对式(8)求极值,得到电磁噪声取极小值时对应的开槽位置尺寸,即为最佳的开槽位置尺寸。
4.2 定子槽底部开槽最佳槽口尺寸确定方法
鉴于在交流牵引电机定子槽底部所开矩形槽口的长、宽边尺寸对其降噪效果影响较大,提出采用NSGA-Ⅱ遗传算法对其进行优化,以获得相应的最佳降噪效果,具体方法如下。
4.2.1构建优化目标函数
以交流牵引电机定子槽底部所开矩形槽口的长、宽边尺寸为优化对象,以电机电磁噪声和效率为优化目标,构建相应的优化目标函数,具体为:
1) 根据交流牵引电机定子槽结构参数,确定在其槽底开矩形槽口的长、宽边尺寸取值范围,并在该范围内任取n组数据;
2) 根据上述所确定的每组矩形槽口长、宽边数据,针对电机进行有限元分析,得到其相应的电磁噪声与效率数据;
3) 根据上述所得n组电磁噪声、效率值及其相应的矩形槽口长、宽边尺寸数据,采用数值拟合方法,分别得到其电磁噪声和效率与其槽口长、宽边尺寸间的函数关系式为

(9)
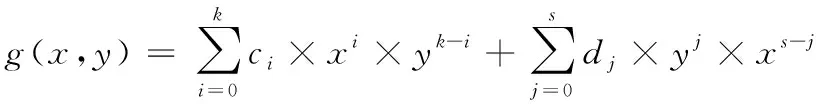
(10)
式(9)、式(10)中:f(x,y)和g(x,y)分别为电磁噪声和效率函数;x为矩形槽口长度,y为矩形槽口宽度;ai、bj分别为函数f(x,y)中的系数;ci、dj分别为函数g(x,y)中的系数;n、m分别为函数f(x,y)中的项数;k、s分别为函数g(x,y)中的项数。
4) 针对上述所得函数关系式,分别以最小化电磁噪声和最大化效率作为其优化目标,并分别以f1(z)和g1(z)表示其目标函数,即
f1(z)=f(x,y)
(11)
g1(z)=1/g(x,y)
(12)
式(11)、式(12)中:f1(z)和g1(z)分别为电磁噪声和效率对应的目标函数。
4.2.2槽口尺寸优化方法
根据上述所得优化目标函数,采用NSGA-Ⅱ遗传算法对其进行寻优[26],以获得相应的最佳矩形槽口长、宽边尺寸,具体步骤为:
步骤1确定初始化种群个体数量N,设置最大迭代次数Dmax,取迭代次数v的初始值为1;
步骤2随机生成第v代父代种群Rv;
步骤3将第v代父代种群Rv通过选择、交叉、变异生成该代子代种群Pv,并将Rv与Pv合并得到第v代种群Hv;
步骤4将种群Hv中每个个体zvi(i=1,…,2N)代入目标函数f1(z)和g1(z)中,得到相应的目标函数值f1(zvi)和g1(zvi);
步骤5根据步骤4所得各个个体的目标函数值,采用NSGA-Ⅱ遗传算法进行优化,得到下一代父代种群Rv+1;
步骤6判断迭代次数是否达到最大迭代次数Dmax,若达到,则进入步骤7;否则,将迭代次数v加1后,返回步骤3;
步骤7输出父代种群Rv+1,构建决策权重函数u(z(v+1)i),具体为
u(z(v+1)i)=m1f1(z(v+1)i)+m2g1(z(v+1)i)
(13)
式(13)中:m1为电机电磁噪声的权重系数;m2为电机效率的权重系数,且m1+m2=1。
步骤8根据式(13)计算每个个体对应的决策权重函数值,取其中最小值对应的个体作为最优解,即可得到相应矩形槽口的最优长、宽边尺寸。
5 仿真分析
为了验证本文中提出的基于定子槽结构优化的交流牵引电机电磁降噪设计方法的效果,以表1所示电机参数为例进行验证分析。首先根据表1所示电机参数,在其定子槽宽范围内任取11组开槽位置尺寸数据,如表10所示;再针对每组位置尺寸处,开出相同尺寸的矩形槽口,如任取矩形槽口长、宽边尺寸分别为x=1 mm、y=1.2 mm;之后针对开槽后的电机进行有限元分析,得到相应的电磁噪声值,如表10所示。
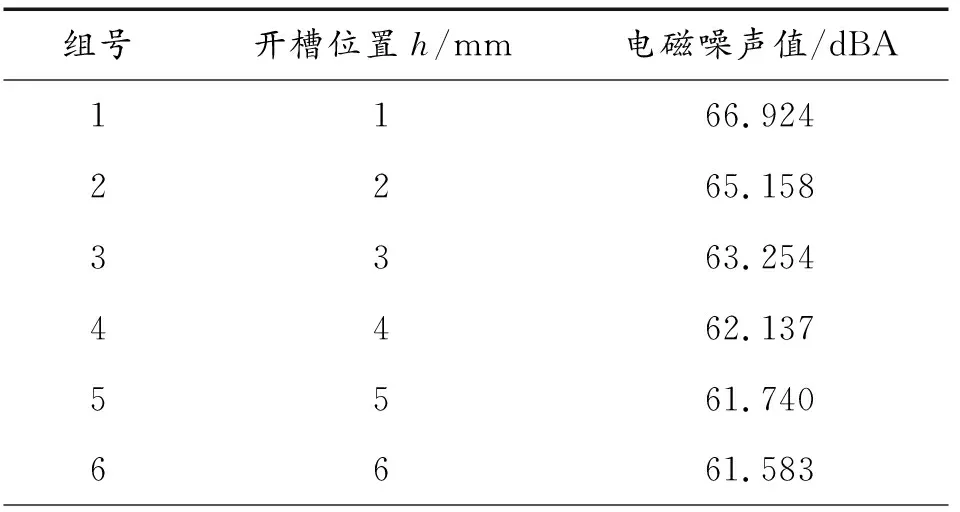
表10 开槽位置及相应的电磁噪声值

续表(表10)
根据表10所得开槽位置尺寸及其对应的电磁噪声值,采用最小二乘法得到其电磁噪声与相应位置尺寸间的函数关系为:
f(h)=-0.003 012h4+0.061 1h3-0.144 1h2-
1.902h+68.96
(14)
对式(14)求极值,得到其电磁噪声取极小值时对应的开槽位置尺寸,即为最佳开槽位置尺寸,具体为h=5.42 mm。
再根据电机结构参数,可得在其定子槽底开矩形槽口的长、宽边尺寸取值范围,分别为0~8 mm、0~10 mm,并在该范围内任取25组长、宽边尺寸数据;针对每组长、宽边尺寸数据,在上述所得最佳开槽位置尺寸处开相应的矩形槽口,并进行有限元分析,得到相应的电磁噪声和效率值,如表11所示。
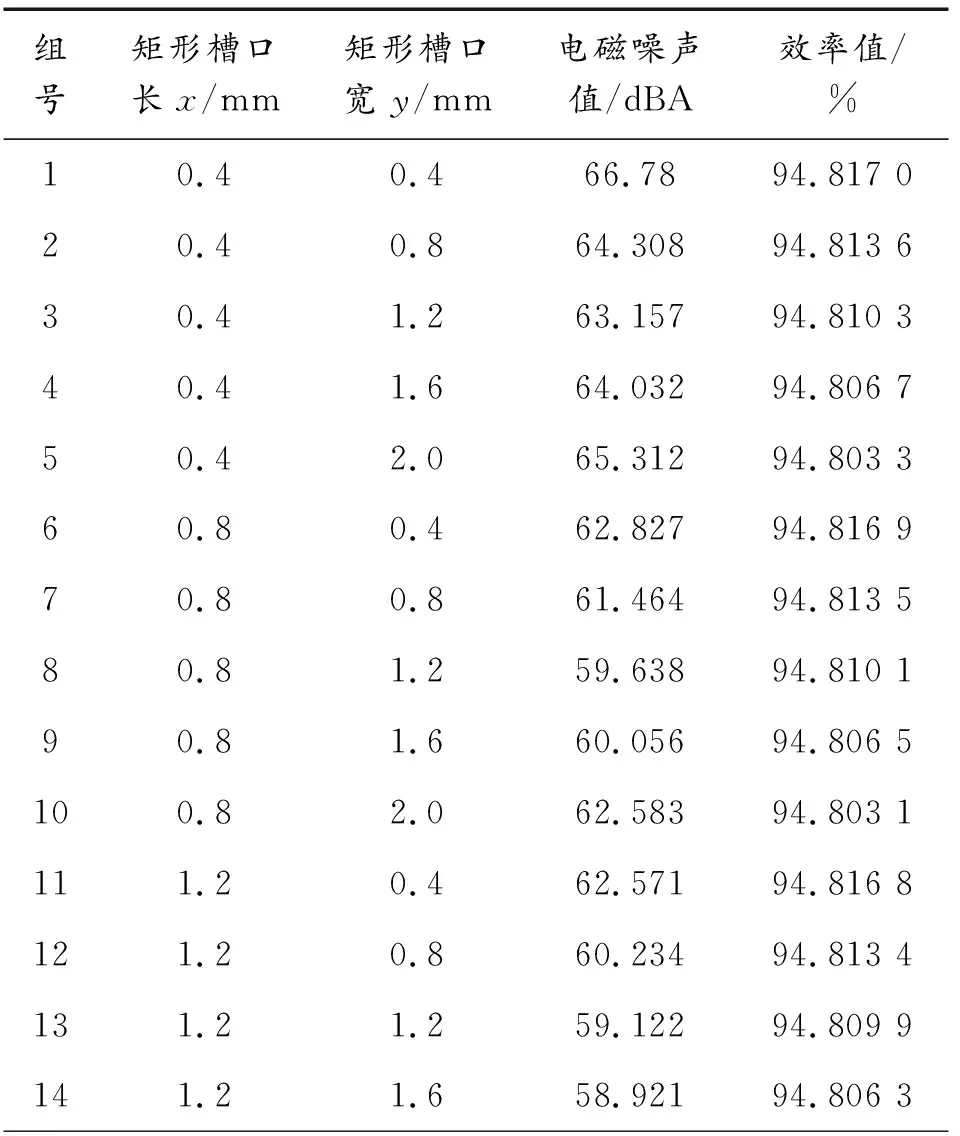
表11 电机电磁噪声和效率值及其对应的 矩形槽口长、宽边尺寸数据
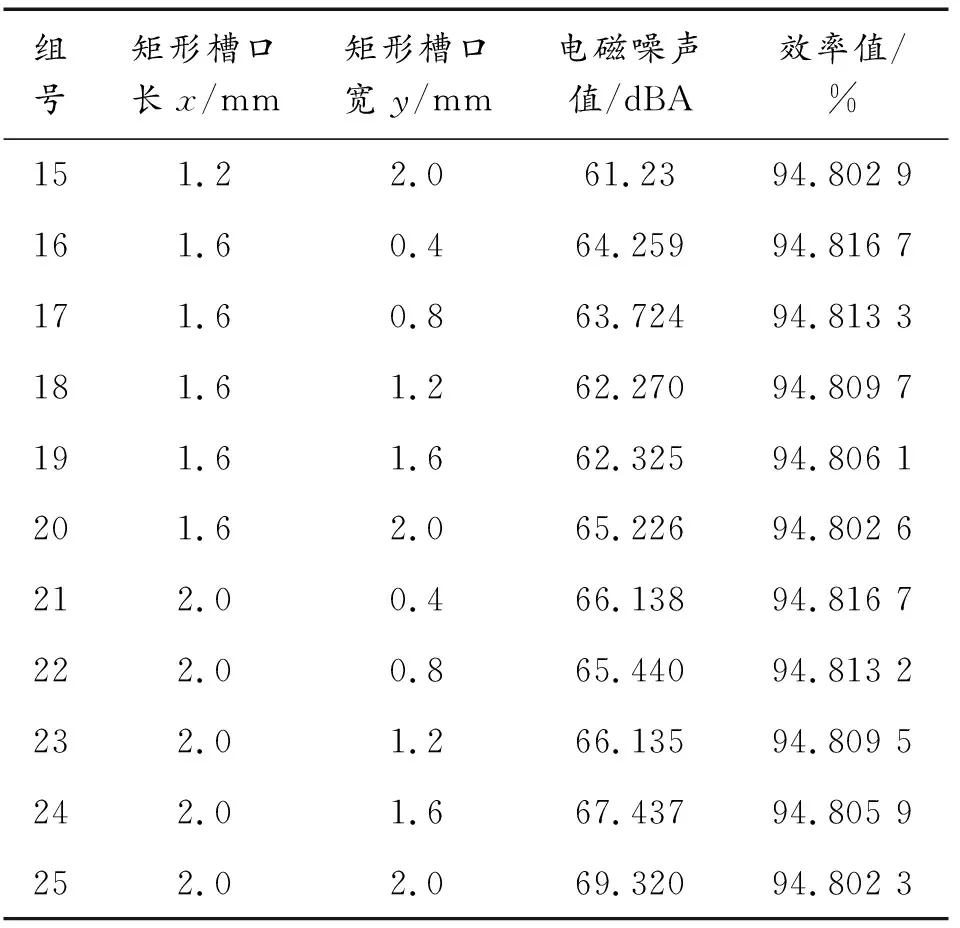
续表(表11)
根据表11电磁噪声和效率及其相应的矩形槽口长、宽边尺寸数据,采用最小二乘法进行数值拟合,分别得到电磁噪声和效率与其矩形槽口长、宽边尺寸间的函数关系为:
f(x,y)=68.53+14.48x-6.047y-45.95x2- 0.666 8xy-0.241y2+36.49x3-1.743x2y+ 1.264xy2+0.987 6y3-8.776x4+2.185x3y- 1.637x2y2+0.456 1xy3
(15)
g(x,y)=94.82-2.367×10-4x+7.157×10-3y+ 3.125×10-5x2-1.143×10-4xy- 1.165×10-3y2+2.604×10-5x3- 1.116×10-4x2y+4.464×10-5xy2+ 2.865×10-4y3
(16)
f1(z)=f(x,y)
(17)
g1(z)=1/g(x,y)
(18)
以式(17)和式(18)所示函数关系式作为优化目标函数,并采用遗传算法对其进行优化,同时任取权重系数m1、m2分别0.6和0.4,得到其最优解,即其矩形槽口的最佳长、宽边尺寸,分别为:x=1.08 mm,y=1.355 mm。
根据上述所得最佳开槽位置尺寸及最佳矩形槽口长、宽边尺寸,对电机定子槽底部进行开槽处理,并进行相应的有限元分析,得到相应的电磁噪声和效率值;同时为便于对比分析,根据表1所示参数对电机开槽处理前进行相同的有限元分析,得到其电磁噪声和效率值,如表12所示。

表12 开槽处理前后电机电磁噪声与效率值
可见,采用上述最佳开槽位置尺寸及最佳矩形槽口尺寸对交流牵引电机定子槽底部进行开槽处理后,其电磁噪声相对于未开槽前下降了17.808 dBA,即下降了23.3%,而电机效率则基本上不受影响。
6 结论
针对交流牵引电机存在电磁噪声过大的问题,本文中提出一种基于定子槽结构优化的交流牵引电机电磁降噪设计方法。分析了交流牵引电机产生电磁噪声的根本原因,研究了在其定子槽底部开槽降噪的具体设计方法,并对其结构参数进行了优化研究,最后对其降噪效果进行了仿真验证,得到如下结论:
1) 通过采用本文中提出的交流牵引电机定子槽结构优化设计方法,使电机电磁噪声由优化前的76.454 dBA下降至优化后的58.646 dBA,即下降了23.3%,可见其降噪效果明显;
2) 在针对电机定子槽结构进行优化设计后,电机效率没有出现下降现象,而略有提升,因此,上述技术方法能够有效克服传统方法在电磁降噪优化设计中所存在的使电机效率受到不同程度影响的问题。
