矿山“生产冒进行为”的演化博弈分析

王 震 路增祥

(辽宁科技大学矿业工程学院,辽宁 鞍山 114051)

“生产冒进行为”是指矿山不具备安全生产条件时,生产提前、超能力生产或未按正常流程生产的不安全行为。 这种不安全行为主要产生于矿山企业管理者和生产工人两大群体中,是在逐利思想驱动下发生的违背矿山正常生产规律与程序的行为。 经营管理层为使企业获得更大的效益,工人为获取更多的超产奖励,难以避免地会产生各种“生产冒进行为”,形成矿山生产过程中的重大潜在风险,进而对矿山生产安全带来较大威胁。 矿山安全管理者和作业工人心理素质[1]、安全认知水平和自我效能感[2]较低,是导致矿山企业因“生产冒进行为”发生安全事故的重要原因。 因此,分析矿山企业“生产冒进行为”的发生及其演化,研究预防“生产冒进行为”发生的对策,是提升矿山安全生产管理质量的一项重要内容。

不少学者[3-4]从不同角度、采用不同方法,对工人不安全行为产生机理和预防措施等进行了大量研究,并取得了丰硕成果。 如张江石等[5]采用动态演化博弈分析方法构建成本收益矩阵,针对工人脱岗行为和企业监管行为进行了研究,得出了工人脱岗行为产生的原因。 韩帅等[6]采用心理学方法,将前景理论和心理账户理论引入到安全行为和监管行为的演化博弈决策中,通过构建前景收益感知矩阵并分析其收敛性,来判断两种行为是否处于理想状态,为工人不安全行为的监管提出了相应策略。 李停军[7]构建了工人和工人、工人和监管者的博弈模型,在对模型定性、定量分析和求解的基础上,研究了工人不安全行为的演化规律,为不安全行为防控提供了组合干预原则与方法。 盖丽丽[8]在建立和分析安全监管人员与工人间动态博弈模型的基础上,提出了具有累积特征的、以阶段性奖惩和安全积分管理为目标的激励约束机制,以有效控制工人不安全行为发生。 杨雪等[9]通过构建“矿工情绪监管—矿工不安全行为”的动态博弈模型,研究了工人情绪引发的不安全行为所产生的潜在风险与成本,提出了通过人为干预提高工人情绪的监管效率和减少不安全行为的措施。 生产班组是矿山企业生产实施的最小组织单元,班组长同时具有本班组兼职安全员的职责,对本班组的生产组织、实施与安全监管起着重要作用。 班组长的违章指挥是导致班组成员违章作业不可忽视的原因。 为实现对违章行为的有效约束[10],李琰等[11]基于价值感知理论,构建了作业班组工人不安全行为与违章指挥、违章作业的博弈模型,得出了违章指挥和违章作业产生的主要原因。 上述基于博弈理论的不安全行为研究,为分析工人不安全行为产生原因,建立有效的约束机制与激励措施[12-13]提供了有效方法。

矿山企业生产过程中,在矿产品市场价格波动和企业全员逐利思想的双重影响下,“生产冒进行为”能够对企业的安全生产状态带来重大影响。 分析与研究矿山“生产冒进行为”产生的原因,对由此引发的矿山安全事故进行有效防控是十分必要的。 因此,本研究基于演化博弈理论,分析矿山“生产冒进行为”在工人群体产生的机理,为进一步研究矿山安全生产风险防控策略提供参考。

1 “生产冒进行为”状态函数构建

“生产冒进行为”产生于矿山经营管理层与生产工人两大群体。 对于工人而言,主要与工人的心理因素、认知水平和自我效能有关。 当这3 个因素处于较低水平时,可认为工人处于不稳定状态,也即存在不安全行为产生的风险。 以T(X)表示工人的不稳定状态函数,则有:

式中,O为工人心理因素水平;S为工人认知水平;Z为自我效能水平。

当工人长期处于不稳定状态或处于不稳定状态的工人占工人群体比例较大时,很大程度上会导致不安全行为发生[14]。 因此,若工人处于不稳定状态时,记T(X)= 0,表示工人的“生产冒进行为”一定会发生;若工人状态稳定时,记T(X)= 1,表示工人行为安全。 此时,工人的“生产冒进行为”状态函数γ(x) 可表示为

2 “生产冒进行为”演化博弈模型

2.1 演化博弈模型构建

2.1.1 “博弈”对象主体与假设条件

研究生产工人群体的“生产冒进行为”,涉及到工人“生产冒进行为”的发生与安全监管者对冒进行为的遏制两个“博弈”对立面。 因此,构建“生产冒进行为”演化博弈模型时,研究对象为工人和安全监管者。 模型建立时,假设服从以下条件:

(1)当工人处于不稳定状态时,即发生不安全行为。

(2)工人处于不稳定状态时,安全监管者的管控起到了作用,无需采取其他风险控制措施。

(3)工人和安全监管者均属于有限理性个人[15],都是为实现自我利益最大化去寻求策略,双方博弈策略有且仅有[安全行为,“生产冒进行为”]和[不监管,监管]两种状态。

2.1.2 博弈双方策略

根据双方博弈策略,本研究构建的“工人—安全监管者”博弈树模型如图1 所示。

由图1 可知:安全监管者存在监管和不监管两种情形,而工人为实现自身利益最大化,可能选择安全行为或“生产冒进行为”。 因此双方博弈存在4 种情况,即情况1:[监管,行为安全],对应收益为[W1,V1];情况2:[监管,“生产冒进行为”],对应收益为[W2,V2];情况3:[不监管,行为安全],对应收益为[W3,V3];情况4:[不监管,“生产冒进行为”],其对应收益为[W4,V4]。

2.1.3 模型参数确定

依据矿山企业安全行为监管情况[16],共设定9个主要模型参数,具体含义见表1。

表1 模型参数及其含义Table 1 Model parameters and their meanings

根据表1 给出的9 个模型参数与工人和安全监管者收益情况的关系[17],构建的工人和安全监管者收益矩阵,如表2 所示。

表2 工人和安全监管者收益矩阵Table 2 Matrix for benefits for workers and safety regulators

2.2 模型分析

以Un表示工人的期望收益,其中U1表示工人行为安全的期望收益,U2表示工人“生产冒进行为”的期望收益。 根据表2 中工人行为收益与安全监管者监管策略的关系可知:当工人行为安全时,安全管理人员的监管概率为y,不监管概率为1-y,因此,可得出工人行为安全时的期望收益U1为

当工人进行“生产冒进行为”时,对应于安全监管者的两种监管策略,可得出工人进行“生产冒进行为”时的期望收益U2为

记工人行为安全的概率为x,“生产冒进行为”概率则为1-x,结合不同状态下的工人收益U1和U2,可得出工人的平均期望收益A为

由于工人群体是理性的,因此在博弈中,工人会选择有利于自身的博弈策略。 令工人行为安全的概率变化率为dx/dt,则工人群体收益复制动态方程Ut可表为

记Kn表示安全监管者的期望收益,则安全监管者在监管时的期望收益K1进行如下计算:

不监管时的期望收益K2可通过下式得出:

此时,根据式(7)和式(8)可求得平均期望收益B(式9)和安全监管者的期望收益复制动态方程Kt(式10)。

通过对工人行为和安全监管者监管行为的效益动态分析,可得到工人和安全监管者的总体博弈复制动态方程为

3 工人不安全行为SD 博弈过程

3.1 SD 模型建立

为系统分析工人与安全监管者的博弈演化机理,根据工人期望收益U1和U2以及安全监管者期望收益K1和K2,并结合二者总体博弈复制动态方程,采用系统动力学(SD)软件,建立了含有2 个水平变量、2 个速度变量和13 个辅助变量的SD 模型,如图2所示。

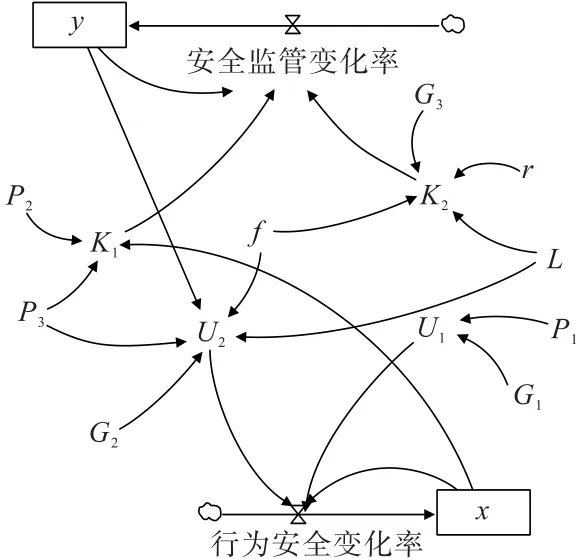
图2 工人不安全行为演化博弈系统动力学模型Fig.2 Dynamic model of evolutionary game system of workers′ unsafe behavior

3.2 参数选取

(1)在满足博弈过程限制条件的基础上,选取进行博弈的基础参数见表3[18]

表3 参数赋值情况Table 3 Parameter assignments

。

(2)假设博弈过程持续100 周,则博弈初始时间为0,终止时间为100。 其中,安全监管者以固定监管频率4 次/d 对工人进行定期检查,时间步长为0.031 25。

(3)由于工人和安全监管者均属于理性个人,故在本研究中,工人行为安全概率和安全监管者监管概率均为0.5。

3.3 SD 模型仿真模拟

根据表3 给出的参数赋值,采用系统动力学软件对8 种博弈状况进行模拟,分析参数变化对博弈双方行为选择的影响。 博弈模型随P1、P2、P33 个成本参数的变化特征如图3 所示。

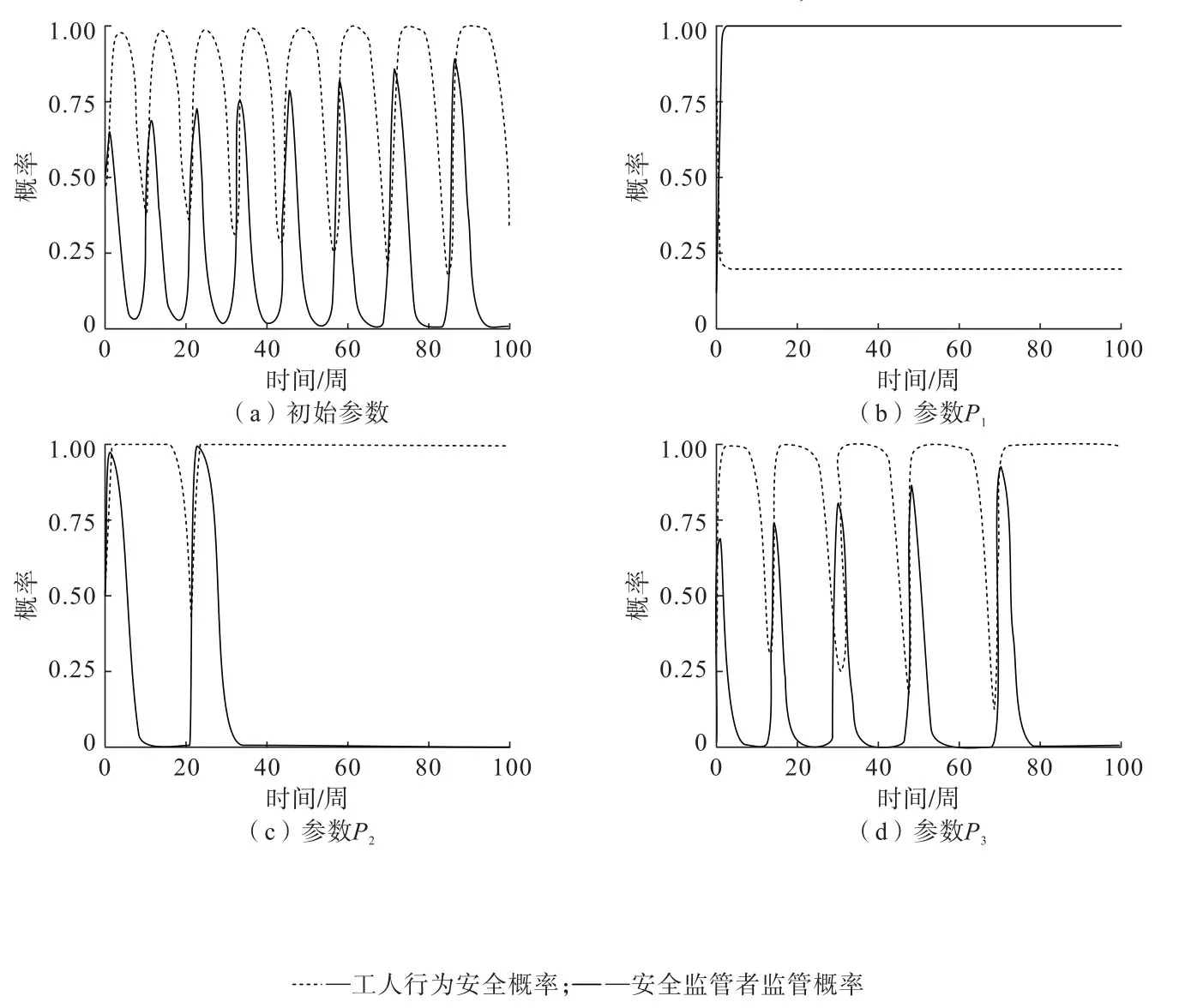
图3 初始参数和成本参数变化时的演化博弈过程Fig.3 Evolutionary game process during the variation of initial parameters and cost parameters

分析图3 可知:

(1)当工人为达到稳定状态所需付出的成本(P1)增加后,工人行为安全概率快速下降,使得“生产冒进行为”增多,安全监管者为遏制生产事故发生,倾向于实施监管行为。

(2)当工人不稳定状态提高时,安全监管者付出的成本(P2)增加,安全监管者和工人会根据各自收益变化情况进行短暂的动态博弈;当工人行为安全的概率为1 时,安全监管者不进行监管。

(3)当安全监管者加大对不稳定状态工人的经济惩罚(P3)时,工人在短期内会减少“生产冒进行为”的发生,随后由于安全监管者的监管概率下降,工人行为安全的概率也降低。 5 周后,根据收益情况,博弈双方开始新的博弈。

博弈模型随G1、G2、G33 个收益参数与风险成本参数L的变化特征如图4 所示。

图4 风险成本和收益参数变化的演化博弈过程Fig.4 Evolutionary game process during the variation of risk cost and return parameters

分析图4 可知:

(1)当工人的不稳定状态提高,导致事故发生时工人承担的风险成本(L)增加,使得动态博弈过程变缓,工人的行为选择和安全管监管者的监管选择变化周期更长,安全生产状况更稳定。

(2)当工人处于稳定状态的收益(G1)提高后,工人为寻求更高的收益,会规避“生产冒进行为”的发生,安全监管者则相应减少监管行为。

(3)当工人处于不稳定状态的收益(G2)提高时,工人“生产冒进行为”增多,安全监管者倾向于实施监管行为。

(4)当安全监管者不进行监管时的收益值(G3)提高时,工人和安全监管者的行为会呈现明显的波动变化,二者为达到各自的收益最大化进行反复动态博弈,该种状态不利于矿山安全生产。

3.4 模型参数的敏感度分析

为分析生产过程中不同影响因素对工人安全行为和安全监管者监管行为的影响,本研究引入经济学中敏感度的概念分析参数的敏感度[19]。 通过改变初始模型的参数赋值,分析不同参数下的工人安全行为和安全监管者监管行为的概率变化情况,从而得出各个因素的影响程度,结果见表4。

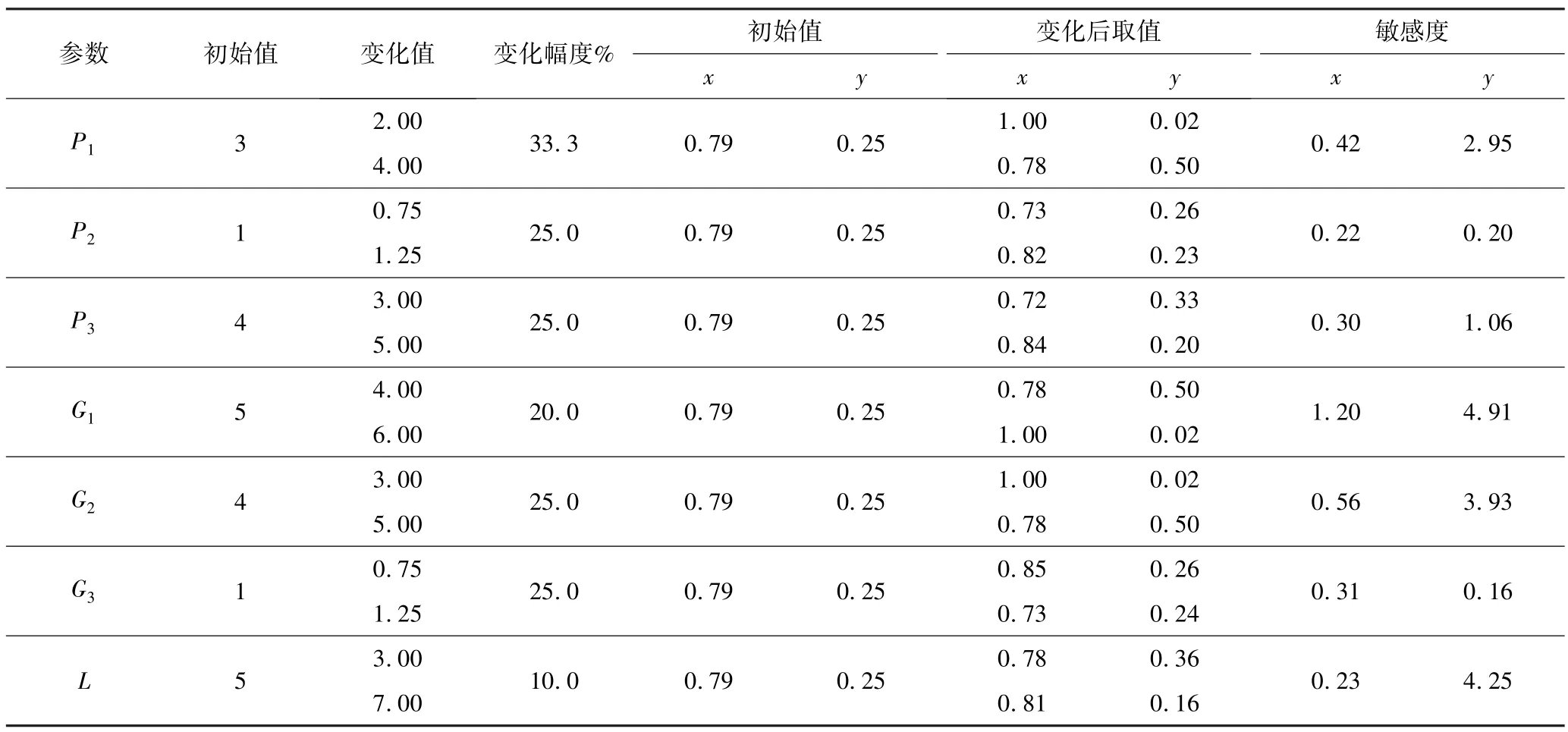
表4 各参数对工人行为安全和安全监管者监管行为的影响Table 4 Influence of each parameter on worker behavior safety and supervision behavior of safety regulators

由表4 可知:

(1)各参数对工人行为安全的影响特征表现为:① 工人处于稳定状态的收益(G1)对工人行为安全的影响最大,其敏感度为1.20,影响最小的是当工人处于不稳定状态时,安全监管者付出的成本(P2),其敏感度为0.22;② 各参数对工人行为安全的影响程度差别较小,仅当参数G1变化时,所得敏感度大于1。

(2)各参数对安全监管者监管行为的影响特征表现为:① 工人处于稳定状态的收益(G1)对安全监管者监管行为影响最大,其敏感度为4.91,影响最小的是安全监管者不进行监管时的收益值(G3),其敏感度为0.16;② 各参数对安全监管行为的影响程度差别较显著。

(3)从敏感度计算结果分析可知:对工人行为安全和安全监管行为影响程度最大的均是工人处于稳定状态的收益(G1)。 工人层面的模型参数(P1、G1、G2、L)变化对工人行为安全和安全监管者监管行为的影响程度,普遍显著于安全监管者层面的模型参数(P2、P3、G3)。 因此,为更有效地减少矿山“生产冒进行为”发生,可依据上述规律进行安全管控。

4 结 论

(1)运用演化博弈理论,依据成本效益关系构建了工人行为和安全监管者监管行为的动态博弈矩阵模型。 该模型系统考虑了影响矿山“生产冒进行为”产生的主要因素,便于有效分析其产生机理,从而为矿山生产风险管控提供参考。

(2)运用系统动力学方法,分析了工人行为和安全监管者监管行为的演化博弈过程,得出在一定范围内,工人行为安全概率和安全监管力度成正相关,但随着监管力度加大,工人会倾向于实施“生产冒进行为”。 提高安全监管者对不稳定状态工人的经济惩罚、增大不稳定状态导致事故发生时工人承担的风险成本,有助于放缓工人和安全监管者博弈过程,安全生产状况更稳定。

(3)采用敏感度理论,对影响工人行为安全和安全监管者监管行为的4 个成本因素和3 个收益因素进行了敏感度分析,得出工人处于稳定状态的收益对工人行为和安全监管行为的影响程度最大。 因此,矿山企业可根据不同因素的重要度排序,优化奖惩机制,从而降低“生产冒进行为”的发生概率。