基于人工神经网络的地震动峰值加速度预测研究

苏闻浩

（1.苏州科技大学，江苏 苏州 215009；2.江苏省结构工程重点实验室，江苏 苏州 215009）

1 引言

地震动引发的地表峰值加速度（PGA）是建筑结构抗震、结构设计环节中的重要参数。一般来说，峰值加速度的预测模型分为参数模型和非参数模型两种，参数模型一般有固定的函数表达式，其主要局限性在于需要预先定义一个表达式，并且随着研究的不断深入，表达式往往会引入更多的变量和系数，进而导致该函数表达式越发复杂。而非参数模型则是由大量数据驱动的没有固定函数表达式的模型，这种类型的模型主要缺点在于其没有固定的函数表达式形式，较难对其进行物理上的理解和分析。

现阶段，人工神经网络作为机器学习的一个重要分支，其在预测和分类问题上都取得了较大的应用进展和研究成果。在工程领域有结构位移响应、建筑模式分类等各式各样的应用场景[1]，在地震动峰值预测领域，已有不少研究人员使用人工神经网络技术创建预测模型。Kerh 等[2]使用震级、震源深度和震中距的人工神经网络来对台湾的高雄捷运系统中两个主干线上的PGA 进行估算，将预测结果与回归分析结果作比较，结果表明，神经网络的预测值更加接近实际地震记录。Thomas 等[3]提出了自适应神经网络预测系统，利用NGAwest 数据库中的2815 条数据记录对PGA 进行预测。在之后的研究中，Dhanay等[4]在之前的神经网络上又综合考虑了场地因素以及破裂机制，使用震级、震中距、破裂机制和场地Vs30预测PGA并同时验证了模型性能。

在前期的研究中，研究人员主要考虑了地震的震级、震源深度等参数，随后部分研究人员添加了场地地表下30m内的等效剪切波速（Vs30）来表征场地信息以增加模型精度。本文在这些研究的基础上，添加了发生地震时地底的峰值加速参数，对地表峰值加速度进行更加精确的预测。同时还探究了不同软硬场地情况下该模型的预测性能差异，为人工神经网络技术在抗震设计等工程应用领域提供了一些参考。

2 人工神经网络

人工神经网络是对人脑的抽象、简化和模拟，其中神经元又称感知机，是神经网络的最基本组成单位（如图1 所示），每一个神经元都由一个线性层和一个激活函数组成。神经元输出公式为：

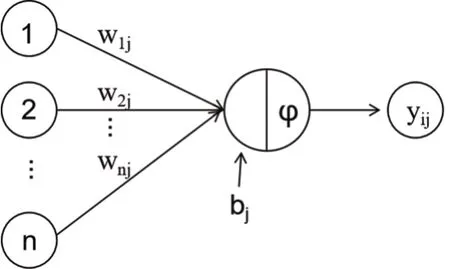
图1 单个神经元结构示意图(图片来源：作者自绘)

式中，wij指神经网络中第i 层与i-1层神经元之间的权重；bj指神经网络中第i 层第j 个神经元线性层的偏置；φ指激活函数。

神经网络内部按照不同结构位置的划分，包括输入层、隐藏层、输出层三个部分。其中，输入层每个神经元对应一个变量特征，隐藏层为使用多个神经元进行的多层组合，针对回归问题的输出层有一个神经元。每一层的神经元通过前一层的加权运算和激活运算传递数值，并通过反向传播算法实现各个权值参数的更新。若该网络的第i 层与i-1层的所有神经元全连接，则该神经网络被称为全连接人工神经网络(DNN)。

3 实验与分析

3.1 数据收集与处理

日本KiK-net（Kiban Kyoshin network）是全世界范围内应用范围最广的竖向台网，其每个台站都有地表、井下三分量高灵敏度加速度传感器，同时公开了各个台站场地的精确土层信息，是研究场地效应的优质数据来源[5]。参照董凯月[6]的数据处理与研究方法，笔者基于日本KiK-net 台网提供的共计39200条地震数据记录，通过基线校正和0.1～35Hz 滤波频段处理，对数据进行整理，最终得到了本文的数据库。数据库中PGA 分布在1～2430cm/s2之间，PGA 分布最多的区间为30～80cm/s2，占据了数据库总量的29.7%，10～30cm/s2之间的数据占据了29%，大于80cm/s2的数据占据了整体数据集的13%。

这些数据分布在497 个不同的地区，根据美国地震减灾计划中的分类标准（如表1 所示），通过Vs30进行场地类别划分。最终统计得出本数据库B 类场地共占比9%，C 类场地最多，达到了数据集的51.9%，D 类场地数据为37%，剩余数据为E 类场地数据，无A 类场地数据。

表1 地震减灾计划规范分类

3.2 人工神经网络训练

笔者选用人工神经网络作为基本框架，选用震级、震中距、震源深度、地底峰值加速度和场地Vs30作为基本输入变量，输出变量为地震动引发的PGA。最终构建了一个5输入、20个隐藏神经元、1 个输出的全连接人工神经网络，神经网络模型如图2所示。

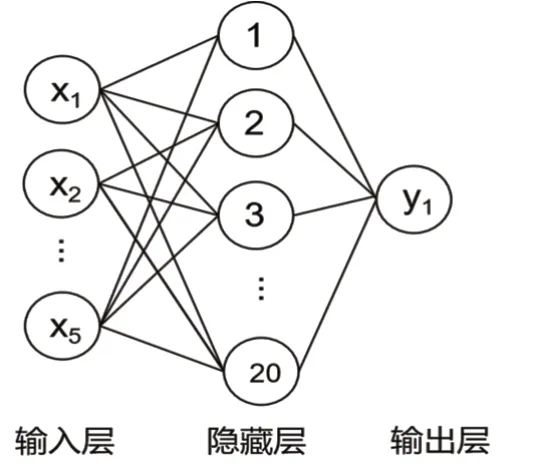
图2 神经网络模型结构(图片来源：作者自绘)

在进行神经网络训练时，将输出PGA 取自然对数处理，这样可以将目标值的分布范围减小，加速神经网络梯度的更新，有效提高神经网络的收敛速度。同时笔者采用Adam（Adaptive Moment Estimation）优化器[7]，该优化器使得超参数具有很好的解释性，仅需微调，通过其可以自动调整学习率的特性达到快速收敛的目的。

在网络优化过程中，通过分批次进行数据的输入和训练，可以有效加快学习效率。batch-size 为每个批次送入网络模型的样本量，输入过小的batchsize 会导致每次网络的训练样本数据过少，样本不具有代表性，容易出现过拟合；过大的batch-size 则会使得神经网络对样本数据的改变不敏感，很有可能陷入局部最优解，使训练效果变差。经过多次尝试，本文最终确定的batchsize 大小为256。本文同时将数据集的80%作为训练集，剩余的20%作为测试集，测试集的数据不参与训练，仅在训练完成后计算其各项评价指标以验证模型的可靠性。

本文神经网络模型代码的实现基于Python3.9 环境和Pytorch 深度学习框架。

3.3 结果验证与分析

在经历了1500 次训练迭代后，模型各方面性能趋于稳定，最终得到了训练完成后的神经网络模型。图3 为该训练完成的神经网络模型测试集上目标值与预测值散点分布图，图中横坐标表示PGA 取自然对数后的实测目标值，纵坐标表示网络模型预测值，图中实线表示预测值与实测值相等，为最佳训练效果。对测试集数据进行线性回归，回归直线图中以虚线表示。

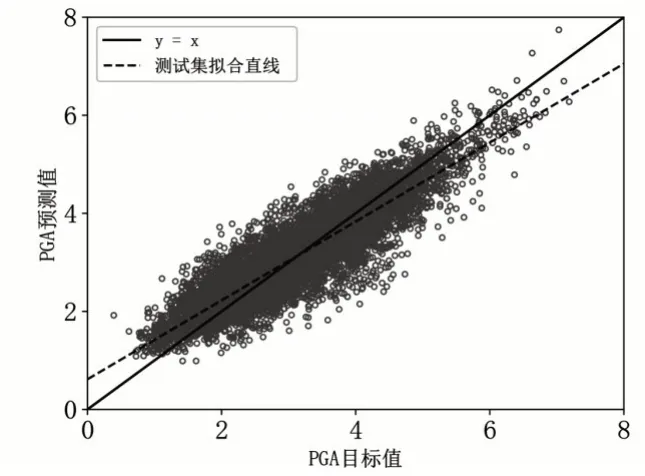
图3 神经网络目标值与预测值关系图(图片来源：作者自绘)

图3 中可见，该网络模型预测值与目标值整体分布在最佳拟合曲线周围，有较好的预测性能，在测试集上线性回归得到的斜率为0.82，相较于最佳训练效果，本模型在PGA 目标值较大时会产生相对低估的趋势。可能是由于数据库中PGA 在较高部分数据相对较少，模型的学习效果相对不充分。

为了定量地分析该模型的预测性能，将该神经网络模型的目标值与预测值之差定义为该模型的误差。在全数据集上计算其误差，得到的误差分布如图4所示。

图4 神经网络模型误差分布(图片来源：作者自绘)

通过计算得出，该模型误差的均值、方差和标准差为-0.022、0.237 和0.486。图4 中可见，该神经网络模型误差呈正态分布，均值误差接近于0，标准差较小，网络模型的误差整体呈现出无偏的特性，统计得到误差分布在-0.5～0.5之间的比例占总数目的72%，展现出了良好的预测性能。

为了分析各个场地在该网络模型中的性能表现，图5 绘制了B、C、D、E 这四类场地上各自的误差分布。由于场地类型较多，因此图中仅给出了各误差分布的包络曲线。其中B 类场地为坚硬场地，E类场地为松软场地。

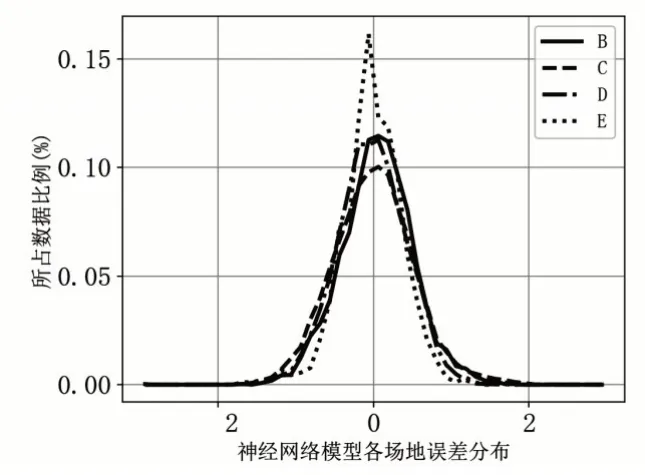
图5 神经网络模型各场地预测误差分布(图片来源：作者自绘)

如图5所示，各个场地的误差均在0附近呈现出正态分布。通过统计可得，B、C、D、E 这四类场地误差分布在-0.5～0.5 之间的比例分别为73.8%、67.7%、74.6%和83.0%。各场地的预测性能相对一致，其中E 类场地的预测性能相较于其余场地整体更好。

3.4 模型性能对比分析

本文使用机器学习任务中常用的均方误差函数（MSE）（式2）和平均绝对误差（MAE）（式3）作为损失函数及评价指标[8]，同时计算了机器学习任务中最多使用的决定系数（R2）（式4）作为评价模型整体性能好坏的指标。通常，若R2的值越接近1，则说明预测模型对实测值的拟合程度越好，当R2＞0.8 时，预估值和实测目标值之间就有很强的相关性。测试集的R2同时也可以表明模型在预测时的泛化性能是否优秀，一般认为当测试集的R2达到0.8 时，该网络模型具有比较不错的模型性能。

笔者在上述神经网络模型的基础上，将输入变量调整为以往研究人员经常使用的震级、震中距、震源深度和场地Vs30这四个输入参数，额外构建了一个用于对比网络性能的神经网络模型，将该模型作为对比模型。使用相同的数据和训练方法对该模型进行训练，并通过上文中的式（2）、式（3）和式（4）计算本文人工神经网络和该对比模型在测试集上的各项评价参数，如表2所示。

表2 网络模型各评价参数及决定系数

通过表2 可见，本文的人工神经网络模型相较于对比模型，各项评价指标均有明显提升，均方误差和平均绝对误差有一定的下降，决定系数R2由0.782提升到了0.812，提升幅度约为4%。同时，该人工神经网络模型在测试集上的决定系数高于0.8，展现出优秀的模型性能。

4 结语

当前对于地表峰值加速度的各类预测模型均有一定的缺陷，由于引起地表峰值加速度变化的原因较多，传统模型需要在考虑输入参数的前提下加上衰减、阻尼和不确定性等各种影响系数，模型较为复杂且很难较为完整地考虑各个因素对其产生的影响程度，仅能给出诸如震级等参数与PGA 的正反比关系和一个相对笼统的范围预测。

使用人工神经网络，可以在不确定具体函数式关系的情况下，直接建立一个端到端的预测模型，该模型仅需考虑影响PGA 的关键因素，如地震信息和场地信息。网络模型可以自动训练并且收敛，无需人为地去确定各项系数。本文的神经网络模型预测值与实测值整体较为接近，在神经网络模型的误差表现上，该神经网络模型的误差整体呈现出正态分布的特性，同时其均值误差接近于0，在不同软硬类场地上，该神经网络模型也展现出了大致相同的预测性能，在各类场地中均可以较好地进行PGA 的预测。同时，还与以往研究中的网络模型进行了对比，发现本文改进的模型在预测性能上具有一定程度的提升，为后续的神经网络模型研究提供一定的参考。

本文同样存在一定的不足和有待改进的地方。首先，基于数据来进行训练的神经网络模型其可靠程度主要取决于数据量的大小，本文中各类场地数据分布相对不够均匀，较为松软的E 类场地数据偏少，存在一定的训练风险。其次，对于输入参数的选取，本文借鉴了以往研究中普遍使用的参数，对于是否仍有其它重要参数会对PGA 产生明显的影响，仍然是后续研究中需要讨论的一个关键问题。