高雷诺数下交叉圆柱涡激振动的数值分析

金叶青，张俊涛，2，秦 岩，崔景芝，孙海亮

(1. 哈尔滨工程大学烟台哈尔滨工程大学研究院，烟台 265503；2. 哈尔滨工程大学船舶工程学院，哈尔滨 150001；3. 北京宇航系统工程研究所，北京 100076)

0 引言

涡激振动(Vortex Induced Vibration，VIV)是钝体在流体的作用下，钝体两侧形成交替脱落的漩涡而引起结构物振动的现象[1]。当结构物自身频率和漩涡脱落频率达到一致或者接近时，发生“锁定”(同步)现象，此时结构物的振动将大幅度增加。一方面，这种高振幅振动可能会导致结构严重疲劳甚至破坏，需要避免或减少振动的发生；另一方面，可将其用于能量收集。

目前，对涡激振动的研究大多集中在形状规则的柱体上，且多为低、中雷诺数范围内的研究，而高雷诺数涡激振动的研究相对较少，且多集中在利用涡激振动提取流动能量方面[2]。Modir等[3]研究了高雷诺数(1.5×104≤Re≤6×104)条件下，水能捕获装置弹簧刚度对涡激振动的影响。实验结果表明，系统的最大幅值和锁定频率区域与弹簧刚度密切相关，固有频率的增加会导致响应幅值的增加，系统的同步范围变宽。Chang等[4]为了提高涡激振动的同步范围和振幅，实现最大限度地将水动能转化为机械能，研究了加入被动湍流控制条件下，雷诺数最高为1.2×105的圆柱涡激振动，获得了最高达2.9的振幅比。高雷诺数下可以达到高的升力[4]，这是涡激振动能量捕获研究往往是在高雷诺数条件下进行的重要原因之一。

钝体的截面形状对涡激振动也有着很大的影响，最典型的截面形状为圆柱形，不需要考虑攻角对振动的影响。不同截面形状下的涡激振动有着不同的特性，研究表明，圆形和菱形截面柱体表现为自限制运动，而三角形和方形截面则表现为非自限运动[5]。此外，轴向变直径圆柱也是涡激振动中研究热点之一。New等[6]利用实验研究了有限长波浪圆柱脱落漩涡表现，Lin等[7]利用三维大涡模拟(LES)方法研究了大展向波长对正弦波形圆柱体的尾迹的影响。但以目前对涡激振动的研究来看，几乎没有对交叉圆柱涡激振动特性的研究。然而，从工程建筑方面来看，柱体之间常有T形、L形以及十字交叉形连接。从涡激振动能量收集方面，柱体的支撑结构或者柱体连接的发电装置，均可能会存在圆柱交叉布置的形式，因此对交叉圆柱涡激振动的研究具有重要意义。

涡激振动在能量捕获应用场景中，发电系统置于钝体内部是研究热点之一，但是柱体直径过大限制了发电系统的尺寸，减少了发电量，交叉圆柱可以很好地解决钝体内部空间受限的问题。为此，本文针对应用于能量捕获场景，利用数值仿真的方法研究了交叉圆柱的涡激振动特性，其结果在涡激振动的抑制方面也具有一定的参考意义。

1 数学模型

1.1 控制方程和湍流模型

流体控制方程为非定常不可压缩流体RANS方程

(1)

(2)

(3)

式中，ui和uj分别表示i，j方向上的瞬时速度分量；μt，kt分别为湍流和湍动能；δij为Kronecker delta符号。

雷诺应力项的引入增加了方程的未知数数量，因此本文利用湍流模型SSTk-ω两方程模型，使方程未知数个数与方程数相同，使方程组闭合。SSTk-ω两方程模型是在处理绕流问题时常用的一种模型，其考虑了湍流剪切力和压强梯度效应，在求解绕流问题的RANS方程时较其他模型更具有优势。

1.2 交叉圆柱的振动响应

交叉圆柱体以弹簧作弹性支撑，如图1所示(图中U表示水流流速)，圆柱体具有两个自由度，可在顺流向和横流向方向上做线涡激振动，每个自由度方向上的涡激振动可视为质量-弹簧-阻尼系统，则圆柱体运动的控制方程为

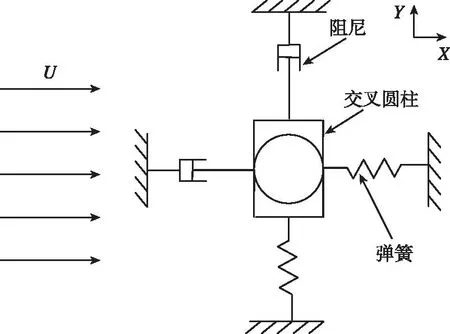
图1 二自由度弹性支承交叉圆柱VIV模型示意图Fig.1 Schematic diagram of two-degree-of-freedom elastic support crossed-cylinder VIV model

(4)

式中，x，y分别为柱体顺流向和横流向位移；m为圆柱体的质量；c为结构阻尼系数；k为结构刚度系数；FD(t)，FL(t)分别为顺流向和横流向流体力。

利用结构动力学关系，c/m=4πζfn，k/m=(2πfn)2，式(4)又可以写为

(5)

式中，D，L分别为圆柱直径和长度，fn为振动系统在空气中的固有频率，ζ为阻尼比，m*为质量比，其表达式如下

(6)

(7)

(8)

2 数值模型的建立与验证

2.1 数值模型的建立

由于交叉圆柱在轴向的不规则性，本文采用三维数值模型仿真分析。数值仿真时流体计算域的大小对计算时间和结果的准确度都有较大影响，计算域过大会造成计算资源的浪费，计算时间过长；但计算域过小会造成流体域边界对柱体模型的较大影响，无法确保计算结果的准确度。因此，本文根据已有研究文献[8-9]，在综合考虑计算机算力的情况下，设置计算域的大小如图2所示，柱体中心至流体域出口的距离取为30D，柱体至流体域入口距离取为10D，由于竖圆柱的影响，柱体与上下边界的距离取为15D，流体域的宽度为柱体长度L。

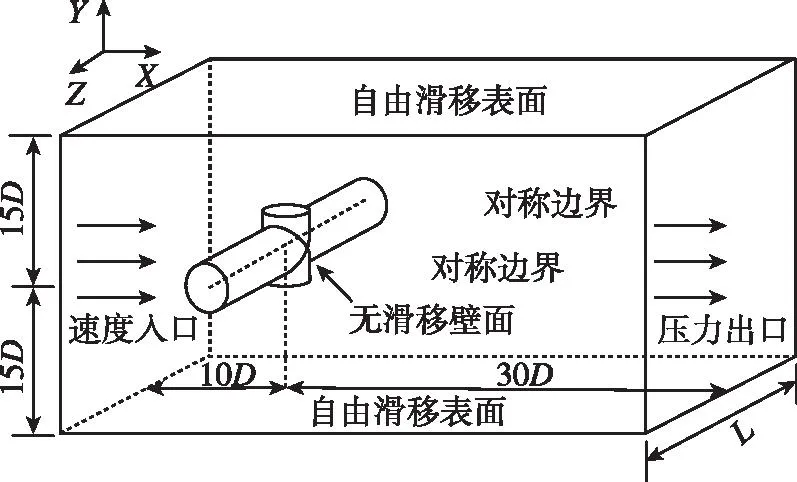
图2 交叉圆柱VIV振动模型及计算域尺寸示意图Fig.2 Schematic diagram of crossed-cylindrical VIV vibration model and calculation domain size

数值模型的X方向为水流方向，对应的计算域左右边界的边界条件分别为速度入口和压力出口，速度入口给定均匀水流的流速、湍流动能及耗散率等条件，压力出口的相对压力设置为0。计算域上下边界设置为自由滑移面，前后边界设置为对称边界，圆柱表面设置为无滑移壁面。

为避免柱体位移较大时产生网格畸变以及负网格而导致求解失败，计算网格采用重叠网格技术。重叠网格由背景网格和组分网格组成，如图3(a)所示。同时为了在较少的网格数量下保证计算精度，对柱体运动周围进行网格局部加密，如图3(b)所示。

(a)重叠网格示意图

2.2 数值模型的验证

图4 数值模型的计算结果Fig.4 The calculation results of the numerical model

3 交叉圆柱的数值仿真

3.1 模型参数

本文研究交叉圆柱的涡激振动特性时，以能量收集为应用场景，因此系统一般处于高雷诺数和高阻尼状态[11]。文献[6]研究指出，低质量比(小于1)下，振动幅值的均方根值较大，且未发现下端分支，因此，为在更宽流速范围获得较大振幅，本文交叉圆柱模型的质量比为m*=0.98。根据已有研究，高雷诺数往往会产生高振幅比[12-13]，因此本文选择了一个高雷诺数范围，为7.5×104～5×105。

交叉圆柱的直径D=0.25 m，横向长度Lh=1.5 m，竖向长度Ls=0.33 m，总质量m=77.825 kg，弹簧刚度为k=2 000 N/m。交叉圆柱的具体尺寸信息如图5(a)所示，图5(b)为交叉圆柱的VIV模型示意图，竖向圆柱的轴向也是垂直于水流流速方向。

(a)交叉圆柱尺寸

同时，为更好分析交叉圆柱的涡激振动特性，将其与普通圆柱的涡激振动做了对比分析。普通圆柱直径和质量与交叉圆柱相同，通过改变普通圆柱长度改变排水质量，可保证质量比不变。如此由式(6)可，在弹簧刚度相同的情况下，交叉圆柱VIV系统和普通圆柱VIV系统的fn相等。

3.2 仿真结果与分析

基于本文建立的数值模型，根据上述模型参数，交叉圆柱和普通圆柱在各约化速度下的振幅如图6所示，从图中可以得出下列结论。1)交叉圆柱的振幅随约化速度的变化曲线，在Ur=4.5～5之间存在明显的跳跃，即在此处由初始分支转化为上端分支，而普通圆柱振幅曲线的分支转变在Ur=3～4之间。2)在低流速区域，普通圆柱和交叉圆柱的振幅相差很大，而在Ur=11～13之间，其振幅基本相等。3)普通圆柱的启动流速要小于交叉圆柱，两种圆柱在启动流速之后经历一段较小的流速范围后，即初始分支，转变为上端分支。4)高雷诺数下的交叉圆柱和普通圆柱的振幅曲线均存在明显的初始分支和上端分支，但未发现明显的下端分支，与文献[6]研究结果相符。

图6 交叉圆柱与普通圆柱的振幅计算结果Fig.6 Amplitude calculation results of cross cylinder and ordinary cylinder

从振幅随流速的变化曲线来看，交叉圆柱与普通圆柱相比较，虽然启动流速变大，但进入频率锁定区域后，交叉圆柱的振幅更大。涡激振动应用于能量捕获时，设计工作流速一般设置在发生频率锁定时的流速范围，因此，交叉圆柱在应用于能量捕获场景时的振动表现优于普通圆柱。

涡激振动的振动是由漩涡的交替脱落引起的，其振幅大小与涡脱落方式有着很大的关系。Williamson等[14]在研究圆柱的涡激振动时，根据漩涡脱落时的旋向和一定周期内脱落数量等的不同，将尾涡脱落模式分为2T和2C模式。其中2C模式为圆柱体两侧各释放一对旋转方向相同的涡，但圆柱体两侧涡对的旋转方向相反。2T模式为半个周期内圆柱体脱落3个漩涡，且第2个涡强度要小于另外2个。

如图7、图8所示，普通圆柱在0.6 m/s(Ur=4.24)和1.0 m/s(Ur=7.07)的流速下的涡脱模式均为2C模式，但在流速为1.7 m/s(Ur=12.01)的情况下(图9)，涡脱落模式更类似于2T模式，即在半个周期内，圆柱体脱落3个涡，但不同的是，该模型的3个涡的强度相差并不明显。

图7 流速0.6 m/s时普通圆柱的涡量云图Fig.7 The vorticity cloud diagram of the ordinary cylinder at a flow rate of 0.6 m/s

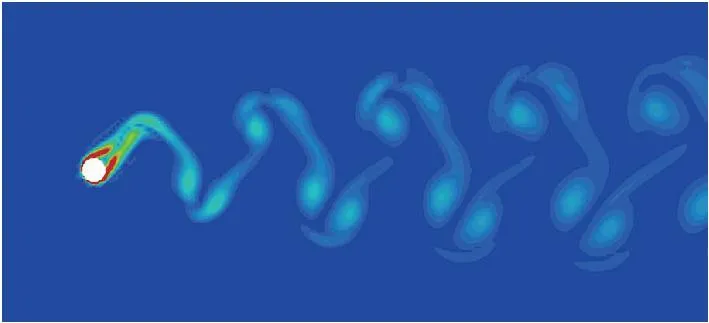
图8 流速1.0 m/s时普通圆柱的涡量云图Fig.8 The vorticity cloud diagram of the ordinary cylinder at a flow rate of 1.0 m/s

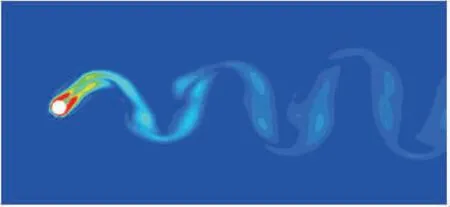
图9 流速1.7 m/s时普通圆柱的涡量云图Fig.9 The vorticity cloud diagram of the ordinary cylinder at a flow rate of 1.7 m/s

为了更清楚地了解交叉圆柱的涡脱情况，以交叉圆柱的重心为0点位置，截取了在水平圆柱轴向方向距离0点位置为0D、1D、2.5D这3个截面的涡量云图。图10呈现的是0.6 m/s流速下3种截面的涡量云图。在图10(a)中，即在交叉圆柱的交叉中心处，并没有出现完整的脱落涡，且1D的界面处受交叉圆柱的影响，也没有出现明显的脱落涡，仅在2.5D截面处可以观察到与普通圆柱相似的涡脱落模式。此外，与图7相比，相同流速下，交叉圆柱的脱落涡经过较小的距离后就会消失，因此交叉圆柱的涡强度明显低于普通圆柱，这是在0.6 m/s的流速下，交叉圆柱的振幅小于普通圆柱振幅的原因。

(a)0D

水流流速为1 m/s时，在0D截面处涡量云图如图11所示，虽然在柱体的后方尾流区域的脱落涡也不太明显，但值得注意的是，竖直柱体的上下端面处有较明显的脱落涡，即此时一部分涡并不在柱体的后方或者斜后方脱落，而是在柱体上下两个端面处脱落，而在1D和2.5D截面处，涡脱落位置与柱体的距离相比普通圆柱较小，这会使得漩涡对柱体振动的影响增加。相同流速下与普通圆柱相比(图8)，涡在脱落后的相同距离上，交叉圆柱的脱落涡有更明显的消散，这说明交叉圆柱的涡强度在该流速下依然小于普通圆柱。但是交叉圆柱的涡会在距离圆柱更近的位置脱落，这使得柱体的振动情况受涡脱落的影响更大，从而可以获得更大的振幅。

(a)0D

水流流速为1.7 m/s时，0D处截面的涡量云图如图12所示。图中可以看到脱落涡分为两部分，两侧为两个连在一起的条形涡(随水流移动两个涡合为一个)，中间有一个圆形涡，而且中间的圆形涡更像是从竖圆柱的柱面脱落下来的涡。并且在1D和2.5D截面处依旧可以观察到一个很明显的单涡，并且3处截面在半个周期内均脱落3个涡，这与普通圆柱相同。此外，与图9相比较可以看出，此时两种圆柱的涡强度以及涡脱落位置相近，所以两种圆柱的振幅也相差不多。

(a)0D

交叉圆柱的涡脱落模式与普通圆柱相比，受竖圆柱的影响很大，在0D和1D截面处都未形成与普通圆柱相似的规则涡。在低流速区域，由于竖圆柱的存在，抑制了涡的形成，涡强度减小，从而使圆柱的振幅减小。但是进入频率锁定的流速范围后，虽然竖圆柱的存在依然破坏了涡的形成，但也改变了涡脱落的位置。高流速下两种圆柱的振幅及变化均类似，这可能是交叉圆柱中的横圆柱起主要影响作用。

4 结束语

本文针对高雷诺数下交叉圆柱的涡激振动问题，建立了三维VIV数值模型，进行了仿真分析研究。为了确保模型的可靠性和准确性，利用已有文献中的试验模型参数计算出该数值模型下的仿真结果，并与文献中的试验结果进行对比，结果发现振幅比曲线具有较高的吻合度，验证了数值模型的准确性。并在此数值模型的基础上，对本文的交叉圆柱模型进行了仿真研究，并与普通圆柱进行了对比分析。

1)从振幅随流速的变化来看，交叉圆柱并没有因为竖圆柱的存在影响涡的形成，而在整个流速范围内使振幅减小，这只发生在低流速范围，并且交叉圆柱的启动流速和进入共振的流速均延后。而在进入频率锁定流速范围后，交叉圆柱的振幅反而大于普通圆柱，在Ur=11之后，两种圆柱振幅基本相等。

2)从涡脱落情况来看，在中低流速范围内，交叉圆柱的脱落涡强度比普通圆柱较弱，在低流速范围表现尤为明显，这是低流速时交叉圆柱振幅小的主要原因。但是在中流速下，交叉圆柱的竖圆柱影响了涡脱落的位置，这使得交叉圆柱的振幅不降反升。在高流速时，交叉圆柱与普通圆柱的涡脱落模式类似，且涡强度也相近，这可能是高流速下交叉圆柱的横圆柱起到了主要作用，使得振幅大小与变化与普通圆柱类似。

综上所述，交叉圆柱在解决柱体内部空间受限问题的同时，在中高流速也获得了更好的振动表现，这对应用于能量采集具有重要意义。不过，本文仅对一种交叉圆柱情况进行了研究分析，未来可对竖圆柱的直径、长度等对涡激振动的影响做进一步研究。