基于非线性有限元的网套补偿器轴向刚度特性及计算方法研究

2024-03-01王亚军陈鼎铭方红荣贺启林周浩洋

宇航总体技术 2024年1期

王亚军，陈鼎铭，方红荣，贺启林，周浩洋

(1. 中国航天电子技术研究院，北京 100094；2. 北京宇航系统工程研究所，北京 100076)

0 引言

网套补偿器是航天管路系统中广泛采用的管配件，其主要功能是减振、补偿位移。在工程实际中，钢丝网套补偿器往往承受包括温度载荷、位移载荷、内压载荷以及冲击载荷等不同形式的载荷，是管路结构中容易破坏的部位[1]。为设计高性能、高可靠性的钢丝网套补偿器，以满足日益提高的工程需求，必须对其力学性能开展深入、全面的研究。

补偿器力学分析的难点在于复杂的微结构特征：网套补偿器由波纹管与钢丝网套焊接组合而成，钢丝网套又由多锭钢丝编织而成，受载时网套和波纹管之间将发生强烈相互作用，使得网套补偿器的刚度表现出强烈的非线性[2]。

考虑到补偿器中波纹管的相关分析方法已经比较成熟，钢丝网套的分析方法是目前的研究重点。盛冬平等[3]、张程[4]、杨燕等[5]在补偿器仿真时使用基于节点耦合的梁单元建立了网套模型，评估了网套补偿器的静动力学特性。基于梁单元的网套建模方法对结构进行了较多简化，计算效率高，但难以保证准确性，且不能计算轴向变形时刚度较低的阶段。一些学者使用实体单元将网套的细观编织结构引入仿真模型，Rial等[6]、Huang等[7]建立了网套的实体模型，计算了补偿器的轴向拉伸刚度。网套实体模型比梁模型更符合实际结构，但对计算资源的要求极高，并且在轴向拉伸量较大时难以收敛。另有学者尝试建立金属丝网套的均质化本构，Hachemi等[8]在非线性正交异性层合板本构中引入了编织角变化，以体现网套拉伸过程中的非线性行为，但在拉伸曲线后半段偏差较大。胡牧原等[9]进一步引入了基于试验数据的编织角加速系数以增强刚度非线性。

本文以网套补偿器这一复杂工程元件为研究对象，通过简化钢丝网套模型，使用仿真方法研究了网套的轴向刚度特性。建立了基于接触关系的补偿器有限元仿真模型，实现了对网套补偿器轴向拉伸全过程的静刚度分析。

1 钢丝网套轴向刚度分析

钢丝网套结构是补偿器轴向刚度特性的非线性来源，也是分析难点。本文建立了网套的简化分析模型——螺旋梁模型，通过有限元仿真方法计算了几何参数对其轴向刚度特性的影响，研究了边界条件对螺旋梁轴向刚度的影响。

1.1 网套简化分析模型——螺旋梁模型

1.1.1 螺旋梁模型简介

网套轴向变形时由于轴向对称性和反对称性，其中钢丝的响应在统计意义上是相同的，因此在轴向变形计算时，可以以单根钢丝为分析对象。网套的细观编织结构使得钢丝的路径比较复杂，难以用简单的数学公式描述。若忽略钢丝的卷曲，则钢丝的路径可简化为螺旋线(见图1)，使分析难度大大降低。

图1 螺旋梁模型示意图Fig.1 Spiral beam model of wire cloth

简化之后，钢丝的路径几何由中心线的螺旋角α0、金属丝螺旋直径D0、网套轴向长度l0这3个几何参数确定。对于由N锭、每锭m根钢丝编织而成的网套，其轴向刚度Kz可由单根钢丝轴向刚度Ks叠加得到

Kz=mNKs

(1)

使用空间梁单元建立螺旋梁仿真模型，对其进行轴向(图1中z方向)变形响应分析。作为分析算例的网套规格见表1。

表1 网套参数表Tab.1 Mesh sleeve parameters

1.1.2 螺旋梁模型可靠性验证与误差修正

采用文献[10]中管状编织结构几何建模方法建立表1中钢丝网套的编织单胞仿真模型(见图2)，分别对内部无约束工况及内部具有刚性芯工况下螺旋梁模型和单胞模型进行仿真分析，以验证螺旋梁模型在模拟网套单独拉伸及与内部芯轴接触时与单胞模型的误差。

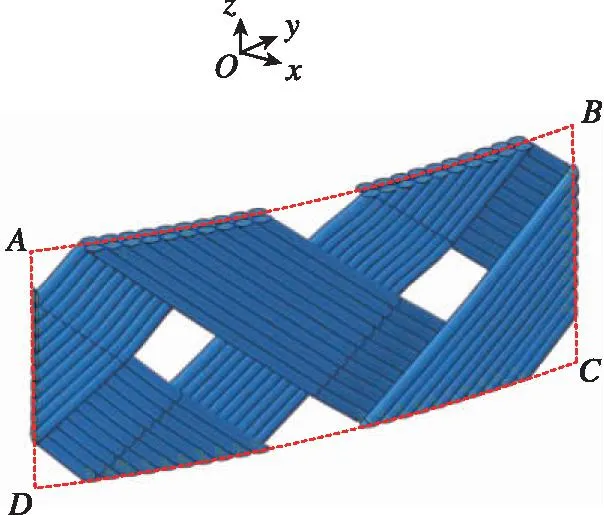
图2 钢丝网套编织单胞仿真模型Fig.2 Simulation model of steel wire mesh sleeve unit cell

用两种仿真模型得到的两种工况下网套轴向拉伸的力-位移曲线见图3。

(a)无内部约束

由图3及表2可知，网套单独拉伸时螺旋梁模型得到的轴向刚度结果和编织单胞差别较小；而在内部有刚性芯时，螺旋梁得到的刚度要显著大于编织单胞，此时有必要对螺旋梁进行修正，以使其轴向刚度与编织单胞相等。本文采用将螺旋角从α0修正至γ0的方式使其轴向刚度与编织单胞等效，按照此方式在内部有芯轴时，表1中网套的编织角由48°增大至52.857°。

表2 钢丝网套轴向刚度仿真结果对比Tab.2 Comparisons of axial stiffness simulation results of steel wire mesh sleeve

1.2 几何参数对轴向刚度的影响

1.2.1 轴向长度l0

螺旋角α0、网套直径D0以及钢丝直径d与表1中网套相同，建立不同轴向长度l0的螺旋梁有限元仿真模型。工程实际中的网套边缘通常使用边条焊接固定，在轴向变形时两端径向、环向以及转动自由度都被固定，只存在轴向位移。因此仿真时螺旋梁端点边界位移和转角条件如下

Ur|A=Ur|B=0
Uθ|A=Uθ|B=0
Uz|A=0,Uz|B=Wz
URr|A=URr|B=0
URθ|A=URθ|B=0
URz|A=URz|B=0

(2)

仿真获得的力-应变曲线见图4。曲线图表明，不同长度的螺旋梁在轴向拉伸时力-应变曲线差别十分明显。相同轴向应变的情况下，螺旋梁的初始轴向长度越长轴向力越小，即其刚度与轴向长度l0之间并非线性关系。

图4 不同轴向长度下螺旋梁轴向拉伸力-应变仿真曲线Fig.4 Axial tensile stress-strain simulation curves of helical beams with different axial lengths

对于特定长度的螺旋梁，其拉伸曲线在弹性范围内随着轴向应变增大，曲线斜率也随之升高。这由几何非线性导致，拉伸过程中梁的大变形(见图5)影响了刚度。轴向长度较短的螺旋梁(如l0=7.5 mm时的曲线)在较大轴向力范围内刚度变化较小，轴向长度较长的螺旋梁(如l0=27.5 mm和l0=30 mm时的曲线)在较大的应变范围内刚度变化也较小。而轴向长度适中的螺旋梁具有最显著的几何非线性。

图5 l0=30 mm螺旋梁拉伸变形位移云图(结果经柱坐标系下z轴旋转阵列展示)Fig.5 Spiral beam tensile deformation displacement nephogram with l0=30 mm(the results are displayed by z-axis rotation array in cylindrical coordinate system)

从仿真结果中提取轴向应变为0.001时的轴向反力，拟合初始的小变形范围内的轴向刚度(见图6)。由图6可知，螺旋梁处于较小轴向长度的范围时，刚度对轴向长度较为敏感，此时刚度随初始长度增加而急剧减小；螺旋梁的初始轴向长度较大时，轴向刚度极低，并且刚度随长度增加而减小的趋势也放缓。

图6 螺旋梁初始轴向拉伸刚度与轴向长度的关系Fig.6 Relationship between initial axial tensile stiffness and axial length of spiral beam

通过提取螺旋梁变形时的应变能仿真值可以解释造成上述现象的原因。在螺旋梁中总的应变能中由拉伸变形贡献的应变能可表示为

(3)

其中，L为螺旋梁的总弧长，εN为沿梁的中心线切向应变，σN为沿梁的中心线切向应力。

由弯曲、扭转和剪切变形贡献的应变能则为

EM=Etotal-EN

(4)

对于Euler-Bernoulli梁，计算时忽略了剪切变形，因此只存在拉伸应变能和弯扭应变能。从仿真结果提取的各轴向长度下，螺旋梁内拉伸应变能与总应变能的比值见图6中的红色虚线，可见拉伸应变能占总应变能比例越高，螺旋梁的轴向刚度也相应越大。这表明螺旋梁刚度随轴向长度的非线性变化主要是内部变形模式的转变导致的。螺旋钢丝轴向长度较大时拉伸变形很小，主要依靠弯扭实现轴向伸长，此时刚度很低。而轴向长度很小时，轴向拉伸时钢丝内主要发生拉伸变形，刚度要高得多。

1.2.2 螺旋角α0

轴向长度l0、网套直径D0以及钢丝直径d与表1中网套相同，建立不同螺旋角α0的螺旋梁仿真分析模型。仿真获得的力-应变曲线如图7所示。曲线图表明，螺旋角越小，螺旋梁轴向刚度越大，同时拉伸曲线越接近线性。

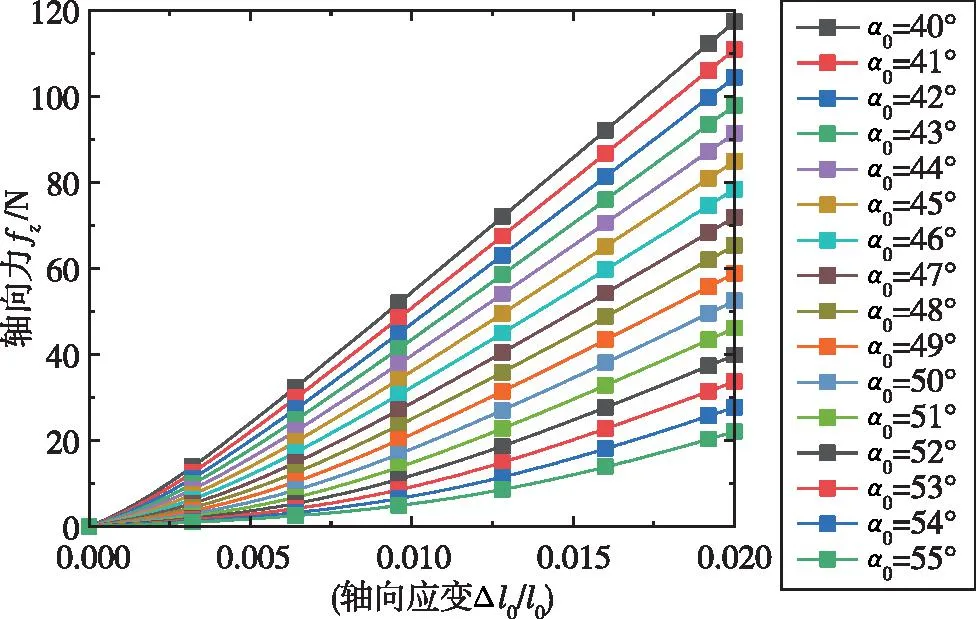
图7 不同螺旋角下螺旋梁轴向拉伸力-应变仿真曲线Fig.7 Simulation curves of axial tensile force strain of spiral beam under different spiral angles

初始的小变形范围内(轴向应变0.001)的轴向刚度仿真值如图8所示。

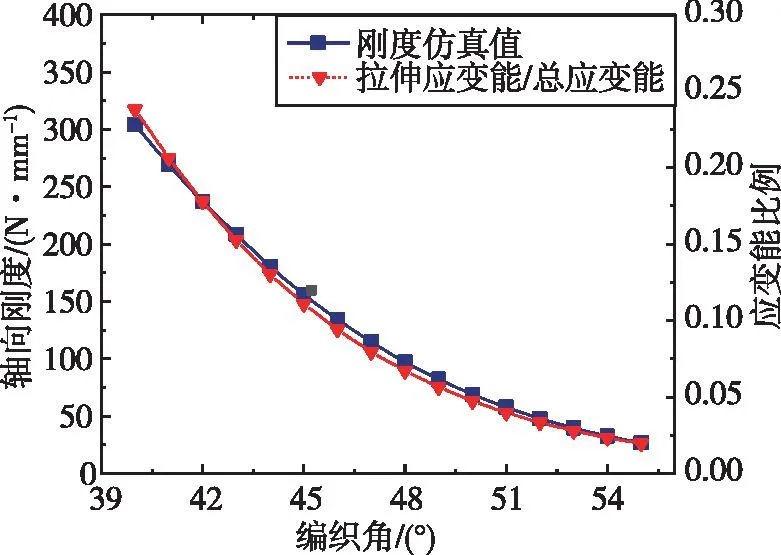
图8 螺旋梁初始轴向拉伸刚度与螺旋角的关系Fig.8 Relationship between initial axial tensile stiffness and helix angle of spiral beam

由图8可知，螺旋梁轴向刚度对初始螺旋角较为敏感，二者之间为非线性变化关系，初始螺旋角越大刚度越低。通过对应变能的计算可以发现，轴向刚度的下降与拉伸应变能比例的下降趋势基本一致，因此螺旋梁刚度随初始编织角非线性变化的主要原因同样是变形模式的转变。

1.2.3 网套直径D0

轴向长度l0、螺旋角α0以及钢丝直径d与表1中网套相同，建立不同网套直径D0的螺旋梁仿真分析模型。仿真获得的力-应变曲线如图9所示。曲线图表明，相对于其他参数，网套直径对螺旋梁轴向刚度影响较小。网套直径越小，螺旋梁轴向刚度越小。

图9 不同直径下螺旋梁轴向拉伸力-应变仿真曲线Fig.9 Axial tensile force strain simulation curves of spiral beam with different diameters

初始的小变形范围内(轴向应变0.001)的轴向刚度仿真值如图10所示。

图10 螺旋梁初始轴向拉伸刚度与网套直径的关系Fig.10 Relationship between initial axial tensile stiffness of spiral beam and diameter of mesh sleeve

由图10可知，螺旋梁轴向刚度随着网套初始直径D0线性变化，刚度随初始直径增大而缓慢升高。对应变能的计算表明，网套直径对拉伸应变能比例影响较小，与对刚度的影响趋势一致。

1.3 边界条件对轴向刚度的影响

1.3.1 固定边界与约束径向位移的循环边界

假设一种理想情形：拉伸轴向长度极大的补偿器时，由于网套的径向收缩效应(见图6)，其中的网套将与波纹管接触。波纹管的表面形状复杂，如果波纹管的刚性很大，则此时网套相当于受到周期性的径向约束，约束周期如图11中AB段所示。

图11 网套受波纹管周期性径向约束示意图Fig.11 Schematic diagram of periodic radial constraint of the mesh sleeve by the bellows

将上述问题进一步理想化为一根无限长度的螺旋梁受到周期性的径向位移约束。在一个约束周期内，梁的两个截面应满足循环边界条件，以使截面处的内力和变形满足连续性。在计算螺旋梁z方向拉伸响应时，循环边界条件要求端点满足如下约束方程

Ur|A-Ur|B=0
Uθ|A-Uθ|B=0
Uz|A-Uz|B=Wz
URr|A-URr|B=0
URθ|A-URθ|B=0
URz|A-URz|B=0

(5)

其中下标A，B分别代表梁的两个端点(见图1)。

由于端点的转动自由度未被完全约束，循环边界下的螺旋梁所受约束要弱于固定边界，因此结构刚度应该不大于固定边界下的螺旋梁。这里对不同轴向长度l0的螺旋梁仿真模型施加约束径向位移的循环边界，并将仿真结果与之前固定边界下的仿真结果进行对比。不同边界下仿真获得的力-应变曲线如图12所示。

图12 不同边界条件下螺旋梁轴向拉伸仿真力-应变曲线Fig.12 Axial tensile simulation force strain curves of spiral beam under different boundary conditions

仿真结果显示，对于不同轴向长度的网套，循环边界和固定边界下的差别都极小。在初始变形阶段，两种边界的力-应变曲线基本重合，只有在大变形时，曲线才略微有差别。这表明在计算螺旋梁轴向刚度时这两种边界条件可以互换，而不会对精度产生影响。

1.3.2 径向位移不完全约束

现实中与网套连接或发生接触的不可能是完全的刚体，弹性体之间的接触将沿接触面法向发生一定量的位移。考虑到这一点，在螺旋梁拉伸仿真时在两端同步施加不同比例的径向收缩位移，以模拟螺旋梁与不同弹性体作用后对轴向刚度的影响。

建立螺旋梁仿真分析模型，轴向长度l0、螺旋角α0、网套直径D0以及钢丝直径d都与表1中网套相同。计算时轴向位移载荷相同，设置不同的径向位移(其值为负)。在不同的径向收缩量下的轴向拉伸仿真结果对比如图13所示。

(a)仿真力-应变曲线

由图13可见，径向收缩量越大轴向刚度越小，相对于几何参数的影响效果，端点径向收缩量对螺旋梁整体轴向刚度径向位移的影响较小。

2 补偿器轴向刚度分析

补偿器的轴向刚度特性表现出高度非线性，本研究基于螺旋梁模型，提出了基于接触关系的子网套刚度分析方法。在子网套分析方法的基础上，建立了适用于不同轴向拉伸阶段的螺旋梁-波纹管模型，同时给出了低刚度阶段和高刚度阶段的补偿器刚度理论估计方法。

2.1 补偿器试验轴向刚度特性

王亚军等[2]对网套补偿器的轴向刚度特性进行了实验研究，文献中试验件1在无内压状态下的轴向拉伸曲线如图14所示。

图14 补偿器轴向拉伸试验曲线Fig.14 Compensator axial curves of tensile test

图14中曲线表现出显著的非线性特征，可划分为3个阶段。

1)低刚度阶段：在拉伸初始阶段刚度近似为常值，力-位移曲线近似为线性；

2)过渡阶段：拉伸至一定位移后力-位移曲线表现出强烈的非线性，刚度开始加速上升；

3)高刚度阶段：随着补偿器拉伸位移继续增加，刚度增速减缓，力-位移曲线又有回归线性的趋势。

将文献[2]中无内压和充压状态下的补偿器拉伸、压缩力-位移曲线绘于同一图(见图15)中进行对比。由图15可知，对于未充压状态下的补偿器压缩，其曲线斜率(刚度)与拉伸的低刚度阶段是相同的。充内压之后补偿器相当于初始施加了一个压力推力，其结果是力-位移曲线发生了平移，但形状基本不变。因此，只要获得补偿器未充压状态下的力-位移曲线，便可以进一步推导得出其余轴向工况下的曲线。

图15 无内压和充压状态下补偿器轴向力-位移曲线Fig.15 Axial force-displacement curves of compensator with/without inner pressure

2.2 基于接触关系的子网套刚度分析方法

补偿器轴向拉伸时表现出的非线性刚度特性由钢丝大变形这一几何非线性过程以及网套和波纹管接触这一边界非线性过程共同导致。结合1.3节中对螺旋梁力学特性的讨论，本文提出了基于接触关系的子网套刚度分析方法，可以综合考虑两种非线性因素。

补偿器松弛状态下网套半径大于波纹管，而受到轴向拉伸时二者将发生接触。当网套与波纹管发生接触之后，截取两波峰之间的网套(见图16)，被截取的网套两端径向位移被波纹管限制，显然该段网套受到的约束程度要比循环边界(图16绿色区域)更强，而比固定边界(图16红色区域)更弱。

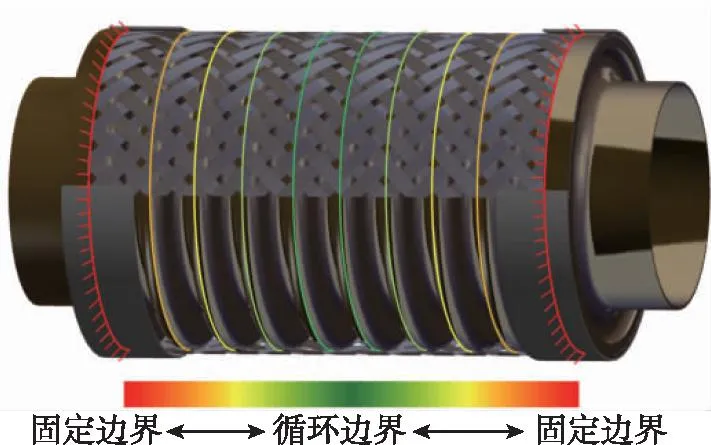
图16 补偿器中的网套分段及对应边界条件Fig.16 Mesh sleeve segmentation and corresponding boundary conditions in compensator

1.3.1节已经证明了在计算螺旋梁模型的轴向刚度时这两种边界条件差别可以忽略，则介于二者之间的真实边界可以用这两种边界来替代。这样就可以将发生接触的网套分段，并将该段网套的边界替代之后，将计算对象缩小为一小段网套，即子网套。

在拉伸初始阶段网套和波纹管之间没有接触，补偿器刚度为二者的轴向刚度叠加，因此试验曲线中该阶段表现为线性。当拉伸到一定量之后，网套和波纹管之间的接触关系使得轴向刚度呈现出强烈的非线性，刚度急剧上升。网套变形和接触区域的变化如图17所示。

图17 网套变形与接触示意图Fig.17 Deformation and contact diagrams of mesh sleeve

接触发生之后，网套中间部分(图17中红色环线)径向位移受到波纹管约束，此时可以把原网套视作两个长度只有原来一半的子网套；随着轴向拉伸量的增大，波纹管接触区域由中间向两边扩展，网套被进一步拆分为更多轴向长度与波距相同的很短的网套(中间段子网套)，以及末端两个稍长的网套(边缘段子网套)。

设波纹管与网套相接触的波数为n，显然整体网套的轴向力Fz、位移Wz与各子网套之间有如下关系

Fd=Fc=Fz
2Wd+nWc=Wz

(6)

其中，下标d表示边缘段子网套对应的物理量，下标c表示中间段子网套对应的物理量。

则网套整体轴向刚度Kz可表示为

(7)

根据式(7)，在拉伸的初始阶段，n=0，Kz=Kd，需要计算的只有单个边缘段子网套(网套本身)。当网套和波纹管接触之后，n逐渐变大，根据1.2.1节中轴向长度对刚度的影响，Kd随轴向长度不断变短而急剧上升，此时刚度Kc基本不变，网套整体刚度急剧非线性上升，这一过程中边界非线性是刚度变化的主要因素。当接触区域不再变化，即网套与波纹管稳定接触之后，n和边缘段子网套初始长度不再改变，但刚度Kd和刚度Kc受几何变形影响而增大，网套整体刚度仍在缓慢上升，此时影响网套刚度的只有几何非线性因素。

2.3 低刚度阶段的补偿器轴向刚度分析方法

在低刚度阶段网套与波纹管无接触，补偿器刚度等于二者的线性叠加。网套对应螺旋梁的轴向刚度以及波纹管的轴向刚度可通过有限元仿真获得，使用的模型与过渡阶段相同，下文详述。

2.4 过渡阶段的补偿器轴向刚度分析方法

过渡阶段网套和波纹管之间的相互作用力水平较弱，此阶段网套刚度的剧烈增加由网套接触区域变化导致，分析重点为接触关系变化过程。本文通过建立2/N波纹管-螺旋梁复合有限元仿真模型，结合插值获得了该阶段补偿器的轴向力-位移曲线。

建立波纹管2/N(N仍表示网套钢丝锭数)模型(见图18)及单根钢丝螺旋梁模型，并在波纹管环向边界处施加循环边界条件。模型中螺旋梁使用实体单元，波纹管使用壳单元。螺旋梁和波纹管之间设置无摩擦“硬”接触，对波纹管和螺旋梁两端面施加相同的轴向位移。

图18 2/N波纹管-螺旋梁复合模型Fig.18 2/N bellows with spiral beam composite model

根据1.1.2节，补偿器在网套与波纹管接触前采用未修正螺旋角的螺旋梁模型计算误差较小，在网套与波纹管完全接触之后，应该使用修正过螺旋角的螺旋梁。分别建立螺旋角为α0和γ0的2/N波纹管-螺旋梁复合模型(后文简称α0模型和γ0模型)。从有限元结果中提取螺旋梁和2/N波纹管的位移及反力结果，按如下关系进行叠加可得补偿器整体轴向刚度K

(8)

其中，Kb为2/N波纹管的轴向刚度；式中右侧第一项为钢丝网套的整体轴向刚度，第二项为整个波纹管的轴向刚度。

在接触过程中过渡阶段的拉伸曲线，可以基于α0模型和γ0模型的仿真数据进行插值获得，插值方法如下。

设α0模型得到的仿真位移-力曲线函数关系为x1=f1(y)，γ0模型得到的仿真位移-力曲线函数关系为x2=f2(y)。α0仿真模型钢丝和波纹管开始接触时为插值起点，此时轴向拉力值为a；γ0仿真模型接触波数不再变动为插值终点，此时轴向拉力值为b。构造插值函数x=p(y)，插值函数需满足

p(a)=f1(a)
p(b)=f2(b)

(9)

按以上条件可构造插值公式

(10)

最终由式(10)获得的y=p-1(x)即为该阶段补偿器拉伸响应的力-位移关系。

需要指出的是，α0模型显然可以得到接触发生之前补偿器的拉伸曲线，即低刚度阶段曲线，只需将接触发生之前的螺旋梁和2/N波纹管的仿真结果代入式(8)即可。

2.5 高刚度阶段的补偿器轴向刚度分析方法

补偿器拉伸到一定位移后，网套和波纹管接触关系达到稳定，力-位移曲线进入高刚度阶段，可以按2.2节中的网套分段方法分别对边缘段子网套和中间段子网套进行仿真分析。

2.5.1 边缘段子网套

使用三结点二次空间梁单元建立边缘段子网套的螺旋梁模型。边缘段子网套两端边界更接近固定边界(见图16)，故在仿真计算时对螺旋梁两端施加固定边界条件。

2.5.2 中间段子网套

进入高刚度阶段后，中间段子网套与波纹管相互作用较为强烈。考虑到波纹管径向弹性变形将对网套刚度产生影响，本研究在仿真建模时，中间段子网套与边缘段子网套使用了不同的建模方法。对应的螺旋梁两端施加循环边界，并且建立了波纹管模型，以体现二者的相互作用。

中间段子网套对应的分析对象为两端施加循环边界条件且与两波峰接触的螺旋梁，如图19左图所示。左图仿真模型的接触区域被人为地分割，增加了接触状态判断的计算量，使得有限元计算收敛困难。为避免上述问题，在实际计算时波纹管采用图19右图所示单波模型。该模型与所要分析的中间段网套以及对应的波纹管波谷段在几何上不同，但在施加循环边界条件后，经过阵列和旋转操作，都可变换为长度无限的带网套的补偿器，二者描述的是同一整体力学模型的一个周期，故其轴向力学响应是相同的。

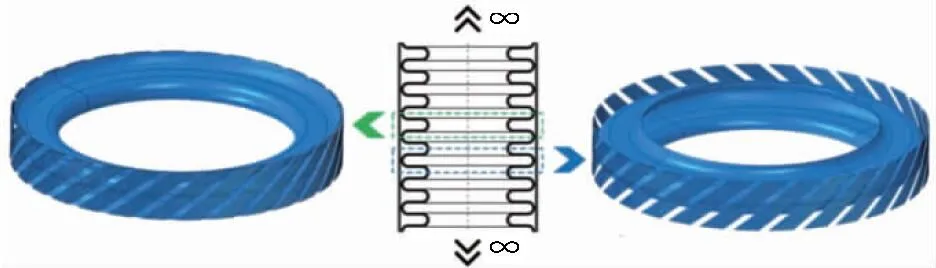
图19 中间段子网套和波纹管模型的等效变换Fig.19 Equivalent transformation of the model of the intermediate sub mesh sleeve and bellows

对于图19所示的仿真模型，可根据环向周期性进一步将模型缩小为原来的2/N(见图20)，只需对波纹管左右边界施加环向周期性条件即可。图20为最终计算中间段子网套轴向响应使用的仿真模型。

图20 2/N单波-单锭螺旋梁复合模型Fig.20 2/N single wave with single spindle spiral beam composite model

复合模型中钢丝使用C3D8R实体单元，波纹管使用S4R壳单元。钢丝和波纹管之间设置无摩擦“硬”接触，对波纹管两端施加轴向位移载荷，同时通过螺旋梁两端面约束的参考点施加相同的轴向位移。

3 算例与结果分析

3.1 补偿器参数

本文以文献[2]中的试验件1为算例，在下文分析补偿器的轴向刚度。其中波纹管的规格如表3所示。

表3 分析所用补偿器中波纹管规格Tab.3 The specifications of bellows in the compensator analyzed

网套参数与表1相同。

3.2 低刚度阶段及过渡阶段计算结果

根据1.1.2节，对于本文研究的起始编织角为48°钢丝网套，对应的螺旋梁在接触波纹管之前α0取48°，与波纹管稳定接触之后γ0取52.9°。

接触发生之前α0模型得到的低刚度阶段仿真力-位移曲线与试验曲线进行对比，见图21。在该阶段仿真值和试验值一致性较好。

图21 低刚度阶段仿真与试验力-位移曲线对比Fig.21 Comparison of force-displacement curves between simulation and test at low stiffness stage

图22给出了仿真模型的接触应力云图，α0模型计算得到钢丝和波纹管开始接触时，轴向位移Wz为0.69 mm；γ0模型计算得到的接触波数不再变动时，轴向位移Wz为2.32 mm。由此可确定过渡阶段的起点和终点。

图22 2/N波纹管-螺旋梁复合模型接触应力云图Fig.22 Contact stress nephogram of 2/N bellows with spiral beam composite model

按式(10)拟合的插值曲线与试验曲线对比如图23所示，二者的一致性较好。由力-位移曲线可知，当补偿器开始拉伸时，试验值与螺旋角为α0模型的仿真值更为接近。当网套与波纹管开始接触之后，α0模型误差逐渐增大，试验曲线向螺旋角γ0模型的仿真曲线靠近。本文提出的基于螺旋梁仿真值的插值方法可有效模拟补偿器过渡阶段的力-位移曲线。

图23 基于仿真结果的过渡阶段插值曲线Fig.23 Interpolation curves in transition phase based on simulation results

3.3 高刚度阶段计算结果

按照子网套分析方法，稳定接触之后需将网套分解为如表4所列的子网套。

表4 子网套参数表Tab.4 Parameters of sub mesh sleeve

将中间段网套及边缘段网套仿真结果按式(8)的关系整合后，与波纹管力-位移曲线叠加，获得高刚度阶段的补偿器仿真力-位移曲线。截取补偿器试验力-位移曲线的高刚度部分(按2.3节中的计算结果为438 N之后的曲线)，其与仿真值对比如图24所示。

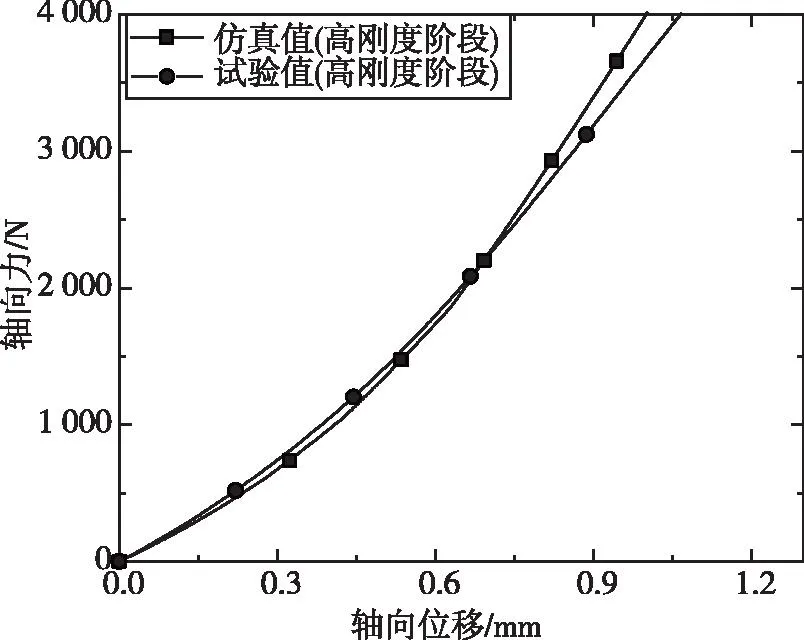
图24 高刚度阶段仿真与试验力-位移曲线对比Fig.24 Comparison of force-displacement curves between simulation and test at low stiffness stage

由图24可见，仿真模型得到的高刚度阶段力-位移曲线呈现弱非线性，与试验结果一致性较好。

表5给出了由试验曲线中高刚度阶段近似线性部分的轴向刚度、仿真曲线近似线性部分的轴向刚度对比。仿真值与试验值偏差较小，由本文提出的高刚度阶段仿真计算方法是可靠的。

表5 高刚度阶段补偿器刚度对比Tab.5 Stiffness comparison of compensator in high stiffness stage

3.4 补偿器轴向计算结果总结

将各阶段仿真曲线相结合，结果如图25所示。

图25 补偿器轴向拉伸全过程力-位移曲线仿真值与试验值Fig.25 Comparison of compensator force-displacement curves between simulation and test in the whole process of axial tension

由图25可知，仿真得到的轴向拉伸全过程力-位移曲线与试验曲线一致性较好，能够复现补偿器的非线性刚度特性，证明了本文提出的补偿器轴向响应分析方法的可靠性。