Robust Distributed Model Predictive Control for Formation Tracking of Nonholonomic Vehicles

Zhigang Luo , Bing Zhu , Jianying Zheng , and Zewei Zheng

Dear Editor,

This letter proposes a robust distributed model predictive control(MPC) strategy for formation tracking of a group of wheeled vehicles subject to constraints and disturbances.Formation control has attracted significant interest because of its applications in searching and exploration [1], [2].The objective of formation tracking is to achieve the reference formation via interactions among agents.In formation tracking, MPC can be applied to treat constrains.In [3], by sharing predictive information with neighbors, each agent uses distributed MPC strategy to generate the desired trajectory without any collision.Based on the leader-follower structure, a distributed MPC is proposed in [4] to mitigate effects caused by replay attacks.In [5],distributed MPC is applied to optimize energy scheduling.

Nonholonomic systems refer to those with non-integrable constraints [6].For wheeled vehicles, side-slip is un-permitted, and this constraint is non-integrable.Besides, control constraints and external disturbance are suggested to be considered in kinematics of nonholonomic systems.A disturbance observer-based MPC strategy is designed in [7] to estimate unknown disturbances.A velocity integral controller incorporated in MPC is proposed in [8] to guarantee the formation control.Two robust MPC strategies are proposed in [9]for a unicycle robot to track its reference trajectory, where the formation with communications is not considered.

Inspired by [9], a robust distributed MPC for formation tracking of the non-holonomic multi-vehicle systems is proposed in this letter.Subject to the input constraint and external bounded disturbances,each vehicle tracks a virtual time-varying trajectory generated by the virtual structure approach, and exchanges information to achieve the formation.Main contributions include: 1) A modified robust constraint is designed to guarantee feasibility in case of bounded disturbances, and a novel positive invariant terminal set and auxiliary control are designed for individual vehicles to guarantee stability; 2)Coupling costs in individual optimizations are proposed for formation tracking.

Problem statement: Consider multi-vehicle systems

Fig.1.Configuration of the virtual leader and followers.

Algorithm 1 Robust Distributed MPC Algorithm for Each Vehicle 1: At the initial time , set and ,send to , and receive from.˜u∗ei(τ|tk),˜u∗i(τ|tk)tk=t0 ˜zi(tk|tk)=zi(tk) ˆpei(τ|t0)=pei(t0|t0)ˆpei(τ|t0) j ∈Ni ˆpej(τ|t0) j ∈Ni 2: Solve the optimization problem of every vehicle in parallel to obtain the optimal virtual error control sequence and calculate the actual control input of each vehicle.u(τ)= ˜u∗i(τ|tk) τ ∈[tk,tk+1)3: Apply to the real system over.ˆpei(τ|tk+1) j ∈Ni ˆpej(τ|tk+1) j ∈Ni 4: Calculate predictive error trajectory and send it to and get from.tk+1=tk+δ 5: Let and go to Step 2.

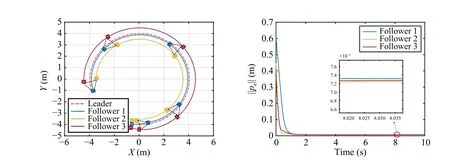
Fig.2.Trajectories of three non-holonomic agents in formation tracking with the proposed robust distributed MPC (left); Norms of tracking errors (right).

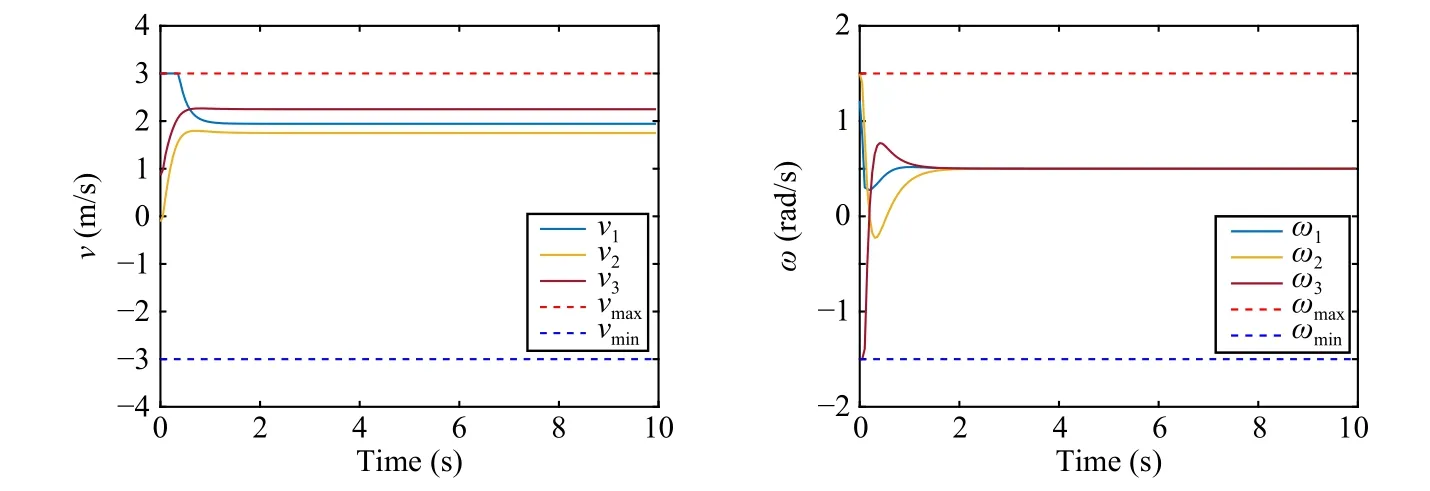
Fig.3.Linear velocities (left) and angular velocities (right).

It is shown in Fig.2 that three followers reach the desired positions and keep a fixed configuration.Norms of tracking errors are shown in Fig.2, where tracking errors converge to the neighborhood of the origin.Control inputs are displayed in Fig.3.It can be judged that, with the proposed robust distributed MPC, formation tracking is achieved with satisfactory performance, and no constraints are violated in presence of bounded disturbance.Admittedly, the theoretical bound of tolerated disturbance is small due to conservative calculation.

Conclusion: A distributed robust MPC is designed for formation tracking of nonholonomic systems with input constraints and bounded disturbances.A robust constraint is presented to resist the external disturbances.Coupling costs are constructed to keep agents in formation.Theoretical proof and simulation example show that the recursive feasibility is ensured, and tracking errors are stabilized within a robust invariant region.

Acknowledgments: This work was supported by the National Natural Science Foundation of China (62073015, 62173016).