Reinforcement Learning in Process Industries:Review and Perspective

Oguzhan Dogru , Junyao Xie ,,, Om Prakash , Ranjith Chiplunkar , Jansen Soesanto ,Hongtian Chen ,,, Kirubakaran Velswamy , Fadi Ibrahim , and Biao Huang ,,

Abstract—This survey paper provides a review and perspective on intermediate and advanced reinforcement learning (RL)techniques in process industries.It offers a holistic approach by covering all levels of the process control hierarchy.The survey paper presents a comprehensive overview of RL algorithms,including fundamental concepts like Markov decision processes and different approaches to RL, such as value-based, policybased, and actor-critic methods, while also discussing the relationship between classical control and RL.It further reviews the wide-ranging applications of RL in process industries, such as soft sensors, low-level control, high-level control, distributed process control, fault detection and fault tolerant control, optimization,planning, scheduling, and supply chain.The survey paper discusses the limitations and advantages, trends and new applications, and opportunities and future prospects for RL in process industries.Moreover, it highlights the need for a holistic approach in complex systems due to the growing importance of digitalization in the process industries.

I.INTRODUCTION

REINFORCEMENT learning (RL) has emerged as an effective tool for solving complex decision-making problems in a wide range of fields.It has sparked a growing interest in the process industries in recent years, where it has shown promise in optimizing processes, increasing efficiency,and improving safety [1].Testing RL in simulated environments, laboratory experiments and pilot-scale setups has yielded significant outcomes and brought RL closer to realworld applications.As a result of these outcomes and rapid developments in computational technologies, numerous technology organizations have created and supported various research institutes to accelerate RL research in robotics and language models.Despite these advancements outside process industries, most of the RL methodologies use a combination of learning and process control techniques extensively studied in the optimization and control of process industries[2].On the other hand, operational drifts and varying dynamics of processes require modifications in classical techniques and more sophisticated and adaptable solutions.In order to understand and contribute to RL theory in process industries while improving its applicability in real-time, researchers and practitioners should analyze the operational levels in process control holistically [3].A systematic outline for these levels(the control hierarchy), was initially given in [4] without considering possible faults in the production, supervision and execution levels.Fig.1 generalizes the existing presentation of the control hierarchy by considering complex applications in the real world, and this study provides representative RL applications for each level.

Despite RL’s potential in the control hierarchy, its methodologies face several challenges, including a lack of high-quality data for training, simultaneous learning and control in realtime, interconnectivity and complexity of systems.Moreover,optimal control strategies depend on industries, and finding them through RL involves high risk and cost due to significant trial and error and long-term effects.Nonetheless, it has been reported that several RL methods can solve real-world problems effectively.

Parallel to the ongoing process control and automation research, Industry 5.0 builds upon Industry 4.0, aiming toovercome its limitations and prioritize human-machine interaction.Process control, automation, and reinforcement learning are crucial for achieving the goals of Industry 5.0.For example, network automation, a key aspect of Industry 4.0,has supported large-scale Industrial Internet-of-Things (IIoT)and optimized service quality while reducing complexity and cost [5].However, Industry 5.0 introduces new challenges like cross-layer network optimization and privacy/security protection.Reinforcement learning can address these challenges by enabling comprehensive network optimization and enhancing privacy/security measures.Industry 5.0 also emphasizes societal significance and a human-oriented approach beyond production efficiency and economic goals.SCADA systems have evolved with concepts like event-oriented, data-driven, and model-driven systems.Reinforcement learning can enhance these systems by providing intelligent decision-making capabilities and adaptive control that align with human needs.Supply chain management has transitioned from Supply Chain 4.0 to Supply Chain 5.0, focusing on tailored demand fulfillment and better human-machine relationships.Reinforcement learning is crucial in optimizing supply chain processes, improving demand forecasting, and facilitating effective human-machine collaboration.In summary, reinforcement learning complements process control, automation, and the advancements of Industry 5.0.It enables comprehensive network optimization,adaptive control in SCADA systems, and improved supply chain management.By learning from data and making intelligent decisions, reinforcement learning facilitates humanmachine interaction, resilience, sustainability, and societal value in Industry 5.0 [6].

TABLE I NOMENCLATURE

Some studies reviewed machine learning and RL applications in specific domains, including supply chain management [7], process control [8], fault detection and diagnosis [9],[10], etc.However, there is still a lack of a comprehensive review of the state-of-the-art theory, outstanding challenges in the unified control hierarchy, and possible improvements for practical solutions beyond toy problems and small-scale implementations.A detailed analysis of the methodological development of RL techniques, concerns and obstacles, and future prospects may help researchers and practitioners implement, enhance, and expand the existing accomplishments more rigorously.As a result, the main contributions of this manuscript are to show the developments in deep learning,process control, and RL, introduce advanced RL techniques,present an overview of the recent progress in RL in process industries, and discuss the future prospects in a compact manner.Table I presents the abbreviations used in this manuscript.

The manuscript is organized as follows.Section II progressively introduces the motivation behind RL in process industries, Section III mathematically explores the RL theory, Section IV reviews the recent literature with a focus on soft sensor design, process control, fault detection and diagnosis, fault tolerant control, optimization, planning, scheduling, and supply chain management.Then, Section V discusses the outstanding problems and possible extensions that researchers and professionals of process industries can consider.

Research Methodology: In order to compile the specific literature as extensively as possible, this survey focuses on the relevant keywords in the control hierarchy shown in Fig.1.An example combination is as follows [“Process control” OR“Fault detection”] AND [“Reinforcement learning”].After filtering the literature in Google Scholar, Web of Science, Scopus, and IEEE Xplore using these keywords, this article includes peer-reviewed research and review papers written in English.In order to focus on the most recent developments,the survey paper considers the articles published after January 2019 in most of the survey sections (e.g., in process control).However, since this is the first review article that focuses on the entire control hierarchy, it also considers older articles in sections like automated soft sensor design and fault detection.Moreover, to minimize the overlap and provide a unique resource, the articles covered in the recent related review papers (e.g., in [11], [12]) were excluded from this survey’s scope.Fig.2 presents the number of related articles in the Scopus database to highlight the importance and opportunities in these fields.

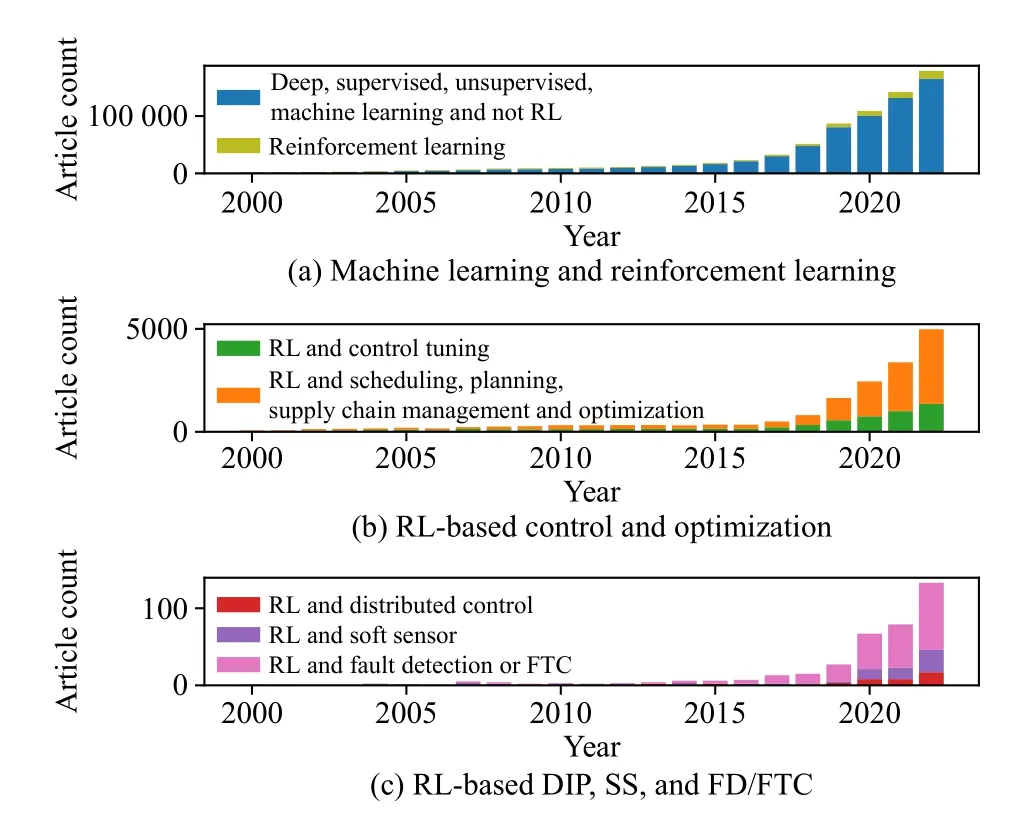
Fig.2.Scopus literature survey for the related topics.The figure shows an exponential increase in the topics covered in this survey paper since 2000.

II.RECENT INNOVATIONS IN CONTROL AND LEARNING TECHNOLOGIES

A. Advances in Process Control

Process control is a highly interdisciplinary field that has been evolving from the earliest forms of proportional-integralderivative (PID) controllers to the more sophisticated optimal control schemes.While the PID controllers are effective for low-level, simpler control tasks (execution level in Fig.1), the optimal control schemes are preferred for complex systems,particularly at the supervisory level.The general optimal control problem is formulated as a cost-minimization problem expressed as follows:

where Φ0,ζ, and Φτrepresent the arrival, running, and terminal costs respectively.Variablesxandurepresent the states and inputs, respectively.The linear quadratic regulator (LQR)and the model predictive controller (MPC) are the most popular optimal control scheme where the cost functions are taken as quadratic functions.The LQR usually solves the optimization problem once in the selected window, whereas the MPC solves the optimization problem in a receding window manner at every time instant.Moreover, LQR assumes a linear model, while the MPC framework can handle both linear and nonlinear system models.Thus, MPC is more widely used as it is more suitable for real process systems.Optimal control schemes, in general, are very versatile and have the ability to incorporate various system complexities.

One such complexity arises from the fact that modern processes are highly integrated.This leads to complex systems that contain multiple sub-systems which interact with each other.Distributed MPC techniques have been explored in the past couple of decades [13] for such systems.Economic MPC is another widely explored category of MPC that combines the economic objectives of a plant operation with the control objectives [14].This fuses the production-level decisions and supervisory-level controls depicted in Fig.1, thus leading to a holistic consideration of various aspects such as economics,time-varying operation, and process dynamics.Robust MPC is another important area that has received substantial attention.This deals with the issues such as model mismatch, uncertainty in the system model, and the presence of unknown disturbances.Some important methods include tube-based MPC[15], stochastic MPC [16], etc.

The standard MPC formulations usually assume the availability of a process model which may be challenging to develop for complex systems.Thus, the recent trend has been implementing MPC based on data-driven techniques for learning system dynamics or controller design [17].In particular,increasing focus is on approaches that do not learn an explicit parametric model using system identification techniques.Thus, MPC implementations based on approaches such as Gaussian process models [18], direct utilization of historical signal trajectories [19], etc., have been explored.The advent of deep learning has also resulted in the adoption of deep learning into optimal control problems.There has been considerable research on using neural network architectures in MPC for various objectives such as learning the feedback control law [20], and modelling process dynamics [21].In particular, dynamic network architectures such as recurrent neural networks (RNN), long short-term memory (LSTM), and gated recurrent units (GRU) are commonly used to model process dynamics.

B. Advances in Deep Learning

The modern resurgence in deep learning started in 2006 with works related to greedy layer-wise training using restricted Boltzmann machines [22].Since then, deep learning has been continuously evolving both in terms of training methods and architectures.The improvements in the training methods include weight initialization, weight regularization,dropout, etc.[23].Similarly, the architectural improvements have also been significant.Several breakthrough architectures since 2006 include the generative adversarial network, GRU,variational auto-encoder (VAE), residual network, and attention-based neural networks [24].These developments have vastly improved the fields of computer vision, natural language processing, finance, engineering, etc.Deep learning has also been finding wide acceptance in process industries owing to its ability to model complex nonlinear systems.Deep learning and machine learning, in general, can be broadly classified into three categories: unsupervised learning, supervised learning, and RL.All three facets of deep learning have been utilized in process industries, particularly the unsupervised and supervised learning techniques, which have been extensively explored.

1)Unsupervised Learning: Unsupervised learning has been used in process industries for a variety of process monitoring applications, such as fault detection and diagnosis [25], and fault prognosis [26].Since modern industrial processes are complex in nature, a deep learning approach is a suitable choice for these tasks.Similar to the general deep learning research, the research for process industrial applications also has been evolving continuously to accommodate more complex structures.These include auto-encoders, GANs, VAE,RNN, and their variants [27], [28], etc.This array of methods spans a wide range of approaches covering the aspects of deterministic and probabilistic methods, and dynamic and static methods.Recently, RL has been explored as an avenue to achieve these traditional unsupervised learning tasks.

2)Supervised Learning: As with unsupervised learning,there is extensive research in deep learning for supervised learning applications in process industries.In the process industries, supervised learning is primarily used for tasks such as soft sensing [29] and fault classification.Architectures such as the stacked auto-encoders, LSTM, and, VAE [30], [31]have been explored to achieve these tasks.Besides these traditional nonlinear regression-type tasks, computer vision-based soft sensors also have been developed [32], which rely on CNN to extract essential features from an image for supervised learning.

Both the unsupervised and supervised learning techniques are usually purely data-based and require a vast amount of data to obtain reliable models.RL, on the other hand, is a learning framework where an agent interacts with the system and gets a reward for achieving a certain goal [33].The agent learns the system information in this process and develops a decision framework to achieve the goals.RL thus can aid the traditional supervised and unsupervised learning tasks where even with the vast amount of data, one still has to manage certain aspects such as the selection of features, selection of network architecture, and dealing with unseen data, etc.Thus,apart from the control applications, RL may also be used to aid the conventional unsupervised and supervised learning tasks in process industries.

C. Advances in Reinforcement Learning

Parallel to the advancements in control and DL, RL has advanced over the past decade, primarily driven by the research institutions supported by the technology industry.Primary developments include but are not limited to the following:

1)Stabilityin policy and value function updates [34], [35],which can improve the learning in actor-critic settings,

2)Sample efficient explorationandmodel-basedlearning that can speed up learning without requiring lengthy or costly operations [36], [37],

3) Interactive RL that utilizeshuman feedbackto improve agent’s behaviour based on expert knowledge [38].

Although these topics will not be covered in this context,this survey paper will provide insights about leveraging these techniques in process industries.Despite specific advancements in the RL literature (e.g., robust RL, model-based RL,offline RL, etc.), the RL in this article refers to generic online model-free RL, unless otherwise specified.More details about algorithmic improvements in RL have been listed in [39].

D. Relationship Between Classical Control and RL

The theoretical foundations of RL and optimal control originated from the 1950s with dynamic programming (DP).Despite this crucial fact, they were studied separately between the late 1900s and 2010s.For example, the computational science community has focused primarily on the learning stability and sample efficiency of the algorithms on toy problems,while the process industries’ main concern was control stability in complex systems.However, learning and control performance often affect each other and should be analyzed jointly.This section connects RL and classical control (specifically MPC) to motivate the necessity of such joint developments.The broad similarities between the two approaches are due to the fact that the stochastic MPC and RL essentially solve the same or a similar objective function.Stochastic MPC minimizes the expected value of the cost function given in (1),while RL maximizes the expected value of a reward function as will be discussed in Section III-A.On the other hand, RL and classical MPC methodologies differ due to several reasons:

1) Most RL methodologies utilize episodic learning,whereas MPC focuses on continual calculations.

2) Model-free RL [33] uses an explicit model only during training and can operate without a model after training.In contrast, MPC always requires a model.

3) General MPC often utilizes a quadratic or linear objective function.This function is used to track a setpoint, reject disturbances, or enhance control stability and smoothness.On the other hand, RL uses a more general reward function that is customized to the particular application.This reward function can be discrete or continuous.As a result, the optimizers that MPC and RL use can differ significantly.Numerous training and evaluation objectives for RL applications will be provided in Table III.

4) MPC does not typically take an adaptive form, while RL adapts to environmental changes.

5) RL often uses an approximated function to represent the policy, which can describe complex control structures, while MPC relies on a mathematical model, which is less flexible.

The following section discusses the fundamentals of RL to explain these similarities and differences mathematically.

III.REINFORCEMENT LEARNING PARADIGMS AND ALGORITHMS

Unlike MPCs, which control systems using process models directly, machine learning methods require training a neural network based on process data.That is, the data used in MPC is the current feedback from the system, which is an estimate of the state of interest.Although a conventional time-invariant MPC provides a locally optimal controller output at each step, it does not handle variations in the operational conditions since it does not have an update mechanism.

Inspired by model-based dynamic programming [40] and animal learning, RL provides an alternative framework to optimal control by training an agent in the process environment [33].The agent optimizes a control policy while interacting with the environment.The policy defines the behaviour of the agent given a state during the interaction.After an action is selected according to the policy, it is implemented in the environment, and the agent receives a reward signal, indicating the goodness of the decision.Although the agent can learn a policy offline (through historical data) [41], this section will cover online/recursive RL algorithms that can learn autonomously without explicit system knowledge or any process model.

This section is divided into four subsections, each explaining a different RL element.Section III-A introduces the concept of Markov decision process (MDP), which is a formalization of sequential decision-making and forms the mathematical foundation of RL.Section III-B presents values-based RL where actions are selected based on their estimated action values.Section III-C highlights policy gradient RL, where the agent directly learns a parameterized policy to select actions.Finally, Section III-D covers various actor-critic-based methods that are also policy-based RL, but they consist of two parameterized functions that work together to select actions.

A. Markov Decision Process

Sequential problems require optimal decisions with temporal order.Considering the complex nature of the environment,the outcomes of the actions of an agent are often uncertain.The MDP is a probabilistic framework for sequential decisionmaking where the agent observes a state,x∈X, chooses an actionu∈U, and receives a reward,r, and the next state,x′∈X.This framework assumes the Markov property, where the information in the next time step depends only on the current time step, as shown in Fig.3.A transition probability function,p(x′,r|x,u), governs the system dynamics.The agent aims to maximize a return function,G, shown in (2).

where the capital letters denote that the reward is a stochastic variable,tindicates discrete time steps, and γ ∈[0,1] is a weight that controls how much future gains will contribute to the return function.During its interactions with the environment, the agent samples its actions from a stochastic policy,π(u|x), the performance of which is tracked using a value function.There are two kinds of value functions:v(x) andq(x,u), and the type depends on the policy evaluation approach.Learning can be performed by solving the Bellman equations iteratively, as illustrated in (3) and (4) [42].

Fig.3.A graphical representation of the Markov decision process.The next state and the reward depend only on the current state and action.The capital letters indicate that the state, action and reward are random variables.

where E [·] represents the expected value of a random variable.Equations (5) and (6) can be used to find the optimal value functions after the recursions.

Finally, (7) can be used to calculate the optimum (also known as greedy) policy.

However, because the system model,p(·), is often unknown, (3) and (4) cannot be solved analytically.To tackle this problem, the agent learns a value (or a policy) function from the data and stores it in memory, whereas, for example,the MPC iteratively optimizes the value function at each step using the system model.

B. Value-Based RL

Initial RL implementations used the value-based (criticonly) methodology [43] to obtain an optimal policy and solve control problems.In these methodologies, actions are derived directly from a value function, which predicts the long-term outcomes of a specific policy.The state value function (shown in (3)) is the expected return obtained from statexwhile following policyπ.The action-value function (shown in (4)) is the expected return after taking actionuin statexand following the policyπthereafter.The optimal value functions,v∗(·)andq∗(·) (shown in (5) and (6)) are the unique value functions that maximize the value of every state.

Value-based methodologies, during policy evaluation, estimateV(x)≈vπ(x) orQ(x,u)≈qπ(x,u) for the current policy and improve the policy iteratively.A common example is greedily selecting actions with respect to the updated value function.

Although dynamic programming (DP) [40] and Monte Carlo (MC) techniques can be used to solve an RL problem,these methods are computationally infeasible, need to wait until an episode ends, have high variance, or require a perfect system model.Temporal difference (TD) methodology provides a practical alternative to these algorithms by combining the bootstrapping (estimating the values by using the previously estimated values) ability of DP and the model-free nature of MC.As a result, TD algorithms can update their policies before an episode ends.Two examples of TD-based state and action-value function update rules are given in (8)and (9).

where “ ←” represents the update operation, where(Rt+1+γV(Xt+1)) andV(Xt) in TD learning respectively correspond to measurement and prediction in classical control.

Built upon the TD learning methodology, two RL algorithms, namely SARSA (state-action-reward-state-action) and Q-learning [33], have shown promising results in process control applications [11].These algorithms differ in terms of their policy evaluation/improvement strategies.For example, SARSA is anon-policyalgorithm since it improves a policy that is used to make decisions.In contrast, the Q-learning algorithm isoff-policysince it improves a policy different from that used to generate data.The policy improvement step is given by(10).This step shows that the SARSA algorithm uses the next action,Ut+1, in the process and updates the Q-function, as shown in (9).However, the Q-learning algorithm performs an additional greedy action selection to findUand updates the action-value (Q) function by usingU, as shown in (10).

SinceUis not used to control the system (but is used to update the Q-function), it can act as an additional exploration factor in Q-learning.On the other hand, the optimal Q-function can result in aggressive control actions, which can compromise safety, as Sutton and Barto showed [33] through a cliff walking problem.Therefore, the practitioners must select and test the appropriate algorithm considering mathematical and safety requirements.

The terminal state in RL can be defined based on an event or time for process industries.Some examples of the terminal state include but are not limited to an “unsafe” state (e.g.,when the simulated temperature of a hydrocracking reactor reaches 10 000 K), a physically impossible state (e.g., in a simulated environment, when the temperature reaches -1 K), a specific time step (e.g., when the plant has been operated for ten hours), and average return value (e.g., when the agent has achieved an integral absolute error of 100 bar).If the hyperparameters are selected appropriately, SARSA and Q-learning algorithms will asymptotically converge to their optimal values [33].Successful SARSA and Q-learning applications have been reported in [44], [45].

A challenge with SARSA and Q-learning algorithms is that the action value function is stored as a look-up table, where the Q-value is represented explicitly for each state-action pair.On one hand, large discretization steps can reduce the accuracy of the Q-table.However, selecting small discretization steps makes it infeasible to store and update the Q-table for large or continuous state/action spaces.Therefore, for large state/action spaces, a practical solution is to use approximate value functions, such asV(x|ω) orQ(x,u|ω), instead of storingv(x) for each state value orq(x,u) for each state-action pair.The parameters of the value functions are specified byωin this case.A variety of applications have utilized deep neural networks to train RL agents in large/continuous state spaces [46], [47].Nevertheless, the value-based RL algorithms often generate discrete and deterministic actions(which can be insufficient for continuous state-action space control problems) and have been reported to be divergent for large-scale problems [48].

C. Policy-Based RL

Process industries often involve large/continuous action spaces with stochastic state transitions.Policy-based (actor-only)methods [49], [50] learn stochastic and continuous actions by parameterizing a policy, πθ(u|x,θ), and directly optimizing it by using a performance metric, as demonstrated in (11).

whereJ2(θ) is the agent’s objective function, andθrepresents the policy weights.As stated in (12), the policy update rule can be obtained by using the policy gradient theorem [33].

whereαdenotes the learning rate.Although policy gradient methods can converge to at least locally optimal policies,learn continuous actions and “fuzzy” strategies that are a mixture of different actions, and often converge better than the value-based methods, they generally suffer from higher variance than the value-based methods.To reduce the variability during learning, REINFORCE algorithm modifies the policy gradient algorithm as shown in (13) [51].

whereb(Xt) is a baseline independent on the action,Ut.Suttonet al.[52] have modified this methodology further by replacing the actual return with the action value function,qπ(Xt,Ut)as shown in (14).

Although (12) and (13) updateθin the direction of high return values,αandGtremain crucial forθto converge.For example, an indication of convergence is Δθ →0 [52].However, this convergence condition may not be satisfied if|Gt|＞ξ or |∇lnπ|＞ξ, withξbeing a small threshold value,which can result in non-convergence.Nevertheless, the definition of convergence depends on the application.Moreover,Qπin (14) is the expected return, which is initially unknown and can take a long time for the agent to learn it.Despite these challenges, policy-gradient methods have been applied to continuous action spaces in various domains.

D. Actor-Critic RL

Similar to a student-teacher pair or generative adversarial networks (GANs) [53] that utilize generative and discriminative networks, actor-critic algorithms generate control actions and examine the outcomes by using a scalar reward signal without any labels [54].As shown in Fig.4, these algorithms combine policy and value-based methods via an actor and a critic, respectively.The actor and the critic can be represented as two neural networks, π(u|x,θ) andV(x|ω) (orQ(x,u|ω)),respectively.This value-assisted policy learning methodology reducesθvariability while promoting convergence to optimal policies [33], [55].Although various actor-critic algorithms have been proposed to solve the optimal control/RL problems,an early example combines the policy gradient with statevalue estimation [33], as shown in (15).

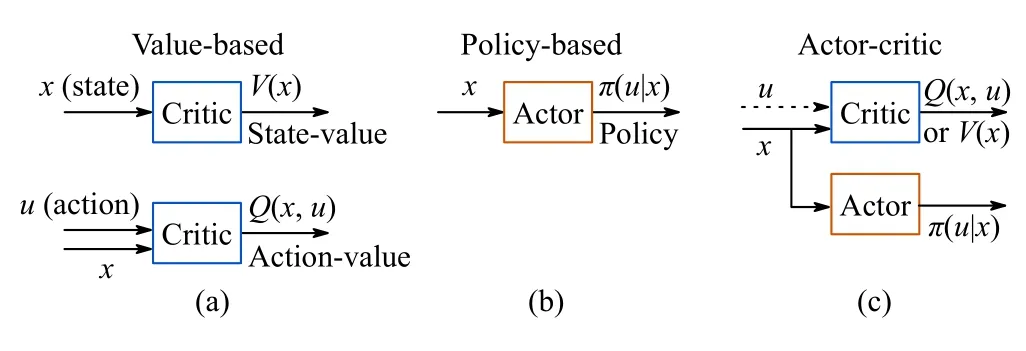
Fig.4.Comparison of value, policy and actor-critic based RL.The valuebased methods derive the policy based on the value functions (which estimate the future return values), the policy-based methods directly optimize the policy, and the actor-critic methods simultaneously learn the policy and the value functions.

Initially,V(Xt,ω)≠(Rt+1+γV(Xt+1,ω)) sinceωis often a set of randomly initialized parameters.As a result, high values of (Rt+1+γV(Xt+1,ω)) will result in large Δθ.However, asV(Xt,ω) approaches (Rt+1+γV(Xt+1,ω)), the variability inθdecreases over time [56].

This subsection focuses on the most commonly used modelfree algorithms that are represented in Table II.Some of these methods use entropy regularization, whereas others take advantage of heuristic methods.A common example of these methods is theε-greedy approach, where the agent takes a random action with a probability ε ∈[0,1).ε=1 corresponds to random search since it learns a policy but does not utilize the learned policy in the decision-making process.Other exploration techniques include but are not limited to introducing additive noise to the action space, introducing noise to the parameter space, utilizing the upper confidence bound, etc.The readers can see [11] for more detail.The actor-critic algorithms are summarized as follows:

1)Deep Deterministic Policy Gradient(DDPG): The DDPG algorithm [57] has been proposed to generalize discrete, low-dimensional value-based approaches [62] to contin-uous action spaces.This algorithm uses two deep neural networks, namely the deep policy gradient (DPG) and deep Qlearning algorithms, to map the states into actions and estimate the action-value function (Q-function), respectively.The resulting architecture is shown in Fig.5.

TABLE II A COMPARISON OF THE ACTOR-CRITIC ALGORITHMS BASED ON THE TYPE OF ACTION SPACES & THE EXPLORATION METHOD.THE STATE SPACE CAN BE EITHER DISCRETE OR CONTINUOUS FOR ALL ALGORITHMS

Fig.5.A schematic of the DDPG algorithm.The solid lines show the data flow, and the dashed lines show the update mechanism.

Similar to the policy update methodology shown in (15),this algorithm updates the policy by using the derivative of the Q-function with respect toω.This update rule helps the agent maximize the expected return while improving the value estimation and policy.In addition to this improvement, this algorithm utilizes copies of the actor (π (u|x,θ) and critic(Q(x,u|ω)) as target networks (π (u|x,θ′)Q(x,u,ω′)).After observing a state, real-valued actions are sampled from the actor-network and are mixed with a random process (e.g.,Ornstein-Uhlenbeck process, [63]) to encourage exploration as shown in (16).

whereOUis the Ornstein-Uhlenbeck process,dOU=-(OUη)OUdt+σdWt,OUη＞0 and σ ＞0 are tuning parameters, andWtis the Wiener process with d representing the ordinary differential symbol.Note that theOUprocess is a correlated noise, but the use of white noise has also been reported for exploration purposes [61].The agent stores state,action, and reward samples in an experience replay buffer to break the correlation between consecutive samples to improve learning.It minimizes the mean square error of the loss function to optimize its critic, as shown (for one sample) in (17),and updates the policy parameters using the policy gradient shown in (18).

The target networks are updated using a low-pass filter, as shown in (19).

where τddpgis the filter coefficient that adjusts the contribution of the observation (ωandθ, which are a function of the empirical/observed reward) and the previous values of the target parameters.Since the value function is learned for the target policy based on a different behaviour policy, DDPG is an off-policy method.

2)Asynchronous Advantage Actor-Critic(A2C/A3C):Instead of storing the experience in a replay buffer that requires memory, this scheme involves local workers that interact with their environments and update a global network asynchronously, as shown in Fig.6.This update scheme inherently increases exploration since the individual experience of the local workers is independent [56].Instead of minimizing the error based on the Q function, this scheme minimizes the mean square error of the advantage function (Aorδ)for critic update, as shown in (20).

Fig.6.Multiple worker scheme in the A3C algorithm.Local workers interact with their environment and update a global network.Using a single A3C worker results in an A2C agent.

In this scheme, the global critic is updated by using (21) and the entropy of the policy is used as a regularizer in the actor loss function to increase exploration, as shown below:

where initiallydθG=dωG=0.αcand αaare the learning rates for critic and actor, respectively, andβis a fixed entropy term that is used to encourage exploration.SubscriptsLandGstand for the local and the global networks respectively.Multiple workers (A3C) can be used in an off-line manner and the scheme can be reduced to a single worker (A2C) to be implemented online.Even though the workers are independent, they predict the value function based on the behaviour policy of the global network, which makes A3C an on-policy method.

3)Actor-Critic With Experience Replay(ACER): ACER was proposed to address sample inefficiency of A3C and improve learning stability [36].The algorithm utilizes ‘truncated importance sampling with bias correction, trust region policy optimization, stochastic “duelling” network architectures, and the Retrace algorithm [64].the ACER algorithm modifies the policy update rule shown in (15) for a trajectory{X0,U0,R1, µ(·|X0),...Xk,Uk,Rk+1, µ(·|Xk)}and calculates

the importance weighted policy shown in (23).

where the truncated importance weight, η¯t=min{c,ρt}, andcis a clipping constant.The algorithm updates the actor and critic using the clipped trust region policy optimization technique and the Retrace algorithm shown below：

wherefrepresents a sampling distribution,φis a neural network that generates the statistics off,, andDKLis the KL divergence.Because of its Retrace algorithm,ACER is an off-policy method.

4)Proximal Policy Optimization(PPO): The trust region policy optimization (TRPO) algorithm suggests maximizing a soft-constrained objective function shown in (30),

whereβis a weight for the KL divergence term, and θoldrepresents the old policy parameters.Atis the advantage estimate that represents how good the agent’s actions are, as shown in(20), and the KL divergence creates a lower bound on the performance ofπ.However, using a fixed weight,β, in the objective function shown in (30), can result in large policy updates.To avoid abrupt changes in the policy, the PPO algorithm suggests [58] clipping the surrogate objective function as shown in (31).

wherec1andc2are weight coefficients,H =.The resulting architecture of the PPO algorithm is shown in Fig.7.Due to the practical advantages of these modifications, PPO and its variants have been one of the most commonly used algorithms to solve control problems [65].

Fig.7.A schematic of the PPO algorithm.The solid lines show the data flow, and the dashed lines show the update mechanism.

5)Actor-Critic Using Kronecker-Factored Trust Region(ACKTR): Classical gradient descent/ascent algorithms, such as the general policy gradient algorithm (shown in (15)),update the parameters by solving the optimization function shown in (33).

whereF=Ep(τ)[∇θlogπ(Ut|Xt,θ)(∇θlogπ(Ut|Xt,θ))T], andτis shown in (35).

wherepdenotes the probability distribution functions.As a result of these improvements, ACKTR has shown successful results in various applications [67].

6)Soft Actor-Critic(SAC): Unlike methods such as A3C and PPO, which use the entropy of the policy as a loss regularizer [56], [58], [68], SAC augments the reward function with the entropy term (as shown in (36)) to encourage exploration while maintaining learning stability.

whereθrepresents the parameters of the policy, andαis a user-defined (fixed or time-varying) weight to adjust the contribution of the entropy, H.This scheme relies on bothQ(·,φ)andV(·,ω) functions to utilize the soft-policy iteration.The parameters of the neural networks are updated, as shown in(37)-(39).

whereUtisevaluated atfθ(ϵ|Xt),ϵisanoise vector,andQˆ(Xt,Ut)=Rt+1+γEXt+1[Vω′(Xt+1)].Similar to DDPGand PPO, SAC stores the transitions in a replay buffer, indicated as D, to address sample efficiency.This approach has also been reported in [55], [60] to improve the robustness of the policy against model and estimation errors.Besides enhancing the exploration, this off-policy training methodology has been used in several control and optimization applications[69] and reported to improve stability since it utilizes target networks.

7)Twin Delayed Deep Deterministic Policy Gradient(TD3): TD3 is an extension to the DDPG algorithm [61].It addresses error propagation (which is a non-trivial challenge in statistics and control) due to function approximation and bootstrapping (i.e., instead of an exact value, using an estimated value in the update step).To reduce the overestimation bias, the scheme predicts two separate action-value functions and prefers the pessimistic value to update the network parameters, avoiding sub-optimal policies.TD3 utilizes target networks, delays the update to the policy function, and uses an average target value estimate by samplingN-transitions from a replay buffer to reduce variance during learning.The scheme introduces exploration by adding Gaussian noise to the sampled actions and performs policy updates using the deterministic policy gradient [49].As a result of these modifications,TD3 has been considered one of the state-of-the-art RL algorithms in control and optimization [70], [71].

IV.RL APPLICATIONS IN PROCESS INDUSTRIES

Now that various RL algorithms have reviewed, this section presents applications of RL in various activities relevant to process industries.

A. Soft Sensors

Soft sensors, also known as inferential or virtual sensors, are widely used for quality estimation, process monitoring, and feedback control [29].When building a data-driven soft sensor model, there are mainly four procedures, including data selection, model selection, model training and validation, and model maintenance.Typically, data-driven soft sensor models individually consider the aforementioned modelling procedures and process knowledge is applied to each procedure separately and in a non-autonomous manner.Moreover, most existing data-driven soft sensor methods are based on traditional statistical methods and/or (semi) supervised learning methods that eventually lead to specific regression modelling problems.

Compared to traditional statistical methods and/or (semi)supervised machine learning-based data-driven soft sensor methods, RL enables autonomous soft sensor design.Thanks to the nature of the MDP, RL can be naturally applied to address dynamic soft sensor design problems.The crucial aspects of soft sensor modelling tasks, including data selection and regression model training, validation, and maintenance, may be addressed as a sequential decision-making problem via RL.Recently, one interesting work proposed a framework based on deep RL for autonomous data selection and soft sensor modelling [72], where the authors formulated the soft sensor as an MDP problem and showed that the proposed RL methods outperform some commonly utilized datadriven soft sensor methods, including statistical methods,transfer learning methods, and just-in-time learning methods.Reinforcement learning and particle filtering were jointly used in [73] for remaining useful life estimation of sensor-monitored degrading systems.In addition, [74] suggested using soft sensing techniques for quality prediction and data collection in RL-based control optimization of wastewater treatment processes.To the best of the authors’ knowledge, the research results in this direction are very limited.The applications of RL in autonomous soft sensing deserve future research.

B. Process Control

As motivated in Fig.1, the primary process control (after instrumentation and monitoring) occurs in the Execution and Supervision levels, where the controllers drive the controlled variables to the desired operating points.Successful RL implementations can cater to maintaining safe, optimal and environmentally-friendly operations if these desired points are optimally determined and if the controller parameters are selected appropriately.This section divides process control into two levels.Low-level control refers to the controllers at the Execution level (e.g., PID, LQR, and MPC), high-level control refers to tuning these controllers’ hyperparameters(e.g., PID parameters, MPC parameters).

1)Low-Level Control: Classical control theory has limitations in achieving complex desired behaviours, even with variants of the quadratic cost function.To address this, the model predictive control (MPC) cost function can be automatically learned through inverse reinforcement learning (IRL).This method could particularly be useful for large-scale systems with intricate interactions, as demonstrated in [75].

Traditional controllers depend on accurate system models to achieve optimal performance, which may not always be available.In contrast, RL offers more adaptable and versatile solutions.In [76], RL and MPC were combined to create an optimal controller that addresses safety and stability issues in linear systems.The resulting controller provides better adaptability and reliability than traditional approaches.

Safety is a crucial consideration when implementing RL agents, especially in process industries where operational variables are critical.State constraints can be added to the RL learning objective to maintain safety, as shown in [77].Additionally, input constraints proposed in [78] can promote operational safety by limiting the actions of the RL agent.

Additionally, it was demonstrated that multi-agent RL systems could be trained to control multiloop processes in a feedforward feedback configuration to promote closed-loop stability and disturbance rejection, which can significantly enhance control performance [79].However, the potential benefits of multi-agent RL systems come with the cost of potentially time-consuming training processes.Despite this, the benefits of multi-agent RL systems in promoting closed-loop stability and disturbance rejection make them a promising area of research for researchers in process control and process automation.

Another promising approach for heating, ventilation, and air conditioning (HVAC) system control combined deep learning and MPC to utilize the benefits of modern and classical control techniques [80].This algorithm effectively improves system performance by assigning the update target as the cumulative reward in the prediction horizon of MPC.The proposed method has been validated through a case study involving a two-zone data center in a simulated environment, where it achieves the largest average rewards with four weather data sets out of five.These results demonstrate the potential for this approach to enhance HVAC system performance, making it a valuable addition to the toolkit of process industries.

A novel RL-based approximate optimal control method that guarantees state-constraint handling abilities on attitude forbidden zones and angular velocity limits has been proposed in[81].In this work, barrier functions were used to encode constraint information into the cost function, and a simplified critic-only neural network was used to replace the conventional actor-critic structure.The authors also demonstrated promising estimation error given limited excitation instead of persistent excitation.The effectiveness and advantages of the proposed controller were verified by numerical simulations and experimental tests.

In addition to these developments in the low-level control settings, the controller performance often depends on parameter tuning, also known as high-level control, as will be discussed in the following subsection.

2)High-Level Control: A meta-RL approach to tuning fixed structure controllers in closed-loop without explicit system identification has been presented in [82].It was shown that the proposed algorithm was able to tune fixed-structure process controllers online with no process-specific training and no process model.Despite this algorithm’s incremental nature,which can result in divergent control performance, the authors proved the concept of control tuning using meta-learning schemes.

Another model-free goal-based algorithm for self-tuning MIMO PID systems for real-time mobile robots has been presented in [83].The proposed adaptive architecture allows for a direct representation of the state space, and the network used for parameterizing the policy function is able to directly output the parameters of the MIMO system without any reparameterization.

In addition, a contextual bandit-based approach for PID tuning has been proposed in [84] to handle parameter-varying and nonlinear systems.This approach first trains an agent on a step response model to address sample efficiency and then fine-tunes the agent to learn the model-plant mismatch online.This type of learning can benefit industries with thousands of PID loops where the systems cannot be excited persistently.

An automated tuning framework for the weights of nonlinear MPC to reduce the time and effort of users has been proposed in [85].The proposed agent was implemented in two stages.In the first stage, the agent explored the weights that could maintain the vehicle position at the desired points.In the second stage, the agent was trained to find the best parameters for trajectory tracking.The empirical results validated computational efficiency, direct applicability, and satisfactory trajectory tracking performance.Therefore, this two-step methodology can be helpful for practical implementations in process industries that involve setpoint tracking problems.Similarly, a dynamic weights-varying MPC was developed to autonomously learn a policy for online weight modifications of an MPC cost function [86].This approach used deep RL and allowed users to specify additional objectives in a multiobjective cascaded Gaussian reward function.The agent observed the low-level states and their deviations from their setpoints while outputting the controller weight parameters.Empirical findings showed that the proposed methodology outperformed a manually-tuned MPC.In addition to the weights of controllers, finding appropriate lengths of prediction and control horizons is challenging.It was demonstrated that for simple systems, RL could be used to automatically modify and adapt the prediction horizon of the MPC controllers using only a few minutes of data collection [87].These tuning methods have shown that RL could be used for autonomous controller optimization.

C. Distributed Industrial Processes and Control

Distributed industrial processes, also known as distributed parameter systems, are often considered another major class of industrial processes in addition to lumped parameter industrial processes.Compared to lumped parameter processes modelled by ordinary differential equations (ODE), as covered in the earlier sections, distributed parameter processes are modelled by partial differential equations (PDE) or partial integral-differential equations (PIDE), which makes them capable of describing spatial-temporal dynamics in numerous industrial applications, e.g., processes that involve chemical reactions, heat transfer, crystal growth, or irrigation, fluid dynamic and flexible mechanical systems (e.g., flexible aircraft wing design) utilize PDEs and PIDEs to describe the system dynamics comprehensively [88].However, due to the complexity of PDE (or PIDE) models, applications of RL in distributed parameter processes are more challenging and complex than that in ODE-based processes from both theoretical and practical viewpoints.

Over the past decades, various contributions have been reported in the literature on RL-based control synthesis of distributed parameter systems.An adaptive-critic-based optimal neuro control strategy was proposed for distributed parameter systems in [89], where an approximate discrete dynamic programming was used for the problem formulation, and necessary conditions of optimality were derived.By using proper orthogonal decomposition and approximate dynamic programming, a single-network-adaptive-critic scheme was designed(as a stabilizing state-feedback controller) to control the heave dynamics of a flexible aircraft wing in [90].Based on the empirical eigenfunctions (computed from the Karhunen-Loeve decomposition method) and neural networks, approximate optimal controller designs were considered for dissipative PDE systems [91] and one-dimensional parabolic PDE systems [92].Apart from optimal control designs, various RLbased methods have been applied to address other types of control problems, including an off-policy RL method developed for the data-drivenH∞control in [93], a convolutional RL framework proposed for distributed stabilizing feedback controller design in [94], an off-policy integral RL algorithm proposed for dealing with the nonzero-sum game in [95], and so on.Recently, a network-based policy gradient RL algorithm (i.e., the proximal policy optimization) was compared with the Lyapunov-based controllers in a traffic PDE system[96], and the RL controller showed compatible performance with the Lyapunov-based controllers, especially in learning(i.e., adaptation) potential under changing and uncertain conditions while the training time was long and convergence of the value function was not guaranteed.Moreover, a value-iteration-based RL method was proposed for sensor placement in the spatial domain of distributed parameter systems in [97].Most aforementioned methods first lump distributed parameter systems (with infinite-dimensional state spaces) into lumped parameter systems (with finite-dimension state spaces) via various reduced-order models and then perform the RL-based control designs.This implies that these RLbased PDE control designs often depend on specific approximation schemes and lead to approximate control laws [98].The direct RL-based control design on PDE systems constitutes future work.

D. Fault Detection and Fault-Tolerant Control

This section examines reinforcement learning (RL) algorithms used to address fault detection (FD) and fault-tolerant control (FTC) problems.The primary objective of FD is to detect faults and determine their source promptly.FTC is designed to enable the system to persistently function in the presence of failures while maintaining a minimum level of performance.In such cases, the system may operate at a reduced capacity compared to a fault-free scenario.

1)RL-Based Fault Detection: Research on RL-based FD can be mainly divided into model-based and data-driven approaches [99], [100]:

a) Model-based RL FD methods rely heavily on accurate mathematical modelling knowledge [10].As part of this approach, diagnostic models are constructed to analyze the system output and compare the state of the machine in terms of health [9], [101], [102].This approach is derived from the traditional fault diagnosis.

b) The data-driven approach directly applies deep RL techniques for encapsulated processing of the acquired signals to output fault identification results, as shown in references[103], [104].This “end-to-end” approach directly realizes the output from input to target, promoting the joint optimization of feature extraction and pattern classification parameters in multi-hidden-layer networks.This approach also adopts a strategy of self-learning to automatically discover effective features associated with the target in large datasets.

2)RL-Based Fault-Tolerant Control: Fault tolerant control(FTC) has been widely developed to improve the performance of industrial systems in the face of unexpected faults,accidental events, and aging components.RL has emerged as a novel approach for FTC, offering the advantage of requiring fewer design efforts compared to traditional model-based and learning-based methods.By using powerful neural networks and self-adjusted methods, RL-based strategies can effectively address problems such as disturbance elimination, reference tracking, and fault tolerance [105], [106].In addition, RL provides a feasible method for learning in unknown environments with a large amount of prior data, making it a promising approach for FTC in complex industrial systems.Recent studies have reported successful results in RL-based FTC,including FTC tracking control of MIMO discrete-time systems [107], [108], FTC design for a class of nonlinear MIMO discrete-time systems [109], [110], and RL-based FTC for linear discrete-time dynamic systems [111], [112].These promising findings suggest that RL-based FTC can significantly benefit industrial systems, and further research in this area should be encouraged.To motivate a novel FTC perspective, the following example illustrates the principle of linear model-based FTC.Taking a linear time-invariant (LTI) system as an example, a fault results in the difference (donated asSF(z)) between the nominal plant and the faulty counterpart.Then, a separate control structure can be equivalently described whereQr(z) is a filter to be tuned by using RL.IfSFdoes not affect the system stability, tuningQr(z) is sufficient to tolerate the unpredictable faults.

Besides these advancements and possible improvement areas, it is challenging to implement RL in FTC due to the need for a large amount of training data.This lack of effective training data presents a significant hurdle for RL-based methods, making it challenging to design real-time agents that can handle unforeseen faults.Another challenge to implementing these algorithms is the high false-positive alarm rates.Overcoming these challenges is critical for successfully implementing RL-based FD and FTC, which can improve system performance and reduce downtime.Therefore, developing novel training acceleration methods to mitigate the impact of errors and improve training efficiency is a worthwhile research direction for RL-based FD and FTC.

E. Optimization

The hierarchical nature of industrial processes involving multiple decision-making levels, such as process design, planning, scheduling, and supply chain, presents challenges in coordinating decisions within each level.Traditionally, these problems were modelled as MILP or MINLP that are NP-hard[113] and are solved using computationally expensive optimization techniques such as Branch and bound and cutting plane methods [114].

RL has recently attracted attention to this domain as its utilization in industrial process optimization offers several advantages.First, industrial processes are inherently complex,making the implementation of model-based optimization challenging [115].Whereas RL algorithms learn the process behaviour and optimal actions through continuous interaction with the environment, eliminating the need for a process model.Moreover, RL can learn from model mismatches and compensate for them in their actions, leading to improved decision-making [116].Additionally, in time-critical industrial processes, fast optimization is crucial for timely decisionmaking [117].RL offers the advantage of training an optimal policy instead of optimizing actions at every time step.Once the optimal policy is found, an inexpensive forward pass through the function can instantly generate an online solution,leading to faster decision-making.Hierarchical or multi-agent RL has also gained attention for its ability to model complex systems and optimize decisions at different levels of the production process.Applying hierarchical RL to hierarchical and combinatorial optimization problems can simplify the largescale optimization problem into smaller, more tractable subproblems, leading to improved efficiency and effectiveness[118].Moreover, the design of RL allows for the incorporation of relevant information related to decision-making that may be hard to model in traditional optimization techniques,providing flexibility in capturing important process dynamics.Process systems engineering (PSE) communities have been contributing to solving some of the decision-making problems.A literature review on a specific application of RL in supply chain management can be found in [7].Further,Table III lists some significant RL applications in this domain.

In terms of future work, providing any optimality guarantee to RL-based solutions is an open problem.Also, there is an opportunity to combine RL with conventional optimization approaches to leverage the advantages of both techniques.

V.DISCUSSION

Besides these developments in process industries, the RL literature is evolving rapidly in various fields.To acceleratethis expansion safely and realistically, researchers and practitioners should consider RL’s advantages, limitations, and opportunities while examining the trends and new applications.This section discusses these crucial topics to guide the reader.

TABLE III RL APPLICATIONS IN PROCESS OPTIMIZATION, PLANNING AND SCHEDULING

A. Limitations and Advantages

The concept of autonomy tries to decipher decision-making,especially during adverse situations.The nature of such situations is both sparse and sporadic in nature.Such scenarios are usually based on plants’ apparent behaviours unique to each site/unit operation.Such sparse events and adverse interactions have led to potential loss of production and, in the worst cases, fatal injuries.Combined with the nature of the scenarios as well as their sparsity of occurrence, no standard operating procedures can streamline the experience an operator may have in suitable countermeasures developed over time.

While a multitude of models, such as soft sensors, estimators, and forecasting, have been successfully developed and deployed, their usage is limited to normal operations.Fault tolerance or prevention is rarely inherently a part of their design.Such a modal approach to the machine learning models and their poor adoption of sparse scenarios renders them impractical in capturing the operator’s instincts.This impracticality is mainly owing to the fact that these models are mostly spatial, limiting them in understanding the long-term implications of a decision.This segues into an opportunity to understand the long-term impact of certain decisions.A time-tested approach for plant optimization is to utilize model predictive controllers to provide appropriate decisions considering the states/measurements from the unit operation.These methods heavily rely on the plant dynamics that are ever-changing and nonlinear in standard templates.The challenges in linearization as well as the heavily invasive approach of plant perturbations, limit this approach to depend on plant inertia.These issues render the inherent characters in the plant, which otherwise are available in the plant data, useless.

RL, as a tool to identify and understand operator instincts,can ensure the preservation of operator instincts, which otherwise would be lost with the personnel over time.The approach involves the utilization of the RL platform to develop a data-driven approach to understanding the longterm implications of operator decisions.The approach can be realized in two steps.The first is an imitation learning-based approach, which aims at exploiting the operator experience using a one-to-one map of decisions from operator data.This approach would allow the RL agent to comprehend the spatial nature of the decisions.During this scenario, if an actor-critic setup is utilized, the value of such decisions can also be empirically assessed, and the critic can be calibrated.The second and crucial step is to deploy the RL agent into an exploration phase.Here, the decisions can be provided to the operators as recommendations.These recommendations can be constrained/flagged/validated by the operator.Based on the number of times the operator accepts the decision, further deliberation of such learning platforms can be commenced.Operator intuition being a crucial part of industrial autonomy, RL provides a robust platform for learning such sparse information.

B. Trends and New Applications

Classical control theory often utilizes an average cost function as shown in (1).On the other hand, most of the RL implementations utilize episodic learning even if they are finally used for continual processes.Since the optimal policies in episodic problems can significantly differ in continual processes, an emerging research topic iscontinual learning[127].In this setting, the agent/learner utilizes non-discounted variables, similar to the classical-control-theoretic applications.Moreover,safe learningtechniques showed promising results in the robotics and control fields [84], [128].These techniques update the actor and critic functions based on the parameter and system constraints.In addition to these advancements, multi-agent methodologies [129] and agents that utilize human feedback to improve their policies [130]can speed up learning and improve exploration and interpretability of the control system by incorporating human expertise and knowledge.This interaction can also help overcome data availability limitations and uncertainty in the process by incorporating the intuition and experience of human operators.Overall, applying RL in complex process industries can lead to more efficient, reliable, and sustainable processes with improved performance and reduced operational costs.

C. Opportunities and Future Prospects

1)RL Applications in Educational Settings: The relative recency of using RL in real-life applications, particularly in process industries/engineering, created a need for qualified engineers equipped with such ML expertise typically not covered by the engineering curriculum.Only computer science departments teach RL and deliver qualified computer scientists to join the demanding market.However, using ML tools in the process industry requires targeted knowledge in specific engineering domains.Hence, engineers and expertdomain matters are more suited to use RL theory and tailor it for every application independently.Therefore, engineering students should be educated and trained with RL to apply it in process industries.However, teaching such specialized and advanced ML tools (RL) in the classroom without pedagogical applications has been considered a challenge, and some experimental applications were proposed in [131].

2)Fault Detection,Tolerance,and Recovery: Industrial fault recovery is crucial for the safe and reliable operation of systems.While this survey presents promising RL-based approaches for fault detection and tolerant control, there is a need for resilient agents to recover from unsafe operations.For example, a malfunctioning sensor or actuator in a chemical plant can lead to catastrophic accidents.Designing an RLbased fault recovery agent that adjusts parameters, reroutes flows, or safely shuts down systems can greatly benefit plant operations.By leveraging RL’s ability to learn and make intelligent decisions, these agents enhance reliability and safety in Industry 5.0.Future research should focus on effective RL fault recovery strategies, considering interconnected components and potential cascading effects.Integrating RL into fault recovery achieves greater fault tolerance, ensuring continued operation, minimizing unexpected events, enhancing system reliability, and promoting safe human-machine collaboration in Industry 5.0.

3)Complex Systems and Holistic Designs: This survey has identified that previous research has predominantly focused on using RL to improve individual levels in the control hierarchy, as shown in Fig.1.However, this approach fails to consider the interconnectedness of multiple levels in most process industries, which can significantly impact the overall performance of the control system.To address this issue, future research should focus on developing advanced RL algorithms that can optimize the control system design by considering the interactions between multiple levels of the process control hierarchy.Moreover, integrating reinforcement learning into Industry 5.0 holds immense potential for advancing process control and automation.New evaluation metrics and benchmarks should be developed to assess the performance of algorithms in more realistic and complex industrial settings.Pursuing these research directions can improve process control systems’ efficiency, reliability, and sustainability and enable the transition toward autonomous and intelligent manufacturing.

4)Autonomous Control Systems: Designing sequential interactions in the control hierarchy can be complex and challenging.Due to limited considerations, the traditional approach of using programmable logic controllers (PLCs) may compromise process optimality and safety.To address this, a better alternative is to define higher-level objectives and explore various scenarios comprehensively, enhancing both safety and optimality.Implementing hard constraints requires process knowledge and models while incorporating expert information into system identification methodologies leads to successful applications.Data-driven methods face challenges with extensive training time, but this can be mitigated through offline pre-training, model-based RL agents, long historical data, or sparse agents.Smooth transitions during shutdown and startup phases are crucial for handling nonlinear dynamics.Commissioning an autonomous process automation system is a complex task that requires collaboration across disciplines.RL implementations offer an efficient trial-and-error approach, automating the sequence design process, reducing design times, optimizing control system design, and improving process performance with speed and accuracy.This integration of reinforcement learning, autonomous control systems, and Industry 5.0 presents opportunities for advanced process automation, enabling efficient and adaptive control in complex industrial environments.

5)Cyber Attacks: RL can be used to mitigate cyber attacks or enhance cyber security.However, several types of challenges need to be addressed when deploying RL agents.These challenges include the security and privacy challenges of cyber-physical systems, the unpredictability and modelling challenges of human behaviour when mitigating humanrelated vulnerabilities, the challenges of handling system and performance constraints in the learning process, and improving the learning speed.Moreover, non-stationary environments should also be considered in cyber systems.The success of RL algorithms depends heavily on accurate and consistent feedback from the environment.However, such feedback is challenging to guarantee under various cyber attacks,such as denial-of-service (DoS) attacks, jamming attacks,spoofing attacks, data injection attacks, data poisoning attacks,test-item attacks, etc.To understand RL under cyber attacks, it is necessary to understand the attacking behaviours and how specific attacks influence the learning results of RL.For example, designing learning rules requires further design considerations in the presence of cyber attacks.Otherwise, the learning results (e.g., the policy parameters) could be corrupted due to adversaries causing misleading information(e.g., the reward, measurement, and control signals) since a naive agent might not be able to notice the attacks [132]-[134].Although several research articles address adversary detection and mitigation through RL solutions [135]-[137],deploying RL agents in process industries requires further research for robustness and safety [138].