Communication Resource-Efficient Vehicle Platooning Control With Various Spacing Policies

Xiaohua Ge,,, Qing-Long Han,,, Xian-Ming Zhang,,, and Derui Ding,,

Abstract—Platooning represents one of the key features that connected automated vehicles may possess as it allows multiple automated vehicles to be maneuvered cooperatively with small headways on roads.However, a critical challenge in accomplishing automated vehicle platoons is to deal with the effects of intermittent and sporadic vehicle-to-vehicle data transmissions caused by limited wireless communication resources.This paper addresses the co-design problem of dynamic event-triggered communication scheduling and cooperative adaptive cruise control for a convoy of automated vehicles with diverse spacing policies.The central aim is to achieve automated vehicle platooning under various gap references with desired platoon stability and spacing performance requirements, while simultaneously improving communication efficiency.Toward this aim, a dynamic event-triggered scheduling mechanism is developed such that the intervehicle data transmissions are scheduled dynamically and efficiently over time.Then, a tractable co-design criterion on the existence of both the admissible event-driven cooperative adaptive cruise control law and the desired scheduling mechanism is derived.Finally, comparative simulation results are presented to substantiate the effectiveness and merits of the obtained results.

I.INTRODUCTION

THE number of vehicles on roads dramatically grows over the past two decades due to rapid urbanization and growing mobility demands.This poses considerable implications on congestion, safety, parking, and emission of road transport systems [1].Automated vehicle platooning, as a promising intelligent transportation system technology, has attracted intensive research interest owing to its potential benefits, such as driving safety, traffic and fuel efficiency, and emission reduction.

Adaptive cruise control (ACC) is a widely-adopted driverassistance system designed to facilitate road vehicles to keep a safe following distance from vehicles ahead and to alleviate the stress of human drivers from constantly using accelerator and brake pedals.More specifically, with the aid of on-board sensors (e.g., ultrasonic sensor, radar, lidar), an ACCequipped vehicle is capable to detect any vehicle that may be ahead within some specific range, and to measure the relative distance and speed.Based on the sensory measurements, the ACC-equipped vehicle can automatically regulate its speed to maintain a suitable spacing with the detected predecessor.In the absence of any preceding vehicle, the ACC system functions like a conventional cruise control (or speed control) system that takes over the throttle of the vehicle to maintain a target speed as set by the driver.However, for an ACC-enabled vehicle platoon, a limitation is that the resulting gaps between consecutive vehicles are often relatively large, which is undesirable for traffic efficiency and may also lead to unnecessary“cut-in” and “cut-through” operations of non-platoon vehicles.As an extension of ACC, cooperative adaptive cruise control(CACC) [2], [3] has yet been investigated extensively for automated vehicles.What distinguishes CACC from ACC is that it empowers vehicle-to-vehicle (V2V) communications to achieve longitudinal vehicle control.Specifically, CACCequipped vehicles employ not only the relative positions and velocities measured from vehicles ahead through on-board ranging sensory technology but also the received data (e.g.,position, velocity, acceleration) from surrounding vehicles via pervasive wireless communications.A notable advantage of a CACC-enabled platoon is that shorter vehicle-following distances are made possible, thereby enabling better road capacity and especially greater fuel efficiency in the case of heavyduty vehicle platoons [4], [5].

The introduction of wireless V2V communications to vehicular platoons greatly facilitates versatile information sharing among automated vehicles beyond line-of-sight of onboard sensors.However, wireless communications ineluctably induce several challenging issues worthy of careful consideration during stability analysis and control design of CACCenabled platoons.For example, due to the digital nature of wireless communications, the vehicular data to be shared over wireless V2V communication channels should first be sampled and then be encapsulated into packets before possible network transmissions.More concretely, the desired vehicle platooning controllers and algorithms allow to use only packet-based vehicular data and to be updated at merely discrete instants in time.This makes the existing platooning con-trol methods based on continuous-time vehicular data (e.g.,[6]-[14]) inapplicable or even invalid in a digital wireless communication setting.

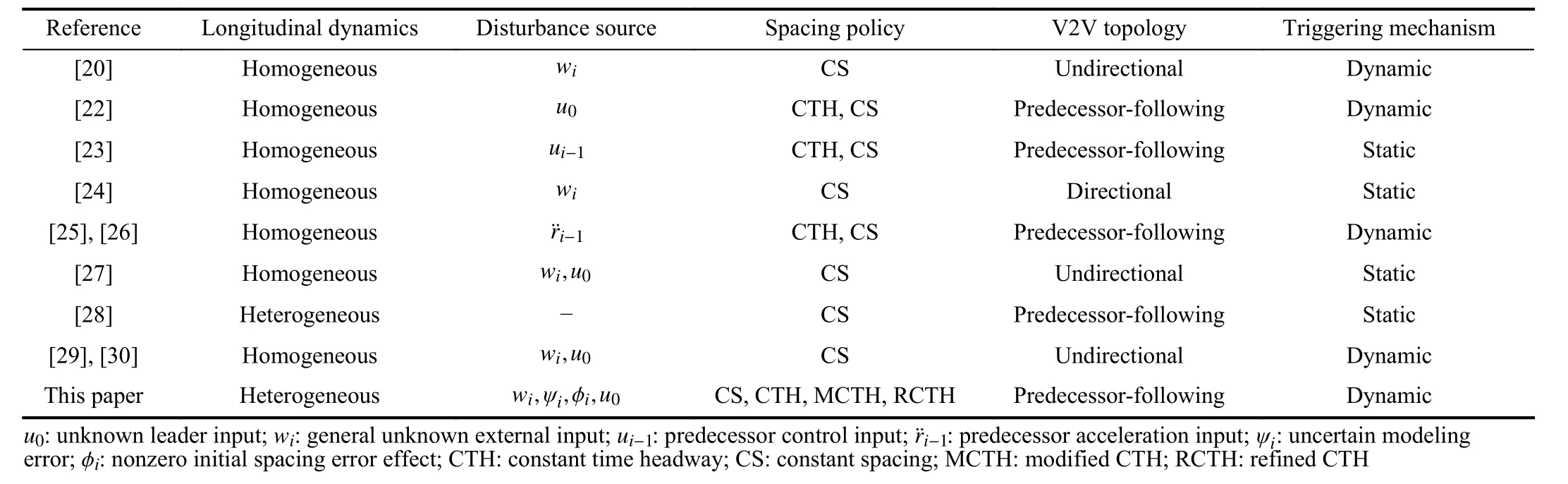
TABLE I COMPARISON BETWEEN THIS STUDY AND SOME EXISTING EVENT-TRIGGERED PLATOONING CONTROL LITERATURE

A wireless communication network may also suffer from restricted data rates due to its finite bandwidth.For example,the PHY payer of dedicated short range communications(DSRC) under an IEEE 802.11p/WAVE standard offers constrained data rates from 3Mbps to 27Mbps in 10MHz channels [15].From the perspective of resource efficiency, the existing continuous-time or time-triggered platooning control methods [6]-[14], [16], [17] inevitably lead to over-utilization of available sensor (or transmitter) energy and bandwidth resources.This is because they demand the vehicular data to be continually perceived by sensors and to be persistently transmitted over the wireless channels.Furthermore, in many practical scenarios, platoon vehicles are more likely to instantaneously share their data with both platoon and non-platoon vehicles in proximity as well as other road infrastructures across multiple lanes.This unavoidably produces a huge amount of vehicular and traffic data whose acquisitions and transmissions may put an extra burden on the limited sampling and communication resources.It is thus of great significance to develop a communication resource-efficient scheduling mechanism such that the V2V data transmissions among CACC-equipped vehicles occur only in an intermittent and sporadic manner, leading to an economic use of the scarce resources.

Event-triggered control is regarded as a promising alternative to the traditional continuous-time and periodic sampleddata control approaches for a wide variety of networked control systems since it can achieve a trade-off between desired control performance and satisfactory communication efficiency.Specifically, when an event-triggered mechanism is employed to schedule vehicular data transmissions over wireless V2V channels, it means that the vehicular data on each sensor is not transmitted unless it is “required” (e.g., when the vehicular data experiences a significant change).Therefore,the continual occupancy of the constrained energy and bandwidth resources can be notably alleviated.Despite fruitful results on event-triggered control for general networked control systems [18], [19] and multi-agent systems [20], [21],there have been a few results available on event-triggered platooning control, such as [22]-[30].The main differences between those studies and this paper are clarified in Table I in terms of the considered longitudinal dynamics, disturbance sources, spacing policies, V2V topologies, and triggering mechanisms, respectively.

One of the key challenges in event-triggered platooning control originates from the design of an intrinsically Zeno-free event-triggered platoon controller to guarantee practical implementation of the event-based transmitter and controller,while also preserving desired platoon control performance in the presence of various disturbances.Furthermore, it is noteworthy that the dynamic event-triggered platooning control in[22] corresponds to an emulation problem, meaning that a CACC law is first designed in continuous-time, ignoring any network constraints and implementation details, and an eventtriggered mechanism is then proposed to meet as closely as possible the control performance of the continuous-time design.Since the controller is intrinsically designed for addressing a network-free control problem, the resulting control performance may not necessarily be close to that in a networked control design problem.Meanwhile, the dynamic event-triggered platooning controllers in [25], [26] rely on the given or preselected feedback gains without adhering an inherent co-design procedure.Therefore, another challenging issue is to develop a co-design approach that elaborates a truly joint design of distributed CACC controllers and dynamic event-triggered mechanisms.

The desired platoon control objective generally consists of two aspects: individual vehicle stability and string stability.The former is to guarantee small, but not necessarily constant,longitudinal distances between successive vehicles and achieve harmonious speed/acceleration of the platoon.The latter can be deemed as a requirement for platoon safety and traffic efficiency that the resulting spacing errors or speed profiles do not get amplified against any disturbance as they propagate from one vehicle to another.The definition of string stability in the literature is rather diverse [10], [12], [31],among which the L2-string stability [8], [22], [23], [32] is prevalently adopted.More specifically, the L2-string stability guarantees the accumulated energy of the spacing error does not become enlarged from one vehicle to another.However, a platoon control system achieves one form of string stability but may remain unstable in another sense [31].Furthermore,multiple experimental studies show that the controlled platoon vehicles that comply with some string stability measures may still exhibit an overshoot during transient stages, causing collisions in long platoons [33].In practice, it is more preferable that the spacing error of each vehicle does not exceed some safety boundat any timein such a way as to guarantee absolute collision avoidance.Such platoon safety becomes more pressing in the context of event-triggered platooning control because much fewer real-time vehicular data packets are transmitted and used to execute CACC laws.

Motivated by the above observations, in this paper, we investigate the resource-efficient platooning control problem for a convoy of CACC-enabled vehicles under sporadic V2V communications, different spacing policies, and various disturbances.The novelty of the paper lies in the development of a dynamic event-triggered scheduling and platoon control codesign approach for the problem above, under which desired platoon stability and performance as well as satisfactory communication efficiency can be guaranteed simultaneously.

The specific contributions of the paper are summarized as follows.1)A dynamic event-triggered communication scheduling mechanismis developed to reduce the frequency of V2V communications between adjacent vehicles.It is shown that such a scheduling mechanism offers more flexibility and efficacy than some existing ones;2)A refined constant time headway spacing policyis proposed to integrate the salient features of the existing constant spacing and constant time headway spacing policies, and also to incorporate the nonzero initial spacing conditions; and3)A tractable co-design criterionis derived to determine the feasible gain/matrix parameters for both the desired event-driven CACC controllers and the proposed scheduling mechanism.

Notations: R≥0(correspondingly, N≥0) denotes the set of non-negative real numbers (correspondingly, non-negative integers).If a matrix is invertible, the superscript “ -1” represents the matrix inverse.I (correspondingly, 0) represents the identity matrix (correspondingly, zero vector or matrix) of an appropriate size.‖·‖ denotes the Euclidean norm of a vector.⊗denotes the Kronecker product.The superscript “T” stands for the transpose of a matrix or vector.Matrices, if not explicitly stated, are assumed to be dimension-compatible.Other notations used throughout the paper are quite standard.

The rest of the paper is organized as follows.Section II presents the vehicle longitudinal model, the spacing policies,and the event-based CACC law, and further formulates the main problem to be addressed.Section III elaborates the dynamic event-triggered communication scheduling mechanism.Section IV provides a sufficient condition for the platoon stability and performance analysis.Section V states the co-design criterion on the existence of event-driven CACC controllers and triggering mechanisms.Section VI shows extensive numerical case studies on a seven-vehicle platoon.Section VII concludes this paper with potential extensions.

II.PROBLEM FORMULATION

A. Heterogeneous Vehicle Longitudinal Dynamics

Consider a convoy ofN+1 automated vehicles using a cooperative longitudinal control strategy for the vehicle-following objective.The vehicle, indexed by 0, is denoted as the leader and theother vehicles,indexedbyi∈V={..1.,2,...,N},areassignedasthe followers.Letri(t),r˙i(t),r¨i(t),ri(t)be the longitudinal position, velocity, acceleration, and jerk of vehicleiat timet∈R≥0, respectively.The following third-order differential equation is employed to model the heterogeneous longitudinal dynamics of each vehicle:

where τidenotes the lumped actuation lag in seconds associated with the engine, actuators, and drive-line of vehiclei,which is unknown to system designers;ui(t) is the commanded control input to vehiclei; andwi(t) denotes the generally unknown disturbance input.

To tackle the heterogenous and unknown lag τi, we let τi=τ0+τ˜i, where τ0and τ˜irepresent the nominal part and the uncertain part, respectively.Then, the heterogeneous longitudinal dynamics (1) can be described as

B. A Refined Constant Time Headway Spacing Policy

The real-time longitudinal spacing between vehicleiand its predecessori-1 is expressed asdi(t)=ri-1(t)-ri(t)-li-1,i∈V, which is calculated from the front bumper of the following vehicleito the rear bumper of the preceding vehiclei-1, as shown in Fig.1, whereli-1denotes the length of vehiclei-1.Then, the spacing error between vehicleiand its predecessori-1 is given by

wheredir(t) represents the desired longitudinal spacing between any two adjacent vehiclesiandi-1, ∀i∈V, at timet∈R≥0, which will be specified later.

For anyi∈V, the relative velocity and acceleration between vehicleiand vehiclei-1 can be described by

The platooning control begins with the design of a suitable spacing policy that specifies the desired longitudinal vehicle followingdistancedir(t).In the literature,thefollowing two spacingpolicieshavebeen extensively studied.

1)A speed-dependent spacingpolicy, where the desired longitudinal gap is a non-decreasing function of the velocity of a vehicle.Typically, theconstant time headway(CTH) policy of the following form [8], [14], [22], [23], [26] receives considerable attention:

whered0denotes the safe margin andhddenotes the time headway for vehicleiarriving at its predecessor’s position.

2)A constant spacing(CS) policy [6], [7], [11], [13], [16],[17], [20], [24], [29], [30],

whereD0denotes the prescribed constant inter-vehicle distance that may be made as small as the safe margin.The CS policy can be regarded a special case of CTH by lettinghd≡0 andD0≡d0.

A significant issue in the spacing policy design is to deal with the nonzero initial spacing errors, which can generally lead to overshoot in positions and thus potential collisions[34].In other words, some existing string-stable platooning control methods under the assumption of zero initial spacing errors may become string-unstable when the actual initial errors are not zero [35].Hence, great attention has been paid to platooning control under nonzero initial conditions/errors[34]-[36].In this study, one of our aims is also to rule out such an assumption of zero initial conditions/errors.For this purpose, we propose the followingrefined constant time headway(RCTH) spacing policy:

where the relative velocity is adopted, which can be obtained via either an on-board sensor or a V2V communication link.Then, the spacing errorin (3) can be represented by

The RCTH (7) inherits both the prominent features of the above CTH and CS policies.For example, when the preceding vehiclei-1 performs a sudden braking or the ego vehicleisuffers from a disturbance, causing a large transient engine torque and further a higher speed than its predecessori-1, the desired spacingdir(t) will increase accordingly to prevent potential collision.However, when the predecessori-1 is speeding up, a relative smalldir(t) ( ＜d0) will be set to accelerate vehicleiso as to catch up with its predecessor.On the otherhand,duringsteadydriving,the desired spacingdir(t)in(7)willbe closetothesafedistanced0with an aimtoimprove the road capacity.In the literature, a similar relative speed dependent spacing policy is studied in [35], [37], which is referred to as a modified CTH (MCTH) and can be expressed as

One can see that instead of using the predecessori-1’s velocity, the platoon leader’s velocity informationr˙0(t) is adopted.This, however, indicates that, in order to implement the designed platoon control law, all platoon members are required to obtain the accurate and continuous leader’s velocity informationr˙0(t), which inevitably poses additional connectivity configuration and implementation costs to practical platooning.Given the limited communication resources, this is also burdensome when the scale of the platoon becomes large.In a nutshell, the RCTH above is capable to warrant higher traffic efficiency than the traditional CTH during steady driving and improved safety requirement over the conventional CS during non-steady driving, and can be implemented by all platoon members in an autonomous manner without persistent leader information.Hereinafter, the time dependency “(t)” of the continuous-time signals may sometimes be left out for conciseness whenever without causing any confusion.

C. An Event-Driven CACC Law

For each platoon vehiclei∈V, the traditional continuous CACC law can be constructed as

which essentially consists of two parts: i) awireless communication-based control term, which necessitates the velocityr˙i-1and accelerationr¨i-1from its predecessori-1.This can be received via establishing a DSRC link under the IEEE 802.11p standard; and ii) anon-board measurement-based controlterm,whichrequirestheactualspacingdiand alsothereal-timevelocityr˙iandaccelerationr¨iofvehiclei.The actual spacing can be measured via a radar or lidar unit

More specifically, instead of constructing a continuous CACC law (10) for each vehiclei∈V, we are interested in the design of an event-driven CACC law of the following form:

D. The Problem to Be Addressed

The string stability analysis aims to attenuate uniformly the effects of the disturbances along the string [8], [22], [23], [32].This is a challenging task here because of the concerned heterogeneous platoon, multiple disturbance sources, various spacing policies, and particularly the intermittent event-based CACC law.In what follows, we choose theH∞norm of the errors as a performance measure to attenuate the effects of bounded disturbances.Thus, denote byzi=Ceithe desired performance output to be evaluated withCbeing a given matrix andbeing the augmented error vector.Further define the following stacked vectors:

The main problem to be addressed is stated as follows.

III.A DYNAMIC EVENT-TRIGGERED COMMUNICATION SCHEDULING MECHANISM

Fig.2.The schematic of an event-driven control structure on the CACC-equipped automated vehicle indexed by i.

where

Remark 3: From the perspective of triggering principle, (17)is distinct from the one studied in [22] where the threshold (or tuning) parameters are fixed but additional auxiliary dynamic variables are inserted in the triggering conditions to reduce data transmissionsas much as possible.Since there is an inherent trade-off between real-time control performance and communication efficiency within the context of event-triggered control, it is imaginable that the dynamic triggering mechanism in [22] inevitably trades more real-time control performance than its static counterpart in exchange for significant resource utilization reduction.The triggering mechanism in [30] employs some adaptive threshold parameters that can dynamically adjust their values over time.However, a potential limitation is that both the adaptive triggering mechanism and control law have to be co-located with the agent/plant due to the common adaptive parameter.It is also noteworthy that(17) intrinsically excludes the Zeno behavior due to the periodic sampling nature of all signals involved.Nevertheless, the triggering conditions in [22], [30] rely on the continuous-time signals and thus demand continual event detection at any timet∈R≥0.On the other hand, an adaptive design procedure is provided in [25] to select appropriate thresholds for accommodating different communication failure probabilities, while the triggering mechanism essentially constitutes a fixed threshold parameter and the desired controller parameters are chosen without considering the adaptive nature of the threshold parameter.The dynamic triggering mechanisms proposed in[26], [29] exhibit a similar triggering principle as the proposed one in (17).However, the threshold parameters in [26],[29] are adjusted in amonotonicmanner.For example, the one in [26] includes a monotonically decreasing dynamic threshold parameter, which implies thatmoredata packets are generally released over the communication channel than the traditional static triggering mechanism in order to seek better realtime control performance.

IV.PLATOON STABILITY AND PERFORMANCE ANALYSIS

In light of the errors (4) and (8) and the RCTH (7), the resulting longitudinal tracking error dynamics of thei-th platoon vehicle can be derived as

Note that the event releasing interval can be rewritten by a union of a series of subintervals

Then, a piecewise continuous delay functionh(t)=t-mTsis introduced on each subinterval, which satisfies that

where C =[(I⊗C),0,0,0,0,0]Tand

Proof: See Appendix.■

V.COMMUNICATION AND CONTROL CO-DESIGN

However, in practice, the above disturbances and the initial condition are often unknown prior to the design process.Hence, without loss of generality, one may regard α in Theorem 2 as a tuning parameter that enables a trade-off analysis between theH∞performance and the other performance requirements.

VI.NUMERICAL SIMULATIONS

for the platoon over the time interval [0,80) s, whereRirepresents the individual transmission rate on vehicleiwithdenoting the number of events and N being the number of total sampled data packets.Furthermore, we define

as theaverage spacing errorand

as themaximal average absolute spacing error, and use both as platoon performance metrics for quantitative comparison.

A. Event-Driven Platooning Control Under RCTH and Nonzero Initial Conditions

Fig.3.Event triggering instants { tkiTs} and triggering intervals { (tik+1-tki)Ts}, i ∈V, generated by (17).

In this case study, we evaluate the communication scheduling and platoon performance under the proposed event-driven RCTH-based CACC law.The individual spacing error bound is set as=1 m, which implies that=6 m.The nonzero initial states of the platoon members are randomly chosen.

Applying Theorem 2 (with ρ =0.13, α =200 , and γ =10), it is found that the concerned platooning control problem is feasible with=23.14% and=0.5185 m.The triggering instants and releasing intervals generated by the proposed scheduling mechanism (17) are demonstrated in Fig.3.It is clearly seen that the resulting inter-event times are significantly larger than the sampling periodTs.A large number of sampled vehicular data packets, i.e., averagely 76.86% of the total sampled packets, can be prevented from broadcasting over the wireless V2V communication channels, which confirms the significantly improved communication efficiency under the proposed event-driven platooning controllers.

The relative positions, the velocities and accelerations, the actual spacings, and the resulting spacing errors of each platoon vehicle are plotted in Fig.4, respectively.It can be observed that the imposed external disturbanceswi(t) on each follower vehicle and the leader control changesu0(t) both have certain adverse influences on the desired platoon performance.More specifically, the external disturbanceswi(t)result in oscillating fluctuations of the vehicular accelerations and velocities during [55,65] s due to their large amplitudes,and the leader control variations cause some spikes on the following vehicles’ accelerations and velocities.However, their impacts on the platoon behavior are effectively attenuated by the proposed event-driven CACC controller in (14).It is noteworthy from Figs.4(d) and 4(e) that remarkably decreasing amplitudes of the actual spacings and the resulting spacing errors are ensured from the first vehicle to the tail vehicle,which demonstrates a string-stable platoon behavior under the proposed co-design approach.

Furthermore, from Figs.4(e) and 4(f), one can see that both the individual spacing errors(t) and the overall spacing errorsed(t) are regulated well below the specified error bounds at any timet∈R≥0, which thus guarantees the prescribed platoon spacing performance and meets the practical driving safety requirement.

For comparison purposes, we next apply Theorem 2 to test the above platooning scenario when the prescribed platoon spacing performance (16) isnottaken into account.This can be done by removing the second inequality constraint in (23).It is found that the problem is feasible under a lower average datatransmissionrate of=13.88% buta largermaximal averageabsolutespacingerror ofs=1.0351m.Thecorresponding relative positions, velocities, accelerations, spacings,and spacing errors of the platoon vehicles are depicted in Fig.5,respectively.Clearly, without the prescribed platoon spacing guarantee, the platoon vehicles maintain relatively larger spacings between each other in the presence of the leader control command variations and external disturbances.More specifically, Fig.5(a) shows that the actual spacing between the platoon member 1 and the platoon leader at timet=39.1 s is about 1.8296 m, which may be not safe enough for practicalplatooning.In contrast, the actual spacing between the platoon member 1 and the platoon leader at timet=39.1 s becomes 3.2014 m when the prescribed platoon spacing performance (16) is considered, which offers improved safety against potential collisions.The superiority of embedding the prescribed spacing requirement in the event-driven CACC controllers can be also noted from comparing the overall platoon behaviors in Fig.4 with those in Fig.5.

Fig.4.Time responses of the closed-loop platoon control system under RCTH and nonzero initial conditions with the prescribed spacing performance:(a) Relative position to the leader r0(t)-ri(t); (b) Velocity r˙i(t); (c) Acceleration r¨i(t); (d) Spacing di(t); (e) Individual spacing error edi(t)=di(t)-dir(t) and bound δi=1, i ∈V ; (f) Stacked spacing error ‖ ed(t)‖2 and bound Δ=6.

Fig.5.Time responses of the closed-loop platoon control system under RCTH and nonzero initial conditions without the prescribed spacing performance:(a) Spacing d i(t); (b) Individual spacing error e di(t) and bound δi=1, i ∈V ; (c) Stacked spacing error ‖ ed(t)‖2 and bound Δ=6.

We further present comparative results ofand(t)as well asin different cases of the specified spacing error bound δiand sampling periodTs, which are summarized in Fig.6.It can be observed that i) Smaller specified spacing error bounds δiare generally pursued at the expense of communication efficiency, as shown in Figs.6(a) and 6(b).This reasonably demonstrates that more sampled vehicular data packets are required to be transmitted over the wireless communication network in such a way as to achieve better platoon performance; and ii) Under the specified spacing bound δi=3.5 m, larger sampling periodsTsresult in higher average data transmission rates over the network due to the generally prolonged sampling and transmission intervals.Furthermore, Figs.6(c) and 6(d) indicate that the resultant platoon performance becomes degraded to a certain extent when a large sampling period is configured, given fewer real-time vehicular data can be sampled and released over the V2V network for control implementation.

B. Event-Driven Platooning Control Under Different Spacing Policies

In this case study, we verify the proposed communication scheduling and control co-design approach via examining different spacing policies under zero initial conditions.

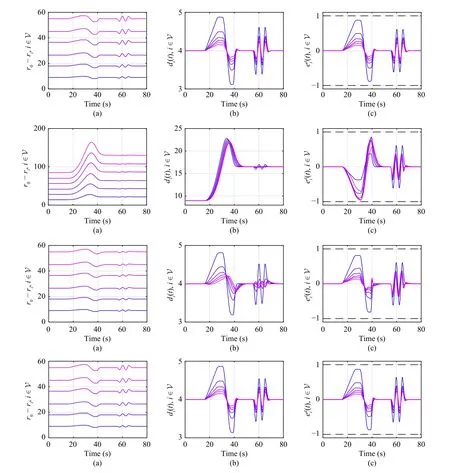
Fig.8.Comparison of the relative position to the leader, spacing, and spacing error of all vehicles in the platoon under CS (the first row), CTH (the second row), MCTH (the third row), and RCTH (the last row) policies: (a) Relative position to the leader r0(t)-ri(t) ; (b) Spacing di(t); (c) Individual spacing error edi(t)and bound δi=1, i ∈V.

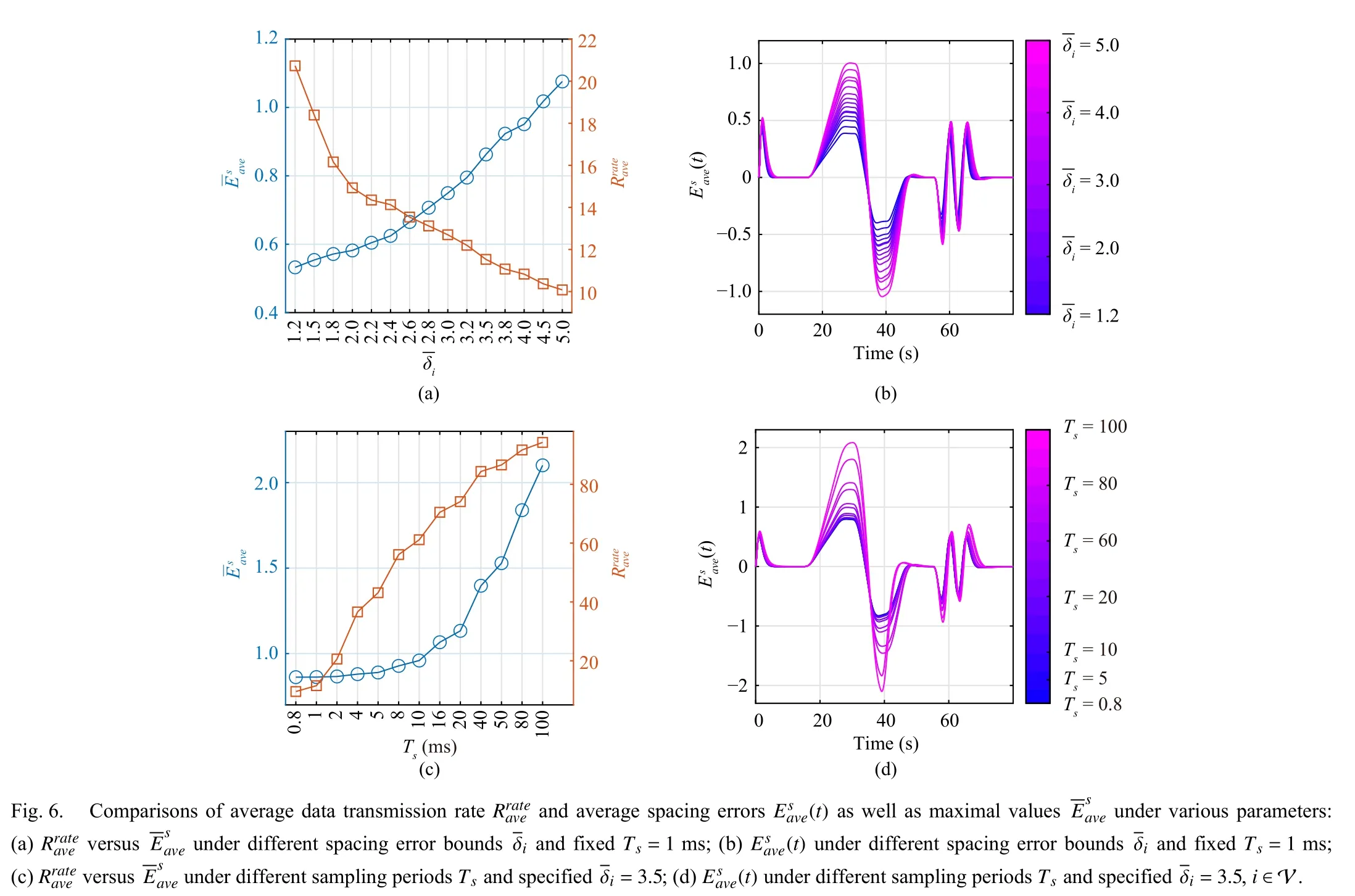
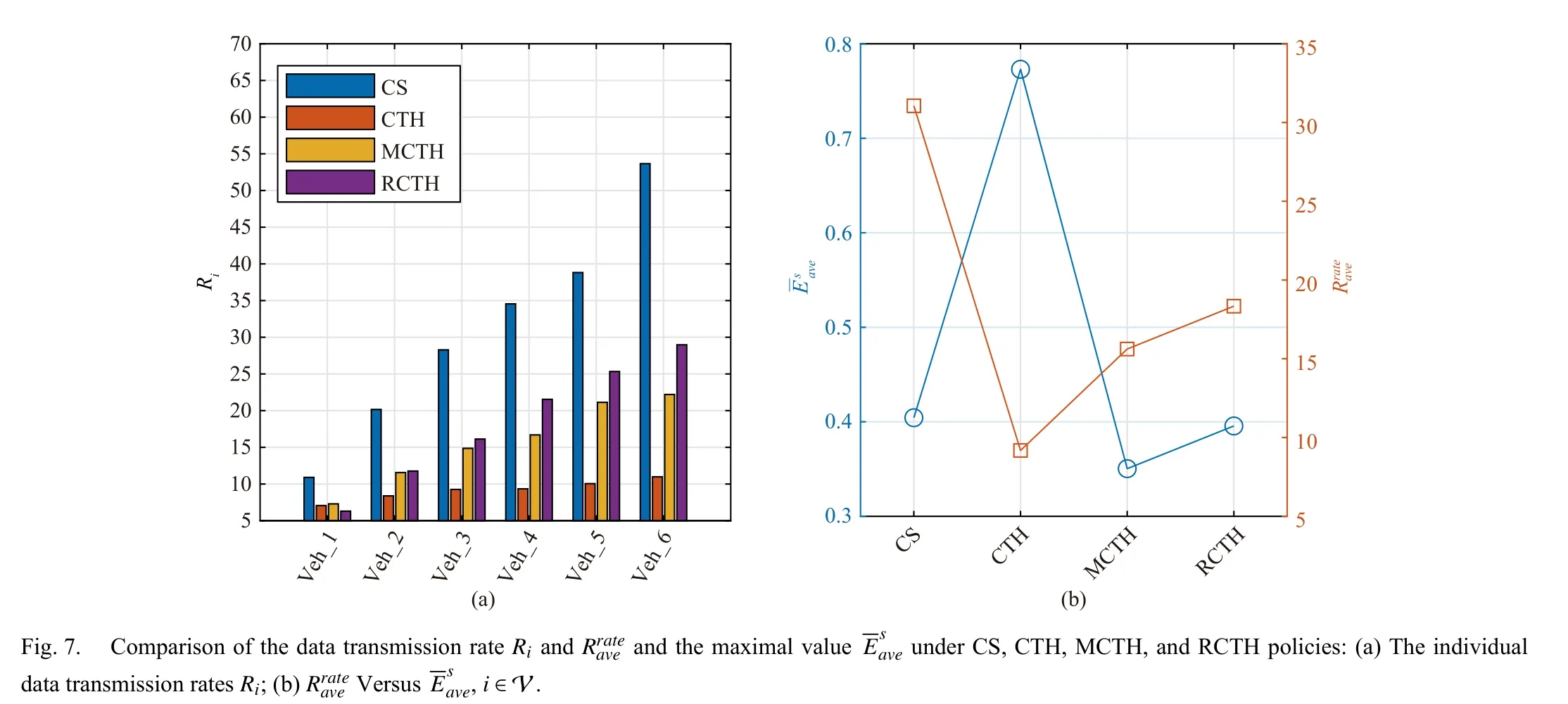
Applying Theorem 2, it is found that the concerned problem is solvable in all cases of CS, CTH, MCTH, and RCTH.The simulation results are provided in Figs.7 and 8.More specifically, Fig.7 illustrates the individual data transmission ratesRion each platoon vehicle, and the comparisons betweenandRunder different spacing policies.Fig.8 presents the resultant time responses of the relative positions to the leader, the actual inter-vehicle distances, and the spacing errors of the controlled platoon vehicles, respectively, under different spacing policies.

The following observations are noted from Figs.7 and 8:i) Overall, the proposed co-design approach demonstrates similar or close platoon control performance under the CS,MCTH, and RCTH policies, which can be seen from the approximately equalin Fig.7(b) and similar spacingsdi(t) and spacing errorsedi(t) in Figs.8(b) and 8(c).The reason behind this is that CS, MCTH and RCTH can both ensure the small safe marginduring steady driving stages; ii) The CTH-based platoon leads to the lowestthan the other spacing policies, while the resultingis the worst, as clearly depicted in Figs.7(b) and 8 (the second row).A possible reason is that the speed-dependent CTH policy leads to much smoother platoon behaviors even during transient stages, as shown in Fig.8(b) (the second row), while the triggering mechanism typically relies on signal variations.On the other hand, CTH can always ensure larger gaps between vehicles and thus frequent data transmissions may be not necessary for spacing regulation; and iii) Albeit MCTH shows both slightly better communication efficiency and platoon control performance than RCTH, as shown in Figs.7(b) and 8 (the second and third rows), the MCTH-based CACC law on each platoon follower persistently demands the leader’s velocity information, which implies extra communication overhead.However, allowing each platoon follower to be continuously informed by the leader offers a potential to improve the platooning control performance.

The relative position of the tail vehicle to the leader, i.e.,rN(t)-r0(t), represents the dynamic length of the platoon on the road, and thus is directly related to the traffic throughput.As can be seen from the first column of Fig.8, the controlled platoon under CS, MCTH, and RCTH performs remarkably well by guaranteeing steady gaps and smaller dynamic platoon lengths, thereby greatly improving traffic efficiency.Instead, the CTH spacing policy results in a relatively loose platoon over time and leads to considerably large gaps during high-speed driving.In other words, the CTH-based platooning control strategy sacrifices certain level of traffic throughput in exchange for driving safety.It is also noteworthy that large gaps in the platoon may leave the door open for humandriven vehicles to perform unnecessary “cut-in” and “cutthrough” operations, which is unfavourable for practical platooning.

Summarizing the simulation results presented above, it can be concluded that the proposed co-design approach enables a comprehensive trade-off analysis between the desired platoon performance (individual stability, disturbance attenuation performance, spacing/safety requirement, traffic throughput) and the satisfactory communication efficiency.

VII.CONCLUSIONS

The resource-efficient CACC design problem for automated vehicle platoons is addressed.A new co-design approach for communication scheduling and CACC design is developed to ensure the existence of the admissible eventdriven CACC law and the dynamic event-triggered scheduling mechanism.Furthermore, a co-design criterion is derived to guarantee both the desired vehicle-following control performance and platoon robustness against various disturbances as well as the prescribed spacing performance.Finally, numerical case studies are presented to demonstrate the effectiveness and advantages of the co-design approach.

This study is devoted to preserving the simultaneous communication efficiency and platoon control performance for CACC-enabled automated vehicles.As a potential future work, it would be interesting to develop novel communication-efficient platooning controllers that further guarantee satisfactory operational performance, such as fuel efficiency[38], energy saving [39], emission reduction [40].It would be also significant to embed suitable security mechanisms [41] in the proposed communication-efficient platooning control framework to counteract the adversarial effects of malicious cyber attacks on V2V communication channels.As another potential extension, the resilient communication-efficient platooning control design is highly desirable when various and concurrent network-induced constraints (e.g., communication delay and failure, data loss and disorder, finite bit rate, data quantization, channel fading) are present.

APPENDIX PROOF OF THEOREM 1

Choose the Lyapunov functional candidate asV(e(t))=V1(e(t))+V2(e(t)),t∈Ωm, where

with ϱ (q)=e(q)-e(mTs).AlthoughV(e(t)) is discontinuous at instants {mTs}, following a similar analysis in [29], it can be derived thatV(e(t))≥0andlimt→mTs V(e(t))≥V(e(t))|t=mTs.Theproofis dividedintothreeparts.

Part 1(Proof of the individual stability): From the closedloop system (21), the following zero equation:

holds for arbitrary matrix Θ and scalar ρ ＞0.

On the other hand, from the scheduling mechanism (17), it is clear that for anyt∈[tkiTs,tki+1Ts), the following inequality:

holds, which can be written as

with ε ˜=e(t-h(t))+ϖ(t-h(t)).

Calculating the time derivative ofV(e(t)) and combining the left-hand sides of (29) (under zero φ) and (31), it is easy to obtain that

which indicates theH∞performance index (15).

Part 3(Proof of the prescribed spacing performance): From(33), one gets that

Integrating its both sides from zero to anyt＞0, we obtain