均匀磁场下二维拓扑绝缘体边缘态的多重Andreev 反射研究

杨 雪，吕 博

（天津大学，天津 300350）

0 引言

拓扑绝缘体[1]存在无能隙的表面态，其表面态是自旋非简并的。典型例子是量子自旋霍尔绝缘体（QSHI）[2⁃4]，其是一个表现出量子自旋霍尔效应的二维系统。QSHI 的边缘态形成“螺旋态”，因为其沿着同一边缘、相反的自旋反向传播。在HgTe/CdTe[5]和InAs/GaSb[6]等量子阱结构的输运测量中，揭示了这些螺旋边缘态的特征，使QSHI 成为一个很有前途的研究拓扑超导体平台。传统的超导体连接到这种边缘态可以通过近邻效应[7]诱导出拓扑超导性，并且拓扑超导体在与拓扑平庸区域的界面处能产生马约拉纳束缚态（MBSs）。正如傅亮和C.Kane 提出在拓扑绝缘体表面态上耦合常规超导体可以实现拓扑超导[8]，在该系统中出现了MBSs。

MBSs 的一个显著特征是分数约瑟夫森效应[9]。在传统的约瑟夫森结中，超电流在电流⁃相位关系中是2π周期的[10]。实验方面，在HgTe/超导体杂化物中观察到缺失的奇数Shapiro 台阶。相比之下，两个超导体之间的MBSs 可以产生4π 周期的超电流和受到拓扑保护的4π 周期的Andreev 束缚态[11⁃12]。这种效应在平衡约瑟夫逊实验中很难观察到，因为弛豫机制普遍存在，2π 周期性通常会被恢复。两个拓扑超导体之间的电压偏置约瑟夫森结可以表现出异常的电流⁃电压特性，这正是MBSs 的表现。在传统的约瑟夫森结中，施加偏置电压，会在电压Vn=2Δ/(en)处产生一系列共振电导峰[13⁃14]，其中n为整数，Δ为超导能隙。这是由于多重Andreev反射（MAR）[15⁃17]引起的亚谐隙结构（SGS）[18⁃19]。对于拓扑超导体，由于马约拉纳束缚态的出现，在能隙中间为准粒子的输运提供了新的通道，因此共振电导峰出现在Vn=Δ/(en)处。

在这项工作中，研究了在QSHI 边缘处的约瑟夫森结中MAR 的输运性质，沿量子自旋霍尔边缘的S 波超导体/正常金属/S 波超导体结的示意图如图1 所示。

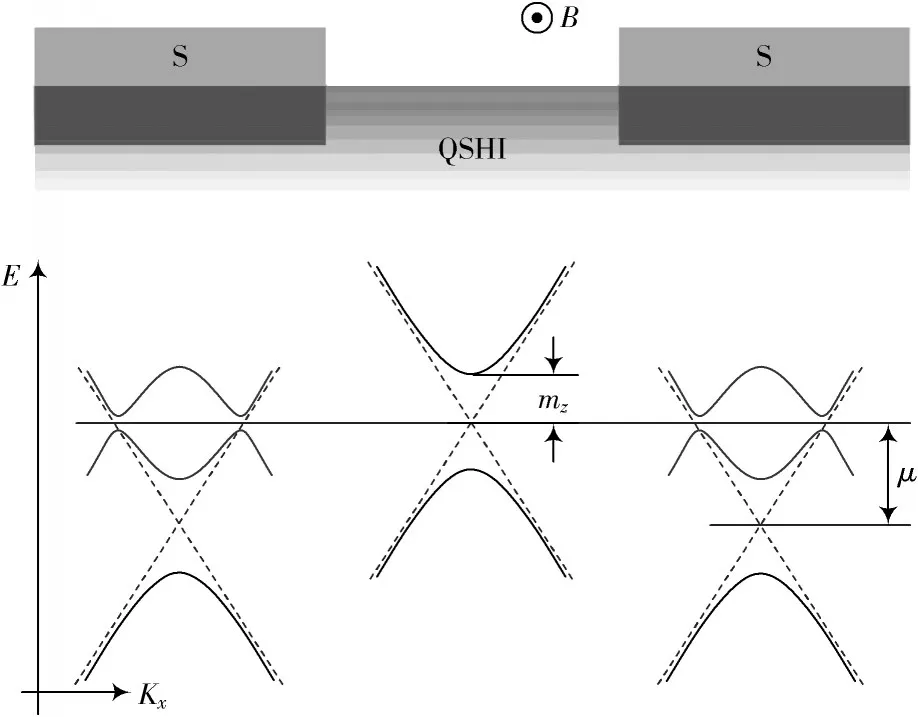
图1 S 波超导体/正常金属/S 波超导体结的示意图

图1 底部为每个区域的能谱，虚线表示无磁场的狄拉克型能带，μ是从狄拉克点测量到的化学势。在平面外磁场B中，能谱中一个2mz的磁隙打开。

在超导体一侧，考虑到近邻诱导的S 波超导能隙，通过接近铁磁绝缘体或施加平面外磁场可以得到与螺旋态的交换场耦合。前人对于MAR 的研究主要集中在分离的铁磁[20]和超导区域之间有畴壁，本文假设磁场强度延伸到整个系统，发现了不寻常的SGS，这与Badiane、Houzet 和Meyer[21]的工作相一致。值得注意的是，本文系统中的SGS 可以很容易地通过磁场强度调整。这一结果与拓扑螺旋态中超导和铁磁序之间的相互作用相对应。

1 模型与计算

为了清楚地表示QSHI 的边缘上的一个SNS 结，标记左侧超导体所在区域为S1，右侧超导体所在区域为S2。均匀磁场下，沿量子自旋霍尔边缘的超导体（S1）⁃正常金属（N）⁃超导体（S2）约瑟夫森结的示意图如图2 所示。图中坐标原点为超导体S1和N 的交界处，磁场沿z方向。

图2 约瑟夫森结的示意图

图2 中，约瑟夫森结中正常金属区N 区的宽度为L，假设其比超导相干长度ξ以及超导体中的弹性和非弹性散射长度要小得多。在基矢中，系统的BdG 哈密顿量为：

式中：U=μ(Θ(-x)+Θ(x-L))代表掺杂程度，μ为化学势；是自旋（Numbu）空间中的泡利矩阵；交换场M在磁场中是均匀的；对势Δ由Δ=Δ0(Θ(-x)+Θ(x-L))给出，假设Δ0≪Mz。设置ℏ=1，得到系统的BdG 方程为：

利用BdG 方程和BTK 理论，可求得超导体中电子型粒子的波函数和空穴型粒子的波函数分别为：

准经典近似下，Ze1≈Ze2，准粒子波函数Ψe1、Ψe2、Ψh1、Ψh2化简为：

因此，当电子型准粒子垂直入射时，在S1/N/S2结构中，S1区的波函数为：

在正常金属区，波函数为：

超导体S2区的波函数：

在势垒x=0 和x=L处利用波函数连续性条件，同时利用散射矩阵：

连接不同区域的准粒子波函数，可以得到：

得到散射系数An、Bn的递推关系：

根据电流守恒定律得到了平均电流：

式中：

本文只关注直流部分，即k=0 时的电流，它在实验中与长时间内的平均电流为：

2 结果分析

计算约瑟夫森结中的电流和电导，其随电压变化的趋势如图3所示。

图3 电流和电导随电压eV 变化的关系曲线

S/N/S 结在均匀磁场下，根据式（21），透明度D分别取0.3、0.5 和0.7，费米温度为0.2Δ，Δ=0.01，化学势μ=0.1，磁场强度Mz分别取Mz=0.2μ和Mz=0.5μ，得到了超导体结在均匀磁场下的电流、电导随电压eV之间的关系。

可以观察到SGS中，其特征是电流在电压为Δ/n（n为整数）时会发生明显跃变，在Δ/n处出现了零偏压电导峰，并且随着透射率D增大，电流跃变程度减弱。在电导图中可以很明显地看到这一现象：当D=0.3 时，位于同一电压处的电导峰是最尖锐的；随着D的增大，如D=0.5、D=0.7，电导峰逐渐平缓。

进一步，固定透明度D=0.5，通过调节磁场强度Mz与化学势μ的比值(r=Mz/μ)来改变磁场强度Mz，其他参数不变，研究电流与电压的关系，如图4 所示。图4 为S/N/S 结在均匀磁场下，固定透明度D=0.5，费米温度为0.2Δ，Δ=0.01，化学势μ=0.1，r分别为0.2、0.5 和0.8时的电流特性。为了更明显地看到不同情况下的电流特性，在图中进行了人为平移，正如图中的r=0.5 曲线和r=0.8曲线分别人为地增加了1个单位和2个单位。

图4 电流与电压的关系

结果表明，当透明度D不变，磁场强度Mz发生变化时，仍然出现亚谐隙结构，而且亚谐隙结构出现的位置随磁场的变化而变化，这说明亚谐隙结构受磁场的调控，为今后在磁场中研究隧道结提供了新的思路。

3 结语

本文研究了基于量子自旋霍尔绝缘体边缘的约瑟夫森结中的输运性质，分析了电流⁃电压关系。结果表明：在该系统中，S 波超导体/正常金属/S 波超导体结的隧道谱中存在亚谐隙结构，透明度只影响超导结的零偏压电导值的大小，并不会影响亚谐隙结构出现的位置。但是在磁场的作用下，亚谐隙结构发生了变化，不再固定地出现在Δ/n处，这是因为拓扑螺旋态中超导和铁磁序之间的相互作用，因此磁场是形成马约拉纳束缚态的必要条件。