基于遗传算法改进的AGV 路径规划研究

冯 舒，刘 明

（云南民族大学 电气信息工程学院，云南 昆明 650504）

0 引言

随着人们环保意识的增强，节能减排在路径规划中的应用被越来越多的研究者所关注，越来越多的学者开始关注物流体系中的碳排放问题[1]。寻找一条自动引导搬运车（Automated Guided Vehicle,AGV）绿色节能路径的研究课题受到极大重视。

目前，针对AGV 路径规划这一领域，已有很多学者进行研究。如：李健康等提出通过优化状态转移概率以及信息素更新的方法对蚁群算法进行改进，再应用于AGV 路径规划，获得更短路径[2]；熬国鑫等提出一种改进的BI⁃RRT 算法，引入可变权重实现目标导向，再对生成路径作剪枝优化，最后进行平滑处理，得到更加平滑且较短的路径[3]。

随着各行各业对于节能减排的需求越来越迫切，学者们开始考虑AGV 路径规划的能耗问题，并且AGV 能耗指标已得到工业界以及学术界的重视。为了实现节能减排与AGV 物流运输协同进行，一些学者开展了相关的探索和研究。例如：郭亚铭等对结合AGV 的转向和直行两种模式下的运动进行分析，建立单AGV 节能模型，利用Dijkstra 算法实现路径规划，得到距离短、能耗低的路径；李俊兰等提出一种结合改进Dijkstra 算法和非支配排序遗传法建立的AGV 节能模型来规划路径。但这些方法都存在一定程度的复杂性，并且很少考虑转角数目以及拐弯角度的大小，而这些因素对于AGV 的运动能耗影响很大[4]。

本文提出一种改进的遗传算法。首先对地图中的障碍物进行规则化处理，忽略不必要的冗余角点，降低计算复杂度以提高算法效率；其次，以路径长度为优化目标，且对遗传算法中的变异算子进行改进，使得路径总向对目标有利的方向进行变异，寻找到一条最短、转弯节点最少的路径。

1 相关算法

遗传算法是一种模拟生物遗传进化规律的原理来进行寻优的算法。它融合了“适者生存”“物竞天择”的择优方式以及遗传基因交叉变异的特点，将需要求解的问题通过编码形成染色体，模拟生物进化的过程，再通过种群迭代和选择、交叉、变异等步骤，并多次迭代和循环，筛选出最优秀的染色体，最优染色体对应的解就是该问题的最优解[5]。标准遗传算法流程如图1 所示。

2 算法描述

基于遗传算法对AGV 路径规划进行改进。首先本文对地图中的障碍物进行简化处理，改善角点过多的问题；再通过改进的遗传算法进行路径规划，得到最优路径。

2.1 障碍物规则化处理

该文将障碍物分为三类，分别为1×n（n∈R）的矩形障碍物、b×m（b，m∈R）的矩形障碍物以及不规则多边形障碍物。对于1×n的矩形障碍物，因宽度只为一个栅格，因此只在其尺寸为1 的栅格两侧旁各取一个角点即可，如图2 所示，浅灰色部分为角点栅格。针对b×m的矩形障碍物，以其4 个凸角点为栅格角点，如图3 所示。对于不规则多边形障碍物，将其填补为多边形的最小外接矩形，如图4 所示，灰色部分为填充部分，浅灰色部分为角点栅格。对障碍物简化后，在一定程度上减少了冗余节点，可为后续路径搜索做准备，有效提高搜索效率。

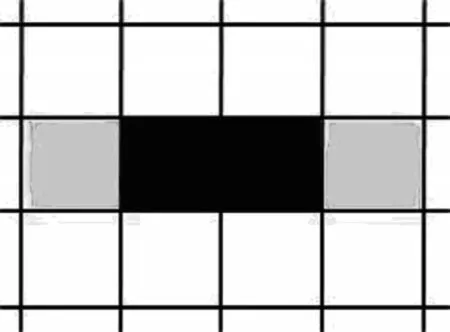
图2 1×n 矩形障碍物取点

图3 b×m 矩形障碍物取点

图4 不规则障碍物取点

2.2 算法描述及其实现过程

首先，根据连通性矩阵可知角点ai与哪几个角点连通，设从起始点ai到终点an之间，与ai连通的点有aj、ak、al、am，按角点顺序连通，比如aj的顺序排第一，则形成路径a1→aj。

若a1与终点an有直接连通性，则跳过所有中间连通角点直接与终点连接。若在连通过程中出现与之前已连通过的角点重复的角点，为避免路径出现死循环，则将两角点之间的连通性断开。

在连通过程中，如果某角点的所有连通角点在之前全部重复，则将连通关系全部取消，该角点无法到达终点。为了区别到达终点与未到达终点的路径，设置惩罚函数将两者区分，公式如下：

式中：Dall表示总路程长度；Df为已走完的路径；Ddnf为未走的路径；W为惩罚权重。本文将惩罚权重W设为5，将到达终点与未到达终点的路径明显区分开。

改进遗传算法的过程如下：

1）对角点种群进行初始化处理，种群数目大小为popsize，个体的基因长度为poplength，并对初始种群采用轮盘赌的方式进行选择，确定每个个体被选择的次数。

2）进行交叉操作，本文采用前一个种群个体与后一个种群个体进行交叉。

3）对种群个体进行变异操作，产生随机数rand，当随机数rand 小于变异概率Pm时，随机确定变异位置并对基因进行变异。

4）计算每个个体适应度值并按大小排序。

5）判断是否达到迭代次数最大值，达到则输出排名前10 的个体；如果不满足则返回步骤1）继续进行。

对于交叉变异，本文采用改进策略。首先，要找到合适的变异概率，一般会取一个很小的值。但是变异概率不宜很小也不宜过大，因为过大会破坏种群中的优良个体，过小则会使得种群过早收敛，这是由于在变异的过程中既会产生优良个体也会产生劣质个体[6]。本文针对这一问题对变异算子进行改进，过程如下：

1）设路径为：

2）若变异点的位置与其前后基因位置满足以下关系：当Nn+1-Nn-1=10 且Nn+1-Nn-1=1 时，则Nn-1、Nn、Nn+1形成45°角，此时，把基因Nn删除，形成新的路径。

3）若变异点的位置与其前后基因位置满足以下关系：当Nn+1-Nn-1=11 时，Nn-1、Nn、Nn+1形成90°角，则把基因Nn删除，形成新路径。

4）如果变异点基因的位置与其前后基因位置满足以下关系：当Nn+1-Nn-1=12，Nn+1-Nn-1=21 时，Nn-1、Nn、Nn+1形成135°角，就把基因Nn删除。此时新形成的路径为：

新形成的路径相较于改进前长度更短，拐弯数量更少，因此，变异概率选较大一些。本文取变异概率Pm=0.3。

3 实验仿真及分析

为检验改进算法的可靠性，将改进算法与遗传算法从搜索时间、路径长度、拐弯节点数、穿墙次数以及寻到的角点数等方面进行分析对比。本文的仿真在Matlab上进行验证。

首先对栅格图中的障碍物进行分类处理，用多边形障碍物变换为最小外接矩形等一系列方法来减少搜索角点数，再对各角点之间的连通关系进行判断；其次，为减少穿墙次数，改进算法将坐标数值改为栅格中心点的位置。这种方法相较于原先的常规数值坐标以栅格交点为中心点来说安全性更高，可以有效减少穿墙次数。坐标位置图如图5所示。图6为实际角点中心点连接图。

图5 坐标位置图

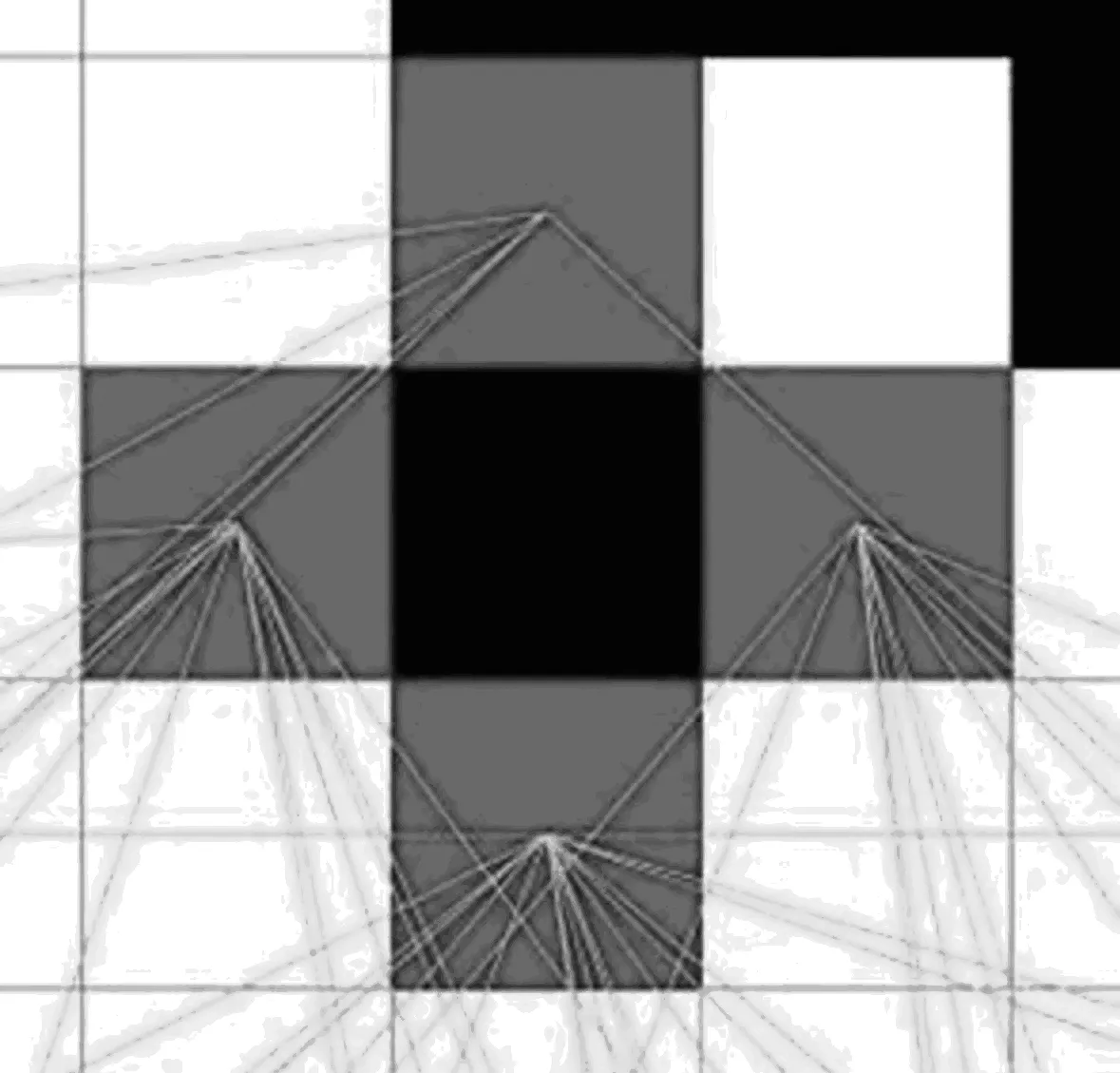
图6 角点中心点连接图

实验在100×100 的栅格中进行，图7 为改进后寻到的角点图，明显可以看出，改进后的角点相较于改进前角点数减少了很多，这为后续阶段的计算提高了效率，减少了计算量。图8 为所有角点的连通路径。

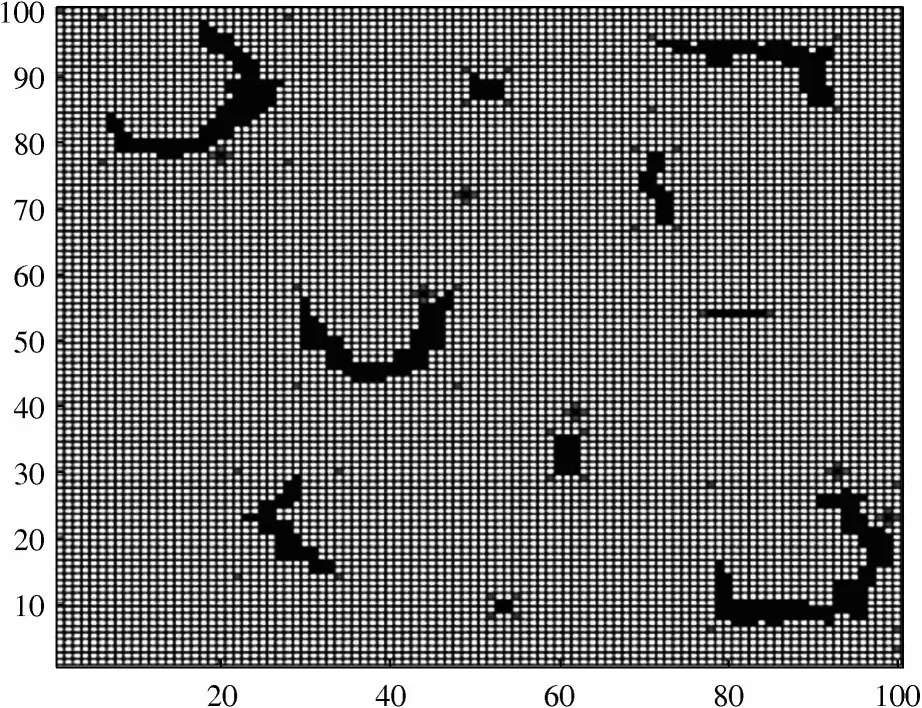
图7 改进角点图

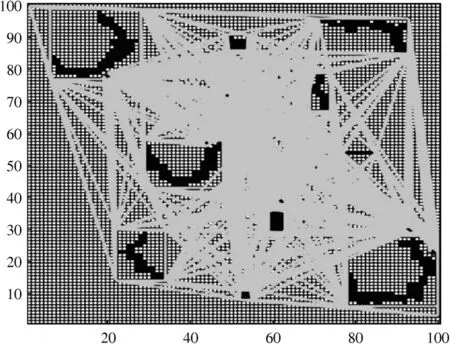
图8 角点连接图

图9 为遗传算法与改进算法在同一地图中的路径图，具体实验数据如表1 所示。由实验数据分析可看出：改进算法寻到的角点数目相较于普通遗传算法来说减少了68.8%，所用时间也略小于普通遗传算法；并且改进算法在速度方面能够更快地得到最佳路径，找到的路径长度也比普通遗传算法更短。改进算法全程无穿墙事件发生，安全性更高，且拐弯角点也更少，有益于降低能耗。

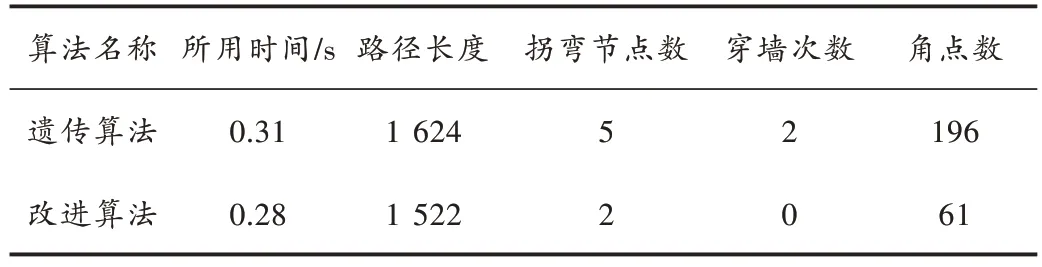
表1 两种算法实验数据对比

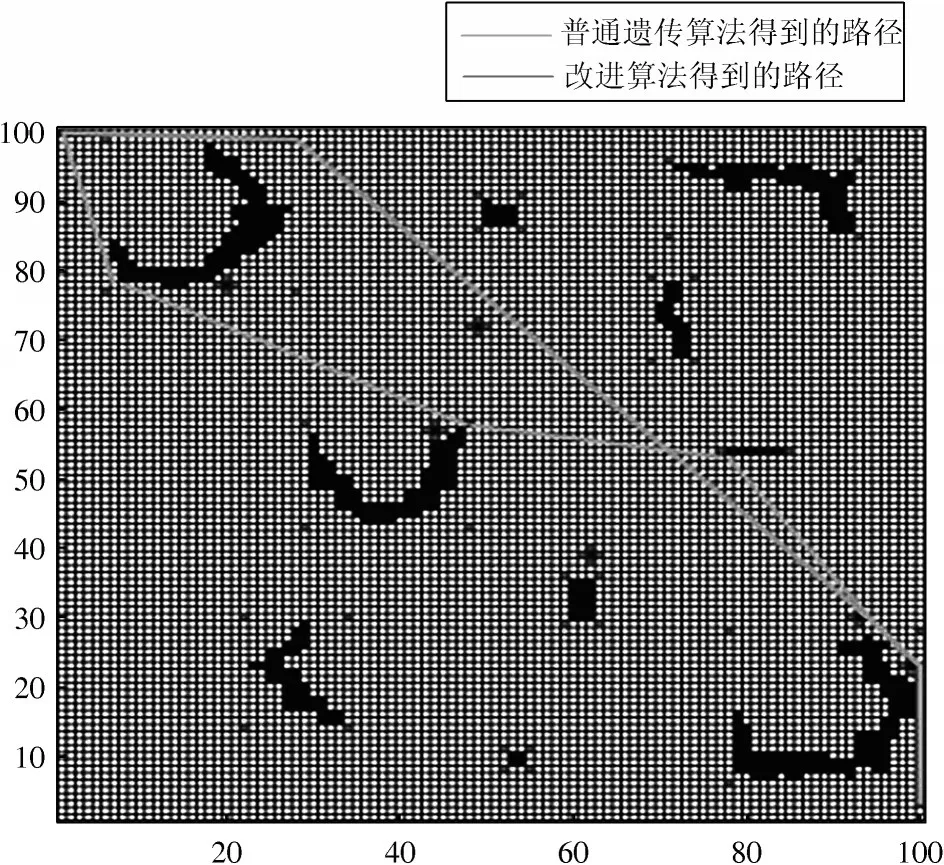
图9 100×100 栅格地图两种算法路径

图10 为迭代次数与距离的收敛曲线。由图10 可知，迭代次数为50 次，随着迭代次数的增加，曲线收敛越快，寻找到的路径距离更短，最终找到相对最优的一条路径。

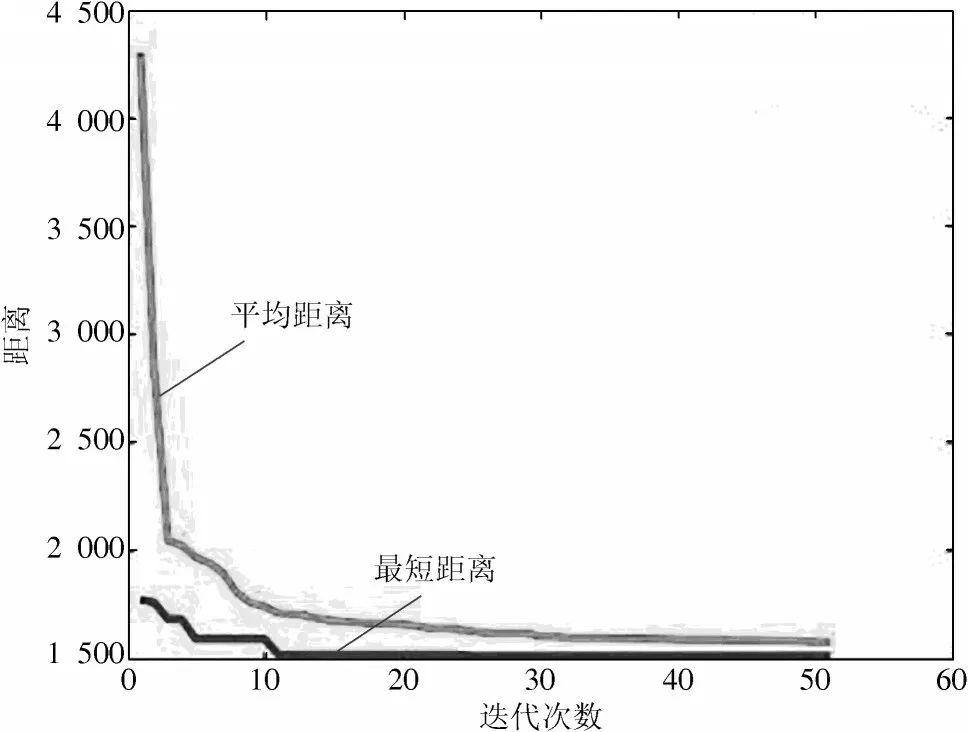
图10 迭代次数与距离的收敛曲线

4 结语

针对AGV 在自动化生产线工作的过程中存在的拐弯节点过多，以及穿墙现象导致与障碍物摩擦的问题，本文通过简化障碍物减少搜索角点，达到简化计算、提高搜索效率的目的；并且改善了栅格地图的坐标系，在一定程度上减少了运用遗传算法时造成的穿墙事件，提高了AGV 的安全性。其次，本文的遗传算法以路径最短为优化目标，且对遗传算法的变异算子进行了改进，并对种群个体进行选择、交叉、变异等操作，不仅找到的路径更短，还能减少路径的拐点数目，使得找到的路径更加顺滑，取得一系列优化效果。

由仿真实验结果可看出：改进算法相对于普通遗传算法来说不仅在一定程度减少了搜索时间，缩短了路径长度，还减少了穿墙次数，有效提高了路径的安全系数；并且通过对变异算子的改进，拐弯角点也有所减少，因此改进算法使规划的路径更加合理有效。但是也存在一些不足，如拐弯处的路径不够圆滑，且无法直观看到耗能量，因此在后续工作会加入节能模型来使算法更加完善。