迭代学习的四旋翼无人机重复航迹跟踪控制实验研究

陈晓雷，仇思超，张开碧，郭 鹏

（1.重庆邮电大学，重庆 400065；2.四川航天系统工程研究所，四川 成都 610100）

0 引言

新工科建设的核心目标是培养高素质复合型新工科人才，其内涵是工程能力的培养，重在实践模式与教学方法改革，让学生学习掌握并具备解决复杂工程问题的能力与方法。清华大学校长邱勇表示，21 世纪的工程教育正在向跨学科交叉、跨领域、跨国家、跨文化合作转变。大学要完善促进学科交叉的体制机制，构建学科交叉人才培养体系，努力培育工程科技领域的创新人才[1]。

目前，我校以强化学生的工程实践与创新能力的思想为指导，推进实验实践教学改革，在人才培养方案中的专业实践创新能力培养和实践培养模式改革中，非常重视对于大学生创新创业能力的训练。基于这样的背景，设计一个以四旋翼无人机为载体的跨学科实践教学平台。四旋翼无人机在飞行过程中具有能够垂直起降、定点悬停等优点，已经被广泛应用于军事和民用领域。精确的航迹跟踪是四旋翼无人机顺利完成指定任务的前提。因此，如何设计航迹跟踪控制算法来提高指定航迹的跟踪精度具有重要的理论意义和研究价值[2]。

四旋翼无人机作为一个欠驱动系统，利用4 个电机提供的输入量去控制6 个输出量，同时各个变量之间存在耦合关系，在实际飞行过程中，还需要考虑到模型参数（如模型质量、转动惯量及升力系数等）的不确定性以及外界的干扰影响（如风干扰）的存在[3]。为了实现四旋翼无人机在其他不确定因素干扰下的精确航迹跟踪控制，需要设计控制器来保证其在外部干扰作用下的稳定性。

1 四旋翼无人机实验平台

四旋翼无人机实验平台由机架和机载电子设备组成。机架是无人机的主要受力部件，要求重量轻、结构强度高、具有一定韧性。实验平台选用轴距为450 mm的尼龙纤维四旋翼无人机机身，如图1 所示。

图1 四旋翼无人机实验平台

该无人机平台在4 个轴臂上各有一个无刷电机，如图2 所示，用于控制无人机姿态及高度。对边方向上的一对电机分别控制无人机的俯仰角与横滚角，对角线上的一对电机控制无人机的航向角，4 个电机同时作用产生的力用于控制无人机的高度。机载电子设备包含Pixhawk 4 飞行控制器、树莓派、GPS 模组等。

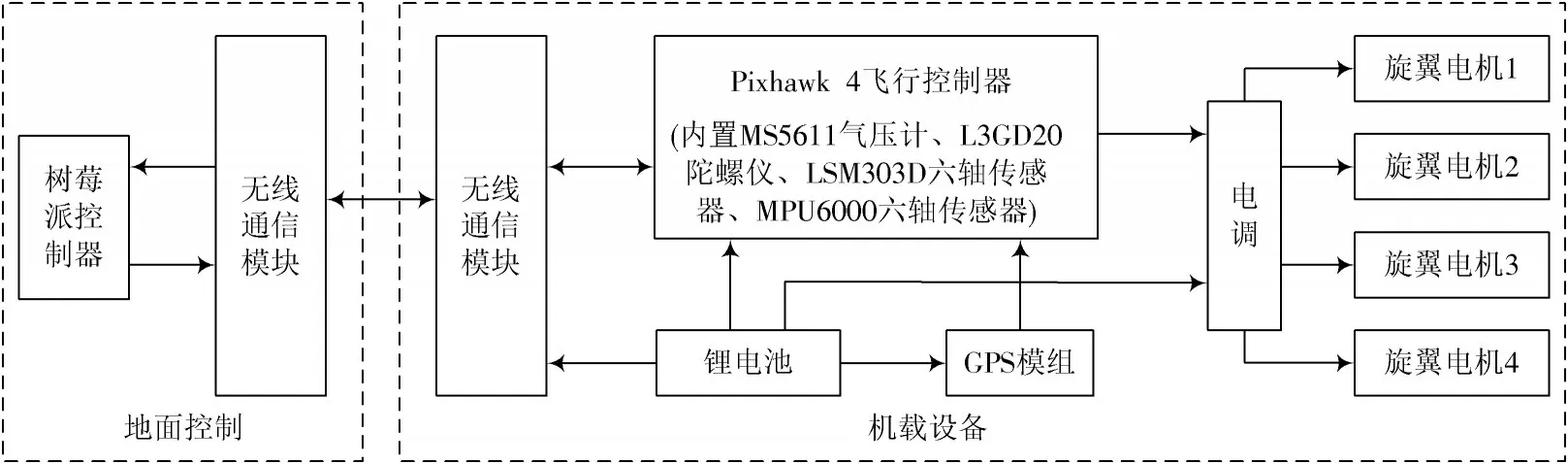
图2 四旋翼无人机硬件系统框图

2 四旋翼无人机动力模型

2.1 四旋翼基础模型

为了对四旋翼无人机进行动力学建模[4⁃5]，定义了如图3 所示的结构图。

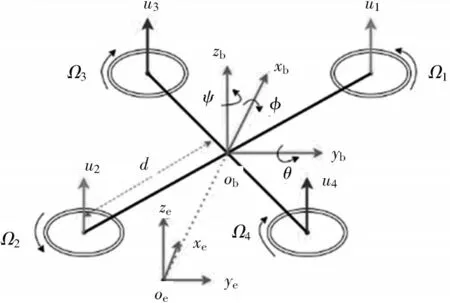
图3 四旋翼无人机结构

对于一个“X”型配置的四旋翼无人机，其垂直运动是通过同时增加或减少4 个螺旋桨转速实现的，螺旋桨（1，4）和（2，3）的转速差会改变横滚角，从而实现左右运动，螺旋桨（1，3）和（2，4）的转速差会改变俯仰角，从而实现前后运动。偏航运动是通过螺旋桨（1，2）和（3，4）产生的反扭力矩的差值实现的。

定义惯性坐标系(oe,xe,ye,ze) 和机体坐标系(ob,xb,yb,zb)，如图3 所示。

向量P=(x,y,z)T和Θ=(ϕ,θ,ψ)T分别表示惯性坐标系下的位置和姿态（横滚角、俯仰角和偏航角），向量ϖb=(p,q,r)T表示机体坐标系下的角速度。

式 中：S*、C*、T*、SEC*分别表示sin(·)、cos(·)、tan(·)、sec(·)。为了便于控制器的设计，假设横滚角和俯仰角的变化很小，则近似为单位对角矩阵。因此，欧拉角速度可以近似等于机体角速度，结合式（1）、式（2）和文献[6⁃8]中的动力学方程，得到四旋翼无人机的动力学模型如下：

式中：m是四旋翼无人机的总质量；g是重力加速度；J=diag([Jxx,Jyy,Jzz])为对角惯性矩阵；Jr为螺旋桨的惯性力矩；Ω=-Ω1+Ω2-Ω3+Ω4，分别对应4 个螺旋桨的转速；kdi(i=1,2,…,6)为阻尼系数；Uz为位置系统的控制输入；Uϕ、Uθ、Uψ分别为3 个姿态角的控制输入。Uz、Uϕ、Uθ、Uψ具体表达式如下：

式中：d为电机到四旋翼重心之间的距离；c=cm/ct，cm为扭矩系数，ct为拉力系数；表示螺旋桨提供的拉力。

利用Pixhawk 4，基于扩展卡尔曼滤波器进行运动数据处理。飞行控制器通过卡尔曼滤波器，将GPS、电子加速度计、电子陀螺仪、电子罗盘、气压计信息测量转换得到的运动数据信息与状态空间方程估算得到的运动数据进行融合，得到更可靠的数据。但该状态空间方程在推导过程中引入了过多的假设，并且是在无人机悬停的条件下建立的，因此该模型在控制飞行器悬停时效果很好。然而，当达到更高的机动速度时，许多额外的因素，例如空气阻力、与环境潜在的相互作用等均会对无人机造成很大的干扰。例如：四旋翼无人机贴近地面时，螺旋桨高速旋转产生的推力作用在地面时，产生的推力会比作用在空气时大许多；环境中风等外部因素会引起更大的影响。大多数控制法则将此类影响视为干扰。在本文中，将采用类似的方法，不对外部干扰进行建模，但在周期性运动的重复执行期间不断地补偿干扰所带来的控制误差。

2.2 控制算法设计

四旋翼无人机控制结构可分为位置环、速度环、姿态环和角速度环四个部分。控制结构图如图4 所示。

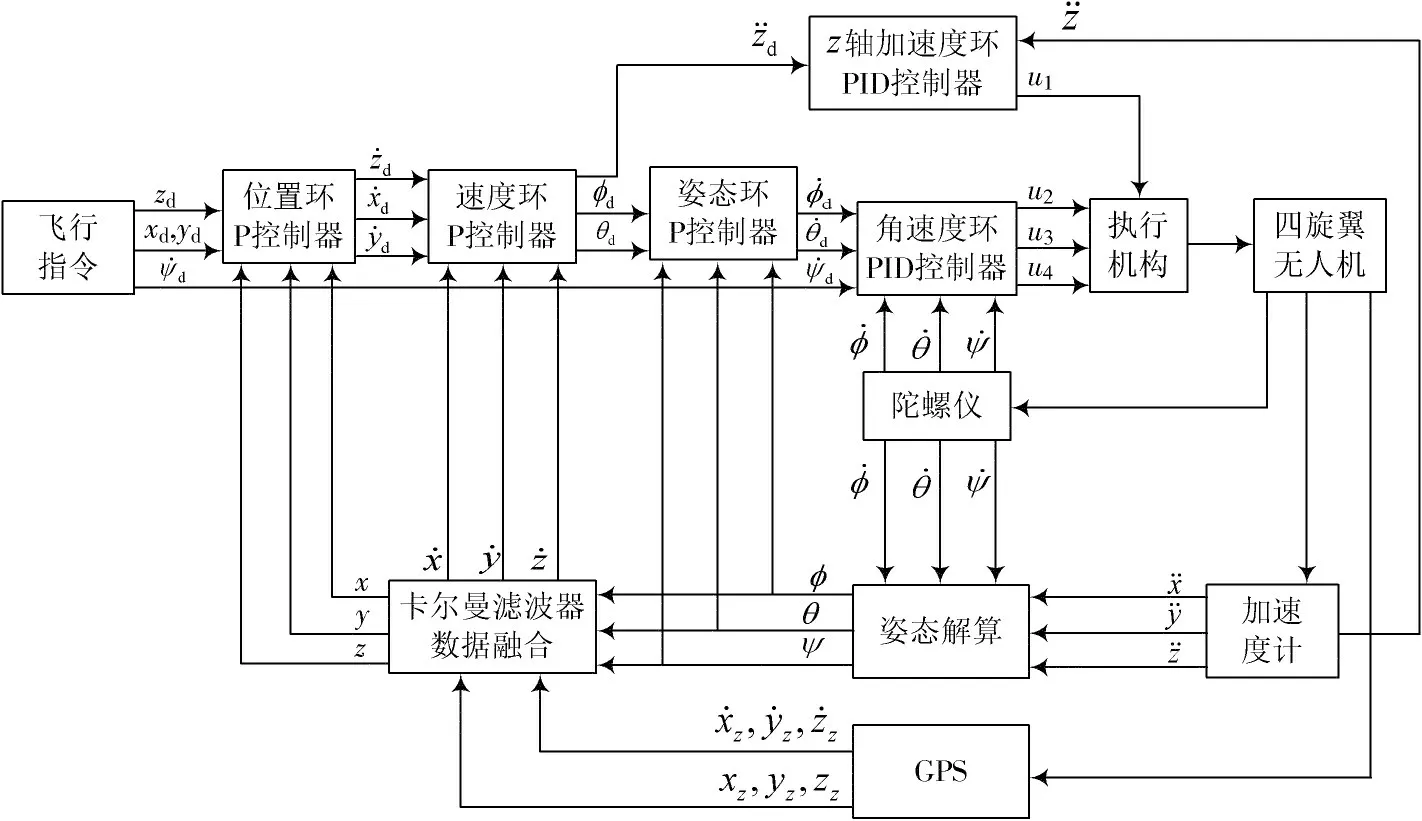
图4 基于串级PID 的四旋翼无人机位置控制结构图

各个环节控制器输入量和输出量对应关系如下。

位置环控制器根据飞行指令给出的期望位置(xd,yd,zd)和数据融合得出的位置(x,y,z)得到期望速度速度环控制器根据期望速度和融合得出的速度得到期望姿 态(ϕd,θd)。姿态环控制器根据期望姿态和姿态解算的姿态(ϕ,θ)得到期 望角速度。z轴加速度环控制器根据期望z轴加速度和加速度计测得的得出对应到电机转速的输出量。期望航向角的角速度由飞行指令直接给出，角速度环控制器根据期望角速度及陀螺仪测量得出的角速度得到对应到4 个电机上的转速输出量。

姿态解算算法负责融合陀螺仪和加速度计测得信息，解算得出飞行器姿态。卡尔曼滤波器负责融合GPS采集的位置信息及运动学建模所得的位置信息。

目前，串级PID 控制算法是应用最广泛的跟踪控制算法。Pixhawk 4 采用串级PID 控制算法进行位置控制，但其只能达到航迹跟踪控制的一般性能，如果要完成对于响应时间要求高的航迹，其控制效果往往不理想。本文通过引入迭代学习控制算法，利用迭代学习控制算法优化串级PID 控制效果。

首先根据所要求的航迹取n个点，定义为[xd(1),yd(1)],[xd(2),yd(2)],…,[xd(n),yd(n)]，再将其与航迹中规定的时间t1,t2,…,tn对应。四旋翼无人机需在tk时间点出现在[xd(k),yd(k)]位置上。

在t=tk时刻，定义系统的输出误差为：

式中：[x(k),y(k)]表示实际tk时刻，四旋翼无人机的实际位置；[ex(k),ey(k)]表示期望位置与实际位置的误差。迭代学习控制的目标是让四旋翼无人机跟踪重复的航迹，在周期内，通过有限次数的迭代学习[9⁃11]最终实现对预期轨迹的跟踪。基本的迭代学习控制算法流程如图5所示。

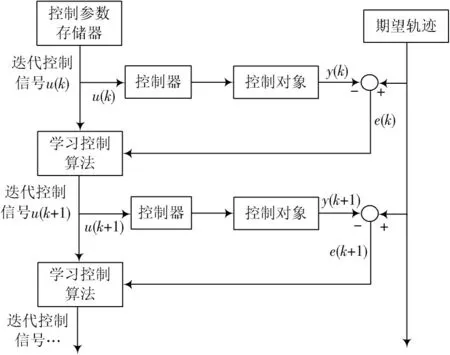
图5 迭代学习控制算法流程

迭代学习控制算法部署在四旋翼无人机上的控制框图如图6 所示。

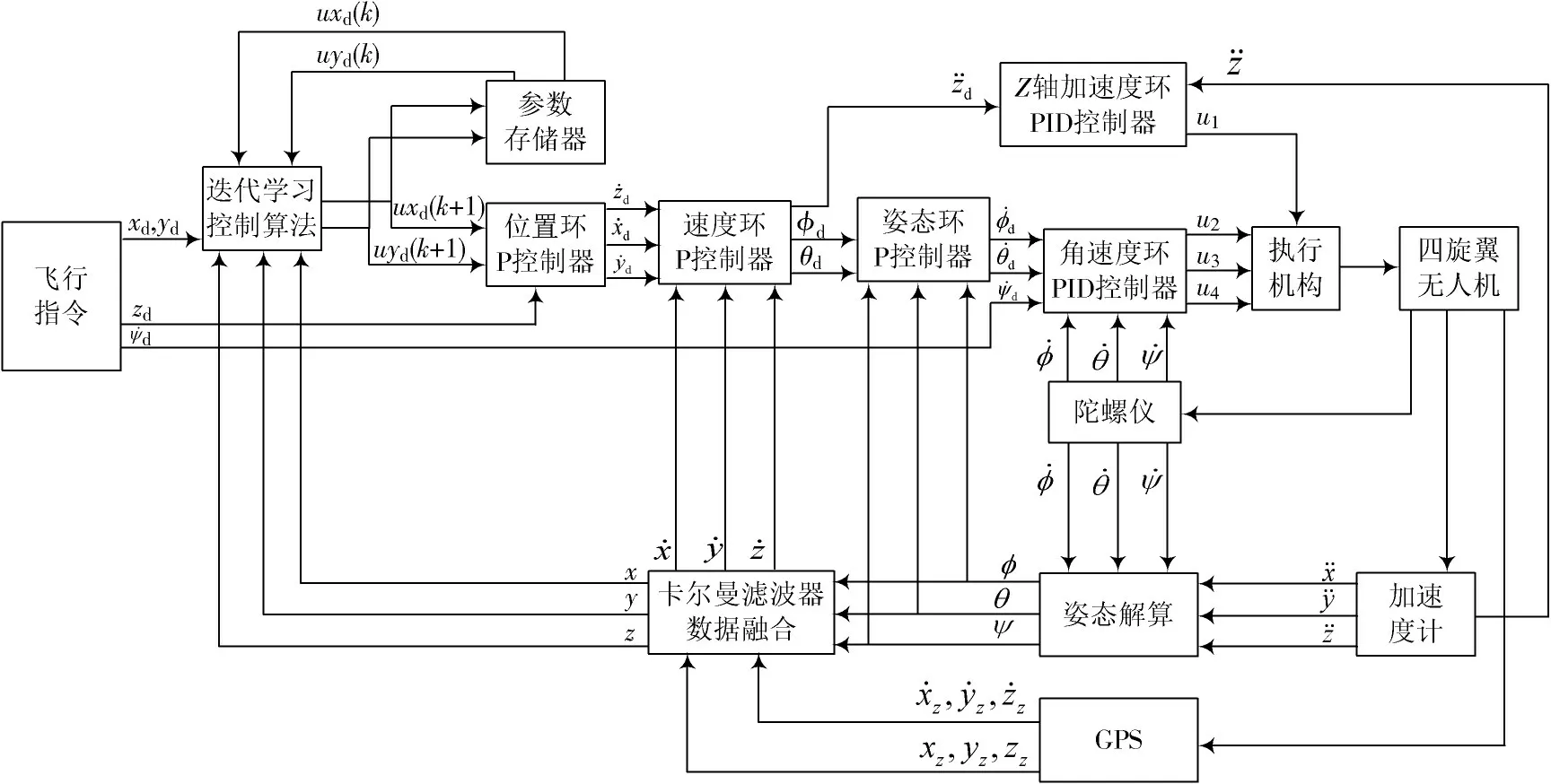
图6 迭代学习控制部署在四旋翼无人机上的控制框图

在现实飞行环境中，高机动情景下，四旋翼无人机的轨迹控制受难以建模的空气阻力影响显著。但是迭代学习控制算法不依赖于精确的数学模型，可以忽略上文建立的运动学模型因未建模空气阻力所造成误差产生的影响。

对于这类扰动，在迭代学习控制算法中，每次飞行周期中基本不变的外部干扰（如风向与风力等级等）在不断迭代的过程中会得到合适的补偿，最终起到消除偏差的作用。

3 仿真结果及分析

本实验基于Simulink 和北京航空航天大学可靠飞行控制组研发的RflySim 无人机模拟器建立四旋翼无人机仿真平台。在仿真平台中，可以观测四旋翼无人机的姿态和飞行航迹。图7 为迭代学习控制仿真原理图。

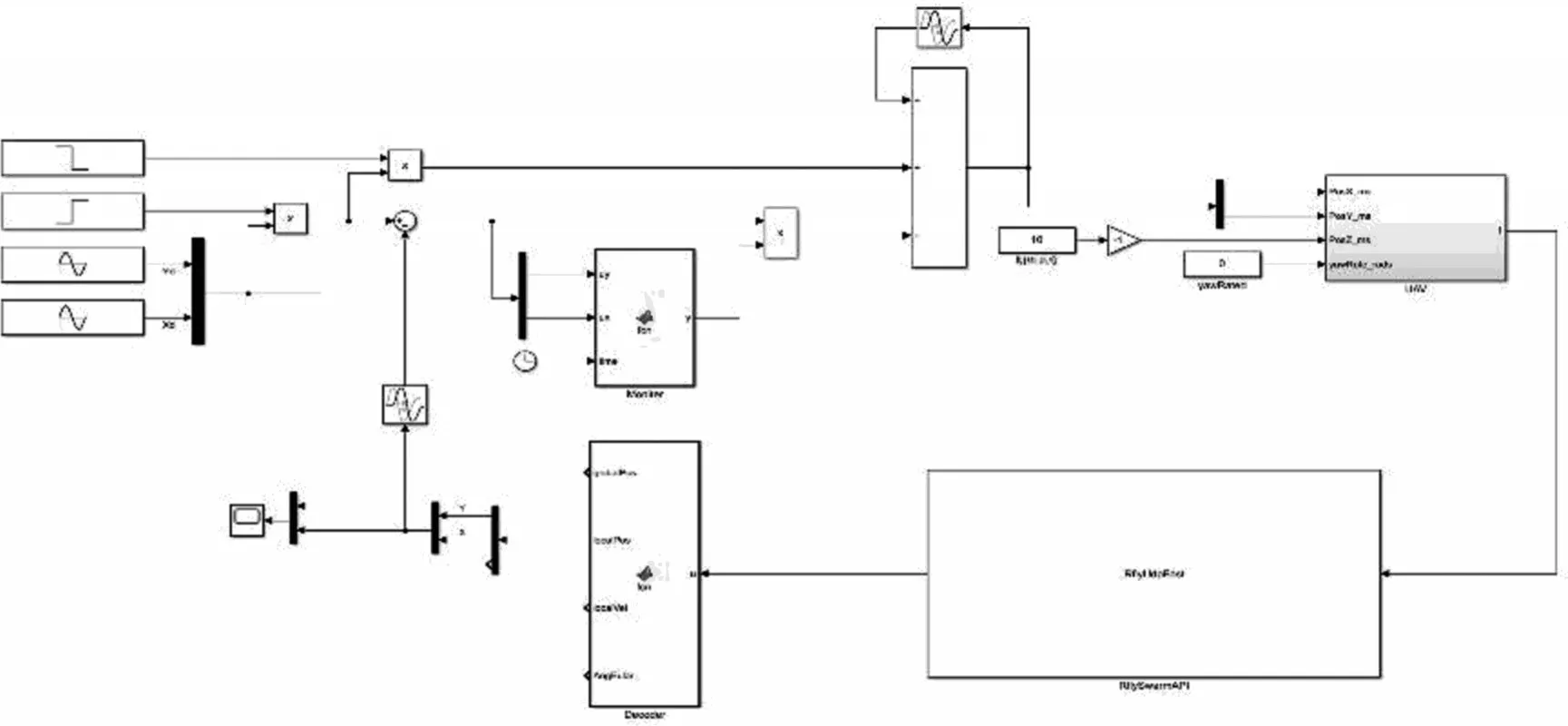
图7 迭代学习控制仿真原理图

干扰条件下“操场形”轨迹跟踪的迭代学习控制效果如图8 所示。干扰条件下，迭代学习控制器需要更多次迭代以适应环境的干扰，最终在位置和时间上均能有效跟踪，实现精准的航迹跟踪控制。对比迭代学习控制优化前后的控制效果，可以得出结论：经过多次迭代学习，系统可以快速补偿外部干扰引起的误差，最终精确地跟踪期望航迹。

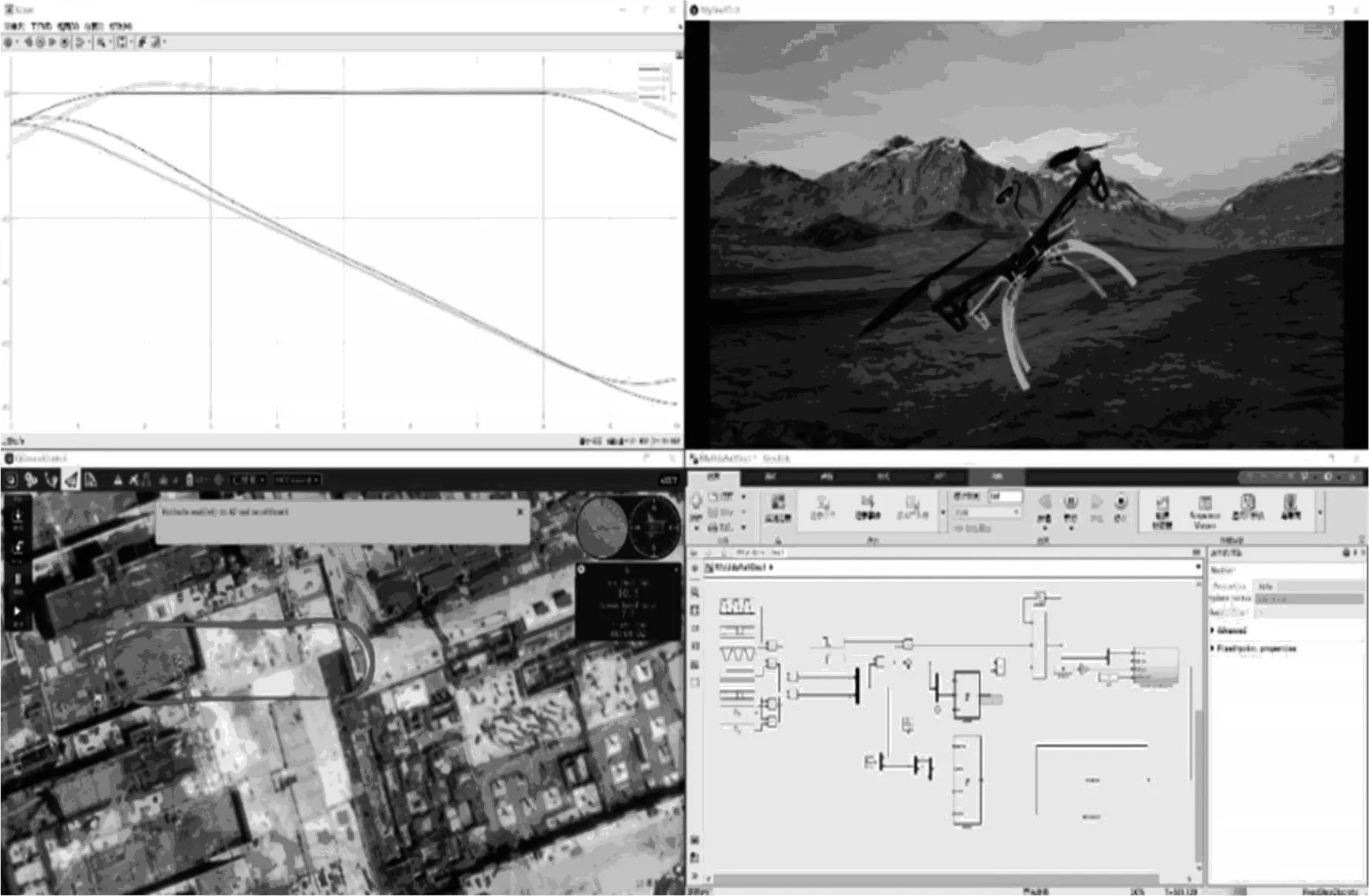
图8 干扰条件下“操场形”轨迹跟踪的迭代学习控制效果

4 航迹跟踪飞行测试

测试时间为2023 年5 月7 日，天气阴，东风转西北风，风力等级3 级，实验地点为重庆邮电大学通鼎实验大楼南部广场，实验中航迹为一个直径10 m 的圆。实验完毕后根据飞行日志，使用日志分析工具Flight Review 可视化本次飞行数据[12]，实验结果如图9 所示。

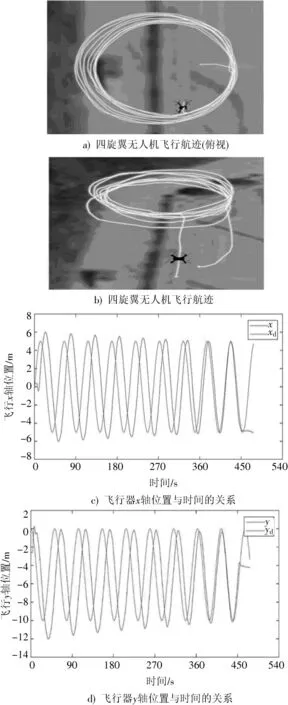
图9 实际飞行测试效果

四旋翼无人机所受主要干扰为自西向东的风。最外圈为串级PID 位置控制用于航迹跟踪的控制效果，可见其受风的干扰严重，偏离期望轨迹。如图9c）和图9d）所示，第一个航迹跟踪周期内，位置控制上存在超调，实际航迹与期望航迹存在时延。但是在迭代学习控制算法的不断优化下，最后一个飞行周期内，四旋翼无人机可以按照规定航迹飞行，位置上逐渐补偿干扰产生的误差，时间上不断接近期望航迹的要求。

5 结语

本文以Simulink 和北京航空航天大学可靠飞行控制组研发的RflySim 无人机模拟器平台为实验平台，以四旋翼无人机为研究对象，研究迭代学习控制算法，掌握算法原理。从优化四旋翼无人机串级PID 位置控制器出发，用迭代学习控制算法对环境中的干扰进行补偿。通过仿真验证算法的航迹跟踪性能，给出四旋翼无人机圆形航迹和“操场形”航迹的跟踪控制结果。最终进行了实际飞行测试，无人机飞行测试结果符合实验的预期，航迹跟踪准确，控制系统并未发散且能逐渐适应外界的稳定干扰。