矩形单元声场波函数构造及其应用∗

贺佐潦霜 向 宇 石梓玉 陈岩豪 陆 静

(1 广西科技大学 广西汽车零部件与整车技术重点实验室 柳州 545006)

(2 广西科技大学机械与汽车工程学院 柳州 545006)

0 引言

在振动结构的辐射声场计算中，边界元法(Boundary element method,BEM)是一种被广泛使用的计算方法[1-2]。通常使用的边界元法包括直接边界元法(Direct-BEM)[3]和间接边界元法(Indirect-BEM)[4]，其在计算声源外部辐射声场时，由于需要数值积分的计算，因此计算效率较低，而且当积分面与振动体表面重合时，会产生奇异性问题[5]，需要使用额外的数值技术解决[6-7]。若将积分面设置在振动体内部(用于求解外问题)或者外部(用于求解内问题)的一个虚拟表面上，即可避免奇异积分的处理，这种方法被称为波叠加法(Wave superposition method,WSM)[8-9]或修正边界元法(Modified BEM,MBEM)[10-11]。该方法避免了奇异积分的处理，但在求解振动体辐射声场时仍需对离散单元进行数值积分计算，当离散单元数量较多、求解规模较大时，单元的积分计算会耗费大量时间。

WSM 中的数值积分来自于对面源辐射声场的计算，若将其用单极子点源代替，则可以得到一种无需积分的高效率计算方法，即等效源法(Equivalent source method,ESM)[12-13]。但ESM 中的单极子点源是对面源辐射声场的过度简化，其计算精度和稳定性较大程度依赖于等效源位置和数目的选择。针对以上问题，相关学者提出了优化等效源配置[14-15]、采用具有指向性的射线波函数来代替单极子点源[16-17]等方法，并取得了一定的研究成果。但在面源简化为点源的过程中，始终存在较大积分近似误差[11]，一定程度上影响了计算精度。

针对上述缺陷，本文根据外问题中声源产生的空间声场，总可以展开成一系列不同阶次的球Hankel 函数与球谐波函数乘积的加权和[18]，构造了一种波函数替代WSM中Green 函数在单元区域的积分，避免了在求解振动体外部辐射声场中复杂的积分计算。以矩形常数单元为例，推导了替代矩形单元积分一般形式和内推形式的波函数，以及当离散单元为正方形时，可将波函数进一步简化为圆形域内推波函数。文中对比了几种波函数与直接积分的计算精度和计算效率，并通过简支板声源和立方箱体辐射声源的数值仿真算例，验证了圆形域内推波函数与ESM在声场计算中的效果。

1 波叠加积分方程及其离散形式

根据WSM 理论，振动体外部r处的辐射声压可以利用式(1)计算：

其中，S′为振动体内部的一个封闭虚拟曲面，q(rE)为虚拟面S′上rE处的源强，G(r,rE)为自由空间Green函数：

其中，|r-rE|为场点r与虚拟面上rE处之间的距离，k为波数，i=

若将虚拟面离散成N个单元，式(1)可写为

当离散的单元足够小时，可以将每一个单元的源强qi(rE)均视为常数qEi，式(1)变为

其中，qEi为i个单元的源强。式(4)就是常用的WSM，该方法虽然计算精度较高，但其在计算振动体外部不同场点r处的声压时，需要对所有单元计算Green 函数的数值积分，导致整体的计算效率较低。

一种更为简化的方法是用振动体内部若干个不同源强的等效源产生的声场，代替振动体辐射的声场，即将单元积分(面源)直接简化为点源G(r,rEi)，得到在声学计算中广泛使用的ESM：

其中，rEi表示第i个等效源的位置，q(rEi)为第i个等效源的源强。

ESM 由于形式简单且无需积分，因此计算效率相较于WSM 得到了很大提高。但该方法对物理模型过度简化，只有当等效源点位置和数目合适时才可达到较高的计算精度，并且从面源简化为点源的近似过程始终存在较大的积分误差，影响了计算精度。

针对上述两种方法缺陷，为了尽可能减小积分近似误差，提高振动体外部辐射声场计算效率，本文采用波函数来代替离散单元的数值积分。

2 矩形常数单元的波函数构造

2.1 矩形常数单元的波函数构造

在工程实际中，对于平板或圆柱等结构的外部辐射声场求解，可采用WSM 设置规则的虚拟平面或圆柱面替代实际声场，这种虚拟曲面通常可以被划分为矩形单元；在近场声全息中，如果使用常规的平面矩形或正方形阵列，为了共形，也可将虚拟面划分为矩形单元。因此本文主要考虑离散单元为矩形时的波函数构造。

在单元局部球坐标系下考虑一个矩形单元的积分，将该单元记为S，如图1所示。其中，单元的局部坐标系的原点位于单元质心ξ，坐标系的x轴和y轴分别平行于矩形两边，将这两边的长度分别记为Lx和Ly。在单元区域内对Green 函数的积分可用一个函数K(r,θ,ϕ)代替：

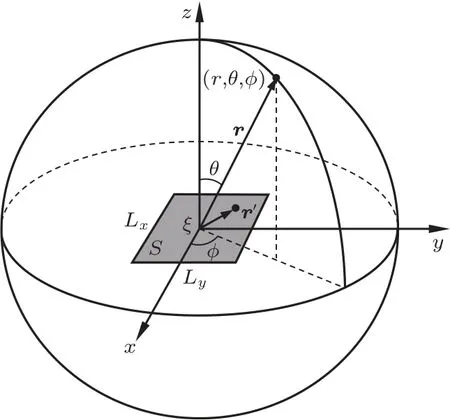
图1 矩形单元S 及其外域球面示意图Fig.1 Schematic diagram of rectangular element S and its outer sphere

其中，(r,θ,ϕ)表示场点在坐标系的位置，r为矩形单元中心ξ到场点的距离，θ为对应俯仰角，ϕ为对应方位角，r′为单元内部的场点。

由于式(6)是一个空间中的辐射声场，因此，可以利用Helmholtz方程在单元局部球坐标系下的解将函数K(r,θ,ϕ)近似为如下的波函数形式：

其中，Cnm为球面波展开系数(kr)为第二类n阶球Hankel 函数，k为波数，(θ,ϕ)为n阶m次的球谐函数，它决定了声压在不同角度的辐射属性，其表达式为

一旦确定了展开系数Cnm，矩形单元的辐射声场也就随之确定了。又由于单元积分和波函数K(r,θ,ϕ)都满足Helmholtz 方程和Sommerfeld 辐射条件，因此根据微分方程的定解理论，只要两者在某一边界上等价，那么它们在整个空间中的声场分布都是等价的。

为计算展开系数Cnm，在单元的外域任选一个半径为R的人工边界球面。则该人工边界上的声场分布为

其中，R是人工边界球面上的点。由球谐函数正交归一性，将式(9)与式(7)联立，即可求出展开系数：

式(11)可进一步表示为全场坐标变量形式：

其中，|r-r′i|为场点r与单元中心点之间的距离，zi为第i个单元在局域坐标系中z轴方向的单位向量。

由于式(11)中人工边界球面是任意选取的，因此本文把该式构造的波函数K(r,θ,ϕ)称为矩形域一般形式波函数。但从式(10)可以看出，在计算展开系数Cnm时需要求解四重积分，因此，当虚拟面离散的单元不一致且数目较多时，将花费大量时间计算展开系数。为缩短计算展开系数Cnm的时间，本文考虑用矩形单元的远场辐射声压解析解代替单元数值积分。

2.2 矩形域内推波函数的构造

若将人工边界位于远场，即人工边界球面的半径RF远大于单元尺寸。此时，矩形单元的格林函数有近似解析表达式：

其中，(kx,ky)=(ksinθRFcosϕRF,ksinϕRFsinθRF)。将式(13)代入矩形单元积分可得

其中，sinc(x)=sin(x)/x。将式(14)代入式(10)可得

其中，dΩRF=sinϕRFdθRFdϕRF，同理，将式(15)代入式(7)可得

式(16)可进一步表示为全场坐标变量形式：

由于式(16)选用的人工边界位于远场，因此本文把该式构造的波函数KF(r,θ,ϕ)称为矩形域内推波函数。由式(15)可见，当选用远场人工边界时，仅需二重积分即可求出展开系数Cnm，而一般形式波函数在求解展开系数Cnm需要计算四重积分。当离散的单元数目较多时，可大幅度缩短计算展开系数的时间，从而提高声场计算效率。当离散的单元为正方形时，本文利用圆形单元替代正方形单元，进一步简化波函数。

2.3 圆形域内推波函数的构造

当离散的单元为正方形单元S时，可用一个中心点相同、面积相等的圆形域近似代替，则有

如图2(a)所示。可以求得，边长为L的正方形单元的等效圆域半径为a=

图2 正方形单元S 的等效圆域Fig.2 Equivalent circle regionof square element S

由于声场关于z轴旋转对称，因此仅在xz平面上用Legendre 正交函数逼近实际指向性函数即可。如图2(b)所示，半径为R(R>a)的球形人工边界上的实际指向性函数分布为(场点rp选在xz平面人工边界上)：

其中，rp=(R,θ,0)为人工边界xz平面上的场点，r′=(ρ,0,ϑ)为单元内部场点。

由于对称性，式(18)可进一步写为

人工边界xz平面上的声场可用Legendre 正交多项式函数逼近展开：

其中，Pn(cosθ)为Legendre函数。利用Legendre函数的正交性可得展开系数：

与式(13)类似，当选用一个远场人工边界RF时，此时圆形单元的Green函数有近似解析表达式：

其中，J1(kasinθRF)为一阶贝塞尔函数。与前述同理，可得到圆形域外部辐射声场的等效波函数为

式(24)可进一步表示为全场坐标变量形式：

由于式(24)的选用的人工边界位于远场，因此本文把该式构造的波函数称为圆形域内推波函数。可以看出(r,θ)是在KF(r,θ,ϕ)的基础上做了进一步的简化，构造了一个与m项无关的波函数。并且，从式(23)可以看出，展开系数Cnm由二重积分简化为一重积分Cn，进一步缩短计算声场的时间。

2.4 三种波函数的计算精度与计算效率对比

由于本文构造的波函数与WSM 类似，离散的单元位于真实边界回缩的虚拟边界上，其声压表达式不仅严格满足Helmholtz 方程，且在真实边界上关于离散结点的声压分布还是严格满足形函数定义的高阶形函数[19]，因而相较于BEM 所需的单元数更少，对于结构和声场较为简单的情况，有时每个波长仅需2 个单元即可。例如，当划分的单元为正方形时，单元的边长L必须小于或等于半波长，即L≤λ/2，也就是kL≤π。因此，本文比较3 种波函数在kL=π/4、π/2、π的情况下与单元直接积分的拟合效果。

为了对比构造的3 种波函数的计算精度和计算效率，算例选用位于xy平面上的正方形单元和圆形单元声源。正方形单元边长为L，圆形单元的半径为a=近场人工球面半径为L，远场人工球面半径为105L，单元中心点与人工球面中心点都位于坐标原点。计算半径为2L的球面声场，计算的场点数目为105个。算例中的积分均采用Gauss-Legendre 积分，其中，直接积分计算单元声场时，每个积分变量使用4个高斯点，计算波函数展开系数时，每个积分变量使用20 个高斯点。值得指出的是，波函数的最高阶数n选择合适与否对计算结果的影响很大。图3 为在kL=π/4、π/2、π 的情况下，不同阶数的矩形域内推波函数对应的重建声压相对误差，其中，相对误差由式(26) 计算：

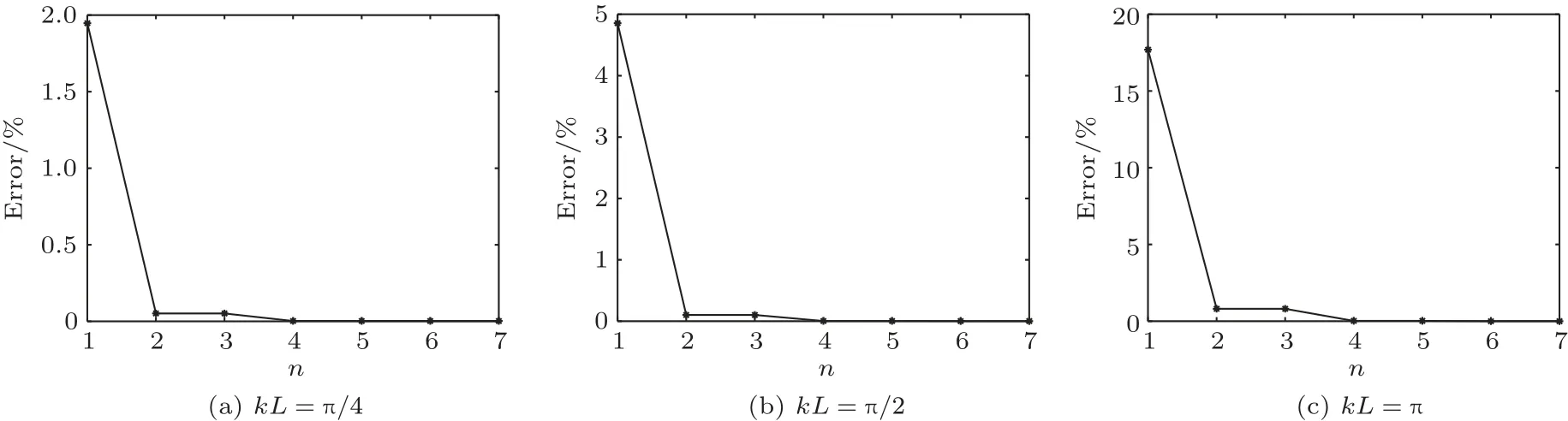
图3 矩形域内推波函数不同阶数对应的重建声压误差Fig.3 Reconstructed sound pressure errors corresponding to different orders of pushwave function in rectangular domain

其中，pn为第n阶波函数重建声压向量，p为直接积分声压向量。

由图3 可以看出，在kL分别为π/4、π/2、π 的情况下，当波函数的阶数n=1 时，计算声压相对误差较大，但随着波函数阶数的增加，相对误差呈下降趋势；当n=4 时，在不同情况下相对误差都小于0.5%，达到了足够的计算精度。

进一步对比3 种波函数在不同情况下的计算精度，表1为ϕ=π/2时，3种波函数在kL分别为π/4、π/2、π 的情况下与单元直接积分的拟合图像与相对误差。当kL分别为π/4、π/2 时，3 种波函数在计算声场声压时，与直接积分的相对误差在0.5%以下，达到了足够的计算精度。当kL=π 时，相当于一个波长内只有两个单元，此时单元内的声场更为复杂。即便如此，矩形域一般形式波函数与内推波函数的计算精度达到了99.5%以上，即便是相对简化的圆形域内推波函数计算精度也能达到98.9%。

表1 kL 分别为π/4、π/2、π 时，3 种波函数与直接积分计算精度对比Table 1 Comparison of calculation accuracy between three wave functions and direct integration at kL is π/4、π/2、π

表2 记录了表1 中kL=π 时波函数与直接积分消耗的计算时间。可以看出，在计算场点声压时，3 种波函数的计算时间均远低于直接积分。但是，矩形域一般形式波函数在求展开系数消耗时间较多，导致总时间还要超过直接积分。因此，这种波函数只有在离散的矩形单元完全相同时，才具有较高的声场计算效率，否则其效率非常低。但采用远场内推之后，矩形域内推波函数求展开系数的时间大幅缩短，其计算速度约为直接积分的4∼5倍，尤其是圆形域内推波函数计算声场的速度是直接积分的12∼13 倍。因此，即便离散单元的形状和大小不一致，内推波函数仍然具有较高的计算效率。

表2 当kL 为π 时3 种波函数与直接积分计算声压的CPU 耗时Table 2 Three kinds of wave functions and CPU time consumption of direct integration to calculate sound pressure at kL is π

为了进一步对比在不同数量场点下矩形域内推波函数、圆形域内推波函数与直接积分的计算效率，设置场点数量从106个增加至9×106个，对比直接积分和波函数所消耗的时间，结果如图4 所示。由图4 可见，直接积分所消耗的计算时间约为矩形域内推波函数的5∼6 倍，为圆形域内推波函数的12∼13 倍。说明波函数的计算效率高于直接积分，且计算的场点数目越多，波函数的优势越明显。

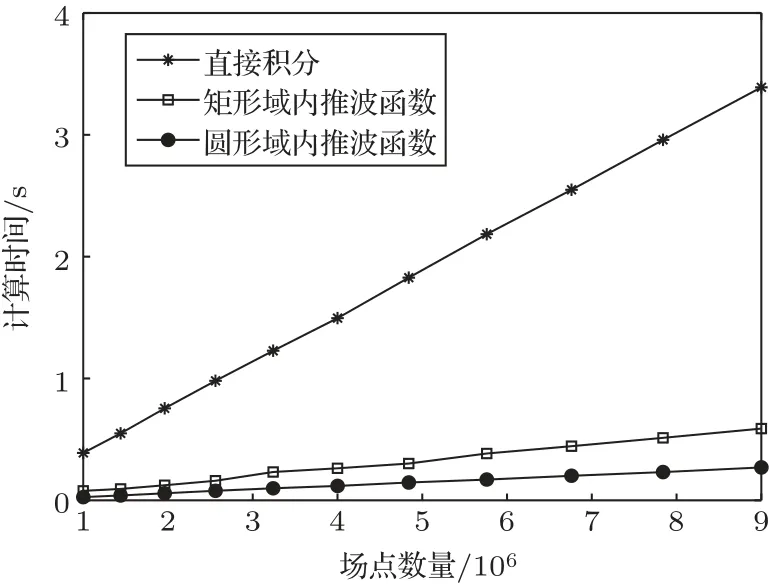
图4 计算不同数量场点声压时直接积分和波函数的CPU 耗时Fig.4 CPU time consumption of direct integration and wave function when calculating sound pressure at different number of field points

3 圆形域内推波函数在声场计算中的应用

3.1 基于圆形域内推波函数的声场计算公式

对于传统的ESM，空间任意r处的声压为

空间任意r处质点速度为

其中，ρ0为介质的密度，ω为角频率。在本算例中，将ESM 中的G(r,rEi)采用3 种波函数中精度相对最低、计算效率最高的圆形域内推波函数替代，考察波函数方法在近场声全息中的计算效果。

与ESM类似，空间任意r处的声压和质点速度分别为

其中，Wi为第i个单元等效波函数的源强。

3.2 圆形域内推波函数在近场声全息中的应用

在实际工程中，板、壳等连续分布的结构振动声源较为常见。因此，本文以四边无限大障板的简支正方形板为研究对象，对比分析圆形域内推波函数与ESM 求解的重建声场。将简支板左下角的顶点作为坐标原点建立坐标系，仿真参数如表3 所示。全息面位于简支板正上方0.03 m 处，均匀分布20×20 个测点。重建面在简支板正上方0.01 m 处，尺寸与简支板大小相同，均匀分布40×40 个重建测点。虚源面尺寸与简支板大小相同，均匀划分为20×20 个正方形单元，单元长度为0.025 m，并用面积相同的圆形域代替正方形单元，在每一个单元中心布置一个等效源点，模型示意如图5 所示。将虚源面分别置于重建面下方0.5倍、1倍、2倍单元长度位置，并在仿真中对全息面测量声压添加信噪比为30 dB 的高斯白噪声，然后对比圆形域内推波函数与ESM重建声场的相对误差。

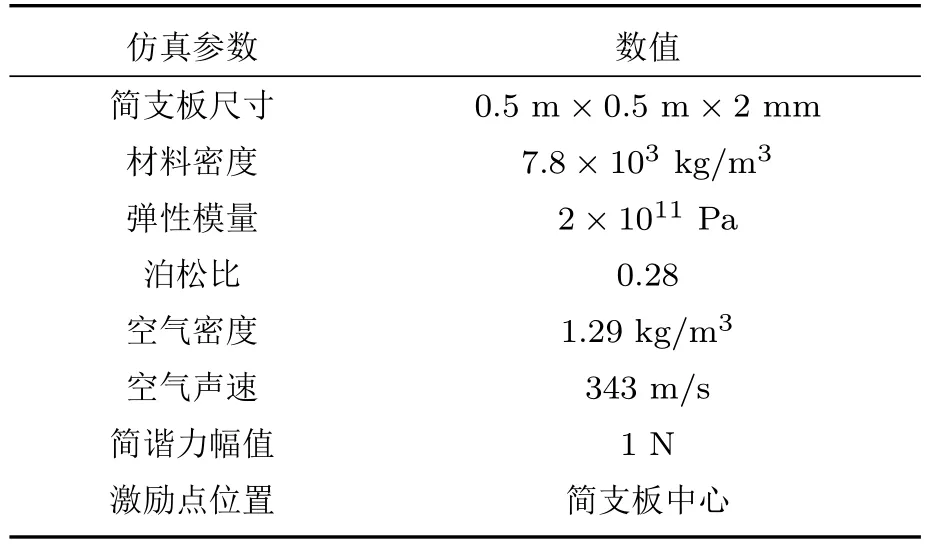
表3 仿真参数Table 3 Simulation parameters

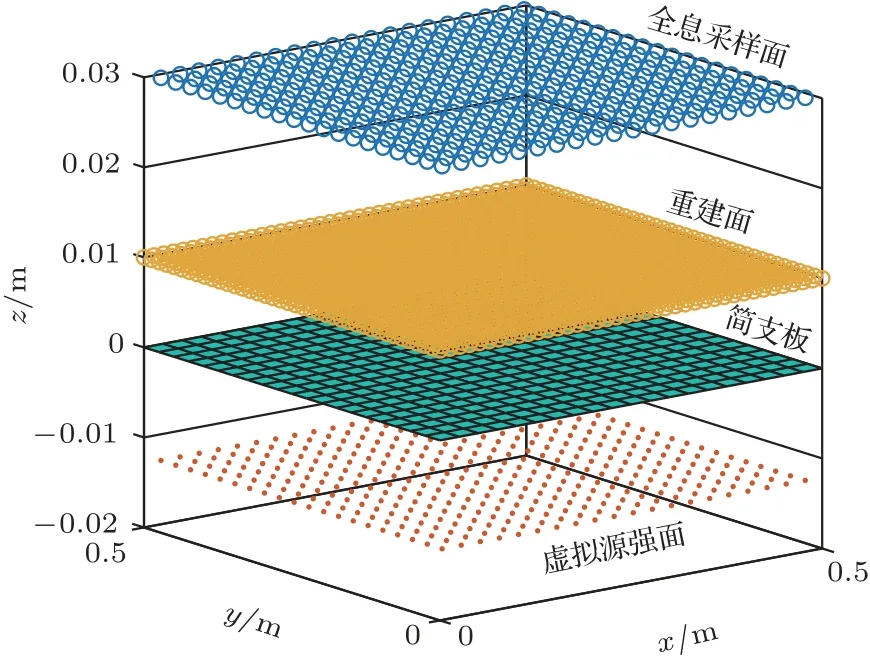
图5 仿真模型示意图Fig.5 Schematic diagram of simulation model

图6 为不同情况下ESM 与圆形域内推波函数重建声压和振速的相对误差，其中，相对误差的定义为

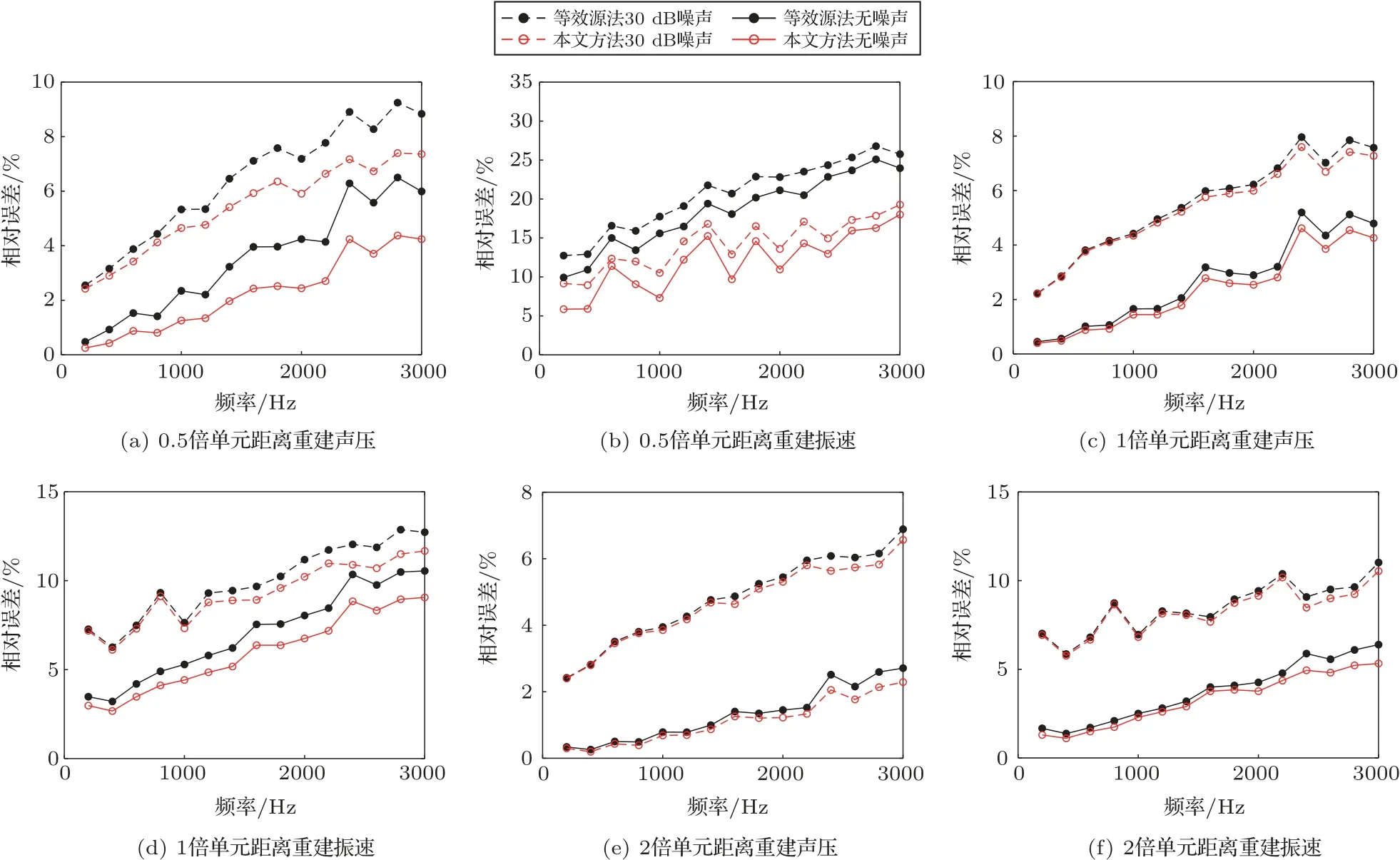
图6 200 ∼3000 Hz 频率下ESM 与圆形域内推波函数重建误差对比Fig.6 Comparison of reconstruction error between equivalent source method and circular domain extrapolation function at 200–3000 Hz frequency

其中，E为重建面的解析声压或解析振速向量，E′为算法重建结果向量。

由图6 的计算结果可以看出，将虚源面置于重建面下方不同距离时，ESM与圆形域内推波函数的声压和振速重建误差均随着重建频率的增加而增大。但在整个计算频段，即便对全息面测量声压添加了信噪比为30 dB 的高斯白噪声，波函数法的声压和振速重建误差也低于ESM，且在虚源面与重建面距离较小时优势更为明显。

3.3 圆形域内推波函数在声辐射计算中的应用

对于无解析解的立方箱体结构，在立方箱体内部放置若干单位源强的单极子源，以这些单极子源在箱体表面单元中心点产生的质点速度作为该箱体的速度边界条件，这些单极子源在单元中心点处的辐射声压则作为标准声压，进一步验证圆形域内推波函数的有效性。

以该立方箱体的中心点为坐标原点，边长为1 m，每面均匀划分为100 个四边形单元，总共600个表面单元。计算时，选取每个表面单元中心点坐标乘以缩放系数进行同形缩放来获得等效源点和圆形单元波函数中心点所在位置坐标(计算时，缩放系数取为0.7)，圆形单元面积为表面四边形单元面积乘以缩放系数。立方箱体表面单元中心点与等效源点、圆形单元中心点如图7所示。

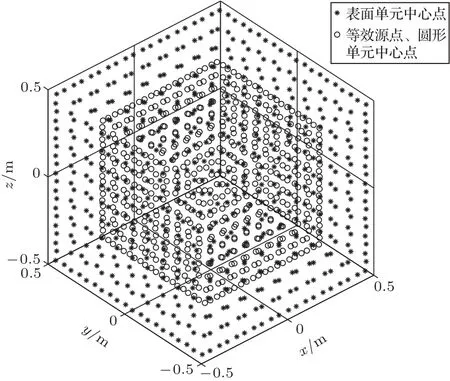
图7 立方箱体表面单元中心点与等效源点、圆形单元中心点示意图Fig.7 Schematic diagram of unit center point,equivalent source point and circular unit center point on the surface of cubic box

算例选用3 个单位源强的单极子点源，分别布置在(0.3 m,0,0)、(0,0.3 m,0)、(0,0,0.3 m)处，声速及介质密度等参数与3.2 节相同。本文对比了200∼1200 Hz频率下ESM与圆形域内推波函数计算立方箱体表面声压相对误差。如图8 所示，当分析频率等于或接近该模型对应的特征频率时，ESM与圆形域内推波函数的计算误差都较大；除特征频率外，两种方法的计算误差都很低，且随着频率的增加而增大。但是，在不同的频率下，圆形域内推波函数的计算误差始终低于ESM。

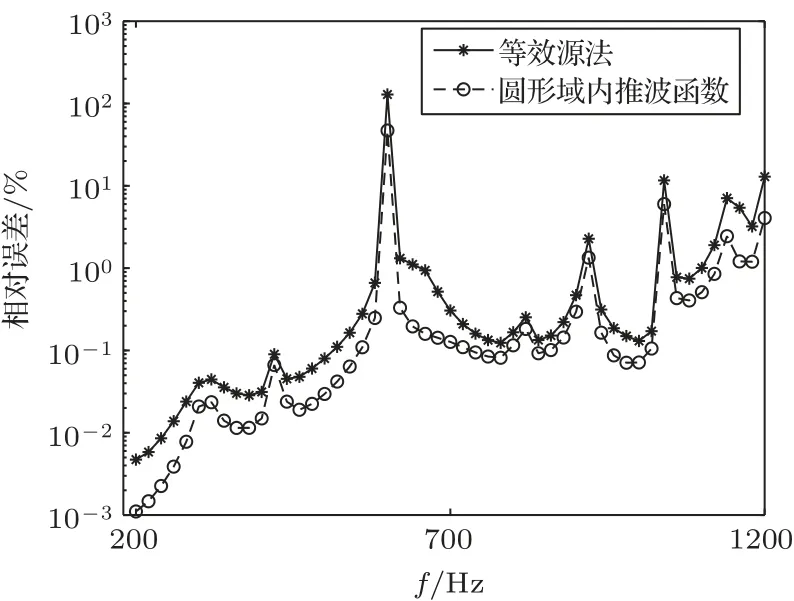
图8 200 ∼1200 Hz 频率下ESM 与圆形域内推波函数计算声压相对误差Fig.8 Relative error of sound pressure calculated by equivalent source method and push wave function in circular domain at 200–1200 Hz frequency

4 结论

为了避免WSM在求解振动体外部辐射声场中复杂的积分计算，本文构造了一种波函数替代单元区域关于Green 函数的积分。并以矩形常数单元为例，推导了替代单元积分的一般形式和内推形式波函数，以及当单元为正方形时的简化内推波函数，并对比了3种波函数与直接积分的计算精度和计算效率。最后，通过简支板声源和立方箱体辐射声源的数值仿真算例，验证了圆形域内推波函数与ESM在声场计算中的效果，主要结论如下：

(1) 在计算单个单元外部声场时，本文构造的3种波函数均与单元直接积分高度拟合，且矩形域一般形式和内推形式波函数的计算效率达到了直接积分的5∼6 倍，圆形域内推波函数的计算效率达到了直接积分的12∼13倍。

(2) 在虚源面划分单元数目、回退距离相同的情况下，即便是3 种波函数中精度相对较低的圆形域内推波函数，在无噪声和加入30 dB 高斯白噪声时，重建简支板外部声压与振速误差仍低于ESM。

(3) 对于内部放置若干单极子点源的立方箱体，在求解箱体表面声压时，当分析频率接近模型的特征频率，ESM 与圆形域内推波函数的计算误差较大。除特征频率外，两种方法的计算精度较高，且在不同频率下，圆形域内推波函数的计算精度显著高于ESM。