高地应力对输水隧洞光面爆破振动传播影响
2024-02-29左依栋
左依栋
(新疆恒诚信工程咨询有限公司,新疆 乌鲁木齐 830000)
随着水利工程建设领域投入的不断增大以及工程技术的进步,我国的水利工程建设逐步向中西部和偏远山区转移。在这一背景下,许多水利工程面临更复杂的地质环境,一些大埋深、长距离输水隧洞面临较大的施工难度[1]。钻爆法是输水隧洞施工中的常用方法,与其余施工方法相比具有施工便捷、成本低等诸多优势。光面爆破技术在20世纪50年代引入我国以来,在岩土工程领域得到广泛应用。该技术不仅能够保证开挖轮廓面的光滑平顺,减少围岩的欠挖和超挖,同时又能有效控制围岩损伤,提高围岩的安全性和稳定性,具有显著的工程效益和经济效益[2]。目前,在水工隧洞光面爆破施工受到各种因素的影响,目前远没有达到预期光面爆破要求,主要原因是对光面爆破机理等问题的认识还不够清晰,特别是在断面岩性等因素变化的情况下,难以对爆破参数进行科学合理的确定和调整。
另一方面,随着计算机技术的不断发展和进步,数值模拟技术已经成为岩土力学研究领域的重要方法。相对于传统的物理模型试验,不仅可以获得较为精确的结果,还可以实现对不易观测或现场模拟的过程进行持续、动态观察,因此在高温、高速爆破过程研究领域具有显著优势[3]。因此,此次研究利用数值模拟的方式,对无地应力、以及双向等值和双向不等值高地应力环境下输水隧洞光面爆破振动传播影响规律进行研究,不仅有利于相关理论的构建和完善,对高地应力输水隧洞光面爆破的施工设计也具有一定的借鉴意义。
1 模型与方法
1.1 模型的构建
在模型构建过程中,结合爆破过程特点和分析计算的实际要求,特作出如下假设:不考虑掘进孔对围岩造成的损伤以及光爆层岩体的破裂和损伤,将影响仅限于周边孔对围岩的损伤;将围岩岩体视为各向同性均质材料,不考虑节理等结构的影响;炮孔内的荷载均匀分布[4]。
鉴于输水隧洞全断面内存在数量较多的周边孔,将全部周边孔纳入模型会导致计算量极大且无必要[5]。因此,研究中选择部分区域进行模拟分析。结合该领域的相关研究成果,当炮孔数量超过4个时,任何一点的峰值速度增加幅度较小。因此,研究中选择5个周边孔进行模型构建和计算分析[6]。
在构建的数值模型中,周边孔直径为40mm,炮孔间距为50cm,轴向长度为50cm,围岩侧深度为3.0m。在模型的网格剖分过程中,充分考虑模型的计算速度和精度,将网格尺寸确定为5cm,同时对炮孔周边部位进行加密处理,整个模型共划分为104350个网格单元,114507个节点。
1.2 边界条件与模型参数
由于此次数值模拟研究需要模拟柱状药包在无限大的岩体内引爆的情况,因此可以将模型简化为平面应变问题进行分析处理,以有效提升计算效率。为了实现对无限大岩体的模拟,将模型的上下和左边界设置为无反射边界条件,起爆方式设置为5孔同时起爆。研究中以Ⅲ级围岩体参数进行计算,采用摩尔-库伦模型进行模拟,其物理力学静态参数见表1。

表1 岩体物理力学参数
1.3 爆破荷载
在爆破施工过程中,炮孔压力曲线是爆炸应力波和准静态气体综合作用的结果,且两个过程相互交织和耦合,难以分离[7]。因此,在模拟计算过程中将炮孔压力曲线分为爆炸应力波和准静态气体2个过程[8]。一般来说,预裂爆破的压力时间大约为数百微妙,裂纹的平均扩展速度为400~600m/s。以此次研究中的炮孔直径40mm,炸药密度300~800g/m,炸药爆速为3200m/s。按照上述要求计算,模型的爆炸应力波荷载峰值取160MPa,升压时间为30μs,降压时间取120μs;准静态气体荷载压力取40MPa,升压时间取120μs,稳压持续时间取800μs。
1.4 计算方案
此次研究首先利用构建的有限元模型探索无地应力环境下岩体爆破振动传播规律,并对比分析有无高地应力环境对保留岩体的实际影响,并研究不同高地应力环境水平和数值方向质点振动水平之间存在的差异。对于高地应力环境再次细分为双向等值和双向不等值2种情况,以最大限度模拟工程建设中可能面临的不同地应力环境。对于高地应力工况,结合工程实际和研究需要,设施不同的应力水平,具体的计算方案见表2。
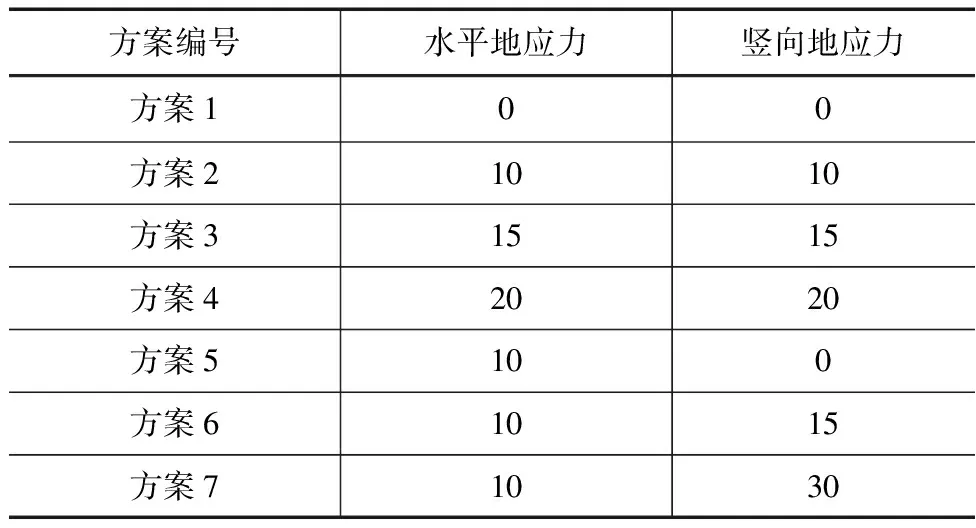
表2 初始地应力设计工况 单位:MPa
2 计算结果与分析
2.1 无地应力
利用构建的有限元模型对无地应力工况的振速和应力进行模拟计算。提取爆心距分别为3、5、7、9、11m等5个典型点位的振速和应力数据进行分析。其中。振速计算结果见表3所示。从计算结果可以看出,随着爆心距的不断增大,振动速度呈现出不断减小的变化趋势且减小的幅度也不断减小。究其原因,主要是在无地应力的环境下,岩体主要受爆炸产生的应力波和爆炸气体的影响而断裂。在炸药药包引爆的瞬间,爆炸冲击波首先作用于炮孔壁,之后衰减为应力波并大部分作用为周边岩体,进而在径向产生显著的压缩应力,而在切向会产生明显的拉伸应力。另外,部分应力波会以渗透波的形式向保留围岩区传递,从而周边围岩区域形成爆破振动区,且随着爆心距的增大,其振动效应也越小。
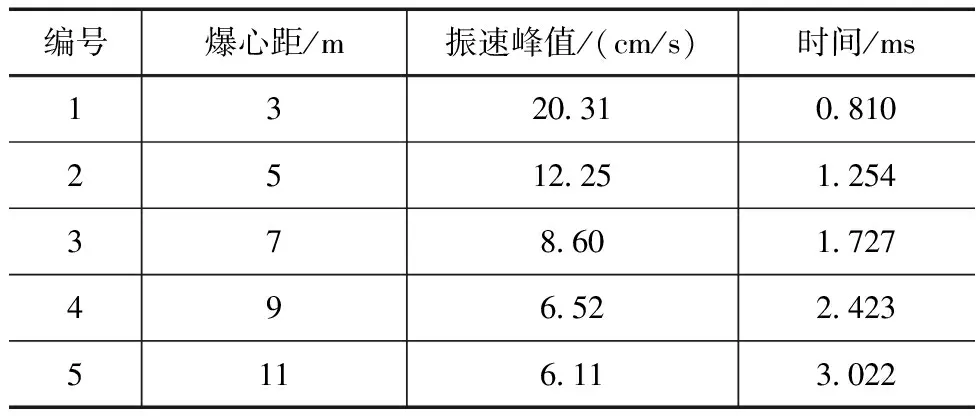
表3 无地应力工况水平振速峰值
在计算结果中提取典型点位的最大有效应力,结果见表4。从计算结果可以看出,随着爆心距的增大,有效应力峰值呈现出不断减小的变化趋势,且减小的幅度也不断减小,究其原因,炸药在引爆的瞬间,其产生的冲击波主要纵波和横波的方式向周边传播。岩体内的各点振动方向与纵波方向一致,与横波方向垂直,随着时间的增长,纵波逐渐传递到远离爆心的一侧,而纵波的应力幅度相对较小,因此有效应力峰值会随着爆心距的增加而减小。
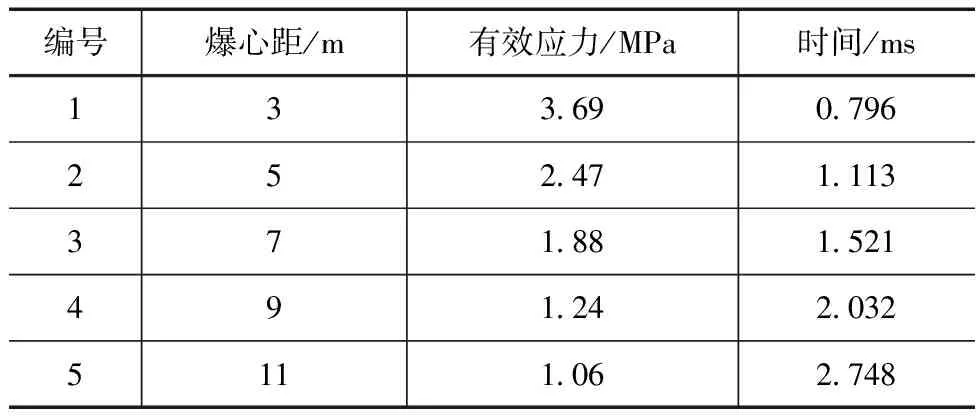
表4 无地应力工况有效应力峰值
2.2 双向等值地应力
利用构建的有限元模型对双向等值地应力计算方案(方案2—4)的振速和有效应力进行计算。从计算结果中提取与爆心距水平距离和竖直距离分别为3、5、7m的6个典型点位(其中水平点位记作X1、X2、X2;竖向点位分别记为Y1、Y2和Y3)的振速和有效应力峰值,结果见表5—6。从计算结果来看,随着爆炸冲击波衰减为应力波,岩体各个点位的爆破振动速度存在相似的变化规律。一方面,无论是水平方向还是竖直方向,爆破振速极值随着爆心距的增加而不断减小,且减小的幅度也不断减小。另一方面,随着地应力值的增大,各个点位的振速极值均呈现出不断增大的变化趋势。由此可见,地应力的大小对爆破振动波具有一定的促进作用,也就是在较大的地应力环境下,爆破开挖过程中的保留围岩岩体将受到更大的振动破坏。从振速的达峰时间来看,随着爆心距的增加,达峰时间也不断增大。另一方面,随着地应力的增大,振速的达峰时间并没有发生显著的变化,虽然存在小幅的波动变化,但是并没有明显的规律性,且变幅十分有限。由此可见,地应力的大小对质点振动速度的传播几乎不存在影响。

表5 双向等值地应力方案振速极值计算结果
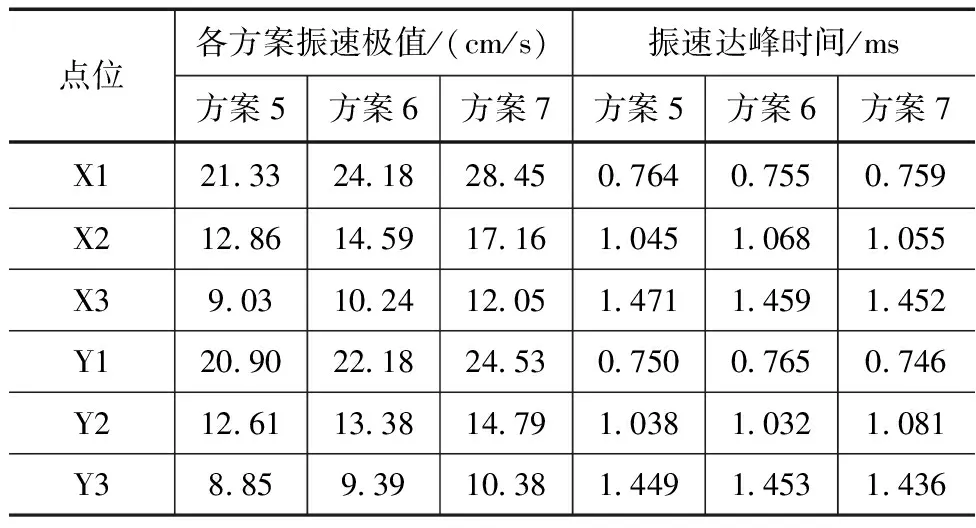
表6 双向不等值地应力方案振速极值计算结果
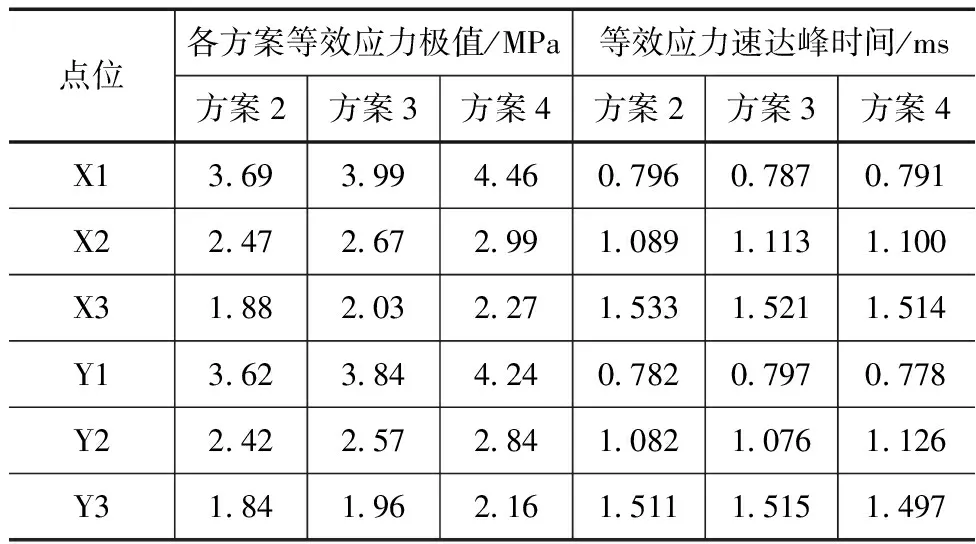
表6 双向等值地应力方案等效应力极值计算结果
从等效应力极值的计算结果来看,也显示出类似的变化规律。首先,等效应力极值随着爆心距的增加而不断减小,且减小的幅度也不断减小。另一方面,随着地应力值的增大,各个点位的爆破应力极值均呈现出不断增大的变化趋势。地应力的大小对等效应力极值达峰时间几乎不存在影响。
2.3 双向不等值地应力
利用构建的有限元模型对双向不等值地应力计算方案(方案5—7)的振速和有效应力进行计算。从计算结果中提取典型点位(与双向等值应力计算方案的点位设计方案相同)的振速和有效应力峰值,结果见表7—8。从计算结果来看,随着爆炸冲击波衰减为应力波,岩体各个点位的爆破振动速度和等效应力均存在相似的变化规律。一方面,无论是水平方向还是竖直方向,爆破振速和等效应力极值均随着爆心距的增加而不断减小,且减小的幅度也不断减小。另一方面,随着竖向地应力值的增大,各个点位的振速和等效应力极值均呈现出不断增大的变化趋势,同时水平方向振速和等效地应力的增加幅度较大,对竖直方向振速和等效地应力极值的影响相对较小。从振速的达峰时间来看,随着爆心距的增加,达峰时间也不断增大。另一方面,随着竖向地应力的增大,振速的达峰时间并没有发生显著的变化。由此可见,在双向不等值地应力条件下,地应力的大小对质点振动速度的传播几乎不存在影响。

表7 双向不等值地应力方案等效应力极值计算结果
3 结语
此次研究利用数值模拟的方式,探讨了高地应力环境下输水隧洞光面爆破振动传播规律,获得了地应力大小对输水隧洞光面爆破振动传播特征的影响,对相关理论研究和工程建设具有一定的借鉴和参考价值。当然,此次研究在建模过程中将围岩岩体假设为各向同性均质材料。但是,天然岩体属于非连续的各向异性材料,这必然会对计算结果的精准性造成影响。基于此,在今后的研究中可以利用自定义材料类型反映岩体的非均匀性特点,以便得到更为精准的研究成果。
