基于沉降差调整闸底板内力计算探析
2024-02-29朱博华
朱博华
(上海诺山工程设计咨询有限公司,上海 200333)
0 引言
倒置梁法是一种近似算法,多用于建在良好土基上的小型水闸。一般是近似地采用“截面法”,将空间问题转化为平面问题的梁或框架进行计算,即通常所说“截板成梁”或“截取框架”的截面法[1]。倒置梁法以截取的单宽板条作为计算对象。至于与闸墩整体浇筑的底板,则把其作为固支于闸墩上的连续梁进行计算,即把闸墩作为底板连续梁的支座,基底反力可按直线分布。倒置梁法没有考虑到基底土的反力不均匀的现实,也没有考虑底板与地基变形协调作用,所以计算出的各闸墩支座处负弯矩偏小,甚至出现小于实际弯矩而导致计算结果偏于不安全。
倒置梁法对地基反力的简化与实际情况不符,是因为基础内力计算中未考虑地基的差异沉降。事实上,在实践中,地基反力是不均匀的,基底反力的分布图形与地基沉降曲线是一致的。因此,反力的简化问题实质上是地基沉降问题。而地基和基础是始终紧密地粘贴在一起,不可能脱离。地基产生沉降,基础必然同时发生位移,基础的沉降差又会产生底板内力。因此,可利用地基的沉降差来调整内力计算,从而对倒置梁法计算的底板内力进行修正。
1 倒置梁法适用条件
1.1 经验判别
倒置梁法是一种简化的计算方法。该方法只考虑了局部弯曲,未考虑沿基础全长的整体弯曲,因而所得的弯矩图正负弯矩最大值较为均衡,基础不利截面的弯矩最小。在实践中,当地基土较为均匀,闸墩距离较小,上部结构和基础的刚度较大时,这样的基础能迫使地基均匀下沉,此时,筏形或条形基础可按倒置梁法进行计算[2]。具体设计时,可依据地基、基础、上部结构等情况,根据工程经验进行判别,见表1。
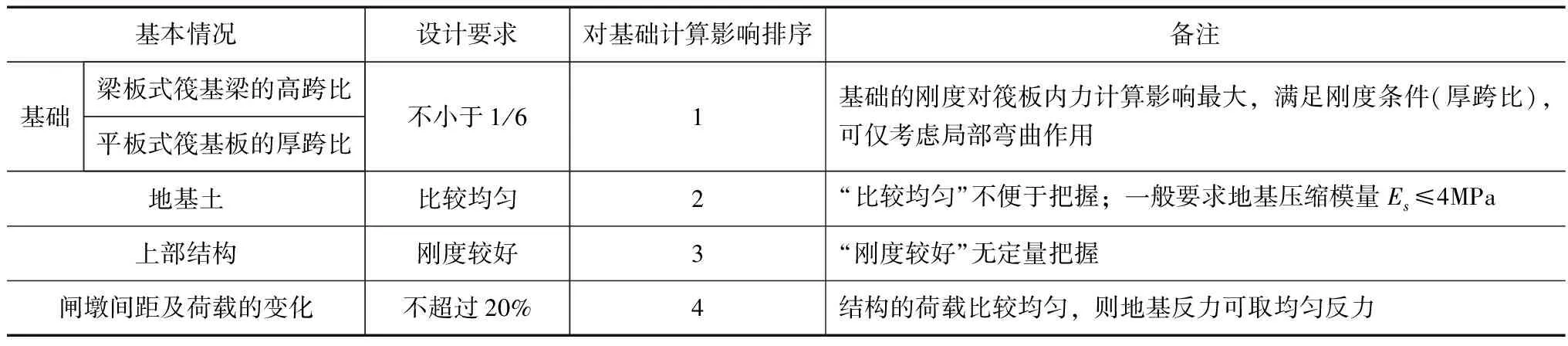
表1 筏形基础按倒置梁法计算要求与分析
1.2 公式判别
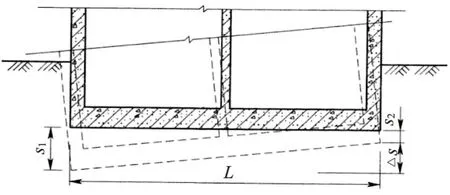
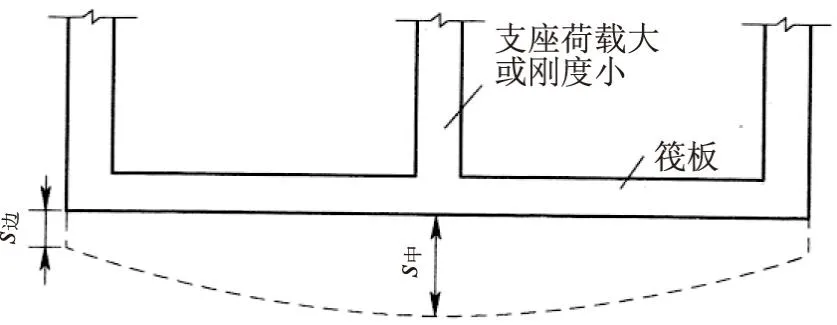
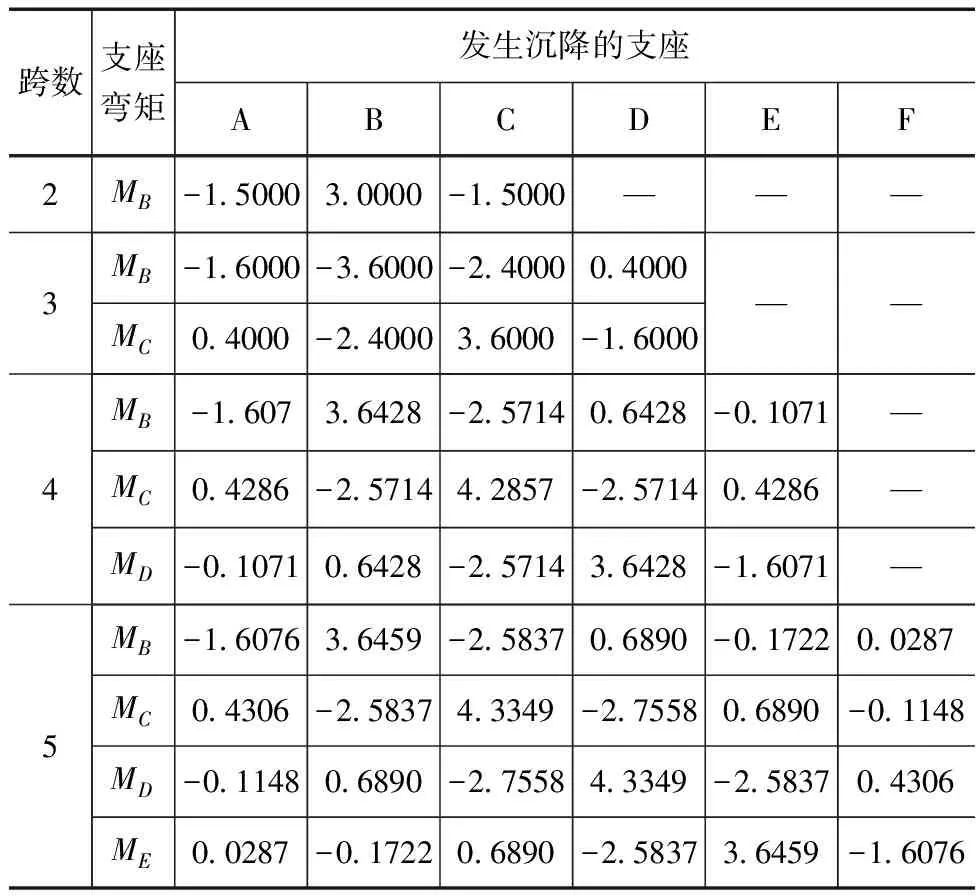
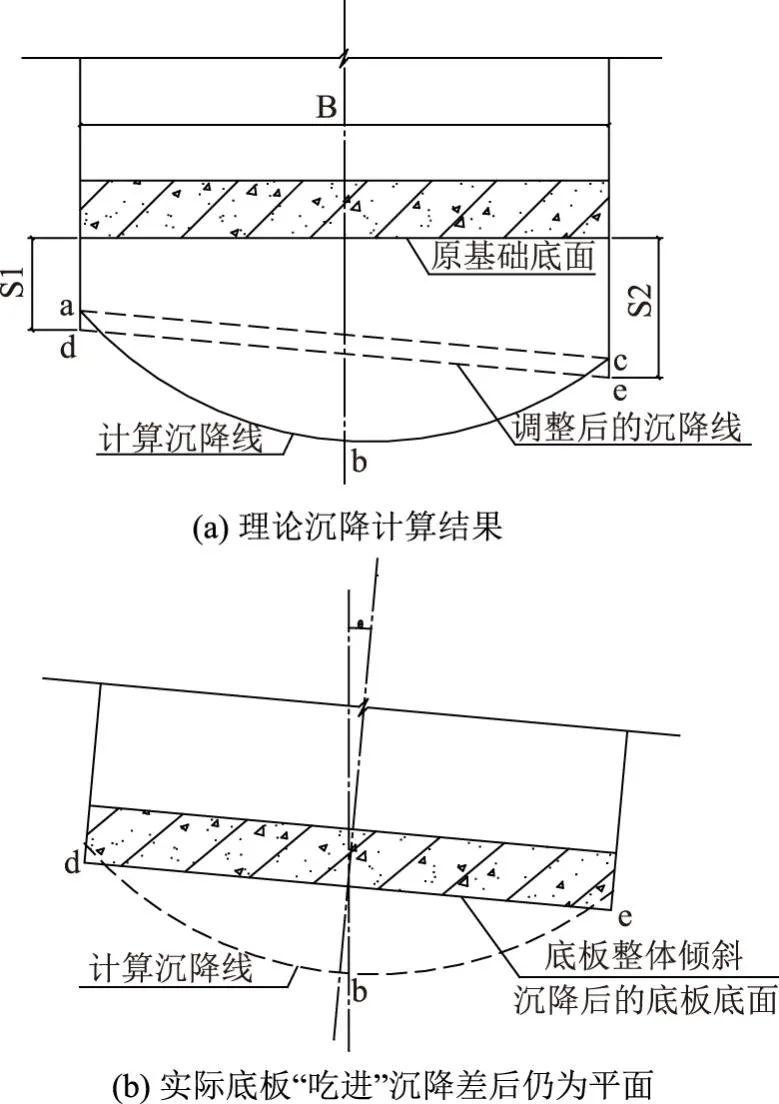
筏基、条基在采用倒置梁法时,都是假定基底反力为直线分布。为满足这一假定,基础要具备足够的刚度,且地基压缩模量Es≤4MPa。压缩模量是另一种表示土的压缩性的指标:Es越小,土的压缩性越高。一般,Es≤4MPa为高压缩性土;4MPa 地基压缩模量对基础的影响。软基上,由于地基的变形模量很小,对基础的约束也就很小。随着地基土变软,基础内力和挠曲均相应增大。反之,当地基土变硬,上部结构对基础内力没有多大影响。 当基础相同时,柔软地基能较好地扩散应力,基底压力分布较均匀。坚硬地基的应力扩散能力较低,基底出现反力集中的现象。因此,压力分布变化较大,尤其当闸墩荷载相对比较均匀,相邻闸墩荷载变化不超过20%时,通常要求基础上的平均闸墩跨距lm应满足条件: (1) (2) 式中,λ—梁的柔度特征值,1/mm,其倒数1/λ称为特征长度;k—基床反力系数,MPa/mm;b—基础梁的宽度,mm;E—梁材料的弹性模量,MPa;I—梁的截面惯性矩,10-12×m2。 λ值与地基的基床系数和梁的抗弯刚度有关。λ值愈小,则基础的相对刚度愈大。对于一般闸墩距及中等压缩性地基,按上述条件进行分析,筏形基础厚度应不小于平均跨距的1/6。当筏基支撑着刚性的上部结构时,筏基则可认为是刚性的,基底反力呈直线分布。 水工建筑多为矩形平板基础,即筏形基础。筏形基础的简化,按不同的假定,可分为刚性板和弹性板。倒置梁法是将筏基视作刚性板,即认为在荷载作用下,基础沉降后,基础底面仍保持平面,地基的反力为线性分布。 事实上,筏形基础都是可变形的,并非绝对刚性。在荷载作用下,筏基的竖向变形,一般可分2部分:整体弯曲变形和局部弯曲变形。筏基是弹性地基上的一块受力复杂的弹性基础板,其变形和地基的沉降是紧密联系在一起的[3]。 地基沉降,既是控制地基承载力的一个关键因素,也是影响基础内力的关键因素,决定了基底压力的分布。理论上,地基的沉降曲线与基底压力图形应是一致的。因此,可以说地基的沉降决定了基础的内力。 2.1.1 基础沉降分析 水工建筑物筏基多为矩形,且尺寸较大。因结构布置需要,决定了基础在2个主轴方向上的刚度有所不同。例如,水工建筑中应用较多的泵房和闸室,由于闸墩的作用不同,导致基础在2个方向上呈现不同的刚度。 根据刚度的不同,基础的变形可分为基础的纵向弯曲和基础的横向倾斜。因此,水工建筑物地基变形计算,应针对基础的纵向弯曲和横向倾斜分别计算地基沉降。当基础均匀沉降时,基础内不会产生内力,而只有在不均匀沉降时,基础才产生内力。 (1)筏基的横向倾斜。水工建筑物平行于水流方向,一般称为纵向。基础纵向因闸墩刚度大,导致基础整体刚度大,抵抗不均匀沉降的能力高。于是,地基发生不均匀沉降时,基底可近似地视为一个平面,即只发生均匀下沉或整体倾斜。基底平面沉降后仍保持平面,中心荷载作用下均匀下沉,基底保持水平。偏心荷载作用下,沉降后基底为一倾斜平面。因纵向基础刚度较大,弯曲微小,对基础内力的影响可以忽略不计。也就是说,地基在顺水流方向上的不均匀沉降,只能引起基础倾斜。 倾斜是指基础倾斜方向上两端点的沉降差与其距离的比值,如图1所示。设计中,只需在计算单元的中轴线上,计算上下游基底下地基的沉降量,基础的纵向倾斜值i计算公式: i=(s1-s2)/L (3) 图1 基础倾斜示意图 式中,i—筏板倾斜值;L—基础宽度,mm;s1,s2—底板上下游边缘中点沉降量,mm。 筏基的倾斜计算是控制不均匀沉降的关键。水工建筑多为整体式基础,上部建筑物多为设备用房,如泵站、水闸等水工建筑物。为保证水工建筑的正常使用,设计时应进行倾斜值控制。 (2)筏基的纵向弯曲。水工建筑物垂直于顺水流方向,一般称为横向。因基础在横向上,闸墩处的刚度比底板的大得多。相对于不均匀沉降,底板会产生局部弯曲。基础纵向弯曲的形状和大小,对基础的内力甚至对上部结构都产生影响。设计中,应在纵向选择有代表性的计算点进行计算。一般,可在底板纵向轴线上,按中墩和边墩的位置选定计算点,分别计算沉降s边、s中,其沉降差为Δs=s中-s边。根据差异沉降,计算基础的横向弯曲。如图2所示,差异沉降,将产生基础内力。 图2 基础整体弯曲示意图 2.1.2 基础沉降计算 水利行业规范中的地基沉降量计算公式,是我国水利工程界常用的分层总和法计算公式。此法需满足3个假定条件:①土的压缩,仅在竖直方向发生而无侧向变形;②土的压缩,是由于孔隙体积的减小,但土粒的体积保持不变;③在土层厚度范围内,压力为均匀分布。该法比较简单,分层计算沉降后叠加,物理概念明确,但计算的工作量相对较大。 地基沉降计算中,分层的厚度适当与否,对计算结果准确与否影响较大。因此,一般,应按以下2个要求确定计算深度和分层。 (1)确定地基压缩层的计算深度zn,按计算层面处附加应力σz与自重应力σcz之比确定,即zn=σz/σcz。在实际工程中,一般,土按σz=0.2σcz,软土按σz=0.1σcz对应的深度zn。附加应力σz可采用角点法计算,但要考虑相邻基础的影响。 (2)为使地基沉降计算更为精确,各计算土层的厚度不宜太厚。分层要求,注意4点:①根据附加压力的分布,基础底面附近分层,厚度应小些;②地下水位处,应是必然的分层面;③不同的土层处,因压缩性不同构成相应的分层面;④由地下水位差异和不同的土层,确定分层后,可再平均划分其中的土层。 2.2.1 计算方法分析 倒置梁法存在2个问题:①地基反力的简化与实际情况不符,而反力的简化实质上是地基沉降;②基础内力计算中没有考虑地基的差异沉降。 针对问题,分析表明,实质上都与沉降对基础内力的影响如何考虑相关。遵循这一思路,研究提出利用沉降差来调整内力计算,对倒置梁法进行修正。依据是地基基础的变形协调,即地基和基础是始终紧密地粘贴在一起,不可能脱离,地基产生沉降,基础必然同时发生位移,而基础的沉降差又会产生内力。因此,可利用地基的沉降差来修正基础内力。 2.2.2 沉降差调整计算内力 在常规的倒置梁法计算的基础上,利用沉降差对其进行修正[4-5],这样可以解决倒置梁法存在的主要问题。沉降差调整计算基础内力分析步骤4个。 (1)根据基础布置,在底板纵向轴线上,按中墩和边墩的位置,选定计算点。采用规范规定的分层总和法,分别计算边墩沉降s边、中墩沉降s中,沉降差Δs=s中-s边。 (2)将沉降差Δs作为支座位移,加到沉降量大的支座上。 (3)计算倒置梁在支座位移差为Δs时梁的内力: M支=β·Δs·EI/L2 (4) 式中,M支—支座弯矩,kN·m;β—支座弯矩系数;Δs—沉降差,m;L—计算跨度,m。 (4)将支座位移产生的弯矩和荷载作用下的弯矩叠加。梁支座编号(从左至右)为A、B、C、D、E、F,梁的计算简图,见图3,β值按照梁的跨数查表2。 图3 梁的计算简图 表2 连续梁支座沉降时的支座弯矩系数表β 2.2.3 调整计算的合理性分析 (1)基础内力计算分析。地基计算,从规范要求和工程实践来看,都是半理论半经验性的计算方法,有时还只能算是一种估算,主要侧重于概念界定和工程经验。基于此前提,对基础的内力计算,还不可能达到精确计算。而利用沉降差进行倒置梁法的内力调整计算,聚焦问题,符合地基基础变形协调一致的原则。因此,采用上述计算方法是具有可行性。 (2)底板“吃进”沉降差。筏形基础为整块大底板,刚性基础,因其自身的挠曲很小,只可能发生整体倾斜。倾斜度以转动角θ表示,计算公式: (5) 式中,B—基础宽度,mm。 理论上,沉降计算的结果是中间沉降量大,如图4(a)所示。刚性基础沉降后,平底基础还是一个平面,基础难以发生“锅形”变形。但计算结果却出现了地基沉降与基础变形的不一致的情况。事实上,在地基的变形过程中,基础底板依靠本身的刚度,“吃进”了中间沉降大所产生的沉降差,如图4(b)所示。由于这部分沉降差被转化为底板内力,因此,可以利用中间沉降大所产生的沉降差,调整计算底板所增加的这部分内力。 图4 理论筏形地基沉降与基础变形 上海市某水闸工程为2孔开敞式闸室[6],单孔净宽8m,闸室采用钢筋混凝土坞式结构,重量轻,整体性好,可承受不均匀沉降,适合软土地基。筏板尺寸为15.0m×18.8m(长×宽)。闸室中墩厚1.2m,边墩厚0.8m。采用天然地基,持力层为粉质黏土,其承载力和地基沉降均满足要求。通过采取倒置梁法和沉降差,调整计算基础内力,进行结构内力的对比计算。 进行结构简化。垂直水流方向,根据上部荷载和结构布置,分别在闸门前后段中间各取1个单宽,视为1个计算单元。假定地基反力在顺水流方向直线分布,地基反力在垂直水流方向均匀分布。作用在底板上的荷载,按规范要求进行计算与组合,选取正常蓄水位情况为计算工况,计算简图,见图5。 图5 计算单元结构剖面(单位:m) 以垂直于水流方向截取的单宽板条作为计算单元,如图5所示。把闸室底板作为固支于闸墩的连续梁进行计算,即把闸墩作为底板连续梁的支座。作用在底板上的荷载、跨度,按前述方法和步骤进行计算,计算简图,见图6。 图6 闸底板倒置梁法计算简图(单位:m) 3.3.1 倒置梁法 作用在底板上的荷载P,按有关规范计算。经计算,P=45kPa,跨中最大弯矩M1=M2=227.8kN·m,支座弯矩为MB=-455.6kN·m;基础弯矩计算结果,见图7。 图7 计算断面弯矩图(单位:kN·m) 3.3.2 沉降差调整计算结果 (1)控制点沉降计算。取底板纵向轴线上的中墩和边墩为计算点,采用规范规定的分层总和法计算。边墩沉降为s边=85mm,中墩沉降为s中=97mm,沉降差为Δs=s中-s边=12mm。 (2)支座位移引起的内力计算。闸室底板为两跨连续梁,为超静定结构。当支座产生位移时,结构中,一般会引起内力。当中墩支座产生位移沉降差,将沉降差ΔS作为支座位移,加到沉降量大的支座(中墩)上,即B点支座多沉降为12mm时,计算支座弯矩MB=-978.3kN·m。将支座位移产生的内力和荷载作用下的内力叠加,即为底板内力。计算结果及对比,如图7所示。 (1)倒置梁法,是假定上部结构为绝对的刚性,即上部结构相对基础刚度很大时,建筑物整体只能均匀沉降,各闸墩之间没有沉降差异,视为基础的铰支座,基础不产生整体弯曲,仅承受基底压力下的局部弯曲。 (2)由于倒置梁法采用“截板成梁”,但在计算过程中,未计算分配不平衡剪力,而且支座反力与闸墩实际的垂直荷载也不相等。因此,有必要对倒置梁法计算的结果进行修正。 (3)地基和基础是始终紧密地粘贴在一起,不可能脱离。地基产生沉降,基础必然同时发生位移,而基础的沉降差又会产生底板内力。因此,可利用地基的沉降差来调整底板的内力计算。2 利用沉降差进行内力调整计算
2.1 基础沉降分析
2.2 倒置梁法分析及调整

3 工程实例
3.1 计算单元
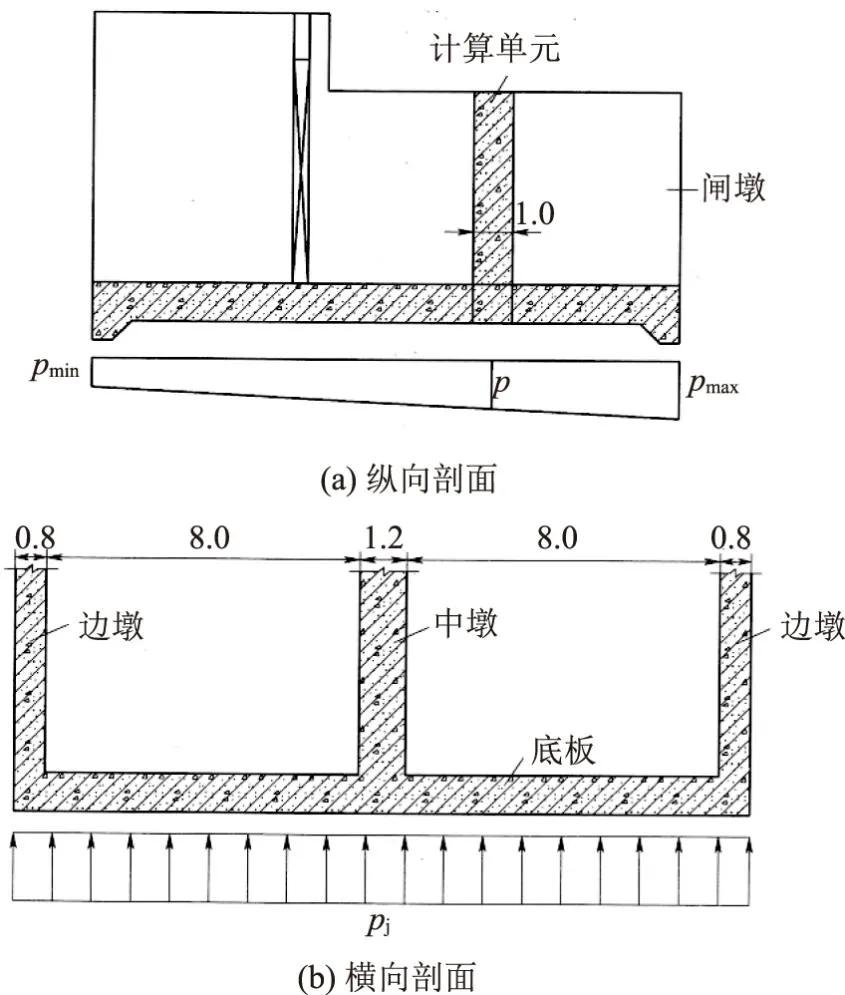
3.2 计算简图
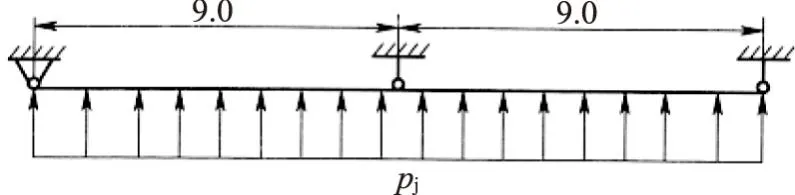
3.3 计算结果

4 结论
