一种ARGB数据无损压缩解压算法的FPGA设计

尹 明，孙国庆

(1.青岛科技大学 信息学院，山东 青岛 266100；2.西安电子科技大学广州研究院，广州 510000)

0 引言

在GPU、AI等芯片设计领域，存储器访问往往是系统性能的瓶颈，提高存储器的访问效率对提升芯片性能的意义重大，其中对颜色缓冲区数据(AGRB)的频繁读写性能的影响很大[1]。从数据压缩算法的角度，通过减少访问颜色缓冲区的数据量来提高存储器的带宽和访问效率[2-3]。

图像压缩是一种通过使用更紧凑的方式来存储和传输图像数据的技术。在进行无损图像压缩时，通常会对图像的各个通道(包括红色通道(R)、绿色通道(G)、蓝色通道(B)以及透明度通道(A))进行处理，这些通道数据通常是基于AGRB格式。数据压缩的原理来自于信息内存在的数据冗余。文献[4]提出一种多级流水的Gzip压缩设计架构。利用并行处理窗口的设计实现数据压缩的并行处理，通过匹配选择消除了并行处理的相关性[4]。文献[5]使用了计算速度与拟合精度更有优势的自注意力机制模型，同时引入字典编码的优势，以字节对编码(Byte-pair Encoding)的形式生成字典，以模型计算数据集统计信息，辅以算术编码AC进行压缩，能够达到吞吐率与压缩比都更高的无损压缩模型[5]。文献[6]提出了一种在FPGA平台上实现Huffman编码以及高速存入DDR3SDRAM存储器的研究方案[6]。文献[7]根据LZ77和LZW压缩算法的基本原理，通过分析多种影响LZ77和LZW压缩性能的关键因素，提出诸如双Hash函数查找方式、并行匹配处理方法、更有效的LZ77数据存储格式、高效数据拼接器以及并行Hash函数查找方式等多种加速方法及其硬件结构，并设计出相应的LZ77和LZW硬件压缩电路[7]。但是Deflate压缩算法有缺陷，Huffman的存储结构也需要进行优化。根据香农提出的信息论中的率失真理论，可以利用这种冗余来实现图像的压缩，即在保持图像质量的前提下，减小图像数据的存储或传输所需的空间或带宽。通过压缩算法和技术，可以消除图像中的冗余信息，包括空间冗余(由于图像中的相邻像素之间的相似性)和统计冗余(由于像素值分布的规律性)，从而实现高效的图像压缩。

对于GPU而言，对图像的访问并不限于整张图片。GPU具有强大的随机访问能力，因此在处理压缩后的图像时，可以仅改变部分区域而无需修改整个图像[8]。为了实现这一点，压缩后的文件需要提供每个压缩区域的位置信息。通过解压缩文件并根据索引找到特定位置，可以修改相应区域的像素数据。为了满足这一需求，开发了一种图像单元的压缩算法，该压缩算法能够对图像的特定区域进行快速压缩和解压缩操作。通过这种压缩算法，能够快速改变图像的特定区域，并且有效减小传输带宽的占用。

1 无损压缩算法的设计思路

1.1 优化Deflate压缩算法流程图

Deflate压缩算法的实现流程如下：

1)通过使用LZ77算法，找到输入数据中的重复片段，并用指针和长度来表示这些重复片段。

2)使用哈夫曼编码对指针和长度进行编码，将它们转换为更短的比特序列。

3)在进行哈夫曼编码之前，还会构建一个动态的哈夫曼树，根据输入数据的频率来调整编码方式，以实现更高效地压缩。

4)将编码后的数据和一些元数据一起打包成压缩数据格式，并输出压缩结果。

通过这一系列的步骤，Deflate压缩算法能够实现对数据的高效压缩，以减小数据的存储空间占用。

将图像的特定区域称为“tile”，并实现了对该区域的压缩和解压缩功能。设置了不同大小的tile，包括4×4、8×8和16×16像素的块，对应的字节大小分别为64、256和1 024字节。主要目的是实现对图片区域的压缩和解压缩，所以每次压缩的数据量并不大，仅限于这3种字节大小。

针对Deflate压缩算法，在进行LZ77压缩之后，如果按照传统方式使用Huffman算法进行压缩，保存Huffman编码表所需的内存空间较大。所以Huffman再对LZ77压缩的结果进行压缩提升的压缩率不明显。为此，对Deflate算法进行了优化，将LZ77和Huffman算法的执行过程并行化，以提高压缩效率[9]。

本算法的流程如图1所示。

图1 该压缩算法流程图

使用v4头部格式的位图文件。v4bmp是一种位图文件格式的扩展，它具有更丰富的信息和功能，特别适用于支持RGBA颜色空间的图像。包含AGRB共4个颜色的通道。对文件的压缩和解压基于此文件展开压缩和解压的。

算法开始之后，对bmp文件的文件头进行读取并保存，获得了图片的高度和宽度，然后按顺序读取所有的AGRB像素数据并保存。再从保存的AGRB数据中读取一个图像区域，对其进行差分预测编码之后再进行LZ77压缩，并且对此图像区域进行Huffman压缩，比较两个压缩算法完成后的文件大小，判断其是否都小于256字节，如果都小于256字节，那么就将其中较小的写入压缩文件，否则就直接把原始的图像区域写入压缩文件，这样可以获得较小的压缩率。

压缩后的文件给出了图像的宽度和高度，以便解压时可以完整地还原原始的图像信息。应该注意到压缩后的文件中的TileCount和DataInfo两个数据，正如之前所说的GPU具有强大的随机访问的性能，在某些领域的图像更改不需要改变所有的图像信息。因此，当某个图像区域需要改变时，只需要知道压缩后其所在压缩图像的位置，将其从压缩后的文件中取出后解压并改变像素数据即可。TileCount和DataInfo便是找到压缩后图像数据所在位置的关键信息，他能够起到索引作用。

1.2 差分预测编码

对于给定的图像，可以将其AGRB数据进行区域划分，主要介绍按照8*8像素的单位进行划分。这意味着将图像划分为许多8*8的小块，如果需要对图像进行修改，也需要按照这个8*8像素的单位进行变动[10-11]。图像划分格式如图2所示。

图2 压缩块示例

每个图像的“tile”，也就是8*8的小块，包含了64个像素数据。按照8*8像素的方式对图像进行读取，这样就可以获取256个字节的AGRB数据。需要注意的是，这64个像素并不是按照顺序排列的，而是按照图2所示的方式进行读取。采取这样的读取方式是因为对于一张图片来说，这样的区域内的像素之间具有较高的相关性。因此，获取并压缩这样的数据单元可以达到较好的压缩效果。在得到一个单元的AGRB数据之后，进行差分预测编码。

差分预测编码的实现：差分预测编码(Differential Predictive Coding)是一种常用的无损压缩技术，用于压缩数字信号和图像数据。差分预测编码的基本思想是通过对信号或图像中的样本进行预测，然后用预测值与实际值之间的差异进行编码。它利用了信号或图像中的相邻样本之间的相关性，将差分值进行编码，而不是直接对原始样本进行编码。

观察到这些数据没有重复项，这意味着在压缩算法中存在很少的冗余。为了充分利用数据的特点，采用了差分预测编码的方法。通过差分预测编码，可以对每个像素值与其相邻像素值之间的差异进行编码。这样可以进一步提高数据的冗余性，并提高压缩算法的效率。差分预测编码是一种算法，在该算法中，通过获取一个像素值后，利用预测方法来预测下一个像素的值。采用了使用上一个像素的值作为本次读取像素的预测，并计算本次读取的像素值与上一次读取的像素值之间的差值。这种方式可以有效地减少数据的冗余性，并实现对图像数据的压缩。通过差分预测编码，引入了更多的重复数据，增加了数据的冗余度。然而，这种冗余度的增加使得压缩变得更加容易。利用这些重复的数据，可以更有效地进行压缩，因为重复的数据可以被更紧凑地表示和存储，从而达到更高的压缩率。

1.3 LZ77压缩算法

Deflate压缩算法是由Abraham Lempel和Jacob Ziv提出，是基于字典的无损压缩算法的基础，也是无损压缩领域中的主流算法。LZ77算法基于字典匹配的原理，通过寻找重复出现的数据序列并用指向其前一个出现位置和长度的指针来表示，从而实现数据的压缩[12-13]。

LZ77算法会先创建一个字典区和待编码区。LZ77 压缩是一个循环迭代的过程，LZ77编码器在字典区查找，直到找到匹配的字符串。匹配字符串的开始位置与离字典区右边的距离称为“偏移值”，匹配字符串的长度称为“匹配长度”。LZ77在编码时，会一直在字典区中搜索，直到找到最大匹配字符串，然后输出一个三元组(off，len，char)，off表示偏移值，len表示匹配长度，char为待编码区第一个等待编码的字符。编码输出为(0，0，A)，接着，文本序列会向前移动，编码输出为：(1，1，A)。文本序列继续前移一位，编码输出为：(0，0，B)。文本序列继续前移一位，编码输出为：(3，1，B)。文本序列继续前移，直到待编码区为空。所以最后的文本输出为：

(0，0，A)，(1，1，A)，(0，0，B)，(0，0，C)，(2，1，B)，(3，1，B)，(5，3，A)

经过上面的编码会发现，实际输入的文本共有9个字节，而输出共有7×3=21个字节，这就会导致压缩后的数据膨胀，并没有实现压缩的功能。以上只是LZ77算法的基本原理，根据以上原理进行了算法的改动。

对于上述的流程可以发现，字典区越长，待编码区的字符在字典区能够被搜索到的概率越高，也就是匹配的概率越高。然而也并非将待编码区的字符全部替换成(off，len，char)合适。因为保存一个off要一个字节，保存一个len要一个字节，保存一个char也要一个字节，这样压缩之后的数据就会变得膨胀。为此，设置一个界限，当len的长度大于2的时候再进行编码，否则进行原样输出。这样一来，压缩的效率会大大提高。

同时，算法所针对的压缩数据也就是一个图像区域，也就是256个字节。倘若再进行上节所讲的字典区为5，待编码区为3的算法压缩，那么很难找到长度大于2的编码。为此将256字节的一部分作为字典区剩余的另一部分作为待编码区，这样就极大地增加了字符被编码的概率。

获得一个tile之后，先将前两个字符设置为字典，然后再到后面的字符中取字符，在前面的字典区查找，如果找得到，那么就保存其off偏移值，len长度，以及字符char。

在这里，定义以下3个uchar(unsigned char，下同)数组：

ucharcomplbuff[256]；

ucharcompsignbuff[256]；

ucharcompslbuff [256]；

其中complbuff储存的是字典区匹配到的字符，compsignbuff是标志位字符，compslbuff是存储len和off的数组。对以上3个数组进行解释，如果待编码区的字符在字典区没有找到，那么就将其保存在complbuff中，并将标志位符设置为0，表示字典区查找不到。如果能在字典区查找到该字符，并且能匹配到的长度大于二，那么就对其保存off和len，并将标志符设置为1，表示能在字典区找到。

1.4 hash表进行对算法进行加速

根据上述的匹配机制可知，如果直接对字典区和待编码区进行暴力匹配，那么算法的复杂度是O(mn)，它的算法复杂度为O(mn)，其中m是待匹配字符串的长度，n是目标字符串的长度。在hash算法匹配之前，也尝试了KMP算法进行加速，但是效果不是很好，而hash匹配函数，可以较好地完成算法加速的功能[14-15]。

Hash加速如下：

依然是使用上面的字符为例，依旧按照上面所述的流程，将字符的前两个保存在hash表中，当待编码区的2过来时，发现hash里面有2，其位置为2，那么待编码区的字符2直接到字典区的2的位置进行匹配，发现匹配长度为1，不能作为LZ77编码的输出，那么将待编码区的2保存在hash表中，数据前移。

继续重复上述的过程，发现字符在字典区没有找到，那么直接将其插入到hash表中。当下一个字符2进行编码时，在hash表中发现其有位置2、3，那么程序会执行以下过程，首先在hash表中找字符2的位置，为2，那么就从字典区的第二个位置找起。字典区的指针向后移动一个位置，待编码区的指针也向后移动一个位置，直到两个指针位置后面的字符不再相等，就停止移动，并退出字符匹配。同时更新hash表。该表表示将待编码区已经被匹配的2，2字符也插入到了hash表中。

对于已经被匹配的字符2，2使用compslbuff []保存其位置2和长度2。并设置标志字符为1，并保存在数组compsignbuff[]中。如果要对其解压，就读取compsignbuff[]数组，如果值为1，就直接读取compslbuff[]两个字节即可，读取的第一个字节为位置，第二个字节为长度。

1.5 对off和len的优化

对于这样的一个字符串，a b a b a b a b a b a b a b a b a b a b a b a b a b会发现如果按照上面的方式进行压缩，那么输出的编码在compslbuff[]的储存为[0，2][0，4][0，8]......这就导致每来一个a，b字符就会输出一个位置和长度，然而匹配的大小为2，这就导致LZ77算法对这样的一个字符无能为力。为此需要对off和len重新设计[16]。

做出如下的改变，使用新的变量jmp和lgth。将压缩后的文件写成ab[0，12]，这个的含义是在字典区的位置为0的字符开始，这样的字符执行了12次。

这样就对于off和len舍弃使用新的变量进行压缩和解压缩的表示。

寻找最长匹配，假如说找到这样的一个序列：

字典区：a b c d e f b c d e f g

待编码区：a b c d e f g h

目前最佳匹配串：a b c d e f

根据前面设定的marethan的大小，发现最佳匹配串大于了morethan的值，那么就将其保存在对应的数组之中。那么待编码区的字符还剩下g h 两个字符，因为其长度小于marethan，那么就会被算法保存在complbuff之中。最终的a b c d e f b c d e f g h a b c d e f g的编码就会变成a b c d e f [5，5]g h [13，5]g h 。中括号前面的5表示距离前面的匹配的字符的距离，后面的5表示匹配长度。会发现，源字符的后7个字符可以压缩成a[8，6]。最终的编码为a b c d e f [5，5]g h a [8，6]，这样压缩后的字符编码会比之前的更小。

之所以会造成这样的浪费是因为算法只关心前面的这个字符，并不关心将这个字符后面的字符作为匹配，为此对算法的另一个步骤就是寻找最长匹配。

当前字符在匹配时产生的匹配长度(简称当前匹配长度)和下一个字符在匹配时产生的长度(简称下一个长度)有以下几种关系：

1)当前匹配长度>下一个长度：

例：当前上文为a a aa b bb c cc当前下文为a a a b bb，当前最佳匹配串：a a a b bb

下一个上文为：a a a b bb c cca下一个下文为：a a b bb，下一个最佳匹配串为 a a b bb

在这种情况下，下一个最佳匹配串的长度小于当前最佳匹配串的长度。

2)当前长度=下一个长度：

例：当前上文为a a a b bb a a b bbc，当前下文为a a a b bbc，当前最佳匹配串：a a a b bb

下一个上文为：a a a b bb a a b bbc下一个下文为：a a b b b c，下一个最佳匹配串：a a b bb c

此时下一个最佳匹配串的长度与当前最佳匹配串的长度相等。

3)当前长度<下一个长度：

例：当前上文为a a a b bb a a b bb c d，当前下文为a a a b bb c d，当前最佳匹配串：a a a b bb

下一个上文为：a a a b bb a a b bb c d a下一个下文为：a a b bb c d，下一个最佳匹配串：a a b bb c d

此时下一个最佳匹配串的串长大于当前最佳匹配串的串长。

显而易见的是：

①在第一种情况下，输出下一个最佳匹配串将是多余的。

②在第二种情况下，输出任何最佳匹配串都不会造成浪费。

③在第三种情况下，输出当前最佳匹配串将是浪费的。

因此，只需要对第三种情况进行判断即可。在获取当前最佳匹配串的同时，获取下一个最佳匹配串，并进行判断。

为此，将此次的字符放入hash表中，并使用下一个字符作为待编码区的起始字符。这样比较此次字符作为待编码区的首字母的匹配长度和下一字符做待编码区首字符的编码长度，这两个长度哪个长就是用哪一个长度保存在压缩的数组之中。

在图2所示的代码中，对两个匹配长度进行比较，得到长度最长的字符串。lgth1是下一字符作为待编码区开头字符时得到的匹配长度，lgth是此次字符作为待编码区开头字符时得到的匹配长度。

1.6 优化Huffman算法

霍夫曼压缩算法的简要步骤如下：

1)统计符号频率：遍历待压缩的数据，统计每个符号(如字符、字节等)出现的频率。

2)构建霍夫曼树：根据符号频率构建一颗霍夫曼树。频率较低的符号作为叶子节点，频率较高的符号位于树的较低层。通过合并最小频率的节点来构建树，直到只剩下一个根节点。

3)分配编码：从根节点开始，沿着树的路径为每个符号分配唯一的二进制编码。一般而言，向左子树走表示编码为0，向右子树走表示编码为1。

4)生成编码数据：遍历原始数据，将每个符号替换为对应的编码，生成压缩后的编码数据。

5)存储压缩数据：将压缩后的编码数据保存到文件或传输给接收方。

6)解压缩时，使用相同的霍夫曼树和编码表，根据编码逐步还原原始数据。

霍夫曼压缩算法通过根据符号频率赋予不同长度的编码，实现了高频符号使用短编码的效果，从而在保证数据完整性的前提下，实现了较高的数据压缩率。它广泛应用于文件压缩、图像压缩、音频压缩等领域。

以下是Huffman压缩编码的一个举例：

假设我们有以下字符串需要进行压缩：“ABBCCCDDDDEEEEE”。

1)统计符号频率：统计每个符号的出现频率。

‘A’：1

‘B’：2

‘C’：3

‘D’：4

‘E’：5

2)构建霍夫曼树：根据符号频率构建霍夫曼树。

从最小频率开始构建树：

①合并频率为1的‘A’和‘B’，得到新节点‘AB’：频率=3

②合并频率为3的‘AB’和‘C’，得到新节点‘ABC’：频率=6

③合并频率为4的‘D’和‘ABC’，得到新节点‘DABC’：频率=10

④合并频率为5的‘E’和‘DABC’，得到新节点‘E(DABC)’：频率=15

得到以下霍夫曼树：

3)分配编码：从根节点开始，沿着左子树走为0，沿着右子树走为1，为每个符号分配编码。

‘A’：编码为：0000

‘B’：编码为：0001

‘C’：编码为：001

‘D’：编码为：01

‘E’：编码为：1

4)生成编码数据：使用编码表，将原始数据替换为对应的编码。

原始数据：“ABBCCCDDDDEEEEE”

替换为编码：“00000001_00010010_01001010_1010 1111_11”

通过霍夫曼压缩算法，原始字符保存下来共需要15个字节，现在只需要5个字节就可以。现在原始字符串被压缩为较短的编码字符串，从而实现了数据的压缩。在解压缩时，使用相同的霍夫曼树和编码表，根据编码逐步还原原始数据。

主要是改进Huffman的存储结构，由于是对某一图像区域进行压缩，因此这个区域的字节数不会太大，对于8*8的tile块，设定的是256字节。如果根据上面的分析可知，压缩和解压缩都需要得到字符出现的概率，以便构建Huffman树和获得Huffman编码。但是由于如果保存一个字符，一个出现的概率，那么如果256个字节中出现了N种字符，那么就需要至少2N的字节保存Huffman字符频率，如果N大于128，那么编码表都比原字符要大了，这样就造成了浪费。于是设置一个标记位，在统计到2N+0.5N>256时，就不在使用Huffman压缩算法，从而保证了压缩速度。同时计算出Huffman文件的大小，如果压缩后的数据大于tile的大小，直接给(*outputsize)赋予一个大于tile的值。

2 压缩算法的FPGA设计

2.1 FPGA平台

该算法实现平台是 Xillinx 的 VivadoHLS2019.1 高级综合工具。接下来主要介绍总体设计结构的实现和优化、功能仿真结果和时序仿真结果。将前几章阐述的算法结构进行实现和优化，通过添加C仿真验证算法的正确性，在此基础上进行硬件电路的实现和优化[17-18]。在 HLS 工具中用到的FPGA是Xilinx的Zynq UltraScale+ MPSoC(多处理器系统级芯片)系列(xczu3cg-sfvc784-1-i)[19-20]。将压缩设计的结构直接通过高级综合工具默认的约束进行综合，得到的时延结果如图3所示。

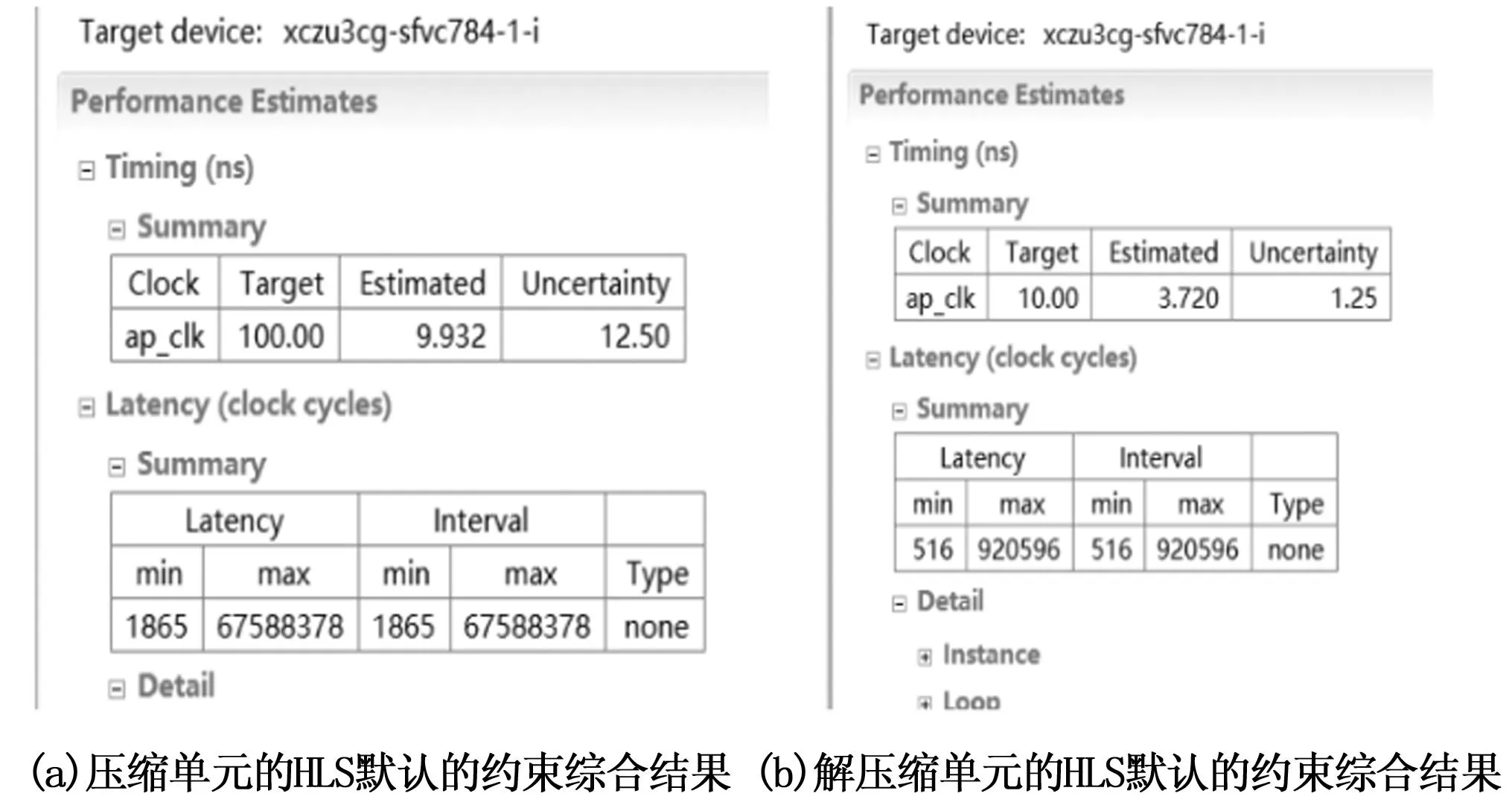
图3 时延结果

2.2 压缩算法的FPGA功能仿真

对VIVADO HLS生成的电路进行功能仿真。设置输入的块数据为：

Unsigned char input[256]={

1,5,1,9,2,0,3,8,3,3,8,4,4,7,8,111,

8,1,4,4,3,8,9,66,74,47,1,3,7,9,5,1,

32,38,47,43,40,1,1,1,1,1,1,2,2,38,1,5,

1,9,2,0,3,8,3,3,8,4,4,7,8,111,1,6,

6,7,8,1,6,9,66,74,47,1,3,7,32,38,47,43,

40,1,1,1,1,1,2,2,3,7,8,100,102,10,15,222,

33,8,65,60,63,44,52,12,14,18,19,1,5,1,9,2,

0,3,8,3,3,8,4,4,7,8,111,1,6,6,7,8,

1,6,9,74,47,1,3,72,7,3,5,9,5,1,32,38,

47,43,40,1,1,1,1,1,1,2,2,3,7,8,1,5,

1,9,2,0,3,8,3,3,8,4,4,7,8,111,1,6,

6,7,8,1,6,9,4,4,3,8,1,3,7,8,2,7,

3,5,9,5,1,32,38,47,43,40,1,1,1,1,1,1,

1,5,1,9,2,0,3,8,3,3,8,4,4,7,8,111,

1,6,6,7,8,1,6,9,4,4,3,8,9,6,78,47,

1,3,7,8,2,7,3,5,9,5,1,32,38,47,43,40}

压缩后的数据为：

nsigned char refer[256]={

20,118,82,1,5,1,9,1,4,251,71,189,25,8,217,1,

255,2,5,0,254,0,41,241,2,99,187,30,207,247,251,3,

4,255,251,46,216,254,42,210,0,6,250,253,4,252,214,0,

253,7,252,5,248,1,7,29,250,7,39,218,29,219,0,37,

227,255,252,107,152,2,248,7,6,3,254,36,230,239,251,2,

1,6,1,255,27,4,3,62,193,4,4,58,193,44,210,7,

50,243,223,246,253,0,149,3,73,189,36,98,122,94,208,245,

66,254,193,2,2,255,8,39,217,4,0,2,0,0,34,64,

32,0,16,36,85,14,194,15,183,180,65,18,210,1,2,11,

2,28,5,14,2,52,3,36,3,11,2,50,5,48,3,28,

5,65,2,93,2,88,5,27,2,36,3,72,3,98,3,85,

6,46,2,50,5,119,2,49,3,61,2,113,6,112,3,93,

2,138,6,179,2,139,3,36,3,72,2,98,4,85,5,11,

2,50,5,49,3,113,6,112,3,104,2,138,6,139,3,0,

0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,

0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0}

首先利用C语言进行仿真，得到的结果是正确的，然后进行FPGA仿真。

压缩电路的功能仿真结果如图4和图5所示。从图4和5可以看出功能仿真完成正确。

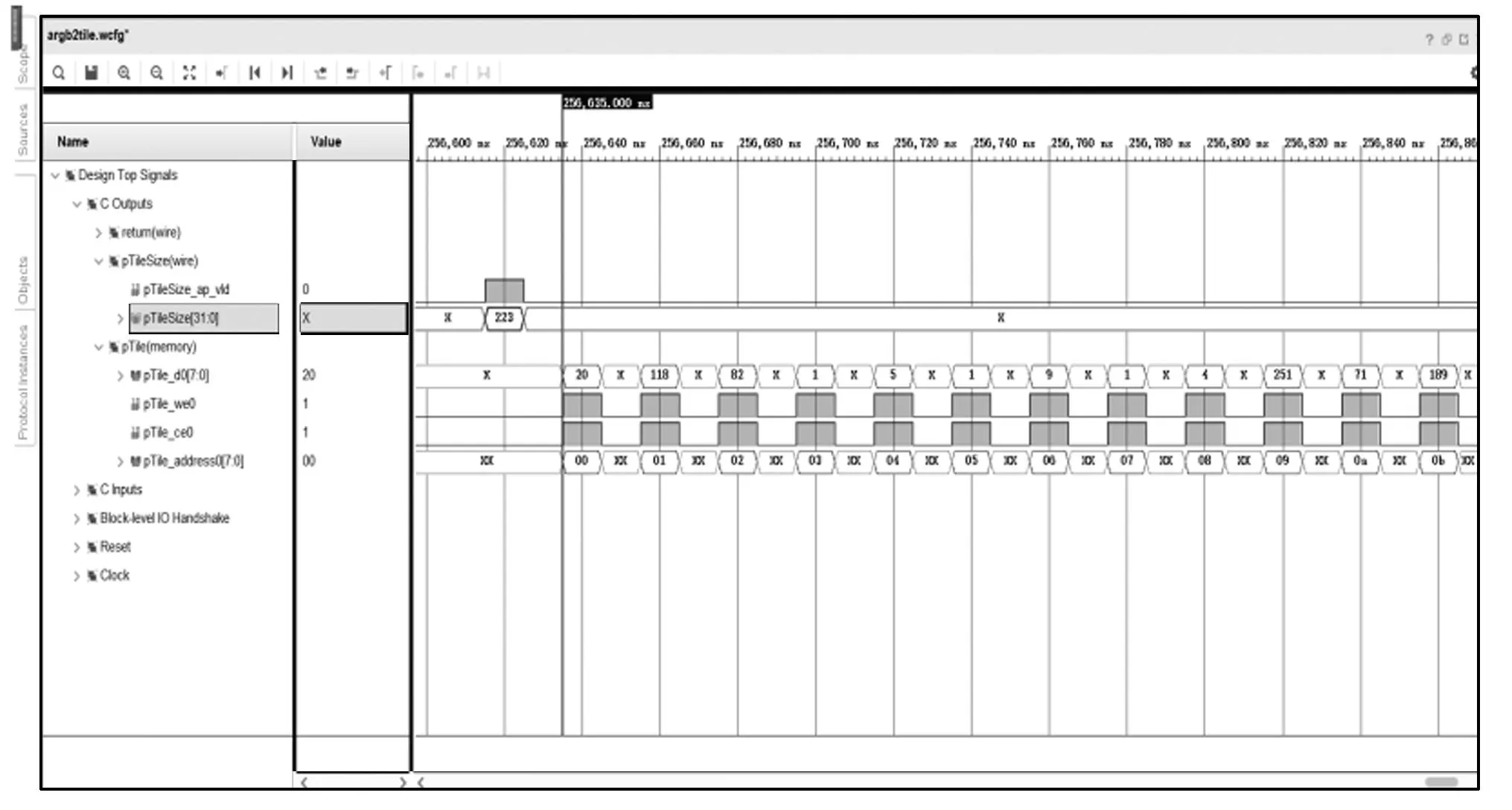
图4 对测试数据1的功能仿真结果

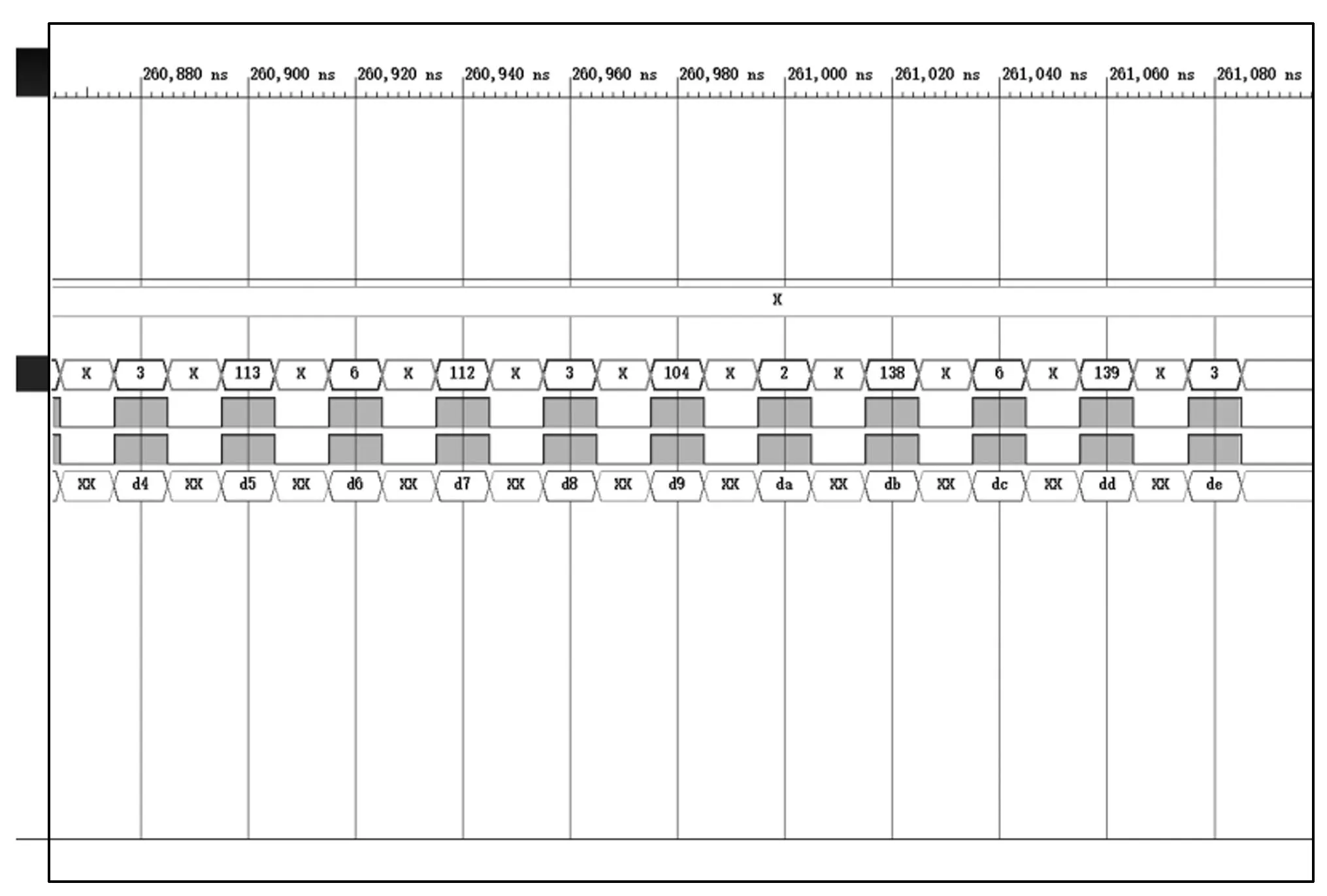
图5 对测试数据1的功能仿真结果

2.3 解压缩算法的FPGA功能仿真

对于C仿真，使用的测试输入数据如下：

Unsigned char input[256]={

20,118,82,1,5,1,9,1,4,251,71,189,25,8,217,1,

255,2,5,0,254,0,41,241,2,99,187,30,207,247,251,3,

4,255,251,46,216,254,42,210,0,6,250,253,4,252,214,0,

253,7,252,5,248,1,7,29,250,7,39,218,29,219,0,37,

227,255,252,107,152,2,248,7,6,3,254,36,230,239,251,2,

1,6,1,255,27,4,3,62,193,4,4,58,193,44,210,7,

50,243,223,246,253,0,149,3,73,189,36,98,122,94,208,245,

66,254,193,2,2,255,8,39,217,4,0,2,0,0,34,64,

32,0,16,36,85,14,194,15,183,180,65,18,210,1,2,11,

2,28,5,14,2,52,3,36,3,11,2,50,5,48,3,28,

5,65,2,93,2,88,5,27,2,36,3,72,3,98,3,85,

6,46,2,50,5,119,2,49,3,61,2,113,6,112,3,93,

2,138,6,179,2,139,3,36,3,72,2,98,4,85,5,11,

2,50,5,49,3,113,6,112,3,104,2,138,6,139,3}

解压后的数据如下：

Unsigned char refer[256]={

1,5,1,9,2,0,3,8,3,3,8,4,4,7,8,111,

8,1,4,4,3,8,9,66,74,47,1,3,7,9,5,1,

32,38,47,43,40,1,1,1,1,1,1,2,2,38,1,5,

1,9,2,0,3,8,3,3,8,4,4,7,8,111,1,6,

6,7,8,1,6,9,66,74,47,1,3,7,32,38,47,43,

40,1,1,1,1,1,2 ,2,3,7,8,100,102,10,15,222,

33,8,65,60,63,44,52,12,14,18,19,1,5,1,9,2,

0,3,8,3,3,8,4,4,7,8,111,1,6,6,7,8,

1,6,9,74,47,1,3,72,7,3,5,9,5,1,32,38,

47,43,40,1,1,1,1,1,1,2,2,3,7,8,1,5,

1,9,2,0,3,8,3,3,8,4,4,7,8,111,1,6,

6,7,8,1,6,9,4,4,3,8,1,3,7,8,2,7,

3,5,9,5,1,32,38,47,43,40,1,1,1,1,1,1,

1,5,1,9,2,0,3,8,3,3,8,4,4,7,8,111,

1,6,6,7,8,1,6,9,4,4,3,8,9,66,78,47,

1,3,7,8,2,7,3,5,9,5,1,32,38,47,43,40}

解压电路的功能仿真如图6和图7所示。

图6 解压单元对测试数据1的功能仿真结果

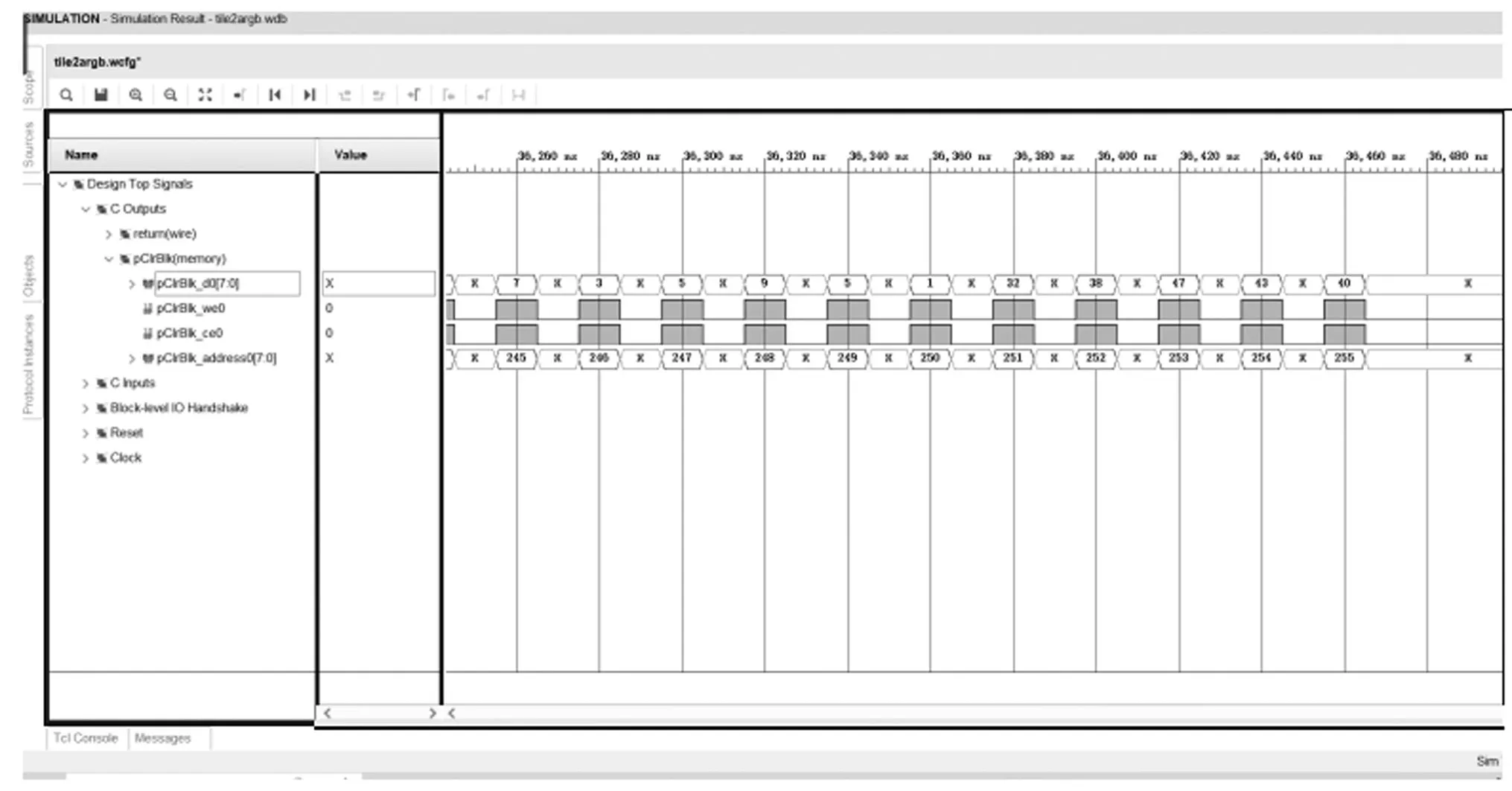
图7 解压单元对测试数据1的功能仿真结果

2.4 时序仿真结果

HLS导出RTL代码后进行了时序仿真，在这里设置的时钟频率是100 MHz。

由图8可以看出，最坏路径的建立时间裕量为2.679 ns，那么可以估计出单元的最高时钟频率约为136 MHz。

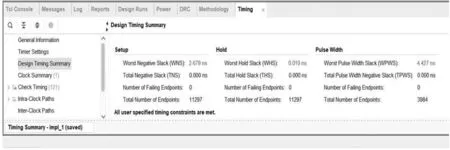
图8 压缩单元的时序仿真结果

同理对于解压缩单元，最坏路径的建立时间裕量为6.264 ns，同样也可以估计出解压缩单元的最高时钟频率约为267 MHz。

3 测试结果

使用了33张测试图片，在Linux系统下对本算法进行了测试，测试的图片和压缩率如表1所示。

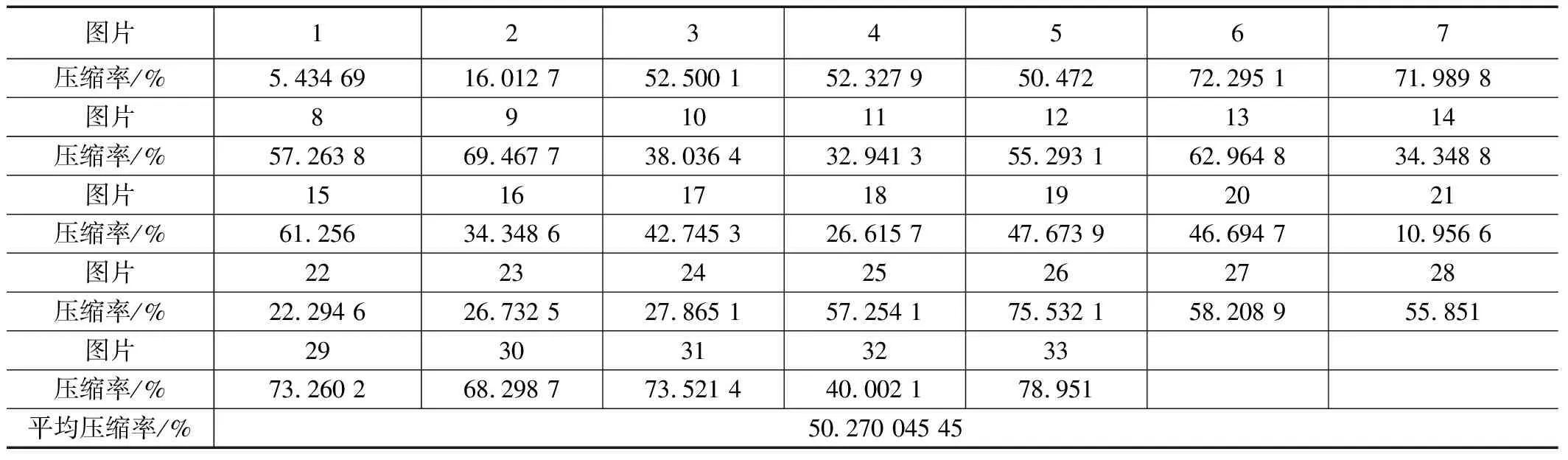
表1 图片和压缩率表

在Linux系统下对Deflate算法进行了测试，测试的图片和压缩率如表2所示。

表2 图片和压缩率表

接下来对该算法与Deflate算法进行相应的比较。基于进行的图片压缩测试结果，本算法在处理那些具有丰富细节的图片时，其压缩性能表现相对较差。然而，当处理那些相对平坦且细节不太丰富的图片时，该算法展现出了较为出色的压缩效果。而对于Deflate算法来说，其压缩率相对集中，对细节丰富的图片压缩得较好，然而平均压缩率不如该算法。

4 结束语

使用C语言实现了一种针对图像的区域压缩算法，并采用Huffman算法和LZ77算法分别对压缩区域进行压缩。通过选择较小的压缩文件来实现更高的压缩率。为了验证算法的功能可实现性使用VIVADO HLS工具进行功能仿真验证算法在不同压缩区域大小下的压缩和解压功能性，从而确保算法在硬件实现中的功能正确性，为图像压缩领域的进一步研究和应用提供了有力支持。