Improved decoy-state quantum key distribution with uncharacterized heralded single-photon sources
2024-02-29LeChenXu徐乐辰ChunHuiZhang张春辉XingYuZhou周星宇andQinWang王琴
Le-Chen Xu(徐乐辰), Chun-Hui Zhang(张春辉), Xing-Yu Zhou(周星宇), and Qin Wang(王琴),†
1Institute of Quantum Information and Technology,Nanjing 210003,China
2Broadband Wireless Communication and Sensor Network Technology,Key Laboratory of Ministry of Education,Nanjing University of Posts and Telecommunications,Nanjing 210003,China
3Telecommunication and Networks National Engineering Research Center,Nanjing University of Posts and Telecommunications,Nanjing 210003,China
Keywords: quantum key distribution,heralded single-photon source,decoy-state method
1.Introduction
Quantum key distribution (QKD),[1,2]based on the fundamental laws of physics,[3,4]allows two distant parties,Alice and Bob, to share secret keys in the presence of a malicious eavesdropper,Eve.Since the first QKD protocol(BB84)was proposed in 1984,[1]a great number of QKD experiments have been reported.[5–12]In most previous QKD protocols and corresponding security proofs,[13–19]people often assume the prepared states are perfect.However,preparation flaws inevitably exist in real-life situations due to the imperfect devices,resulting in reduced security of practical QKD systems.
To alleviate the influence of state preparations flaws,Tamakiet al.[20]presented a loss-tolerant protocol, but it requires full characterization of the preparation states and causes increased system complexity.Fortunately, Yinet al.[21]proposed a QKD protocol without characterizing misalignment errors and the only assumption is that the quantum states are prepared in a two-dimensional Hilbert space.With which the secret keys can be extracted out using uncharacterized sources by exploiting the mismatched-basis statistics which are normally discarded, and related experiments have been successfully demonstrated.[22–24]
Based on those previous works,[21–23]here we present a four-intensity decoy-state proposal on quantum key distribution using uncharacterized heralded single-photon sources(HSPS).First,the four-intensity scheme with biased basis can help to improve the key rate compared with the standard threeintensity method.[22,23]Second,by employing the intrinsic advantages of HSPS with a higher single-photon probability and a lower dark count rate compared with weak coherent sources(WCS),[25,26]one can obtain not only a much longer secure transmission distance, but also a higher key rate, compared with previous similar works.[22,23]
2.Protocol description
In our four-intensity BB84 protocol, Alice randomly modulates each pulse into one of the four different intensities,i.e.,the signal stateµ,the decoy statesνandω,and the vacuum stateo.However, different from the standard threeintensity method,Alice only prepares the signal pulses in basisZAand randomly prepares the decoy pulses in basisZAor basisXA.Considering typical encoding misalignments, Alice randomly prepares quantum states|ϕ0〉=|0〉,|ϕ1〉=sina|0〉+cosa|1〉,|ϕ2〉 = cos(π/4+b)|0〉+sin(π/4+b)|1〉,|ϕ3〉 =sin(π/4+c)|0〉-cos(π/4+c)|1〉, in which the degrees of anglesa,b, andcare the encoding misalignments.We define that basisZAconsists of|ϕ0〉 and|ϕ1〉, while basisXAconsists of|ϕ2〉 and|ϕ3〉.Besides, we make the assumption that Bob performs projective measurement on the received states to ensure protocol security.[21]Let Bob’s measurement for basisZBbe a projection onto{|¯ϕ0〉,|¯ϕ1〉}, and for basisXBbe{|¯ϕ2〉,|¯ϕ3〉}, where〈¯ϕ0|¯ϕ1〉 =〈¯ϕ2|¯ϕ3〉 = 0 and|¯ϕ0〉〈¯ϕ0|+|¯ϕ1〉〈¯ϕ1| =|¯ϕ2〉〈¯ϕ2|+|¯ϕ3〉〈¯ϕ3| =I.After basis sifting, the number of detected pulses can be obtained,of which matched-basis events are kept as sifted keys and mismatched-basis events are used to estimate the information leaked to Eve.
By sacrificing some bits from matched-basis events and revealing all bits from mismatched-basis events, we can deduce conditional probability distributionPλ(y|x),whereλ ∈{µ,ν,ω,o},x ∈{|ϕ0〉,|ϕ1〉,|ϕ2〉,|ϕ3〉}andy ∈{|¯ϕ0〉,|¯ϕ1〉,|¯ϕ2〉,|¯ϕ3〉}.For simplicity, we assign value 0 to|ϕ0〉 and|¯ϕ0〉, value 1 to|ϕ1〉 and|¯ϕ1〉, value 2 to|ϕ2〉 and|¯ϕ2〉, and value 3 to|ϕ3〉 and|¯ϕ3〉.Pλ(y|x) can be expressed as follows:
ηt=η10-αl/10represents the total transmission and detection efficiency,whereηrepresents the detection efficiency of the single-photon detector,αdenotes the loss coefficient of standard optical fibers andLdenotes the fiber length.F(j)represents the probability of the valid detection events (those only one detector clicks)onj-photon states,such as
wheredrepresents the dark count rate of the single-photon detector andPi(λ)is the photon number distribution of the light sources.Here, we take HSPS as the uncharacterized source.Through a parametric down-conversion process, a two-mode state,including the idler mode and the signal mode,[27]is generated in HSPS.The idler modes are detected by Alice’s local single-photon detector working as heralding signals and the signal modes will be encoded and sent out to Bob.The photon number distribution of HSPS can be expressed as[26]
wheredAandηAeach denote the dark count rate and the detection efficiency of Alice’s local detector,respectively.
With Eqs.(1)–(3), we can obtain the expression of each observableMλ(y|x),namely the number of valid detections at Bob’s side after sifting.Considering statistical fluctuation,we use method in Refs.[28,29] to account for the finite-size key effects, which provides a tighter bound for the deviation between ideal expectations and actual observations.Then, the underlying expectation value ofMλ(y|x) for a given failure probabilityεis

whereNλ(y|x) represents the total conditional detection events.Then,by using decoy-state method,[5,25]we can bound the conditional probabilities of single-photon eventsp(y|x)for both matched-basis and mismatched-basis as
Thus, the detections on single-photon pulses with intensityλin basisZcan be expressed as
and the lower bound of theMZ1,λsatisfies the following expressions:
where

and the single-photon phase error rate is bounded by



We note thatp(y|x) in the above equations is constrained by lower boundp(y|x)Land upper boundp(y|x)U.
Finally,the secret key rate in basisZis given by[23]

3.Numerical simulation and discussion
In this section, we carry out corresponding numerical simulations for our present scheme.In order to show the performance of our scheme, we first compare it with the threeintensity method in Ref.[23].To explain the main factors that make our scheme performs better, we do comparison of the phase error rate and comparison of the numbers of valid single-photon detection events used to generate final key bits.Indispensably, we also show that our scheme can generate secret key against encoding misalignments.Moreover,we also do comparisons between using HSPS and WCS.The full parameter optimization is carried out to obtain better performance, including optimizing the intensities of the signal state,two decoy states,and the probability to prepare quantum states with different intensities.In practical implementation of QKD,people often use the non-degenerated parametric downconversion to produce photon pairs, with one photon at the wavelength convenient for detection acting as heralding signal, and the other falls into the telecommunication windows for optimal propagation along the fiber or in open air acting as heralded signal.For example, in Ref.[10], the idler mode and signal mode are each centered at 633 nm and 1545 nm,respectively,and each is detected with a silicon-avalanche photodiode detector (SAPD) and InGaAs single-photon detector.Therefore, in our simulations, we have set reasonable values for the system parameters as shown in Table 1.Simulation results are shown in Figs.1–5.

Table 1.List of practical parameters for simulations. η(ηA)represents the detection efficiency of the single-photon detector at Bob(Alice)’s side;d (dA)represents the dark count rate of the singlephoton detector at Bob (Alice)’s side; ed is the misalignment-error probability; α denotes the loss coefficient of standard optical fibers; fEC represents the inefficiency of error correction;ε represents the failure probability and N represents the total number of pulses sent out by Alice.
In Fig.1,we do comparisons on the key rate between using different light sources(HSPS and WCS)and using different decoy-state methods whena=b=c=0◦,i.e.,the threeintensity method[23]and the present four-intensity method.When comparing with using different light sources, it shows that HSPS experiences an enhancement of 17 km in the transmission distance,approximately 14%improvement due to the much lower vacuum component in HSPS.On the other hand,when comparing schemes with different decoy-state methods,although there is no obvious improvement in transmission distance,the four-intensity scheme significantly increases the key rate.As a result, the combination of HSPS and the fourintensity scheme can improve both the secure key rate and the transmission distance.
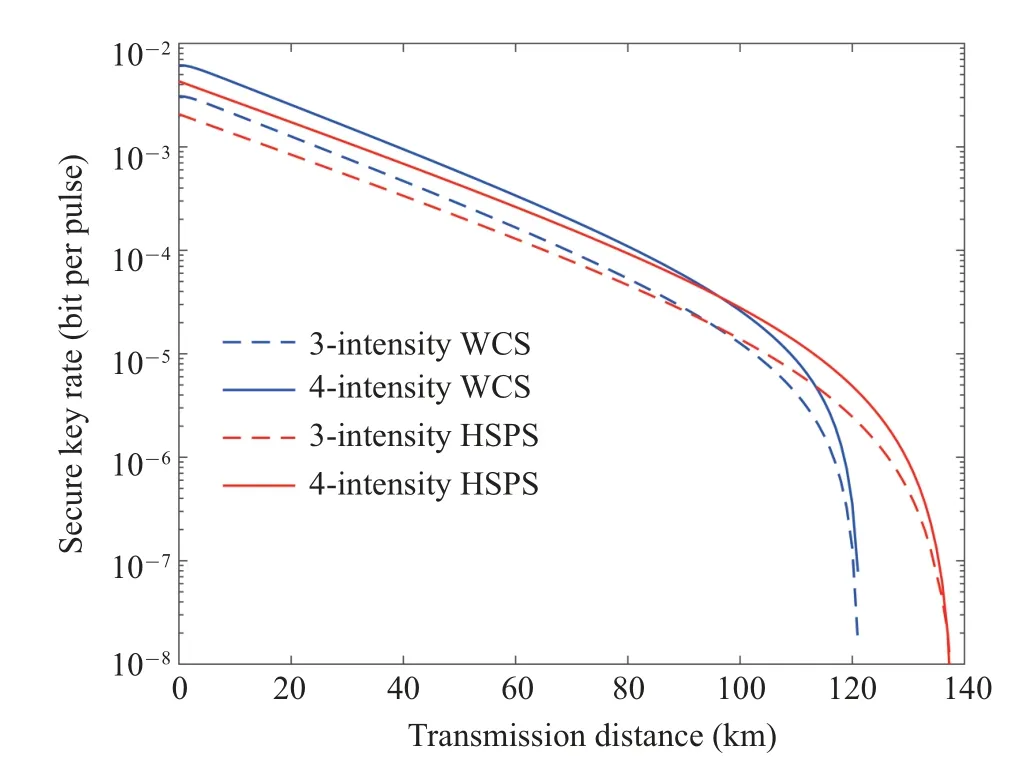
Fig.1.Secure key rate versus transmission distance for different decoy-state schemes: The red solid(dash)lines represent four(three)-intensity method with HSPS for a=b=c=0◦.The blue solid (dash) lines represent four(three)-intensity method with WCS for a=b=c=0◦.
We compare the phase error rate and the single-photon detection event between using different light sources whena=b=c=0◦in Figs.2 and 3 respectively.As we can see from Fig.2 that, our present work using HSPS gives a much lower phase error rate comparing those using WCS because of the negligible vacuum components.Besides, for the ones using WCS, the curves of the single-photon detection event decline rapidly after 120 km,while for those using HSPS,the cut-off points reach up to 140 km.
In Fig.4,based on four-intensity decoy-state method with HSPS(WCS),we plot out variations of the key rate with transmission distance under different values of encoding misalignments.The transmission distance decreases 4 km(5 km)whena=b=c= 3◦and 18 km (23 km) whena=b=c= 6◦as using HSPS (WCS).Overall, our protocol exhibits excellent tolerance to the existence of misalignment errors.It is worth noting that there is no need to characterize encoding errors in practical applications for our scheme,and consequently above-mentioned misalignments are just used to test the robust.
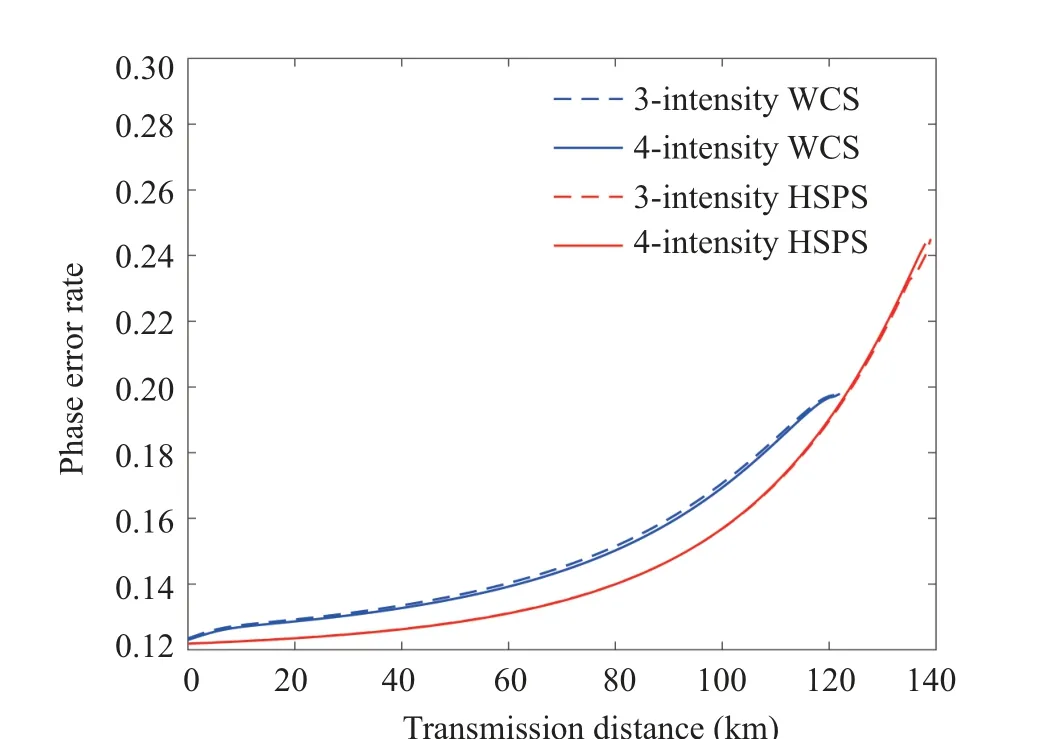
Fig.2.Phase error rate versus transmission distance for different decoystate schemes.The red solid (dash) lines represent four (three)-intensity method with HSPS for a=b=c=0◦.The blue solid(dash)lines represent four(three)-intensity method with WCS for a=b=c=0◦.
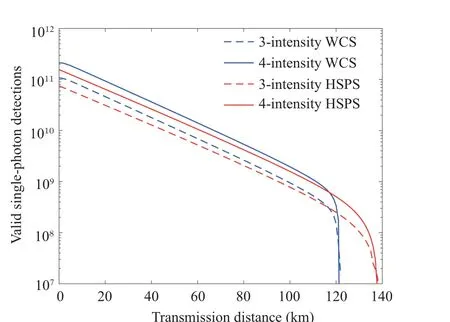
Fig.3.Valid single-photon detections versus transmission distance for different decoy-state schemes.The red solid(dash)lines represent four(three)-intensity method with HSPS for a=b=c=0◦.The blue solid(dash)lines represent four(three)-intensity method with WCS for a=b=c=0◦.

Fig.4.Secure key rate versus transmission distance for different schemes with different source preparation errors.The red lines represent fourintensity method with HSPS for a=b=c=0◦, 3◦, 6◦.The blue lines represent four-intensity method with WCS for a=b=c=0◦,3◦,6◦.
Finally, we do investigation on the detection efficiency of the local detectors at Alice’s side (ηA), by fixing the encoding misalignments asa=b=c=3◦, see Fig.5.We can see from Fig.5 that the higher the detection efficiency, the higher the key rate and the transmission distance.With the state-of-the-art superconducting nanowire single-photon detector(ηA=0.9),[30]our scheme only presents a slightly lower key rate than the one using WCS at short transmission distance(<90 km);while shows more than 20-km longer transmission distance.

Fig.5.Secure key rate versus transmission distance by using different light sources: The blue lines represent four-intensity method with WCS.The red lines represent four-intensity method with HSPS for ηA=0.9 and 1.
4.Conclusion
In conclusion, we have presented an improved decoystate QKD protocol with uncharacterized HSPS and investigated its performance.By exploiting the mismatched-basis statistics and preparing quantum states in a two-dimensional Hilbert space,our scheme reduces the requirements for preparation errors and lowers the system complexity compared with normal BB84 QKD protocol.Moreover,our simulation results show that the secure key rate and transmission distance have been significantly improved by using our present scheme comparing with former similar protocols.Therefore, our present work seems to be a very promising choice for practical implementations of QKD systems.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant Nos.12074194, 12104240, and 62101285), the Industrial Prospect and Key Core Technology Projects of Jiangsu Provincial Key Research and Development Program (Grant No.BE2022071), and the Natural Science Foundation of Jiangsu Province, China (Grant Nos.BK20192001 and BK20210582).
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Quantum synchronization with correlated baths
- Preparing highly entangled states of nanodiamond rotation and NV center spin
- Epidemic threshold influenced by non-pharmaceutical interventions in residential university environments
- Dynamical behavior of memristor-coupled heterogeneous discrete neural networks with synaptic crosstalk
- Dynamics and synchronization in a memristor-coupled discrete heterogeneous neuron network considering noise
- Spatial search weighting information contained in cell velocity distribution
