Dynamics and synchronization in a memristor-coupled discrete heterogeneous neuron network considering noise
2024-02-29XunYan晏询ZhijunLi李志军andChunlaiLi李春来
Xun Yan(晏询), Zhijun Li(李志军),†, and Chunlai Li(李春来)
1School of Automation and Electronic Information,Xiangtan University,Xiangtan 411105,China
2School of Computer Science&School of Cyberspace Science,Xiangtan University,Xiangtan 411105,China
Keywords: heterogeneous neuron network,discrete memristor,coexisting attractors,synchronization,noise
1.Introduction
Studying neuromorphic behaviors of neurons is favorable to help us to understand more about the operating mechanism of the brain.Therefore, establishing appropriate neuron models to simulate the dynamic behavior of biological neurons has received widespread attention.[1–3]The Hodgkin–Huxley (HH) model was the first established neuron paradigm,[4]which demonstrates the connection between the membrane voltage of neurons and the membrane currents of squid giant axons.However, the HH model is formulated by seven coupled ordinary differential equations and includes four ionic channels,which lead to its complexity.Some simplified models, thus, have been proposed to simulate the neuromorphic behaviors of the biological neurons, such as FitzHugh–Nagumo(FHN)model,[5–8]Hindmarsh–Rose(HR)model,[9–13]Morris–Lecar(ML),[14–18]etc.These continuous neuron models have played an important role in understanding the generation and transmission of action potential.[19–23]
Compared with continuous neuron models,discrete neuron models are more computationally efficient, especially in the modeling of large-scale neuron networks.The modeling of discrete neurons and the analysis of their firing patterns have become a hot topic in the field of neurodynamics in recent years.[24–27]Due to the non-volatile, nanoscale,memory properties of memristors,and the similarity between nano-scale moving particles in memristors and mobile neurotransmitters in biological synapses, memristors are often considered as ideal candidates for simulating synapses.[28–32]For example, Baoet al.[33]established a discrete neuron network containing two identical Rulkov neurons, and regarded the current flowing through the memristor as the electromagnetic induction current to analyze the effect of electromagnetic induction on the dynamic behavior of neuron network.Under the influence of the electromagnetic induction current,the model can achieve complete synchronization and lag synchronization.The synchronous firing and chimera state were observed in a ring neuron network constructed with memristorcoupled discrete Chialvo neurons.[34]Mahtab Mehrabbeiket al.[35]studied the memristive Rulkov neuron maps and analyzed the synchronous dynamics under electrical and chemical coupling.Their results shows that two m-Rulkov neurons can achieve synchronization only when electrically coupled,but not when chemically coupled.Liet al.[36]used discrete locally active memristor to construct a logarithmic map, and the coexisting attractors were observed.
Among many neuron models, the Izhikevich model simplifies the HH model[37–40]with consideration of biological concepts, which is capable of simulating almost all spikes of cortical neurons.[41,42]Furthermore, the Izhikevich model outperforms other models in terms of computational efficiency.[43–46]The Chialvo model is one of the earliest discrete neuron models,[47,48]and it was attempted to study the synchronous rhythmic activity in some areas of mammals at that time,[48]including the cortical spindle rhythms, hyppocampal rhythms, and somatomotor cortices.The Chialvo model can demonstrate key patterns of neuronal activities,such as spiking,excitations,bursting,and so on.
In fact, the brain is a very complex system, which can be divided into many brain regions,including the motor area,sensory area, visual area, auditory area and association area,just to name a few.[49]The neurons in different brain regions are independent but interact with each other, and jointly control neural activities of the human body.[50,51]Therefore,neuron networks composed of heterogeneous neurons is more in line with biological reality.However, to our knowledge, previous studies on discrete neuron networks mainly focus on homogeneous neurons,while neuron networks composed of heterogeneous neurons coupled by memristors are rarely studied.To further understand the operating mechanism of the brain,it is essential and meaningful to study the dynamic behavior of neuron networks constructed with heterogeneous neurons distributed in different brain regions.[52–54]In addition,in the biological nervous systems, a large number of neurons work together,which inevitably leads to changes in the surrounding physiological environment.Therefore, noise is ubiquitous in the biological nervous systems.[44]However,it is currently unclear how noise affects the information processing mechanism of neurons, so the impact of noise on the firing activities of neurons cannot be ignored.[55–57]
In the present study,we propose a new discrete locally active memristor and use it to connect the discretized Izhikevich and Chialvo neurons.Thus, a heterogeneous discrete neuron network model coupled by the discrete locally active memristor is constructed.The dynamics of the neuron network are analyzed, and the synchronous behavior between two heterogeneous neurons are revealed.Finally,Gaussian noise is added to the model to analyze the impact of noise on firing activities of neuron network.
The rest of this paper is organized as follows.Section 2 proposes a new four-stable locally active discrete memristor and studies its properties in detail.In Section 3, a heterogeneous discrete neuron network model is developed by using the discrete memristor to bridge two heterogeneous neurons and the equilibrium points of the model and their corresponding stabilities are theoretically analyzed.The dynamic behavior and coexistence behavior of neuron networks are revealed in Section 4.Section 5 studies the effect of adding noise on the phase synchronization of neuron networks.Finally,the study is concluded in Section 6.
2.Four-stable locally-active memristor model and characteristics
2.1.Memristor model
The discrete memristor proposed in this paper can be described as follows:
wherev,i,andw(φ)are the input voltage,output current,and admittance function,respectively.F(φ,v)is the internal state equation of the memristor, which consists of a sign function related to the magnetic flux and voltage, andα,β,λare the three parameters of the memristor.In this paper,α= 0.1,β=0.001,andλ=9.
2.2.Pinched hysteresis loops
A periodic voltage signalv(n)=Asin(2πωT(n)) is applied to the memristor, and the initial value of the memristor is selected as 1.By varying the amplitudeAand frequencyω, the memristor shows pinched hysteresis loops on thev–iplane,as shown in Fig.1.
It can be seen from Fig.1 that all the pinched hysteresis loops pass through the origin.When the frequencyω=0.0001 is fixed,the area of the pinched hysteresis loop lobe increases monotonously as the excitation amplitudeAincreases.Once the amplitudeA=20 is fixed,the pinched hysteresis loop lobe area decreases monotonously with the increase of excitation frequencyω.Thus,the proposed memristor satisfies the three characteristic fingerprints of a generalized memristor.[58]
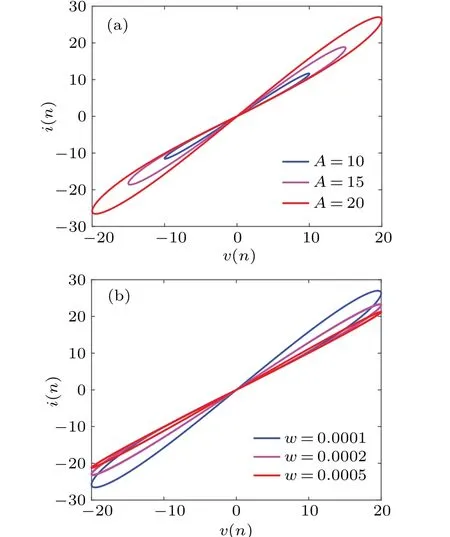
Fig.1.Pinched hysteresis loops of locally active discrete memristor.(a) Amplitude-dependent pinched hysteresis loops with A = 10, 15,and 20.(b)Frequency-dependent pinched hysteresis with ω =0.0001,0.0002,and 0.0005.
2.3.Nonvolatility and local activity
Non-volatility means that a memristor can maintain its latest memductance value when the power is off, which can be verified by the power off plot (POP).If there are multiple negative slope intersections between the POP and the zero horizontal axis,then the memristor is non-volatile.Letvn=0 in Eq.(1),the resulting POP is shown in Fig.2.
From Fig.2, it is observed that there are seven intersection points where the POP intersects theϕaxis, namely,Q1(-1,0),Q2(0,0),Q3(1,0),Q4(2,0),Q5(3,0),Q6(4,0), andQ7(5,0), among which the intersections with a negative slope are the stable equilibrium points, and the other intersections are unstable points.Therefore, the proposed memristor has four stable equilibrium pointsQ1,Q3,Q5, andQ7.When the power is off, the stateϕwill trend to one of the four stable equilibrium points,depending on the attractive domain in which the fnial stateϕ(n) is located.Based on Eq.(1), four possible remembered memductances after power-off are obtained as
implying that the memristor is non-volatile.
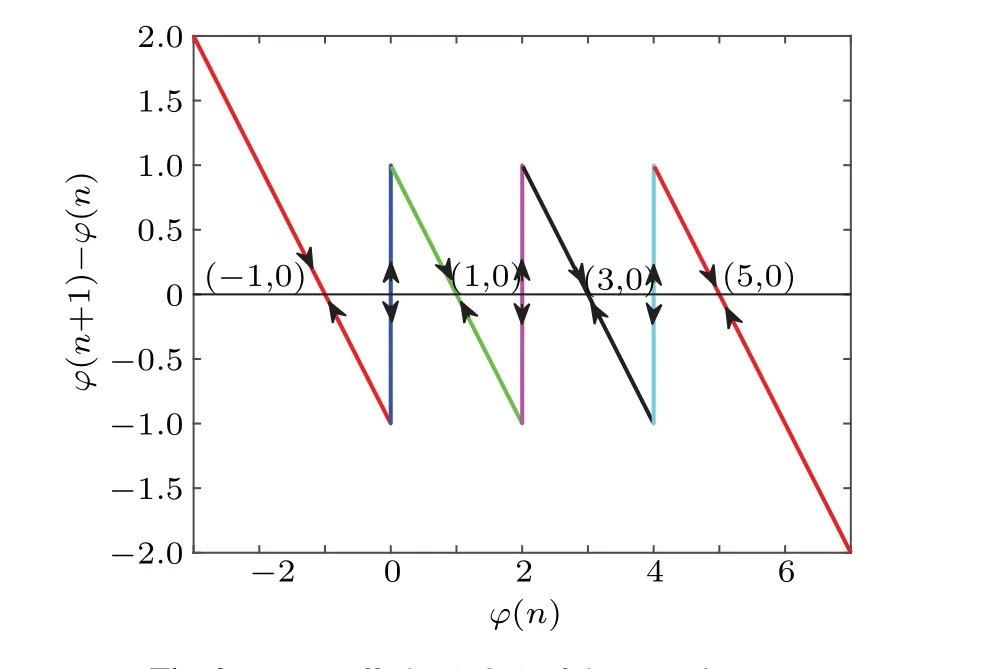
Fig.2.Power-off plot(POP)of the memristor.
In circuit theory, the DCV–Idiagram is a visual tool to help us analyze whether the memristor is locally active.The region with a negative slope in the DCV–Idiagram is called the locally active region of the memristor.Letϕ(n+1)-ϕ(n)=0, we can get the following expressions of voltageVand currentI:
Imposing a voltage in the range-2 V≤V ≤1 V on the memristor, the corresponding DCV–Icurve can be obtained according to Eq.(3),as shown in Fig.3(a).The negative slope regions can be observed in the DCV–Idiagram,which are locally active regions of the memristor.In addition,the pinched hysteresis loops of this local active memristor under different initial values are shown in Fig.3(b).

Fig.3.(a)The DC V–I diagram of the four-stable locally active discrete memristor.(b)The coexisting hysteresis loops with different initial values.
3.Discrete heterogeneous neuron network
3.1.Memristor coupled discrete heterogeneous neuron network
For the discretization of the original Izhikevich neuron,the improved discrete Izhikevich neuron model is written as

wherevanduare the neuron membrane potential and membrane recovery variables respectively,Iis the external excited current and the parametersa,b,c,anddare all dimensionless parameters.This improved Izhikevich model is more computationally efficient, and thus iterative calculations can be performed at a very fast rate.
The discrete Chialvo model is written as
wherexis the membrane potential of the neuron,yis the recovery variable,Itsimulates the effect of the ionic current injected into the neuron, the parameterarepresents the recovery time(a<1), the activation dependence of the recovery process is defined byb(b<1),and the constantcrepresents the offset,which can balance the firing states of the model.
Based on the discrete Izhikevich model and the discrete Chialvo model,a new neuron network model based on locally active discrete memristor is constructed as follows:
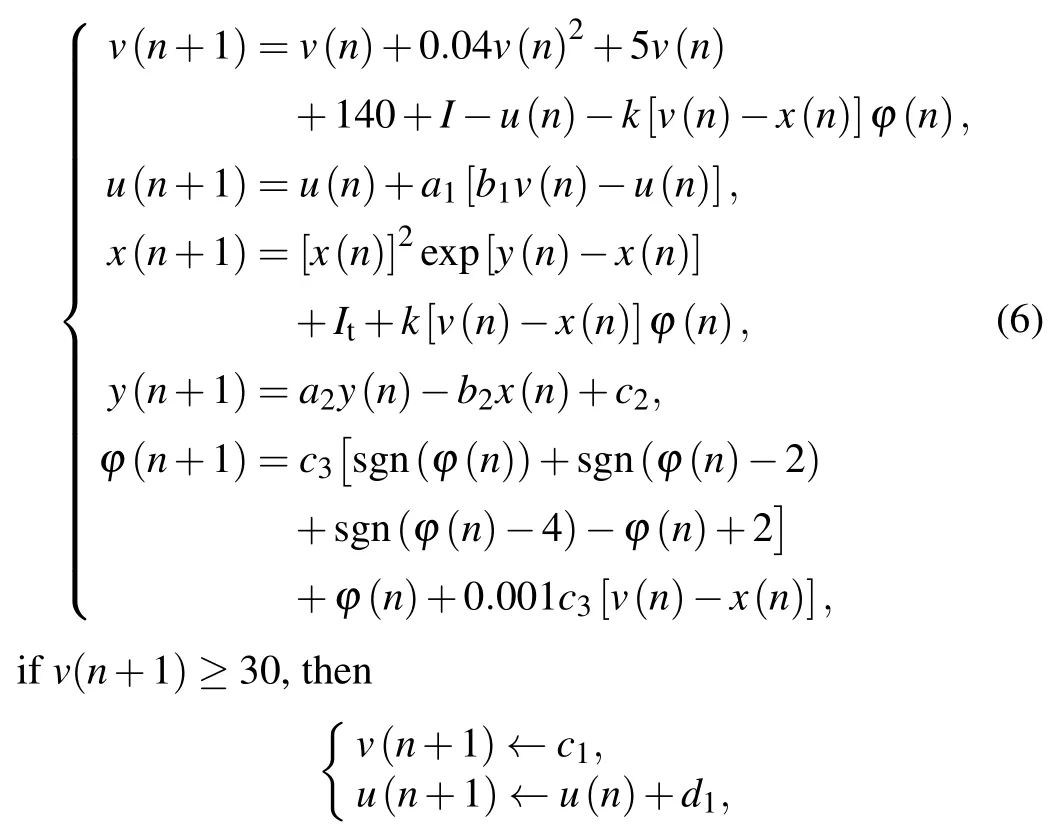
wherekis the coupling strength,and the parameters areI=1,a1=0.02,b1=0.25,c1=-55,d1=2,a2=0.9,b2=0.18,c2=0.28,It=0.03,c3=0.1.For an intuitive understanding of the proposed discrete heterogeneous neuron network,its topology is shown in Fig.4.
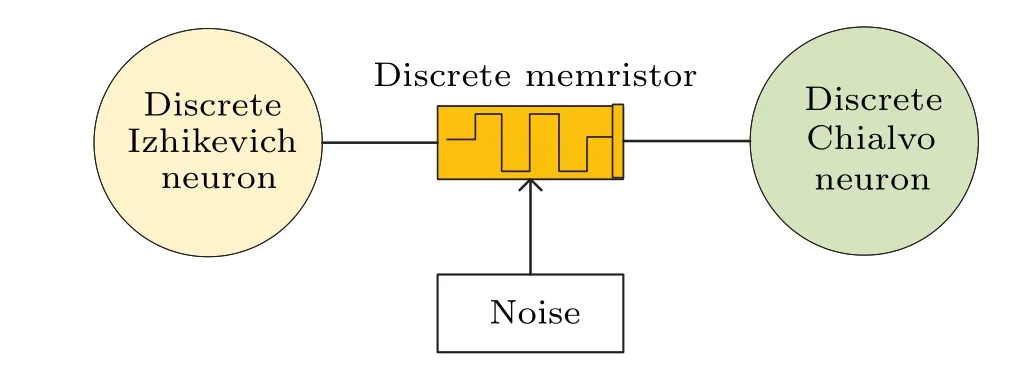
Fig.4.The topology of the new discrete heterogeneous neuron network.
and the relationship betweenvandxsatisfies the following expression:
Therefore, two equations containing onlyxandϕcan be obtained.Note that the signum function is approximated by a hyperbolic tangent function with a large slope, namely,tan(1010ϕ)is used instead of sign(ϕ).The Jacobian matrix at each equilibrium pointE(v,0.25v,x,-1.8x+2.8,ϕ) is given below:
where
3.2.Stability analysis of equilibrium points
Stability analysis plays an important role in studying the firing behavior of neurons.From Eq.(6),the equilibrium point setEis described as


Fig.5.Two function curves and their intersection points.
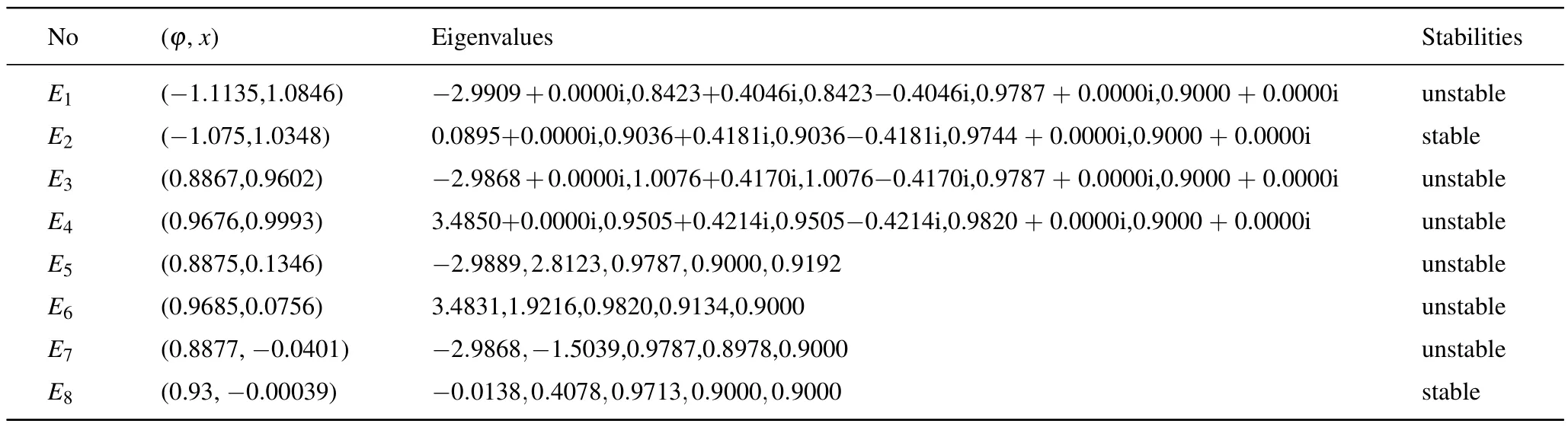
Table 1.The eigenvalues and stability with k=0.001.
Takingk=0.001, figure 5 shows the curves of Eq.(8)in the interval[-2,2].In order to examine whether the equilibrium pointsE1,E2,E3,E4,E5,E6,E7, andE8are stable,the eigenvalues corresponding to these equilibrium points are obtained as shown in Table 1.Based on the stability theory of discrete systems, a equilibrium point is stable when its all eigenvalues are located inside the unit circle, while it is unstable when one of the eigenvalues is located outside the unit circle.It can be seen from Table 1 that the equilibrium pointsE2, andE8are stable, while the other equilibrium points are unstable.
4.Dynamics of heterogeneous discrete neuron networks
In this section, we will study the dynamic behavior of the coupled neuron network under different initial values of the memristor and the coupling strengthk.The other parameters are determined asI=1,a1=0.02,b1=0.25,c1=-55,d1=2,a2=0.9,b2=0.18,c2=0.28,It=0.03,andc3=0.1.The MATLAB iterative algorithm is used in the following calculation.
4.1.Coupling strength dependent dynamics
Bifurcation diagram and Lyapunov exponents are common methods for analyzing system dynamics.In this study,we use the quadrature rectangle (QR) decomposition method to calculate the Lyapunov exponents.Consideringkas the bifurcation parameter with the step size 0.001 and selecting the initial value of the network (-6,-1, 1, 1, 1) as an example, the bifurcation diagram and Lyapunov exponents are shown in Figs.6(a)and 6(b),respectively.It can be seen from Fig.6(a)that the system initially exhibits chaotic firing whenkis located at the interval[-0.54,-0.453], where the corresponding maximum Lyapunov exponentLE1is greater than zero,as observed in Fig.6(b).Then,a reverse period-doubling bifurcation route occurs fork ∈[-0.452,0.0018],resulting in the appearance of periodic spiking.As illustrated in Fig.6(b),all Lyapunov exponents are less than zero in this parameter interval,verifying that the neuron network is in a periodic state.Whenkincreases to the critical valuek=0.0018, a tangent bifurcation occurs,resulting in the occurrence of hyperchaotic firing, which can be validated from the superimposed local magnification plot in Fig.6(b),where the Lyapunov exponentsLE1andLE2are both greater than zero.The sampled phase diagrams and the corresponding time series withk=-0.46,k=-0.4,andk=0.065 are shown in Fig.7,which effectively validate the three parameter regions of chaotic, periodic, and hyperchaotic firing in Fig.6.
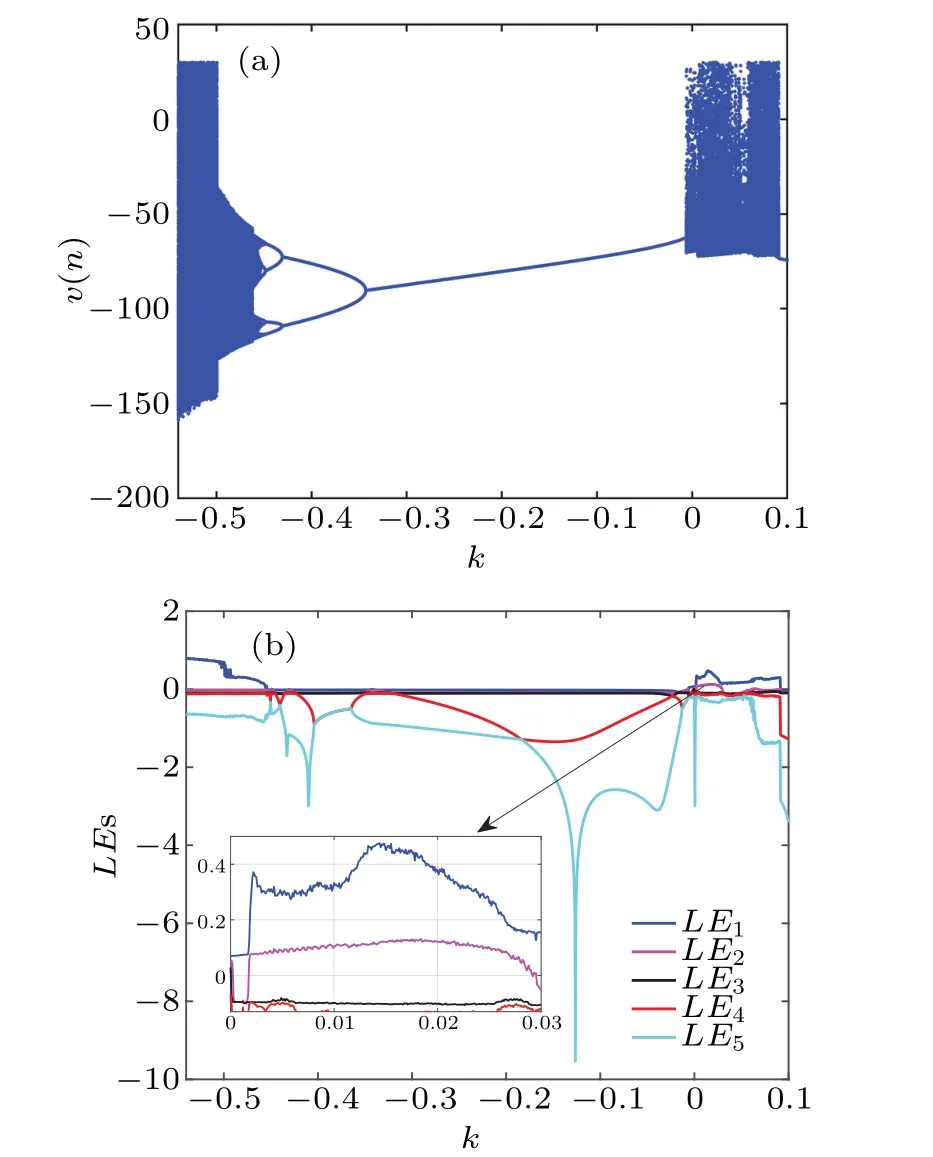
Fig.6.The dynamics of the network(6)with respect to the control parameter k with the initial parameters(-6,-1,1,1,1).(a)Bifurcation diagram.(b)Lyapunov exponents.
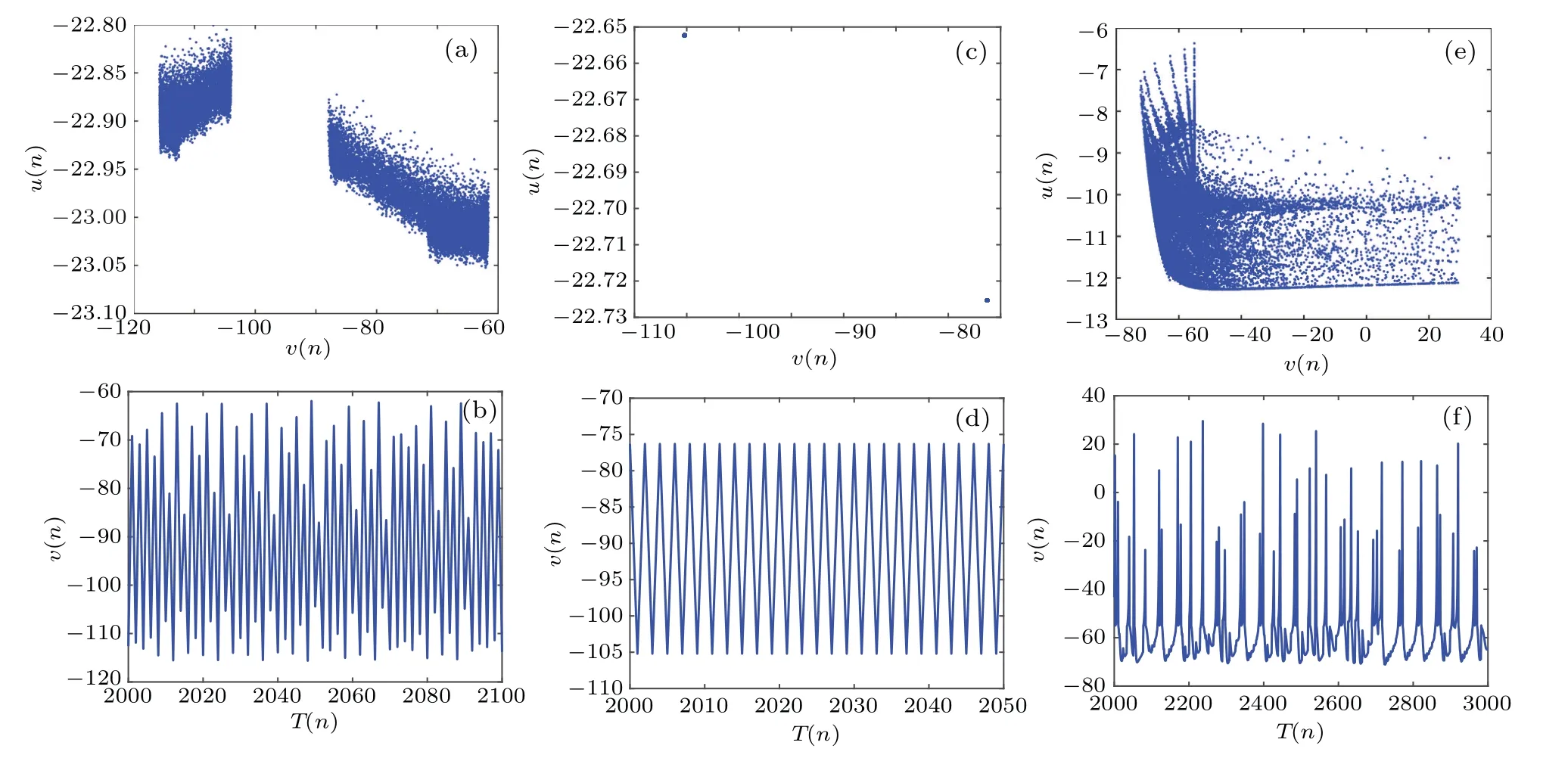
Fig.7.Phase diagrams on the v–u plane and time series of the variable v with different parameters k: (a) and (b) k=-0.46; (c) and (d)k=-0.4;(e)and(f)k=0.065.
4.2.Coexisting firing patterns
Two different coupling strengthsk=0.011, and-0.002 are selected as examples to demonstrate the coexisting firing patterns of the neuron network related to the initial value of the memristor.
Fork=0.011,figure 8(a)illustrates the Lyapunov exponents with respect to the initial value of the memristor.Whenϕ<0, all Lyapunov exponents are less than zero, meaning the neuron network is in a resting state.With the increase ofϕ, the Lyapunov exponentsLE1andLE2suddenly jump to positive values whenϕexceeds the critical valueϕ=0,resulting in the network transitioning from a resting state to a hyperchaotic firing pattern.Whenϕincreases toϕ= 2,the Lyapunov exponentLE1still remains positive value,whileLE2suddenly jump to negative values, resulting in the existence of one positive Lyapunov exponent,which indicates that the network transitions from hyperchaotic firing to chaotic firing.Figure 8(b) shows the phase diagram of the coexistence of resting state,hyperchaotic firing,and two different chaotic firing patterns.Note that in Fig.8(b), the red trajectory originates from the initial valueϕ=5, the blue fromϕ=3, the green fromϕ=1, and the cyan fromϕ=-1.The corresponding time series ofx(n) are illustrated in Fig.8(c).It is worth noting that although the all Lyapunov exponents remain unchanged whenϕ=5 andϕ=3, the network exhibit two heterogeneous chaotic firing patterns, which can be validated by the red and the blue phase diagrams in Fig.8(b) and the time series diagrams colored with the same colors in Fig.8(c).Similarly,whenk=-0.002,the network can exhibit the coexisting hyperchaotic firing,chaotic firing,and two resting states under different initial values,as depicted in Figs.8(d)–8(f).

Fig.8.The Lyapunov exponents,phase diagrams,and time series of coexisting attractors under two groups of different k values.(a)Lyapunov exponents for the initial value of the memristor at k=0.011.(b)The phase diagram of coexistence of chaotic attractors and resting state when k=0.011.(c) Time series diagram when k=0.011.(d) Lyapunov exponents for k=-0.002.(e) Phase diagram of coexistence of chaotic attractors and resting states at k=-0.002.(f)Time series diagram when k=-0.002.
4.3.Effects of noise on the network
We add the following noiseεξnto the internal state equation of the memristor in the neuron network.With the coupling and iteration of the discrete neuron network,the noise will act on the entire system.
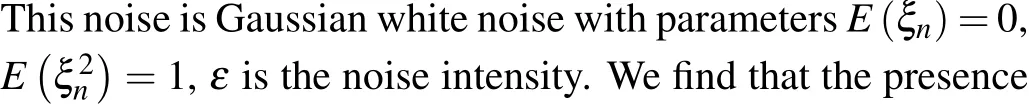

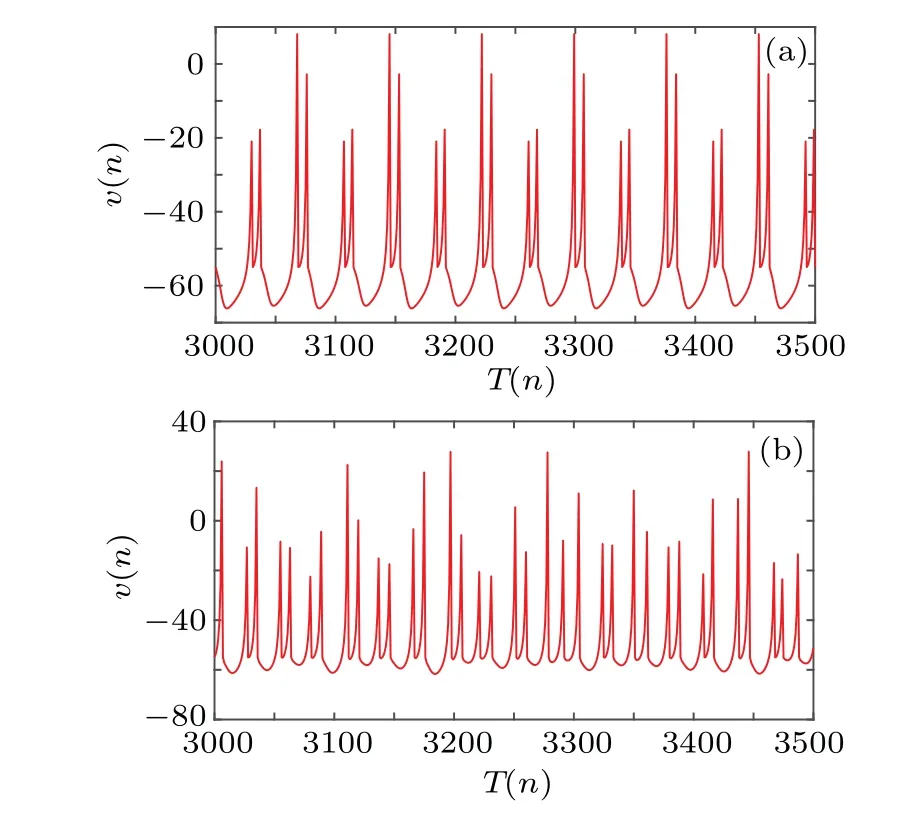
Fig.9.Time series diagram of membrane potential of Izhikevich neurons at k=0.1.(a)Periodic state in the absence of noise.(b)Chaotic state in the presence of noise.
5.Synchronization transition of heterogeneous neural networks considering noise
In order to study phase synchronization and synchronization transition of two different neurons coupled by the locally active discrete memristor,the definition of a phase is given as
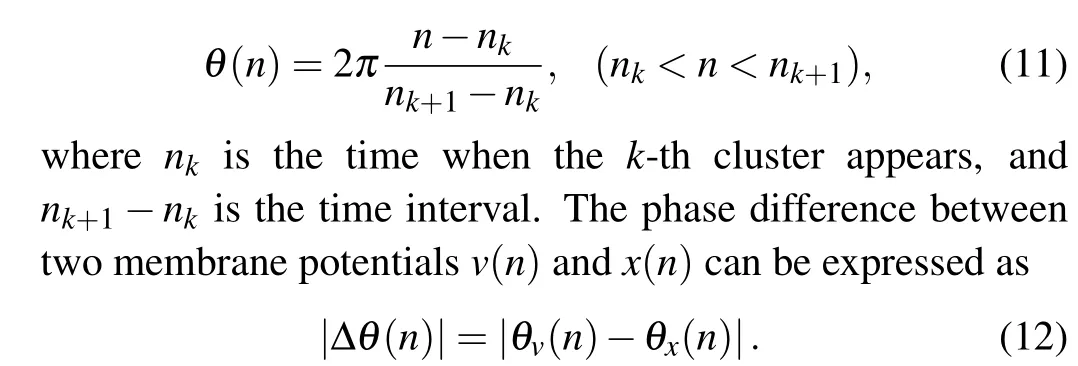
When the absolute value of the phase difference between two neurons is bounded by the value 2π, phase synchronization can be detected.We choose three differentkvalues to indicate synchronous transition behavior of the network.Whenk=0, the two neurons are uncoupled.In this case, the neuron Izhikevich exhibits a spiking firing pattern,while the Chialvo neuron exhibits a periodic firing pattern,as shown in Fig.10(a).It is observed that the firing patterns of the two neurons are obviously different.As depicted in Fig.10(b), the phase difference between the two neurons increases monotonously, validating that the two neurons are desynchronized.Whenk=0.44, the two neurons exhibit a quasi-synchronous burst firing pattern,as shown in Fig.10(c).In this case, the phase difference between two neurons is bounded by 2π.Whenkincreases tok=0.73 or more,the synchronous periodic spiking firing pattern emerges.Figure 10(e)shows the onsets of the action potential of the two neurons are consistent and figure 10(f) illustrates the phase difference is always 0.Thus, we can infer that the two neurons are completely phase synchronized.In addition,we found that appropriate noise can enable the network to achieve synchronization at a lower coupling strength.This has practical significance,because the large coupling strength does not conform to the biological reality.Whenk=0.4,figure 11 shows the time series and phase difference of two neurons.The red and blue trajectories in the figure represent the Izhikevich neuron, and the Chialvo neuron, respectively.When no noise is considered in the neuron network,The two neurons present an irregular chaotic firing pattern, as shown in Fig.11(a).The two neurons are desynchronized, which can be verified from the monotonously increasing phase difference of the two neurons in Fig.11(b).Then,the noise is added to the neuron network,it can be seen from Figs.11(c)and 11(d)that the two neurons are completely phase synchronized and the phase difference is always 0, which proves that the noise enables the neuron network achieve synchronization at a lower coupling strength.Note that when the noise intensity added to the neuron network is too large, the two neurons will return to the resting state.

Fig.10.Synchronization transition of heterogeneous neuron networks.(a)The time series of k=0.(b)Phase difference of two neurons when k=0.(c)The time series of k=0.44.(d)Phase difference of two neurons when k=0.44.(e)The time series of k=0.73.(f)Phase difference of two neurons when k=0.73.
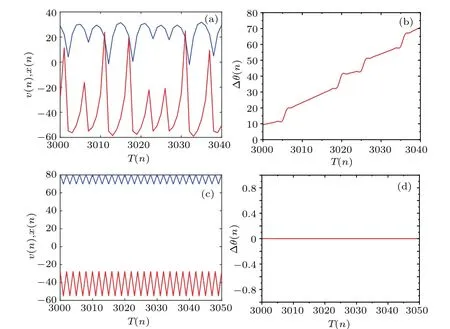
Fig.11.The time series of neuron membrane voltage and the phase difference between two neurons when the system is at k=0.4.(a) Time series in the absence of noise.(b)Phase difference in the absence of noise.(c)Time series in the presence of noise.(d)Phase difference in the presence of noise.
6.Conclusions
In this study,a discrete four-stable memristor is proposed and its locally activity and non-volatility are studied in detail.Then, the discrete Izhikevich neuron and Chialvo neuron is coupled by the memristor, a discrete heterogeneous neuron network model, thus, is established.The equilibrium points along with their stabilities are systematically analyzed.The coupling strength dependent dynamics are analyzed and it is found that the network can exhibit resting state,periodic firing,chaotic firing and hyperchaotic firing under different coupling strengths.The coexisting firing patterns, including the coexistence of resting state,two different chaotic firing and hyperchaotic firing, the coexistence of hyperchaotic firing, chaotic firing and two resting states are revealed.Furthermore,phase synchronization between two heterogeneous neurons are explored by varying the coupling strength and our results shows that the two heterogeneous neurons can achieve perfect phase synchronization at large coupled strength.What is more, the effects of noise on the network are also considered.We find that the presence of noise not only leads to the transition of firing patterns,but also achieves the phase synchronization between two heterogeneous neurons at a low coupling strength.
Acknowledgement
Project supported by the National Natural Science Foundations of China(Grant Nos.62171401 and 62071411).
杂志排行
Chinese Physics B的其它文章
- Quantum synchronization with correlated baths
- Preparing highly entangled states of nanodiamond rotation and NV center spin
- Epidemic threshold influenced by non-pharmaceutical interventions in residential university environments
- Dynamical behavior of memristor-coupled heterogeneous discrete neural networks with synaptic crosstalk
- Spatial search weighting information contained in cell velocity distribution
- Characteristics of cell motility during cell collision
