考虑横纵向误差协调的智能汽车路径跟踪控制研究
2024-02-28秦雪帅王旭东
秦雪帅,王旭东
重庆工商大学 机械工程学院,重庆 400067
1 引 言
轨迹跟踪控制作为无人驾驶中的关键技术,其目的是使车辆在保证稳定性与舒适性的前提下可以准确地按照给定的规划轨迹运行[1]。目前,国内外学者在轨迹跟踪控制上已经做出了大量研究,提出了一系列跟踪控制方法,主要可以分为两大类:基于模型预测的方法和基于几何追踪的方法。Wallace在1985年提出了纯跟踪控制算法(Pure Pursuit),纯跟踪控制算法是车辆横向控制算法中的一个代表,对于外界的环境变化具有较强的鲁棒性。在纯跟踪法中,由于预瞄点的确定与车辆速度紧密相关,所以在车速有显著变化时跟踪效果会变得很差。模型预测控制(Model Predictive Control)作为基于模型控制器的代表,由于具备便于添加各种空间状态变量的相关约束,控制精确度高等特点被广泛应用到无人驾驶车辆的跟踪控制当中。Falcone等[2]设计了一种基于线性模型的预测控制算法,使得模型预测控制的实时性得以提升,从而使得轨迹跟踪控制的精度和稳定性得以提高;陈龙等[3]提出一种基于非线性模型预测控制(NMPC)的纵横向综合轨迹跟踪控制方法,通过NMPC和障碍函数法(BM)的有效结合,提高了跟踪精度,改善了行驶稳定性。但由于MPC控制器在计算上比较复杂,随着运行状态约束、复杂度的增加,会使得MPC控制器的响应速度下降,无法满足无人驾驶车辆在实时性上的要求,这也是导致MPC控制器停留在学术研究而没有广泛应用到实际工程项目当中的主要原因。郭应时等[4]在神经工效学认知体系架构的基础上,融合模型预测控制算法(MPC)以及手臂肌肉模型,建立了一种基于神经工效学的车辆横向控制模型;张志勇等[5]采用模型预测原理设计了智能驾驶路径跟踪控制器,通过数据聚类结果来设计控制器的代价函数与约束条件;Chen等[6]提出了约束迭代LQR(CILQR),以有效解决具有一般约束形式的非线性系统动力学最优控制问题;Bae等[7]给出了一种可行的基于五阶贝塞尔曲线的自动驾驶车辆实时路径规划与跟踪方法,但是整体实时性较差;Feng等[8]提出了一种Bezier曲线与矢量场直方图(VFH)算法相结合的算法,利用VFH搜索方法搜索无碰撞状态,以Bezier曲线为参考线选取最优轨迹点。此外,常用的跟踪控制方法还包括线性二次调节器法(LQR)、比例-积分-微分控制(PID)法、前轮反馈控制(Stanley)法、滑模控制方法、自适应控制方法和模糊控制方法等。
上述的跟踪控制方法常运用在车速固定的场景下,无人驾驶车辆的行驶工况多较为复杂,车辆的纵向行驶速度处于一个动态变化的状态当中,固定车速下的跟踪会导致应用场景受限。同时,无人驾驶汽车属于常见的非完整性约束系统,车辆的横向控制与纵向行驶速度之间有密不可分的关系。在进行轨迹跟踪控制过程中,车辆的纵向速度控制效果将直接影响车辆对整个路径的跟踪效果。为了丰富无人驾驶车辆的应用场景,实现车辆横纵向联合控制以提升控制精度,本文针对无人驾驶车辆在结构化环境下的各种工况,设计了一种LQR与PID相结合的横纵向耦合控制器。LQR法相比于模型预测控制法(MPC),控制过程中没有设置各种空间状态变量约束,控制器的计算量大大降低,使用LQR法对车辆进行横向跟踪控制可以有效提升无人驾驶系统的实时性。另一方面,PID法虽然不能很好地处理多变量问题,但由于其计算量小,不用得到系统模型,因此在纵向控制过程中可应用其对车辆速度及位置误差进行控制调节,可以在保证跟踪控制精度的同时,提升系统的实时性。另外,本文在规划层面采用多项式曲线进行规划器的设计,以保证所规划轨迹满足车辆位置、速度及加速度的连续。
2 车辆跟踪误差模型的建立


图1 跟踪误差模型
为了得到跟踪误差模型,首先需要获得基于车身坐标系下的二自由度车辆动力学模型,即模型重点关注车辆沿Y轴的运动以及绕Z轴的转动;然后通过向量之间存在的关系,将其转化成自然坐标系下的误差模型[10],具体如图2所示。

图2 二自由度车辆动力学模型
对车辆进行受力分析,根据系统所受到的力和力矩平衡可以得到:
∑Fy⟹may=Fyf·cosδf+Fyr
(1)
(2)
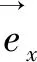
当轮胎侧偏角α较小时,轮胎的侧向力与轮胎的侧偏角近似呈线性函数关系[11],即Fy=Caα。故前后轮胎的侧向力分别为
Fyf=Caf·αf,Fyr=Car·αr
(3)
式(3)中,Caf和Car分别为前后轮胎的侧偏刚度。
由小角度假设可以近似得到[12]:
(4)
由式(1)—式(4)可以得到:
(5)
(6)


(7)

图3 车辆动力学模型转换
其中,k为道路曲率。
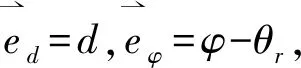
(8)
(9)
(10)
(11)
将式(8)—式(11)代入式(5)、式(6)中,经过化简后便可以得到基于自然坐标系下的误差微分方程:
3 规划及跟踪控制模块设计
3.1 多项式曲线规划
作为控制的上层模块,轨迹规划是整个无人驾驶车辆系统当中不可或缺的重要组成部分,其目的是生成一条可供无人车辆行驶的轨迹,并将轨迹输送至控制模块。
多项式曲线多应用于要求车辆在起始点以及目标点达到某种期望状态的场景当中。多项式曲线法是路径与速度耦合求解算法的一种,即在获得车辆行驶路径的同时,速度和加速度也随之获得[15]。本文中采用五次多项式曲线进行轨迹规划以保证生成的轨迹具备位置、速度、加速度连续的特性。
由于车辆不同于传统的自由移动机器人,不能单独做横向运动,其横向运动需要由纵向运动诱发,所以所规划的轨迹需要有切线斜率、曲率、速度以及加速度的要求[16]。因此在轨迹规划过程当中,需要做相应的修改,具体如下:
x(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5
y(x)=b0+b1x+b2x2+b3x3+b4x4+b5x5

关于轨迹的航向角及曲率通过下式可得:
θr(t)=arctan{y′[x(t)]}
至此轨迹规划模块便完成,生成的参考轨迹信息为

3.2 横向控制
线性二次调节器法(LQR)是多目标优化最优控制问题的代表性算法之一,目标函数可以表示为跟踪过程所产生的跟踪偏差与控制输入的累计加权之和[17],具体如式(12):
(12)
其中,err为状态变量,Q为半正定的状态加权矩阵,R为正定控制加权矩阵,为简化计算两者通常取为对角阵;Q矩阵元素影响着系统趋向稳定的速度,数值越大,系统相对快速趋向稳定;R矩阵元素影响着控制输入的大小,数值越大控制输入会相对减小,但加权矩阵并非越大越好。因此,第一项优化目标表示跟踪过程中累积路径偏差的大小,第二项优化目标表示跟踪控制过程中能量的损耗,这样就将轨迹跟踪控制问题转化为一个最优控制问题[18],本文中选取加权矩阵如下:
对于式(12)目标函数的优化求解,解出的最优控制规律u是关于状态变量err的线性函数:
uk=-[(R+BTPk+1B)-1BTPk+1A]err(k)=-Kerr(k)
其中,P是式(13)黎卡提方程的解[19]:
Pk-1=Q+ATPk(I+BR-1BPk)-1A
(13)

引入前馈控制之后:
其中,K3是通过LQR反馈控制计算出的矩阵K=[K1,K2,K3,K4]中的K3。
通过车辆实际位置与规划模块所得到的轨迹计算出误差量err;然后通过迭代的方式求解出黎卡提方程的解P进而求解出K,该步骤为求解LQR的关键所在;最后结合前馈控制求解出系统的控制量u=-K·err+δf,实现车辆的横向控制。
3.3 纵向控制
无人驾驶车辆纵向控制是通过控制车辆油门和刹车实现对车辆加速度的控制,实现车辆的加速和减速,使得车辆的实际位置、速度和加速度与规划模块所生成的轨迹一致。在整个控制过程当中,本文重点讨论车辆的跟踪效果而不对车辆行驶时的换挡过程以及发动机的能量损耗进行分析。因此,本文构建了理想的电机模型,即电机在达到最大转速之前以恒定扭矩运行,在达到电机最大转速之后以恒定功率运行。其中,功率P、扭矩M和转速n之间的关系满足P=2πn·M。整车的具体参数配置如表1所示。

表1 车辆参数表
(14)
对式(7)做进一步化简可以得到,车辆在自然坐标系下的纵向速度为
(15)
由于多项式曲线法是路径与速度耦合求解算法的一种,即在获得车辆行驶路径的同时,速度和加速度也随之获得。因此所规划的速度及加速度信息为
(16)
(17)
通过应用式(14)—式(17),本文设计了基于位置与速度误差的PID纵向控制模型,通过PID控制器参数的设置实现车辆在纵向上准确跟踪规划模块所生成的参考轨迹[20]。
3.4 横纵向联合控制
对于像无人驾驶车辆这样的非完整性约束系统,其行驶过程中的横向移动需要依靠车辆纵向移动的耦合触发。传统的控制方法在跟踪控制过程中,多设置车辆的纵向行驶速度为定值,然后进行轨迹跟踪,导致应用场景较为局限,不符合实际情况。为了实现无人驾驶汽车在变速行驶工况下的轨迹跟踪控制,由轨迹规划模块确定出车辆行驶的速度、路径参考曲线。纵向控制器根据车辆实际速度和位置信息与规划模块所计算出的轨迹信息之间的误差,运用PID控制策略计算并输出期望的速度与位置曲线,纵向控制器所输出的速度信息将作为横向控制器的输入量,从而形成横纵向协同控制系统,以实现无人驾驶汽车对整条规划轨迹的准确跟踪。图4展示了无人驾驶车辆横纵向控制流程图。

(a) 纵向控制流程图
由于车辆的横向移动需要依靠其纵向移动才可实现,所以无人驾驶车辆横纵向控制之间必然存在着耦合关系。为了实现对轨迹的准确跟踪,需要将横向控制和纵向控制二者之间进行有效融合。结合图4内容,实现了无人驾驶车辆的横纵向协同控制,具体如图5所示。整个系统由横向控制系统、纵向车速控制系统以及车辆平台三部分构成,通过该系统可以实现车辆在变速行驶过程中的轨迹跟踪。

图5 横纵向协同控制结构图
4 仿真分析
本文所建立的仿真工况均在结构化环境之下,重点对无人驾驶车辆的轨迹规划及跟踪效果进行分析讨论。相较于已有的控制方法对固定车速的跟踪控制,本文所采用的横纵向联合控制方式最大的优势在于可以有效解决无人驾驶汽车在变速行驶工况下的轨迹跟踪控制。为验证所建立规划器和控制器的性能,设置了泊车、驶入主路以及超车三种典型工况进行分析。
场景1:泊车是日常驾驶中常见的工作场景之一,这个过程驾驶员需要关注车辆四周的环境,同时泊车过程中需要兼顾车辆的油门和制动,这也在一定程度上加大了泊车的难度。高效的自动泊车系统可以提升泊车的效率。本文采用五次多项式曲线进行轨迹规划以保证生成的轨迹具备位置、速度、加速度连续的特性,同时生成的轨迹曲率连续可以保证整个过程的舒适性。在该场景中,设置车辆初始位置、速度和加速度均为零,即(x0,y0)=(0,0),v0=0 m/s,a0=0 m/s2;终点位置为停车位位置,终点速度和加速度为零,即vt=0 m/s,at=0 m/s2。整个泊车规划过程的误差、速度及位置信息如图6所示。

(a) 泊车误差
场景2:在城市道路驾驶的过程中,常遇到车辆由静止状态驶入主路的驾驶工况。在驶入主路的过程中,需要仔细观察主路后方的交通情况,在确保后方没车的情况下才缓慢汇入主路。同时在汇入主路的过程中,方向盘的幅度不可以打得太大,即车辆的航向角不可以过大。当车辆航向角θ较小时,车身与道路之间的夹角就小,这样可以保证车辆在汇入主路过程中即使有后方来车,后车也可以有一定空间进行缓冲,从而避免事故的发生。这就要求轨迹不仅要平滑,而且航向角要小。由于本文不涉及无人车的感知模块,所以设定汇入主车道时的车速vt=5 m/s,加速度at=0 m/s2。整个驶入主车道规划过程中的误差、速度、航向角以及横向位置信息如图7所示。
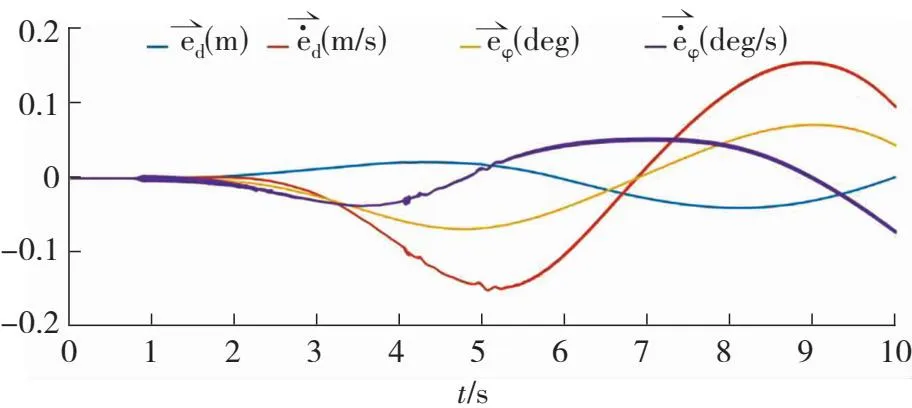
(a) 驶入过程误差
场景3:车辆在高速驾驶的过程中,常常需要进行超车,在超车过程中需要根据前车的行驶状况提升本车的车速进行变道超车。同汇入主路一样,在超车过程中,方向盘转动的幅度不可以太大,以免车辆产生较大的侧向加速度而发生横摆,因此所规划的轨迹航向角θ应该较小,同时整个超车过程应该在10 s内完成,以减小可能造成的安全隐患。本文设置超车完成时间为6 s,即t=6 s。由于本文不涉及无人车感知模块,对前车的行驶状态无法实时获取,故在此设置整个超车过程中车速由v0=20 m/s提升至vt=30 m/s,超车距离s=150 m。整个超车规划过程中的误差、速度、航向角以及位置信息如图8所示。

(a) 超车过程误差
5 结束语
本文针对智能车辆在结构化场景下的多种运行工况,设计了基于LQR与PID相结合的车辆横纵向耦合控制器。在横向控制层面,通过引入前馈控制量以消除系统的稳态误差,减小了车辆在实际运行过程中产生的横向误差,提升了控制过程的稳定性;在纵向控制层面,PID控制使得车辆的运行速度可以很好地与规划速度相匹配,且系统的稳态误差控制在一定的范围之内。
从具体的仿真实例中可以得出:无论是在具有较大转角的泊车工况下,还是低速驶入主路工况下或者是具有高速小转角的超车工况下,本文所设计的横纵向耦合跟踪控制器都具有较好的跟踪效果,系统误差都控制在可接受的范围之内。因此,本文所设计的智能车辆轨迹跟踪控制器可以很好地应用于机场、港口等结构比较固定的场景当中。
智能车辆是集感知、决策和控制于一体的集成系统。因此在今后的研究当中,需要考虑将感知与规划进行有效融合以实现更为智能的轨迹规划。同时,非结构化场景路况复杂,环境多变,本文所设计的跟踪控制器是否可以适用仍需要深入探讨。
