基于DYCORS算法的OVA-SVM参数优化与应用研究

余晨曦,尹彦力

重庆师范大学 数学科学学院,重庆 401331

1 引 言

支持向量机(SVM)是一种常见的二元分类模型,它分为硬间隔SVM、软间隔SVM、核化SVM等,主要用于模式识别、数据分析、分类问题等领域。由于SVM通常能解决二元分类问题,因此它在解决多元分类问题时需要先将其转化为二元分类问题,再用SVM进行分类。对于二元分类问题,通常将能使数据完美分成两部分的分割面称为超平面,二维空间中的超平面是一条直线,三维空间中的超平面是一个平面。SVM的目标就是寻找一个最优超平面,使得所有数据点都尽可能地远离此分割平面,从而将一个空间中不同类别的数据完美地分为两类。

一对多法(One Versus All,简称OVA)[1]是最早的基于SVM对多类别进行分类的方法,其思想是将多类别问题转化为两类别问题来实现。

OVA-SVM是把支持向量机(SVM)和One Versus All(OVA)方法结合后提出的一个多类别分类判别模型,其性能依赖于模型参数的选择,其参数包括惩罚参数C、核函数类型k(k,kernel)、RBF核函数参数γ(γ,gamma)、ploy核函数的参数d(d,degree),以及迭代终止参数t等。如何选取最优的参数设置,进一步提升模型性能至关重要。OVA-SVM是目前应用比较多的一种机器学习模型,具有良好的泛化能力,其性能依赖于超参数的选择。当前较为常见的超参数优化方法有手动调参、网格寻优、随机寻优、贝叶斯优化方法、基于梯度的优化方法、进化寻优等。

手动调参,即研究者们通过一步步地手动调节超参数来实现对其的优化。研究者们可以判断如何设置超参数可以获得更好的模型效果,但这一方法依赖大量的经验,且人工调节较为耗时。

网格寻优,王兴玲等[2]将网格搜索用于向量机核函数的参数确定问题。使用网格寻优,首先需要为每一个超参数构建其各自的模型,再对各个模型的性能进行评析,从而获得性能最佳的模型和最优超参数。其优点在于该方法中的所有样本均能得到验证;其缺点在于当超参数的个数较多时,计算量会直线上升,比较耗时,并且这一方法无法保证能获得最优的超参数值,也难以保证能获得全局最优解。

随机寻优,Droste等[3]对黑盒优化中随机搜索启发式算法进行了研究。该方法可以基于时间和计算资源情况,选择合理的计算次数,并控制组合的数量,在超参数网格的基础上随机选择组合来训练模型。通常情况下,随机寻优方法可以分辨哪些超参数对模型性能影响最大,从而优先获得这些超参数的最优值。与网格寻优相比,该方法能更快地找到最优参数,也能通过较少的迭代次数获得正确的参数设置;其缺点在于它只适用于低维数据情况,并且只能够针对单独的超参数组合模型进行训练,并评估各自的性能。

贝叶斯优化,Shukla等[4]提出通过贝叶斯优化算法自动设置超参数,走向自主强化学习。该方法通过构造一个函数的后验分布来工作,它可以在前一模型的基础上对后一模型的超参数选择产生影响,在一定程度上解决了模型独立时,各模型之间失去联系的问题。随着观测次数的增加,后验分布得到改善,算法更加确定参数空间中哪些是值得探索的区域,哪些是不值得探索的区域。其优点在于该方法通过不断采样来推测函数的最大值,但采样点不多;其缺点在于容易陷入局部最优值的区域内重复采样,难以找到全局最优解,并且需要进行多次迭代,时间长且成本高。

基于梯度的优化方法,Lu等[5]提出基于梯度下降法的机器学习增强优化方案。该方法应用场景并不广泛,主要通过梯度下降算法对超参数进行优化。其优点在于梯度下降算法并不高的计算量,使其可以应用于大部分高规模数据集中;其缺点在于由于超参数优化通常是非凸的,并不是一个完全平稳的过程,所以这一方法的应用场景并不广泛,难以在各场景中找到全局最优解。

进化寻优,严盛雄[6]提出了基于进化算法的LCL型滤波器参数优化设计。该算法是一个动态过程,类似于自然进化中不断变化的环境,它经常被用来寻找其他技术不易求解的近似解。由于优化问题可能太耗时并且计算资源占用很大,因此通常难以找到精确的解决方案,在这种情况下,进化算法通常可以找到一个局部最优解。其优点在于可以产生出不受人类偏见影响的解决方案;其缺点在于不能保证找到全局最优解,没有可靠的算法终止条件和足够的理论基础,并且算法复杂度较高,容易造成资源的消耗。

综上所述,现有的参数优化方法多样,但普遍还存在以下问题:时间成本较大,内存占用较大,难以解决高维数据情况,难以找到全局最优解。现有工作表明:OVA-SVM的性能高度依赖其模型参数的选择,如何选取最优的参数设置,进一步提升模型性能至关重要,而DYCORS算法可以在节约时间成本和内存的前提下,对高维数据问题也能找到全局最优解。故本文针对现有参数优化方法存在的问题,提出针对OVA-SVM模型参数分块优化的YDYCORS算法,该算法在参数优化过程中,与现有方法相比更高效,使用范围更广,更易找到全局最优解。

2 DYCORS算法与参数优化过程设计

2.1 DYCORS算法

DYCORS算法由Regis等[7]提出,算法结合了动态坐标扰动与算法重启策略,是目前最有效的昂贵“黑箱”函数优化算法之一。对于大部分测试函数,DYCORS 算法最终都能求得目标函数值。大部分高维问题最有效的算法还是DYCORS,它不仅能解决上文中提到的时间成本与内存占用较大的问题,而且也能适用于高维数据的情况,并得到全局最优解。该算法通过动态坐标扰动,每次按照扰动概率(一个单调递减的函数)对当前最优点的每一维坐标进行扰动,以此获得一个新的采样点。本文将该算法应用于OVA-SVM的参数优化问题,以提升OVA-SVM的性能。其中DYCORS算法如表1所示。

表1 DYCORS算法框架

扰动概率φn(对应Step5)是关于迭代次数n0≤n≤Nmax-1的严格单调递减函数,其计算表达式为

由于φn表示概率,所以其函数值在[0,1],并且φ0=1。Step7和Step8是从候选点中选出最有潜力的点作为新的采样点,通过计算每一个候选点的函数值度量Vev(t)与距离度量Vdm(t)作为其度量标准,函数定义如下:

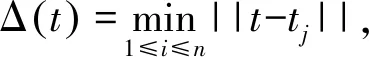
DYCORS算法可以在减少迭代次数的前提下,对于高维数据问题也能找到全局最优解,故本文拟采用DYCORS算法调节OVA-SVM的惩罚参数C、核函数类型k、RBF核函数参数γ、ploy核函数参数d以及迭代终止参数t等,获得较现有方法更优的参数配置,进一步提升模型性能。

2.2 参数优化过程设计

针对OVA-SVM参数优化时出现的问题,提出优化后的参数调节方法,提升模型性能,本文的主要贡献包含以下两个方面:

(1) OVA-SVM模型的性能十分依赖于模型参数的选择,而该模型需要调节的参数有惩罚参数C、核函数类型k、RBF核函数参数γ、ploy核函数参数d以及迭代终止参数t,这些参数中既包含整数又包含连续实数,并且模型本身的训练时间成本也较高。而运用DYCORS算法进行参数调节可以减少迭代次数,并且对整数和连续实数超参进行优化,因此DYCORS算法是适用于OVA-SVM模型参数优化的方法。

(2) 由于同时调节5个参数计算量较大,可能难以找到全局最优解,因此本文针对OVA-SVM参数优化时出现的问题,在DYCORS算法的基础上进行参数分块调节,提出了改进后的YDYCORS算法。该算法先用DYCORS调节对OVA-SVM的性能影响最大的参数:惩罚参数C、核函数类型k、RBF核函数参数γ;再固定最优惩罚参数C、核函数类型k、RBF核函数参数γ,用DYCORS调节剩余参数中影响较大的参数:ploy核函数的参数d与迭代的终止参数t;最后再用DYCORS一起调节已获得的5个最优参数。先对参数进行分析,再对参数进行分块调节,可以在避免出现计算量过大的前提下,提升参数优化的效果。

本文中运用DYCORS算法优化参数的主要过程如图1所示。

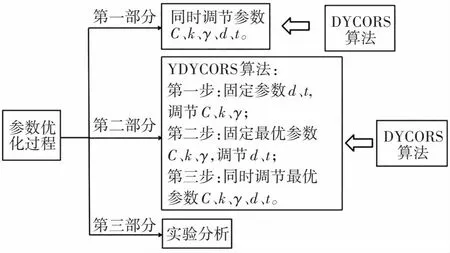
图1 运用DYCORS算法优化参数的主要过程

2.3 OVA-SVM模型的参数影响分析

影响OVA-SVM性能的参数主要有惩罚参数C、核函数类型k、RBF核函数参数γ、ploy核函数参数d以及迭代的终止参数t等。

惩罚参数C[11],即对误差的宽容度,表示对离群点的重视程度。C越大,表示重视程度越高,允许它们被分类错误率高;C越小,表示重视程度越低,允许它们被分类错误率低。

核函数[12]的引入是为了将高维空间中的内积运算转化至低维空间,从而解决线性不可分问题。核函数的选取,使得线性不可分的样本通过映射至更高维的空间中而变得线性可分,并且能解决映射过程中由于样本维数过高而造成的“维数灾难”,在操作过程中也可以忽略低维向高维映射函数的计算,只需计算低维空间中的核函数即可。常见的核函数类型(x,y表示输入空间的向量)如表2所示。

表2 常见核函数类型

3 基于DYCORS算法的OVA-SVM参数优化

本文涉及的参数主要有惩罚参数C、核函数类型k、RBF核函数参数γ、ploy核函数参数d、迭代终止参数t。

针对现有超参数优化方法在调节OVA-SVM参数过程中存在的时间成本较大、内存占用较大、难以解决高维数据,且难以找到全局最优解等问题,提出运用DYCORS算法调节OVA-SVM参数的方法。以下将从DYCORS算法对参数C、k、γ、d、t同时调节,并对其参数优化过程进行分析。

3.1 DYCORS同时调节参数C、k、γ、d、t

DYCORS算法与现有的手动调参、网格寻优、随机寻优、贝叶斯优化方法、基于梯度的优化方法、进化寻优等超参数优化方法相比,可以更高效地完成参数优化,减小内存占用空间,同时能适用于高维数据问题,得到全局最优解,故DYCORS是一种十分适用于OVA-SVM参数优化的方法。

为实现DYCORS算法对OVA-SVM参数的优化,进一步提升OVA-SVM的性能,本节将运用DYCORS算法同时调节惩罚参数C、核函数类型k、RBF核函数参数γ、ploy核函数参数d以及迭代的终止参数t。

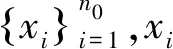
3.2 YDYCORS算法的参数优化过程

由于同时调节5个参数计算量较大,可能难以获得全局最优解,因此本节对原有的DYCORS算法进行优化,提出改进后的YDYCORS算法。YDYCORS算法对5个参数进行了分块,将调参过程分为了以下3个步骤:第一步,固定ploy核函数参数d与迭代终止参数t,用DYCORS同时调节惩罚参数C、核函数类型k、RBF核函数参数γ;第二步,在固定最优惩罚参数C、核函数类型k、RBF核函数参数γ的前提下,用DYCORS同时调节ploy核函数参数d与迭代终止参数t;第三步,用DYCORS同时调节最优惩罚参数C、核函数类型k、RBF核函数参数γ、ploy核函数参数d以及迭代终止参数t。

3.2.1 固定参数d、t,DYCORS同时调节参数C、k、γ

据研究表明[8],惩罚参数C、核函数类型k以及RBF核函数参数γ很大程度上影响了OVA-SVM的性能,惩罚参数C通过影响学习机器置信范围和经验风险的比例,进而影响OVA-SVM的泛化能力,核函数类型与核函数的参数通过影响样本被映射到特征空间的复杂程度,进而影响OVA-SVM的性能。因此在提升OVA-SVM模型性能的过程中,惩罚参数C、核函数类型k以及RBF核函数参数γ较其他参数更为重要。故第一步先固定参数d、t,此时d、t的参数值是任意设置的,再运用DYCORS算法先对参数C、k、γ进行调节,具体步骤同上一节。

3.2.2 固定最优参数C、k、γ,DYCORS同时调节参数d、t

第二步选择多项式核函数作为OVA-SVM的核,因此除惩罚参数C、核函数类型k以及RBF核函数参数γ以外,ploy核函数参数d和迭代终止参数t对OVA-SVM性能的影响较大。因此,固定上一小节得到的最优惩罚参数C、核函数类型k以及RBF核函数参数γ,运用DYCORS算法同时调节ploy核函数参数d和迭代终止参数t,具体步骤同上一节。

3.2.3 DYCORS同时调节最优参数C、k、γ、d、t

在经过前两步的参数调节后,OVA- SVM参数优化的效果得到了进一步提升。为了使效果达到最佳,本小节利用参数之间的相互依赖性,在第三个步骤中用前两步获得的最优参数为初始参数值,同时调节最优惩罚参数C、核函数类型k、RBF核函数参数γ、ploy核函数参数d以及迭代终止参数t,具体步骤同上一节。

4 实验验证与结果分析

4.1 数据集

MNIST数据集[9]来自美国国家标准与技术研究所, National Institute of Standards and Technology (NIST),是NIST数据库的一个子集,也是机器学习中评估模型性能时常用的数据集。MNIST数据集分为训练集与测试集,训练图片一共有60 000张,可采用学习方法训练出相应的模型,测试图片一共有10 000张,可用于评估训练模型的性能。

IRIS数据集[10],也称鸢尾花卉数据集,其中共包含150个样本数据,该数据集是机器学习中常见的数据集,共分为以下3类:山鸢尾(Iris Setosa)、杂色鸢尾(Iris Versicolour)、维吉尼亚鸢尾(Iris Virginica)。该数据集以鸢尾花的特征作为数据来源,包含4个特征:花瓣长度、花瓣宽度、花萼长度、花萼宽度。IRIS数据集是一类多重变量分析的数据集,也是在数据分类中十分常用的测试集和训练集。

4.2 评估指标

本文实验的评估指标[9]主要是准确率,为阐述准确率(Acc)的含义,先介绍以下两个概念:

TP(True Positives):表示模型将正实例预测为正实例的数据个数,用NTP表示;TN(True Negatives):表示模型将负实例预测为负实例的数据个数,用NTN表示;准确率指标的公式:

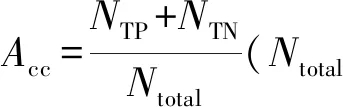
4.3 实验环境

本文实验在具有64 GB内存和NVIDIA GeForce GTX 1050 Ti GPU和Intel(R) Core(TM) i7-8750H CPU的个人工作站上进行。

4.4 实验结果

针对现有方法存在的4个问题,设计如下实验:第一部分,手动调节OVA-SVM参数,获得在该参数设置下的模型准确率;第二部分,运用DYCORS算法同时调节参数C、k、γ、d、t,获得在该参数设置下的模型准确率;第三部分,首先固定参数d、t,运用DYCORS算法调节参数C、k、γ,然后固定最优参数C、k、γ,调节参数d、t,最后同时调节最优参数C、k、γ、d、t,获得在该参数设置下的模型准确率。本实验针对MNIST和IRIS两个数据集,将DYCORS算法运用于OVA-SVM的参数优化中,其中先确定各参数的取值范围:C的取值范围为[0, 10],k的取值范围为[linear, poly, rbf, sigmoid],γ的取值范围为[0, 10],d的取值范围为[0, 5],t的取值范围为[0.000 1,0.001],经过以上实验后可得如表3、表4中的结果。

表3 在MNIST数据集上的实验结果(60%训练,40%测试)

表4 在IRIS数据集上的实验结果(60%训练,40%测试)

如表3在MNIST数据集上的实验结果所示:运用DYCORS算法调节OVA-SVM模型的参数时,由于同时调节5个参数工作量较大,得到的模型准确率为98.19%,但在运用YDYCORS算法调节OVA-SVM模型的参数后,模型准确率达到了98.61%,能得到更好的效果。

由表4在IRIS数据集上的实验结果可知:在运用DYCORS算法和YDYCORS算法调节OVA-SVM的参数时,都能得到较高的准确率与良好的模型效果。为了更清晰地反映模型准确率在不同数据集与不同调参方法下的具体情况,本文再将上述两个数据集的实验结果进行对比,如表5所示。

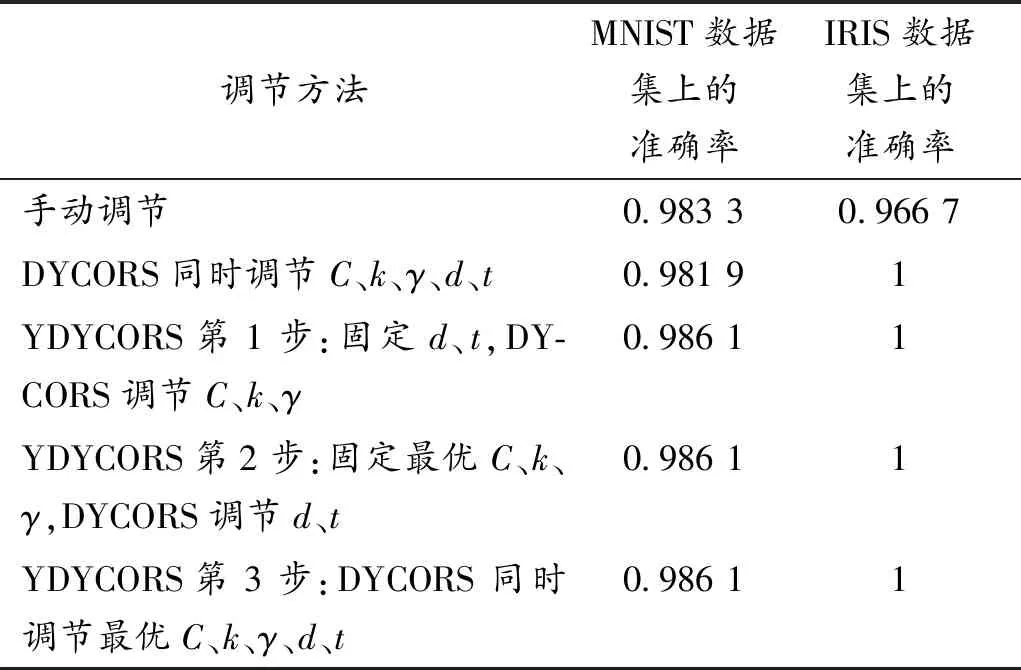
表5 两个数据集上的实验结果对比

通过MNIST和IRIS两个数据集上的实验结果对比可以发现:由于数据集的选择不同,呈现的模型准确率也不同,明显在IRIS数据集上的模型准确率更高,但在MNIST数据集上,YDYCORS算法的优势体现得更明显。运用DYCORS算法直接同时优化5个参数,计算量较大,可能无法断定是否能得到较高的模型准确率,但在运用YDYCORS算法对OVA-SVM的参数进行分块调节后,能得到与手动调参和直接用DYCORS同时调节5个参数相比更高的模型准确率,从而也能进一步提升其模型性能。综上实验,可以进一步说明本文提出的YDYCORS算法可以在一定程度上解决现有超参数优化方法还存在的问题,因此本文对OVA-SVM参数的优化也取得了比较理想的效果。

5 结论及展望

5.1 结 论

本文针对现有的超参数优化方法存在的时间成本较大,内存占用较大,难以解决高维数据,难以找到全局最优解等问题,运用DYCORS算法对模型影响较大的惩罚参数C、核函数类型k、RBF核函数参数γ、ploy核函数参数d以及迭代终止参数t这5个参数进行调节,提出将参数进行分块调节的YDYCORS算法:先用DYCORS调节对OVA-SVM的性能影响最大的参数:C、k、γ;再固定最优参数C、k、γ,用DYCORS调节剩余参数中影响较大的参数d和t;最后用DYCORS一起调节已获得的5个最优参数。先对参数进行分析,再对参数进行分块调节,可以在避免出现计算量过大的前提下,提升参数优化的效果。

通过MNIST和IRIS两个数据集上的实验结果对比可以发现:运用DYCORS算法直接同时优化5个参数,由于计算量较大,可能无法断定是否能得到较高的模型准确率,但在运用YDYCORS算法对OVA-SVM的参数进行分块调节后,能得到与手动调参和直接用DYCORS同时调节5个参数相比更高的模型准确率,从而也能进一步提升模型性能,取得了较佳的模型效果。

5.2 展 望

虽然本文提出的方法可以在一定程度上解决现有超参数优化方法存在的问题:如时间成本较大、内存占用较大、难以解决高维数据问题、难以找到全局最优解,但该方法能否解决超参数优化中可能存在的其他问题还有待研究。另外,本文只对惩罚参数C、核函数类型k、 RBF核函数参数γ、ploy核函数参数d和迭代终止参数t进行优化,而如何更全面地优化OVA-SVM的参数还值得未来进一步探索。同时,本文提出的YDYCORS算法只对5个参数进行了一种形式的分块,其余的分块形式能否取得更佳的模型效果还值得研究。