基于改进PCA的复杂多阶段过程故障检测

冯立伟，郭少锋，吴弋飞，邢 宇，李 元

（1.沈阳化工大学理学院，辽宁沈阳 110142；2.沈阳化工大学计算机科学与技术学院，辽宁沈阳 110142；3.沈阳化工大学信息工程学院，辽宁沈阳 110142）

为满足人们对系统安全性、可靠性的不断增长的期望和需求，基于数据驱动的过程控制和故障检测技术得到了广泛的应用[1-2]。

过程的多阶段、动态性和非线性特征都是常见的导致故障难以检测的重要原因[3-4]。具有动态性的过程变量随时间变化，靠前时刻的样本影响靠后时刻的样本，前后时刻的样本间存在时序上的相关性。为此Ku等人提出了动态主元分析（dynamic principal component analysis,DPCA)[5]，RATO等人对时滞参数的选取进行了进一步的研究[6]。DPCA利用构造时滞矩阵的方式来减弱前后时间点样本之间的时序关联，部分克服了动态性的影响。但未考虑多阶段和非线性问题。针对非线性和多阶段特征的影响，He等提出了基于k 近邻规则（k nearest neighbor rule,kNN)[7]的故障检测方法，但该方法无法处理疏密程度不同的多阶段问题。Breunig 等提出基于局部离群因子（local outlier factor,LOF)[8]的故障检测方法克服了此问题。此外，Ma 等人提出了基于局部近邻标准化和主成分分析（local neighbor standardization and principal component analysis,LNS-PCA)[9]的故障检测方法。LNS 能够转化多阶段过程数据为近似服从标准正态分布的单一阶段的数据，成功克服多阶段和非线性的影响。但上述故障检测方法又未考虑动态性的影响。

针对上述问题，提出了基于时空近邻标准化和主成分分析（time-space nearest neighborhood standardization and principal component analysis，TSNSPCA）的故障检测方法。通过TSNS 处理使该过程数据近似服从单一阶段的多元高斯分布，并分离故障样本，然后再使用PCA对过程进行故障检测。

1 主成分分析

设X∈Rm×n，m表示样本个数，n表示变量个数，对X进行Z-score标准化后为X0。PCA可以将X0分解为：

其中T∈Rm×r和P∈Rn×r分别是X0的得分矩阵和负载矩阵，r是选取的主元个数。是残差矩阵。

T2和SPE统计量是用于检测异常情况的常用过程监控指标。对于新样本g∈R1×n，计算其T2和SPE统计值。

采用核密度估计技术来计算T2和SPE统计量的控制限，并基于测试样本的统计值是否大于控制限的值来判断过程是否发生异常。

2 时空近邻标准化和主成分分析的故障检测

2.1 时空近邻标准化

TSNS 能够将多阶段数据高斯化为单一阶段的数据，分离故障样本，同时去除前后时刻样本间的时序相关性[10-11]。

TSNS 的主要步骤以一个样本u为例进行说明。首先，计算u的时间上前N 近邻集Nt(u)，该近邻集中的样本按照时序距离大小升序排列。

计算Nt(u)中每个样本的空间上前K 近邻集Ns(ut)，ut代表u的时间上第t 近邻样本，t∈[1,N]。Ns(ut)中的样本按照空间中欧式距离的大小升序排列。

求出N 个空间近邻集Ns(ut)的均值m(Ns(ut))和标准差s(Ns(ut))。

使用N 个空间近邻集的均值和标准差对样本u进行时空近邻标准化。

通过TSNS将具有动态性和非线性特征的多阶段过程数据转化为近似服从单一阶段的多元高斯分布的数据，并剔除过程的动态性，使故障更容易被检出。

2.2 时空近邻标准化和主成分分析故障检测步骤

过程正常运行时采集数据作为训练集，过程运行时引入故障获得测试集。TSNS-PCA 对过程进行故障检测的步骤如下：

离线建模：

①计算每个训练样本时间和空间上的近邻信息，并求出空间上近邻信息的均值和标准差，通过（8）式分别对各阶段的训练样本进行标准化。

②使用PCA通过（1）式将TSNS处理后的训练数据进行分解，求出负载矩阵和得分矩阵。

③通过（2）和（3）式分别计算出每个训练样本的T2和SPE统计值，并使用核密度估计确定T2和SPE的控制限。

在线检测：

①使用相同时刻训练样本的近邻信息对测试样本进行时空近邻标准化。

②使用建模过程中得到的负载矩阵和得分矩阵通过（2）和（3）式计算每个测试样本的T2和SPE统计值。

③将测试样本的统计值与建模时得到的控制限进行对比判断过程是否出现故障。

3 青霉素发酵过程的故障检测

使用Pensim 仿真平台[12]模拟青霉素发酵过程产生实验数据，多项研究[13-14]已经证明该平台实用性非常出色。该平台共给出了18个变量来控制仿真，选取其中12个重要的变量[15]进行实验，变量选取见表1。

表1 青霉素发酵过程选取变量

设置仿真时长400h，采样间隔1h。过程正常状态下采集一批数据作为训练集。通过在前3 个变量上添加阶跃、斜坡两种扰动设置6 种故障，起止时间皆为51-400h，故障描述见表2。对应生成6个批次的测试集。

使 用PCA、DPCA、kNN、LOF、LNS-PCA 和TSNS-PCA 方法分别对青霉素发酵过程进行故障检测，置信度都取97%。PCA、DPCA、LNS-PCA和TSNS-PCA 根据得分贡献率不低于90%的要求分别选取主元个数为5、6、8、7。DPCA 设置时滞参数l为3。kNN 和LOF 均设置近邻数k 为4。LNSPCA 设置近邻数K 为7。TSNS-PCA 设置时间近邻数N 为4，空间近邻数K 为7。测试集的故障检测率见表3。

表3 测试集的故障检测率 单位/%

从表3 可以看出所有方法对f1-f3 批次中的故障检测率均较高，对于f4-f6 批次中的故障，TSNSPCA 具有最高的故障检测率。

以f4 批次为例分析所用方法故障检测效果好坏的原因，f4 批次的故障发生在搅拌功率上。从图1(a）部分变量的空间散点图可以看出青霉素发酵过程是一个具有非线性特征的多阶段过程。图2(a）空气流量的自相关系数图表明过程前后时刻样本间存在显著的时序相关性。PCA、DPCA 的故障检测都假设过程数据服从单一阶段的多元高斯分布，且要求过程数据必须是稳态的，实验数据不符合条件，故检测率低。kNN 和LOF 分别使用与近邻样本的欧式距离平方和以及相对密度作为统计量，都能对具有非线性特征的多阶段过程进行故障检测。LOF 考虑了疏密程度因素的影响，所以故障检测率要高于kNN。但两者均未考虑时序相关性的影响问题，故检测率欠佳。

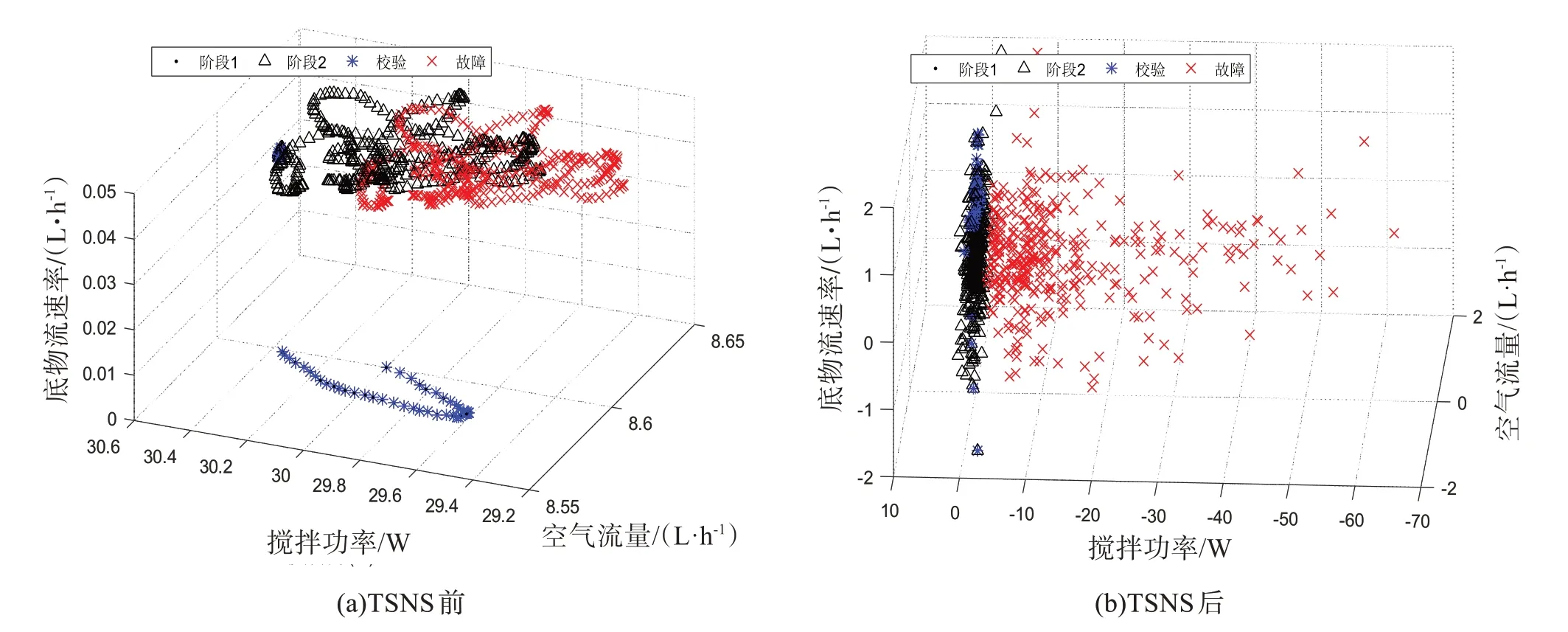
图1 TSNS前后部分变量的空间散点图

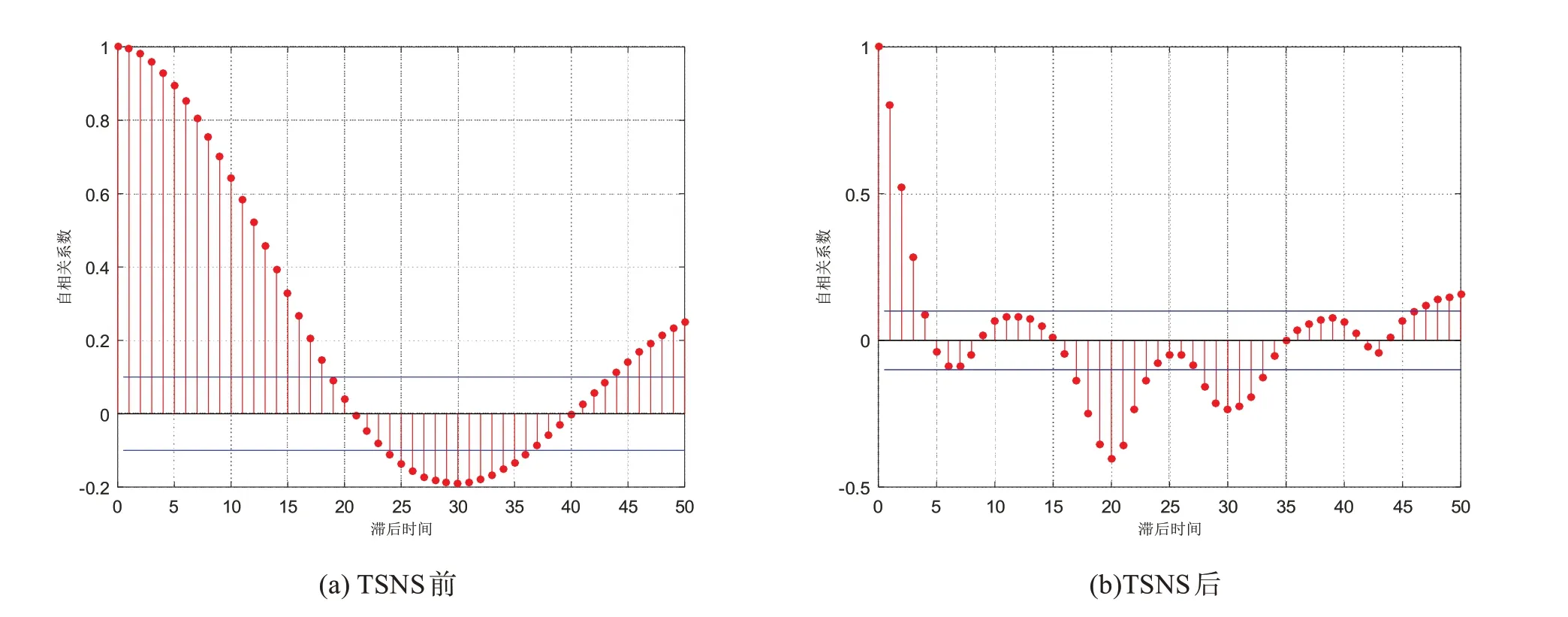
图2 TSNS前后空气流量的自相关系数图

TSNS 相较于LNS 在标准化时加入了时间信息，能够帮助分离空间上正常而时间上发生偏离的故障样本。故TSNS-PCA 的故障检测率高于LNS-PCA。图1（b）为TSNS 后部分变量的空间散点图，多阶段数据被转化为了单一阶段的数据，且故障被明显分离了出来。图2（b）为TSNS 后空气流量的自相关系数图，时序相关性被显著降低了。TSNS 后底物浓度、溶解氧浓度、菌体浓度的频率分布见图3。TSNS 后的数据近似服从单一阶段的多元高斯分布，满足了PCA 故障检测方法对过程数据的假设条件，所以TSNS-PCA 的故障检测率很高，如图4。

图3 TSNS后变量8、9、10的频率分布图

图4 TSNS-PCA对f4批次测试集的故障检测图

TSNS 将复杂多阶段过程数据转化为近似服从单一阶段的多元高斯分布的数据，并剔除过程的动态性特征，能够提升PCA在故障检测方面的能力。

4 结论

在实际工业生产中，生产过程往往变得越来越复杂，不再具有单一特征。传统的故障检测方法往往无法有效监控这种复杂的多阶段过程。TSNSPCA 方法采用了TSNS 预处理技术来使得过程数据更符合PCA 方法的要求，从而显著提高了故障检测率。TSNS-PCA 能够更好地保证过程的安全性和可靠性。