基于多阶解析信号的磁源变深度成像方法

王彦国 田野 邓居智 葛坤朋 陈晓

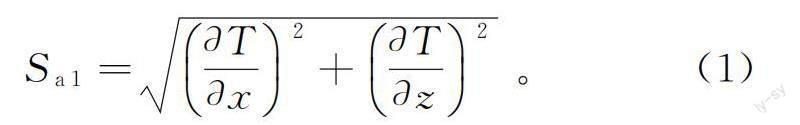
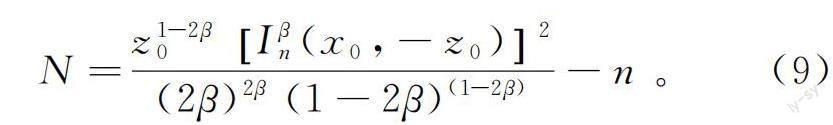
摘要：解析信号是磁法数据处理与解释的常用工具。本文从不同阶次解析信号及其垂向导数关系出发，引入深度缩放因子，构建了磁源变深度成像函数。该方法利用深度成像的极大值反映场源空间位置，利用反演深度及成像极大值估计场源构造指数。另外，结合不同深度缩放因子、不同阶次的成像结果提高方法的可靠性与适用性。模型试验及实例应用表明，相对于解析信号比值和局部波数的DEXP（depth from extreme points）方法，本文方法在使用更低阶次导数的情况下，能够获得更强的计算稳定性、更高的空间成像分辨率和更准确的场源参数反演结果。

关键词：磁源；解析信号；深度成像；构造指数

doi：10.13278/j.cnki.jjuese.20220338

中图分类号：P631.2

文献标志码：A

收稿日期：2022-12-11

作者简介：王彦国（1985—），男，副教授，硕士生导师，主要从事重磁数据处理与反演解释，E-mail：201360026@ecut.edu.cn

基金项目：国家自然科学基金项目（41504098，41862013）；江西省自然科学基金项目（20212BAB203005）

Supported by the National Natural Science Foundation of China （41504098， 41862013） and the Natural Science Foundation of Jiangxi Province （20212BAB203005）

Magnetic Source Variable Depth Imaging Method Based on

Different Order Analytic SignalsWang Yanguo^{1， 2}， Tian Ye²， Deng Juzhi^1，2，Ge Kunpeng^{1， 2}， Chen Xiao^{1， 2}

1. State Key Laboratory of Nuclear Resources and Environment， East China University of Technology， Nanchang 330013， China

2. School of Geophysics and Measurement Control Technology， East China University of Technology， Nanchang 330013， China

Abstract： Analytic signal is a common tool for magnetic data processing and interpretation. Based on the relationship of different order analytic signals and their vertical derivative， this paper introduced a magnetic source variable depth imaging function with a depth scaled factor. The new method can be used for determining the position of filed source by using the maximum value of depth imaging， and estimating structural index on basis of the inverted depth and imaging maximum value. In addition， we can use the imaging results with different depth scaled factors and different orders to improve the reliability and usability of the new method. Model tests and applications indicate that the new method can    abtain  stronger computational  stability， higher spatial imaging resolution and more accurate field source parameter inversion results using lower-order derivatives， compared with the DEXP （depth from extreme points） methods of analytic signal ratio and local wavenumber.

Key words： magnetic source; analytic signal; depth imaging; structural index

0 引言

磁法勘探是金屬矿勘查最常用的地球物理方法之一，数据处理是磁测资料进行有效地质解释的关键环节^[1]。但受磁化方向影响，磁异常往往与地质体没有明显的对应关系，直接进行异常解释难度较大^[2]。常用的化极处理虽然可以将感应斜磁化磁异常转换成垂直磁化磁异常，在一定程度上有助于异常解释与推断^[3]，但当存在与感磁方向不一致的剩磁时，磁异常较复杂，化极很难获得满意效果^[4]。由于二维解析信号不受磁化方向影响，三维解析信号受磁化方向影响较小，因此解析信号成为磁法数据处理与解释的一种常用方法^[5-8]。

2003年，Salem等^[9]基于磁异常垂向导数解析信号和欧拉反褶积关系，提出了可以估计场源深度和构造指数的解析信号欧拉法；2005年，Salem^[10]又在解析信号导数基础上构建了线性方程组来估计场源位置；2012年，Ma等^[11]在2阶与1阶解析信号比值基础上完成了磁源深度及构造指数的估计；2014、2015年，Cooper^[12-13]也联合不同阶次解析信号确定了岩脉及台阶深度；2016年，Cooper等^[14]同样在不同阶次解析信号基础上提出了一系列场源参数估计方法；2017年，Cooper^[15]在解析信号对数的导数基础上实现了场源深度估计；2019年，Wang等^[16]在解析信号倒数的导数基础上构建了场源参数反演方程组；2021年，Wang等^[17]推导出了磁异常多阶解析信号的表达式，并在此基础上构建了线性反演方程组，用于估计磁源参数；2023年，王万银等^[18]分析了多种重磁场源深度反演方法的应用效果，并给出了不同方法的使用建议。上述方法均通过构建基于解析信号的磁源参数估计方程组获取场源深度和构造指数，但这类方法由于使用了磁异常不同阶次的导数，因此易受噪声干扰影响，往往需要事先进行向上延拓处理。

2013年，马国庆等^[19]利用解析信号相关成像识别场源空间位置并试算场源构造指数；2021年，马国庆等^[20]又采用解析信号导数与解析信号比值的相关成像来获取场源位置；2014年，Abbas等^[21]提出了解析信号比值的DEXP（depth from extreme points）方法实现磁源位置及构造指数估计；2018年，王彦国等^[22]利用幂次平均的离散归一化解析信号完成了场源快速成像；2022年，林涛等^[23]提出了层状位场及其梯度数据联合的相关成像法，提高了相关成像的纵、横向分辨率。这类方法是基于解析信号的场源快速成像，主要利用各自方法成像图中的极大值确定场源位置，但在一定程度上易受叠加异常或噪声干扰的影响。

本文在前人研究的基础上，基于不同阶解析信号及其垂向导数关系式，提出了一种新的场源快速成像方法，即磁源变深度成像法。该方法利用成像图中的极大值识别场源位置，利用成像极大值及深度估算场源构造指数。通过模型试验和应用实例验证本文方法的可行性、有效性及实用性，并與解析信号比值和局部波数的DEXP方法进行对比分析。

1 理论基础

二维磁异常T的1阶解析信号^[5]可表示为

式中，?T/?x及?T/?z分别为磁异常的1阶水平及垂向导数。S_a1与场源位置的关系^[9]可描述为

式中：k为与磁化强度有关的参数；（x， z）为观测位置；（x₀， z₀）为场源位置；N为构造指数，与地质体几何形状有关，N=0、1、2、3分别对应台阶、岩脉、圆柱体及球体。Ma等^[11]给出了2阶解析信号的表达式：

Wang等^[17]推导出了n阶解析信号表达式：

n阶解析信号的垂向导数可表示为

基于n阶解析信号垂向导数及n和n+1阶解析信号表达式，引入深度缩放因子β，定义磁源变深度成像函数为

式（6）对x、z进行求导，并令其等于0，则有：

求解式（7），得

x=x₀，z=βz₀/（β-0.5）。    （8）

由于向上延拓高度z≤0，因此0＜β＜0.5。当0＜β＜0.25时，相当于深度轴进行了压缩；当β=0.25时，深度轴无缩放；而当0.25＜β＜0.50时，深度轴进行了放大。由式（8）可知，在坐标点（x₀， ββ-0.5z₀）处，函数I^β_n存在极大值（易证明，此处略），因此可以利用函数I^β_n极大值估计场源位置。

当场源位置确定后，可以利用式（6）计算场源的构造指数：

虽然该方法使用了高阶导数，但同样使用了稳定的向上延拓处理，因此计算结果具有一定的稳定性。另外，当选择较小的β时，结果具有较高的空间成像分辨率及较高的计算精度，但更易受噪声干扰影响；当选择较大的β时，结果具有较强的稳定性，空间成像分辨率却较低。一般情况下，对于深部场源或者叠加场而言，建议选择较小的β值；而对于浅部磁源，且当数据信噪比较低时，可选择较大的β值。

为便于使用本文提出的磁源变深度成像方法，给出了该方法的主要计算流程。

1）选择β值，给定向上延拓高度间隔Δz，则缩放后的高度间隔为βΔz/（0.5-β）。

3）计算磁源变深度成像函数，并对深度轴按（0.5-β）/β比例进行回放，然后根据成像极大值确定场源空间位置。受异常叠加或噪声干扰影响，成像结果中可能包含虚假信息，不过这些虚假信息表现为偶极特征（同一水平位置，邻近深度上存在极大值与极小值），因此极易被识别出。

4）根据成像极大值及深度，利用式（9）计算场源构造指数。

2 模型试验

2.1 单一模型

为了测试本文方法的可行性与有效性，首先进行单一模型试验。该模型是一个上顶埋深为1 km、宽度为0.1 km的岩脉、磁化强度为10 A/m、有效磁化倾角为45°。图1给出了该岩脉在地面产生的理论磁异常及含10%噪声的异常，其中计算点距为0.1 km。

图2是无噪声时β=0.10、 0.25、 0.35，Δz=0.1 km时的1、2阶深度成像结果，可以看出：所有成像结果中仅存在一个极大值，均位于（5 km， 1 km）处，与岩脉的上顶位置完全一致；不过β=0.10时的成像结果更加聚焦，而β=0.35时的成像结果较为发散。I^0.1₁（图2a）、I^0.1₂（图2b）、I^0.25₁（图2c）、I^0.25₂（图2d）、I^0.35₁（图2e）及I^0.35₂（图2f）的极大值分别为1.098 7 km^-0.4、1.343 8 km^-0.4、1.000 2 km^-0.25、1.222 8 km^-0.25、1.039 3 km^-0.15及1.276 6 km^-0.15，利用式（9）计算得到的构造指数分别为0.99、0.98、1.00、0.99、0.99和1.00，同样与岩脉的理论构造指数1一致。

图3是磁异常含10%噪声时不同深度缩放因子条件下的深度成像结果，可以看出：噪声干扰虽然全部限制在近地表，但I^0.25₁（图3a）反映的极大值位于（5 km， 0.2 km）处，与场源真实位置存在显著偏差，而I^0.25₂（图3b）无有效极大值；当β增大至0.35时，成像结果具有较强的稳定性，1、2阶成像图的有效极大值均位于（5 km， 0.9 km）处，与场源真实位置较吻合（图3c、d）。根据极大值数据及场源位置，本文方法计算得到的构造指数分别为0.92及0.90，同样与理论构造指数较为接近。

该单一模型实验表明了新方法在场源成像及构造指数估计方面具有可行性，同时利用不同的深度缩放因子可提高方法的有效性及适用性。

为了体现方法的优越性，选择与本文方法原理相近的DEXP方法进行对比分析，图4给出了含10%噪声时单一模型磁异常解析信号比值DEXP和局部波数DEXP的成像结果。可以看出：无论是2阶与1阶、3阶与2阶解析信号比值的DEXP，还是1、2阶局部波数的DEXP，均无法有效反映出场源位置。这表明DEXP方法虽然使用了向上延拓，但仍会在强噪声干扰环境下失效。

2.2 叠加模型

为了测试本文方法在叠加异常上的应用效果，建立了由1个台阶、2个岩脉和2个圆柱体构成的叠加模型，选取的测线长度为600 m，点距为1 m。台阶水平位置为100 m，上顶埋深为25 m，磁化强度为0.01 A/m，有效磁化倾角为60°；两个岩脉分别位于200、300 m处，上顶埋深分别为15和20 m，磁化强度均为1 A/m，磁化倾角分别为45°和60°；两个水平圆柱体半径均为5 m，质心分别处于（400 m， 30 m）和（500 m， 35 m），磁化强度均为1 A/m，磁化倾角分别为45°和60°。图5a是该叠加模型在地表上产生的磁异常，包含了1%的随机噪声。图5b是图5a含噪声磁异常的1、2阶解析信号，可以看出：1阶解析信号存在5个明显的极大值，分别对应着5个模型体水平位置，但受噪声干扰影响，异常稳定性较差；2阶解析信号受噪声影响明显，已经无法反映出有效信息。

图6是叠加模型不同深度缩放因子1、2阶磁源深度成像的结果，其中Δz=1 m。可以看出：β=0.10时1阶深度成像结果（图6a）仅在（99 m，28 m）和（198 m， 18 m）处存在极大值，极大值分别为0.225 9 m^-0.4、0.397 6 m^-0.4，对应的构造指数分别为0.21和1.63， 这两个极大值分别对应台阶和第一个岩脉，但深度估计值及构造指数均大于真实值；β=0.10的2阶深度成像结果（图6b）可以反映出所有模型体的位置，5个极大值分别位于（99 m， 25 m）、（199 m， 17 m）、（300 m， 23 m）、（399 m， 32 m）和（499 m， 37 m），极大值分别为0.302 6 m^-0.4、0.458 5 m^-0.4、0.411 2 m^-0.4、0.401 4 m^-0.4和0.374 4 m^-0.4，构造指数分别为-0.02、1.35、1.43、2.25和2.15，估计得到的场源参数值与理论值较为接近，存在的误差主要是由叠加异常引起的；β=0.15时的2阶深度成像结果（图6c）同样存在5个极大值，分别处于（99 m， 27 m）、（199 m， 17 m）、（300 m， 29 m）、（399 m， 36 m）和（499 m， 40 m），極大值分别为0.338 1 m^-0.35、0.500 5 m^-0.35、0.457 3 m^-0.35、0.453 4 m^-0.35和0.425 4 m^-0.35，估计的构造指数分别为0.11、1.35、2.07、2.65和2.41，相对于图6b而言，虽其浅部存在的噪声干扰更加不敏感，但场源参数估计值与真实值偏差却更大。也就是说，对于叠加场，在阶次一样的情况下，深度缩放因子越大，深度成像稳定性越好，但精度越低。

图7是叠加模型解析信号比值DEXP的成像结果：2阶与1阶、3阶与2阶解析信号比值的DEXP均不能识别出任意场源的位置；4阶与3阶解析信号比值的DEXP也仅有2个极大值，位于（94 m， 25 m）和（199 m， 15 m），极大值分别为0.293 3 m^-0.5和0.515 9 m^-0.5，计算的构造指数分别为-0.07和1.00，估计的场源参数值与台阶和第一个岩脉参数值较为吻合。

图8是叠加模型局部波数DEXP的成像结果：1阶局部波数DEXP可以在（103 m， 26 m）处识别出台阶位置，极大值为0.116 5 m^-0.5，构造指数为0.19，但无法识别出余下4个场源；2阶局部波数DEXP无法识别出任意模型体位置；3阶局部波数DEXP存在2个有效极大值，位于（96 m， 27 m）和（199 m， 15 m），极大值分别为0.291 2 m^-0.5和0.515 9 m^-0.5，构造指数分别为0.03和1.00，较好地估计出了台阶和第一个圆柱体的位置及构造指数，但同样不能反映出其他3个模型体。

对比图6与图7和图8可以看出，本文方法具有更强的场源参数估计能力，能够较好地反演出所有模型体的位置并估计出构造指数。而且，本文中的2阶磁源变深度成像相当于使用了磁异常的3阶导数，但解析信号比值及局部波数的DEXP即使使用了4阶导数，也不能反映出所有场源信息。

3 实例应用

为了测试本文方法对实际资料的应用效果，选取黑龙江嫩北农场青年点地区1∶1万地面高精度磁测数据进行测试。测区地表全部被第四系沉积层所覆盖，下部主要是无（弱）磁性的二长花岗岩，但钻探结果表明临近该研究区的科洛金矿、三合屯金矿等矿床地下存在着中强磁性的闪长（玢）岩脉和褐铁矿化蚀变带，且与金矿体分布有着密切关系^[24-27]。图9是点距为20 m的地面磁异常，可以看出，磁异常场中包含了数十条条带状磁异常，其中中部存在的两条近南北向条带异常最为明显，已被槽探工作证实为褐铁矿化蚀变带。选取图9中AA剖面进行磁源深度成像方法的测试，并与解析信号比值及局部波数的DEXP方法进行对比分析。图10a是AA剖面的磁异常，图10b是1阶解析信号，可以看出，解析信号中包含了5个较为明显的极大值，分别位于100，340，760，1 320和2 560 m处。

图11是AA剖面β=0.1、0.2，Δz=5 m的1、2阶磁源深度成像结果。由图11可见，除了β=0.1的2阶磁源深度成像不能识别340 m处磁异常对应的磁源外，其他3幅成像图均清晰地展示出了5个有效的极大值，其对应场源位置、极大值及估算的构造指数见表1，可以看出不同深度缩放因子、不同阶次的磁源深度成像结果得到的场源参数基本一致。如果所有磁源深度成像结果进行平均的话，那么场源1—5分别位于（100 m， 41 m）、（340 m， 42 m）、（760 m， 46 m）、（1 320 m， 45 m）和（2 570 m，43 m）处，构造指数分别为1.09、1.52、1.91、1.20和1.05。构造指数估计值表明场源1、4、5接近于典型的岩脉，而场源2、3则具有一定的宽度。

图12是AA剖面解析信号比值DEXP的成像结果，结果显示，只有2阶与1阶解析信号比值的DEXP可以有效识别出3个极大值，而3阶与2阶、4阶与3阶解析信号比值的DEXP只能有效识别出2个极大值。极大值对应的场源1、4、5位于（87 m， 35 m）、（1 320 m， 43 m）和（2 580 m， 35 m）处，构造指数分别为0.94、1.07和0.98，表明这3个场源均是岩脉状的。

图13是AA剖面局部波数DEXP的成像结果，1、2、3阶局部波数的DEXP均有效地识别出了4个极大值，对应场源1、3、4、5，分别位于（100 m， 35 m）、（760 m， 40 m）、（1 320 m， 42 m）和（2 573 m，40 m）处，构造指数分别为0.91、1.72、1.02和0.96，即显示场源1、4、5接近于岩脉，而场源3具有一定的宽度。

对比图11与图12、图13可以看出，本文提出的磁源深度成像方法能够识别出5个场源位置，而解析信号比值、局部波数的DEXP方法均不能识别出所有场源位置；另外，本文方法提供的4个反演结果可相互对比来进一步提高结果的可靠性。

4 结论

1）本文在多阶次解析信号基础上提出了一种新的磁源变深度成像方法，该方法无需先验信息，可以快速地反映场源空间位置及估计构造指数。

2）由于新方法引入了可灵活选择的深度缩放因子，因此方法具有较强的灵活性，还可以结合不同深度缩放因子的成像结果来提高反演结果的可靠性。另外，由于使用了稳定的向上延拓，方法可直接使用，无需进行滤噪处理。

3）模型试验表明，相对于解析信号比值和局部波数的DEXP方法，本文方法不仅适用于强干扰情况，而且更加适合于复杂叠加异常的处理，反演得到的场源参数值也更加接近真实值；另外本文方法使用的导数阶次更低些。

4）实例应用中选取的磁测剖面成像结果表明，解析信号比值、局部波数的DEXP識别出的磁源数少于本文磁源变深度成像识别出的磁源数，且本文方法提供了4个不同的场源成像结果，使得本方法计算结果更加可靠。

参考文献（References）：

[1]赵东东，王旭龙，周印明，等. 基于泊松方程的空间波数混合域二度体磁异常数值模拟[J]. 吉林大学学报（地球科学版），2022，52（2）： 592-601.

Zhao Dongdong， Wang Xulong， Zhou Yinming， et al. Two-Dimensional Numberical Modeling of Magnetic Anomalies Based on Poisson Equation in Space-Wavenumber Mixed Domain[J]. Journal of Jilin University （Earth Science Edition）， 2022， 52（2）： 592-601.

[2]王彦国，邓居智，葛坤朋，等. 基于重磁泊松定理的磁化方向估计及应用：以相山铀矿田为例[J]. 地球物理学报，2022， 65（12）： 4914-4929.

Wang Yanguo， Deng Juzhi， Ge Kunpeng， et al. Estimating Magnetization Direction of Filed Sources Based on Poissons Theorem of Gravity and Magnetic Anomaly and Its Application： A Case of Xiangshan Uranium Orefield [J]. Chinese Journal of Geophysics， 2022， 65（12）： 4914-4929.

[3]羅潇，王彦国，葛坤朋，等. 基于方向tilt-Euler的三维磁数据快速反演[J]. 地球物理学报，2021， 64（6）： 2127-2140.

Luo Xiao， Wang Yanguo， Ge Kunpeng， et al. Fast Inversion of 3D Magnetic Data Based on the Directional Tilt-Euler Method [J]. Chinese Journal of Geophysics， 2021， 64（6）： 2127-2140.

[4]王妙月，底青云，许琨，等. 磁化强度矢量反演方程及二维模型正反演研究[J]. 地球物理学报，2004， 47（3）： 528-534.

Wang Miaoyue， Di Qingyun， Xu Kun， et al. Magnetization Vector Inversion Equations and 2D Forward and Inversed Model Study [J]. Chinese Journal of Geophysics， 2004， 47（3）： 528-534.

[5]Nabighian M N. The Analytic Signal of Two-Dimensional Magnetic Bodies with Polygonal Cross-Section： Its Properties and Use for Automated Anomaly Interpretation [J]. Geophysics， 1972， 37： 507-517.

[6]Roest W R， Verhoef J， Pikington M. Magnetic Interpretation Using the 3-D Analytic Signal [J]. Geophysics， 1992， 57（1）： 116-125.

[7]Aydin I. Estimation of the Location and Depth Parameters of 2D Magnetic Sources Using Analytical Signals [J]. Journal of Geophysical and Engineering， 2008， 5： 281-289.

[8]Zhou S， Huang D N， Su C. Magnetic Anomaly Depth and Structural Index Estimation Using Different Height Analytic Signals Data [J]. Journal of Applied Geophysics， 2016， 132： 146-151.

[9]Salem A， Ravat D. A Combined Analytic Signal and Euler Method （AN-EUL） for Automatic Interpretation of Magnetic Data [J]. Geophysics， 2003， 68（6）： 1952-1961.

[10]Salem A. Interpretation of Magnetic Data Using Analytic Signal Derivatives [J]. Geophysical Prospecting， 2005， 53（1）： 75-82.

[11]Ma G Q， Du X J. An Improved Analytic Signal Technique for the Depth and Structural Index from 2D Magnetic Anomaly Data [J]. Pure and Applied Geophysics， 2012， 169： 2193-2200.

[12]Cooper G R J. The Automatic Determination of the Location and Depth of Contacts and Dykes from Aeromagnetic Data [J]. Pure and Applied Geophysics， 2014， 171： 2417-2423.

[13]Cooper G R J. Using the Analytic Signal Amplitude to Determine the Location and Depth of Thin Dykes from Magnetic Data [J]. Geophysics， 2015， 80（1）： J1-J6.

[14]Cooper G R J， Whitehead R C. Determining the Distance to Magnetic Source [J]. Geophysics， 2016， 81： J25-J34.

[15]Cooper G R J. Determining the Depth and Location of Potential Field Sources Without Specifying the Structural Index [J]. Arabian Journal of Geoscience， 2017， 10： 1-7.

[16]Wang Y G， Luo X， Zhang J. Interpretation of 2D Magnetic Sources Based on the Reciprocal of the Analytic Signal Amplitude [J]. Exploration Geophysics， 2019， 50： 645-652.

[17]Wang Y G， Ding Y Z， Ai H B. Estimation of 2D Magnetic-Source Parameters Using Analytic Signals of the Logarithm of Different Order Analytic Signals [J]. Exploration Geophysics， 2021， 53（3）： 314-328.

[18]王萬银，罗新刚. 重磁场二度体边缘深度反演研究进展[J]. 物探与化探，2023， 47（3）： 547-562.

Wang Wanyin， Luo Xingang. Research on Edge Depth Inversion of 2D Geological Body Based on Gravity and Magnetic Field [J]. Geophysical and Geochemical Exploration， 2023， 47（3）： 547-562.

[19]马国庆，杜晓娟，李丽丽. 改进的位场相关成像方法[J]. 地球科学：中国地质大学学报，2013， 38（5）： 1121-1127.

Ma Guoqing， Du Xiaojuan， Li Lili. Improved Potential Field Correlation Imaging Method [J]. Earth Science：Journal of China University of Geosciences， 2013， 38（5）： 1121-1127.

[20]马国庆，牛润馨，李丽丽，等. 基于重磁不同阶比值的场源相关成像法研究[J]. 地球物理学进展，2021， 36（5）： 2062-2068.

Ma Guoqing， Niu Runxin， Li Lili， et al. Non-Degree Gradient Ratio Function of Gravity and Magnetic Data for Field-Source Correlation Imaging Method Study [J]. Progress in Geophysics， 2021， 36（5）： 2062-2068.

[21]Abbas M A， Fedi M. Automatic DEXP Imaging of Potential Fields Independent of Structural Index [J]. Geophysical Journal International， 2014， 199： 1625-1632.

[22]王彦国，吴姿颖，邓居智，等. 基于幂次平均的离散归一化总梯度法[J]. 石油地球物理勘探，2018， 53（6）： 1351-1364.

Wang Yanguo， Wu Ziying， Deng Juzhi， et al. Discretization of Normalized Total Gradient Based on Power Mean [J]. Oil Geophysical Prospecting， 2018， 53（6）： 1351-1364.

[23]林涛，曾昭发，于平，等. 基于层源位场的重力及其梯度数据联合相关成像[J]. 世界地质， 2022， 41（1）： 186-197.

Lin Tao， Zeng Zhaofa， Yu Ping， et al. Joint Probability Tomography for Gravity and Its Gradiometry Data Based on Strata-Source Potential Field [J]. World Geology， 2022， 41（1）： 186-197.

[24]李成禄. 黑龙江省嫩江—黑河构造混杂岩带金矿成矿作用及找矿预测[D]. 北京：中国地质大学（北京），2018.

Li Chenglu. Gold Metallogeny and Prospecting in the Nenjiang-Heihe Tectonic Mélange Zone， Heilongjiang Province [D]. Beijing： China University of Geosciences（Beijing）， 2018.

[25]赵忠海. 小兴安岭西北部永新大型金矿成因、成矿地质模型与深部三维成矿预测[D]. 长春：吉林大学，2019.

Zhao Zhonghai. Ore Genesis， Metallogenic Geological Mode and Deep Metallogenic Prediction of the Yongxin Large Au Deposit Based on 3D Digital Model in the Northwestern Lesser Xingan Range [D]. Changchun： Jilin University， 2019.

[26]刘宝山，程招勋，邵军，等. 黑龙江嫩江—黑河地区铜金多金属找矿新进展及勘查方向[J]. 地质与资源，2022， 31（3）： 331-341.

Liu Baoshan， Cheng Zhaoxun， Shao Jun， et al. Latest Prospecting Progress and Exploration Direction of Copper-Gold Polymetallic Deposits in Nenjiang-Heihe Area， Heilongjiang Province [J]. Geology and Resources， 2022， 31（3）： 331-341.

[27]李博文，谷华娟，李成禄，等. 黑龙江省三合屯金矿床地质特征及找矿潜力分析[J]. 黄金科学技术，2022， 30（4）： 508-517.

Li Bowen， Gu Huajuan， Li Chenglu， et la. Geological Characteristics and Prospecting Potential of Sanhetun Gold Deposit in Heilongjiang Province [J]. Gold Science and Technology， 2022， 30（4）： 508-517.