基于建模数据和最优化算法的GaN HEMT精确电热行为建模方法

肖 龙（中国电源学会会员），陈冬冬

（闽南理工学院电子与电气工程学院，泉州 362700）

氮化镓高电子迁移率晶体管GaN HEMT（gallium nitride high electron mobility transistor）作为可控型宽禁带功率半导体器件的典型代表，能够在提高耐压等级的同时减小导通电阻，具有比同等耐压等级的硅基功率半导体器件更小的导通电阻和更快的开关速度，因此在高频和高功率变换器中得到越来越广泛的应用[1-5]。然而，由于寄生参数的存在，GaN HEMT 高速的开关带来了严重的电压应力[6]、串扰导通[7]、门极谐振[8]、开关振荡和EMI 噪声[9]等问题。因此，迫切需要GaN HEMT 精确的行为仿真模型，用于分析和解决高速开关带来的上述问题，并用于实现高频和高功率密度功率变换器的仿真和优化设计[10-12]。

当前，国内外学者围绕宽禁带器件建模展开了大量的研究[11-28]。和国外相比，国内关于宽禁带器件建模的研究主要集中在碳化硅场效应晶体管上[19-21]，关于GaN HEMT 器件建模的研究则主要集中在GaN HEMT 微波器件和GaN HEMT 电力电子器件的高效应用方面[22-25]，而关于GaN HEMT 功率器件行为模型的研究则较少。根据文献[11]，GaN HEMT仿真模型主要可以分为物理模型和经验模型2 种。其中，基于表面势理论和基于电荷理论的物理模型的建立依赖于具体的器件制造参数，不仅建模困难而且计算工作量大，因此不适合用于变换器的电路仿真[13-16]。相比之下，建模简单且具有足够精确度的GaN HEMT 行为仿真模型更加受到青睐。文献[12]采用分段连续的函数对GaN HEMT 在第一和第三工作象限的静态输出特性展开建模。尽管模型在第三象限的准确性较高，但是模型在第一象限的仿真结果却和实验结果存在较大的偏差。通过对砷化镓金属半导体场效应晶体管模型的改进，文献[17]提出一种用于GaN HEMT 仿真的非线性经验模型，但是所提出的经验模型没有对GaN HEMT 的第三工作象限展开建模，同时没有考虑温度对模型参数的影响，因此不适用于电热行为特性的仿真。文献[18]通过改进Pspice 中内置的MOSFET 模型对GaN HEMT 的静态特性展开建模，然而其仅在室温下对所提模型的输出特性准确性进行验证，同时也没有对GaN HEMT 第三象限的特性进行建模，此外没有对模型的动态开关特性展开验证。除了上文介绍的2 种仿真模型外，还存在一种用于电力电子变换器分析的解析模型[26，28]。虽然解析模型有利于开展GaN HEMT 动态开关过程、开关过程应力、串扰和振荡问题的研究，但是解析模型建立在简化的经验模型的基础上，往往忽略了器件寄生参数的非线性特性。因此解析模型准确性一般都低于经验公式模型，一般仅适用于开展定性的分析。

综合以上分析可以看出，目前现有的GaN HEMT 经验模型存在模型准确度低，不能开展电热行为仿真，不能对第三象限展开准确建模和模型参数提取困难等不足。针对这一问题，本文提出一种GaN HEMT 精确电热行为模型建模方法。首先提出紧凑的建模公式对GaN HEMT 在第一和第三象限的电热输出特性及非线性寄生电容展开建模。接着，提出一种遗传算法GA（genetic algorithm）和L-M（Levenberg-Marquardt）算法结合的复合优化算法，并基于建模数据，实现建模参数的自动化提取，大大简化模型参数提取的时间和工作量。最后对所提出的电热行为模型的动静态电热特性展开仿真和实验研究，验证所提模型的正确性和有效性。

1 GaN HEMT 电热行为模型

本文建立的GaN HEMT 电热行为仿真模型的子电路结构如图1 所示。

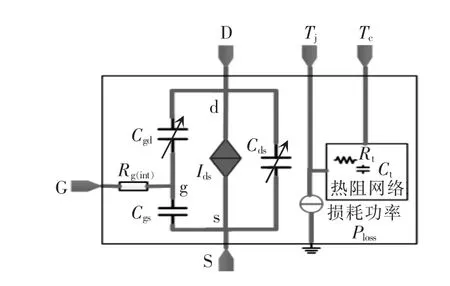
图1 GaN HEMT 电热行为模型子电路结构Fig.1 Structure of subcircuit of GaN HEMT electrothermal behavior model

其中，GaN HEMT 的静态电热行为特性由受控电流源Ids进行建模；Cgs、Cgd和Cds分别为GaN HEMT 的寄生电容；Rg（int）为门级内部电阻；引脚D、G 和S 分别为行为模型连接外部器件的漏极、门极和源极端口。由于门级增强型GaN HEMT 的体积和封装尺寸均比较小，这里忽略了器件封装带来的寄生电感。模型中采用热等效电路对GaN HEMT的热特性进行建模。通过实时计算仿真过程中的漏源电压和沟道电流的乘积可以获得损耗功率Ploss。采用受控电流源对损耗功率进行建模，模型的结温引脚Tj和损耗功率源直接连接，模型的壳温引脚Tc通过由热阻Rt和热容Ct组成的器件内部封装构成的热阻抗网络连接到功率损耗源。其中，内部封装热阻抗网络模型可以从器件的仿真模型获得，也可以从器件数据手册中获得器件等效的热阻和热容。通过设置模型的结温引脚Tj和壳温引脚Tc所连接的外加热源和热阻抗网络，可以对任意散热条件下GaN HEMT 器件的结温和壳温展开准确的仿真。

通过对文献[29]所提出的建模公式进行改进，本文提出的受控电流源Ids的经验建模公式为

式中：Vth为门槛电压，根据文献[30]，GaN HEMT 的门槛电压基本不随温度而漂移，因此采用恒定值对门槛电压进行建模；Vgs为门极电压；Vds为漏源电压；gm为等效跨导，它是结温Tj的函数，用于对GaN HEMT 输出特性随温度的变化进行建模；θ 为载流子迁移率退化系数，它是门极电压的函数，θ的提出是考虑到沟道载流子迁移率会随着门极电压产生的垂直电场造成的载流子迁移率的降低；β、h（Vds）均为漏源电压的函数，以实现对沟道电流随漏源电压的变化特性展开建模。

式中，a0～a9为模型参数，下文将基于所提出的优化算法和建模数据实现参数a0～a9的一次性快速提取。通过对GaN HEMT 第一象限的建模公式进行改进，对GaN HEMT 在第三工作象限的特性进行建模，即

式中：Vgd为栅漏电压；b0～b7为建模参数，其提取方法将在第2 节详细介绍；和第一象限的相似，θ' 为载流子迁移率退化系数，是栅漏电压的二次多项式函数。

对于GaN HEMT 器件的非线性寄生电容，将采用文献[3]中的建模公式进行准确建模。

式中：Ci（i=gs，gd 和ds）为GaN HEMT 的3 个寄生电容；k0_i～k4_i（i=gs，gd 和ds）为相应非线性电容模型的参数，这些参数的提取方法将在下文详细给出。

2 模型参数提取

从上文分析可以看出，所建立的GaN HEMT的电热行为模型中包含了大量的模型参数。如果采用传统的分段拟合的方法来实现模型参数的提取，不仅增加了建模的时间和工作量，同时无法保证模型参数的全局最优，也无法实现建模公式的快速筛选与迭代设计。为了解决这一问题，本节首先提出一种GA 和L-M 结合的复合优化算法，借此实现基于建模数据和优化算法的模型参数快速提取；接着以GaN Systems 公司的GaN HEMT GS61008p 为例，给出模型参数提取的详细过程。

2.1 GA 和L-M 复合优化算法

L-M 算法是非线性最小二乘法的典型代表，广泛用于非线性模型的参数拟合。在合适的初值条件下，L-M 算法能够在若干步迭代后快速收敛到局部最优值，是一种非常高效的局部优化算法。然而，当选取的初值不合理时，L-M 算法不仅收敛速度变慢，而且无法收敛到全局最优解，甚至出现无法收敛的现象[31-33]。如果拟合公式的待拟合参数过多，通过试凑法来设定拟合参数初始值的工作量将非常大，显然不是一种可取的办法。因此单独使用L-M算法难以实现模型参数的快速提取，也不利于实现经验公式的快速迭代设计。

GA 算法是一种全局优化算法，而且可以通过设置GA 算法参数取值的上限UB（upper bound）和下限LB（lower bound）来加快算法的收敛速度。然而，GA 算法在局部优值附近的收敛速度却比较慢。因此，GA 算法非常适合用于复杂模型参数的初步选取。基于以上分析，本文提出一种结合GA 和L-M算法各自优点的复合优化算法。首先采用GA 算法实现模型参数的初步确定，然后将GA 算法确定的初始拟合参数传递到L-M 算法中，实现模型参数的快速提取。所提优化算法的执行流程如图2 所示。

图2 GA 和L-M 复合优化算法流程Fig.2 Flow chart of GA and L-M combined optimization algorithm

图2 中，采用静态电热输出电流Ids的建模公式（1）作为实例展示复合优化算法的实现过程。在GA 算法中，参数a0～a9是待拟合的建模参数，这些参数的取值范围在各自的取值范围[LBi，UBi]（i=0～9）内。GA 算法的适应度函数Fk是不同结温、门极电压和漏源电压下，漏源电流的测量值和估计值之差的平方和。经过遗传算法计算后，当适应度函数Fk小于预先设定的拟合误差εGA，或者遗传算法的步数达到预先设定的计算步数上限NGA后，遗传算法计算结束，输出遗传算法拟合得到的初步计算参数a0（GA）～a9（GA）到L-M 算法，作 为L-M 算 法的参数初值。

L-M 算法是一种带修正项的高斯-牛顿算法，其具体实现过程如图2 所示。和GA 算法一样，采用测量值和拟合值之差的平方和Gk与预设的拟合误差εLM作为判断L-M 算法收敛的判据。当L-M 算法计算误差小于预设误差，或L-M 算法的运行步数达到预设的最大运行次数NLM时，L-M 算法结束，输出最终拟合参数。

2.2 基于建模数据和优化算法的建模参数自动化

在2.1 节给出GA 和L-M 复合优化算法的基础上，本节以GaN Systems 公司生产的GaN HEMT GS61008P 为代表，展示基于所提出优化算法和建模数据的模型参数提取过程。

以式（1）～（5）所示的静态电热输出特性建模公式中的参数a0～a9的提取为例，首先需要获取建模所用的数据，这里直接从GS61008P 的数据手册中获取在结温Tj=25 ℃和Tj=150 ℃两种温度下，GS61008P 的转移特性曲线和输出特性曲线数据。接着将提取的全部建模数据代入所提出的GA 和L-M 复合优化算法中，实现模型参数a0～a9的一次性快速提取。

实际参数提取过程表明，在提取建模公式（1）～（5）中的参数a0～a9时，如果单独采用GA 算法实现，即使采用较大的种群数据经过较多次数的迭代优化，算法也很难收敛到局部最优值；而单独采用L-M算法时，算法几乎难以收敛。而当采用GA 和L-M 混合优化算法时，GA 算法只需要较少的种群数量并执行较少次的进化周期，即可输出令L-M 算法快速收敛的优化初值。通过将提取的电热输出特性建模数据代入复合优化算法中，在一台普通的笔记本电脑中，即可在10 s 内快速拟合出模型参数a0～a9，如表1所示。

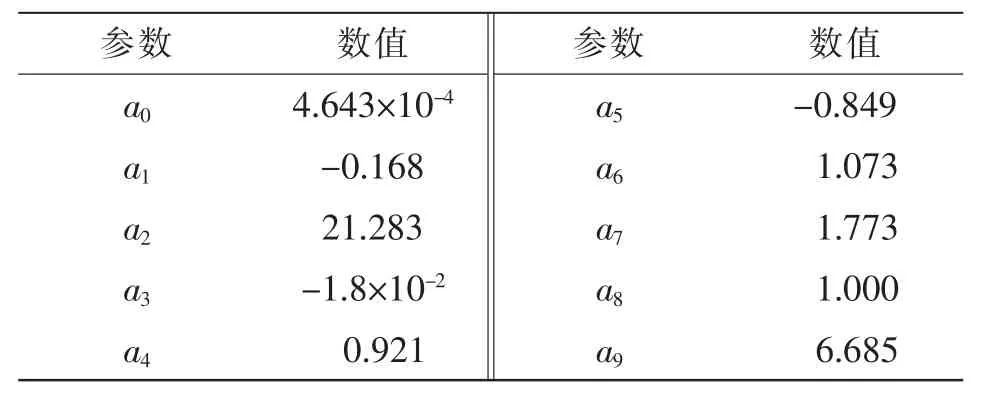
表1 GS61008P 第一象限输出特性模型参数Tab.1 Modeling parameters of GS61008P output characteristics in the first quadrant

采用同样的方法，通过从GS61008P 数据手册中获取的第三工作象限的数据，代入到建模式（7）和式（8）中，通过复合优化算法可以一次性提取出第三象限的模型参数，如表2 所示。

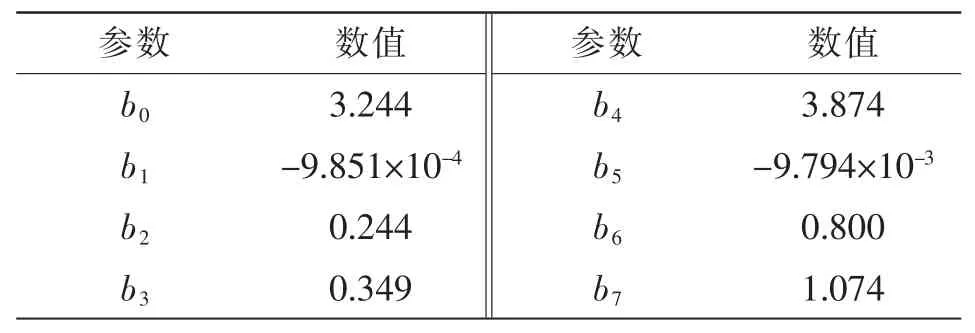
表2 GS61008P 第三象限输出特性模型参数Tab.2 Modeling parameters of GS61008P output characteristics in the third quadrant

GS61008P 的数据手册中给出了其输入电容Ciss、转移电容Crss和输出电容Coss随漏源电压的非线性变化曲线。根据式（9）可以计算出GS61008P三个非线性寄生电容Cgs、Cgd和Cds随漏源电压的变换曲线。

根据上式所获取的GS61008P 的非线性寄生电容建模数据，代入到建模公式（9）中，通过所提出的复合优化算法可以得到3 个非线性寄生电容的建模参数，如表3 所示。

表3 非线性寄生电容建模参数Tab.3 Modeling parameters of nonlinear parasitic capacitances

从上述参数提取建模过程可以看出，和以往建模方法中采用的根据特性曲线的局部数据实现建模参数的分段多步提取方法不同，所提的基于建模数据和优化算法的提取方法不仅能够实现参数的一次快速提取，而且能够实现建模参数的全局最优。这不仅能够缩小建模所用的时间和工作量，同时也有利于建模经验公式的快速迭代设计和建模过程的自动化。

3 仿真和实验验证

3.1 仿真验证

根据上文提出的建模公式和提取的模型参数，可以建立GS61008P 的SPICE 仿真模型，进而可以借助仿真模型验证所提出的建模方法和参数提取方法的正确性和有效性。图3 和图4 为根据所建立的GS61008P SPICE 仿真模型通过搭建相应的仿真电路，测量得到GS61008 的转移特性曲线、第一象限输出特性曲线、第三象限输出特性曲线和非线性寄生电容变化曲线。

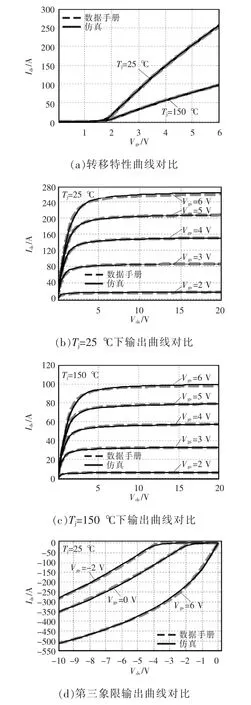
图3 转移特性曲线、第一和第三象限输出特性曲线Fig.3 Transfer characteristics curves,and output characteristics curves in the first and third quadrants

图4 GS61008P 非线性寄生电容的对比Fig.4 Comparison of nonlinear parasitic capacitances of GS61008P

通过图3 和图4 可以看出，仿真得到GS61008P的静态电热行为特性和数据手册给出的特性高度吻合，而且非线性寄生电容模型准确度也非常高。此外，采用所提出的建模方法对GaNSystems 公司的650 V 耐压的GaN HEMT GS66508B 和EPC 公司的GaN HEMT 半桥EPC2100 进行建模。图5 所示为采用所提出的建模方法对GS6650B 和EPC2100的输出特性进行建模的结果。

图5 GS66508B 和EPC2100 半桥的仿真和数据手册输出特性曲线的对比Fig.5 Comparison between simulated and datasheet extracted output characteristics curves of GS66508B and EPC2100 half-bridge

图3～图5 中，仿真和数据手册中的特性曲线均高度吻合，证明所提出的电热行为模型及其建模方法能够实现对多个公司不同型号的GaN HEMT电热行为特性的准确建模。

3.2 实验验证

为了进一步验证所提出的GaN HEMT 电热行为模型建模方法的正确性，本节采用双脉冲测试DPT（double pulse test）仿真和实验电路对GS61008P的动态开关特性展开对比研究。GaN HEMT 双脉冲电路的原理如图6 所示。

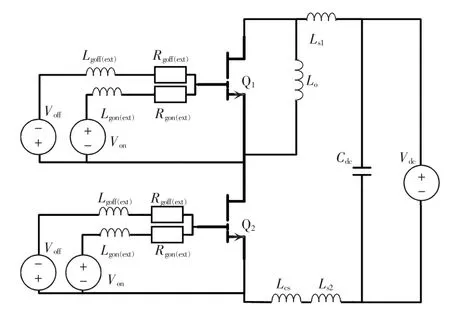
图6 GaN HEMT 双脉冲实验电路原理Fig.6 Schematic of DPT circuit for GaN HEMT

图6 中，Ls1、Ls2为主功率电路上的杂散电感，杂散电感值可以通过Ansys Q3D 进行提取。Lcs为同轴分流器引脚引入的寄生电感，Lo为双脉冲实验的负载电感。实验中分别采用驱动电压Von和Voff对GaN HEMT进行开通和关断，Lgon（ext）、Rgon（ext）分别为门极开通回路的杂散电感和开通电阻，Lgoff（ext）、Rgoff（ext）分别为门极关断回路的杂散电感和关断电阻。Q1、Q2分别为GaN HEMT 的上管和下管。双脉冲电路所有电路参数的数值如表4 所示。

表4 DPT 测试电路参数Tab.4 Parameters of DPT circuit

实验中上管Q1保持关闭状态，在下管Q2的门极施加双脉冲驱动信号，同时测量下管Q2的漏源电压和漏源电流。根据双脉冲实验电路原理搭建的双脉冲实验测试平台如图7 所示。

图7 双脉冲实验测试平台Fig.7 Testbench for DPT

根据文献[34]，测量仪器的带宽需要满足式（10）所示的带宽要求，而且需要对测量探头和测量通道间延时进行校准，以实现GaN HEMT 高速开关波形的准确测量。

式中，tr和tf分别为动态开关波形的上升时间和下降时间。本文中所采用的测量仪器及其相关参数如表5 所示。

表5 测量仪器及参数Tab.5 Measurement instruments and their parameters

根据所搭建的DPT 测试电路和所选用的测量仪器，测量GS61008P 在Tj=25 ℃下动态波形，如图8所示。

图8 仿真和实验得到的开关波形对比Fig.8 Comparison between simulated and measured switching waveforms

从图8（a）和图8（b）中可以看出，仿真和实验得到的漏源电压上升和下降速率基本相同。由于功率回路电感的存在且关断速度较快，GS61008P 在硬关断时存在较大的关断过冲振荡。仿真和实验测量得到的漏源电压关断过压峰值、谐振频率及振荡的衰减速度基本一致。由于采用阻值只有0.01 Ω的同轴分流器测量电流，所以电流测量信号比较微弱，容易受到外部干扰的影响，如图8（c）和图8（d）中测量的动态电流波形中出现了若干波动尖峰。但是总体上来说，仿真和实验测量得到的漏源电流动态波形基本重合。综合来说，仿真和实验测量得到的GS61008P 动态开关波形能够较好地吻合，证明了所提出GaN HEMT 电热行为模型建模方法的正确性。

4 结论

本文提出一种精确的门极增强型GaN HEMT电热行为模型建模方法。不仅给出了GaN HEMT在第一和第三工作象限的电热行为特性的准确建模公式，而且提出了一种基于GA 和L-M 复合优化算法和建模数据的建模参数快速提取方法。最后采用仿真和实验验证了本文所提出的GaN HEMT 电热行为特性建模方法的正确性和有效性。

基于本文提出的GaN HEMT 建模方法，不仅提高了GaN HEMT 电热行为模型的准确性，而且减小了建模的时间和工作量，为实现门极增强型GaN HEM 行为建模的自动化提供了可能。同时基于本文提出的建模方法实现的GaN HEMT SPICE模型的收敛性好，在基于GaN HEMT 器件的功率变换器的仿真和优化设计中具有一定的应用前景。