一种基于ISBO 算法的锂离子电池等效电路模型辨识方法研究
2024-02-26中国电源学会会员田海建
黄 凯(中国电源学会会员),田海建,丁 恒
(1.省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学),天津 300130;2.河北省电磁场与电器可靠性重点实验室(河北工业大学),天津 300130)
锂离子电池以其能量密度高、污染小及寿命长等优点被广泛应用于电动汽车、航空和航天等领域中[1-2]。建立精确的锂离子电池模型有利于更好地分析电池的荷电状态SOC(state-of-charge)和健康状态SOH(state-of-health)。常见的锂离子电池模型有电化学模型和等效电路模型[3]。电化学模型能够从机理层面描述电池的内部微观反应,但存在模型结构复杂、求解计算困难等缺点。等效电路模型利用电阻和电容等电学器件的组合来模拟电池的外特性,其结构简单直观且容易实现。因此目前等效电路模型在电池管理系统中应用广泛[4-7]。
模型参数辨识是建立等效电路模型过程中必不可少的步骤。参数辨识方法主要包括在线辨识和离线辨识。在线辨识方法利用电池实时测量的电压和电流等数据进行参数辨识,可以实现模型参数的在线更新,辨识精度较高,但对处理器的运行速度有较高的要求。离线参数辨识方法主要有最小二乘法和智能优化算法。与最小二乘法相比,智能优化算法对电池模型参数辨识精度较高,可靠性较强[8],目前已广泛应用于光伏电池和锂离子电池模型参数辨识过程。文献[9]采用一种基于混合教学的人工蜂群算法用于光伏电池模型参数辨识;文献[10]采用一种具有交叉率排序机制和动态种群减少策略的增强型自适应差分进化算法对光伏电池模型进行参数辨识;文献[11]采用一种基于自适应随机扰动的粒子群算法对锂离子电池模型进行参数辨识。缎蓝园丁鸟优化SBO(satin bowerbird optimization)算法是由Moosavi 等在2017 年提出的一种智能优化算法[12]。该算法融合了动态步长和变异操作,在步长变化的前提下更新种群的位置,同时在寻优后期个体的位置以一定的概率进行变异,有利于提高种群的多样性[13],但SBO 算法仍存在收敛精度低和收敛速度慢的缺点[14]。针对此问题,本文提出改进的缎蓝园丁鸟优化ISBO(improved satin bowerbird optimization)算法。在ISBO 算法中,通过引入惯性权重,增强算法的全局和局部搜索性能,同时采用柯西变异、高斯变异和贪婪选择策略来增加种群的多样性,提高算法的收敛效果。结合电池充放电数据,将ISBO 算法用于锂离子电池等效电路模型的参数辨识。
本文首先介绍SBO 算法原理,其次介绍ISBO算法原理并对其性能进行验证,然后给出等效电路模型原理及实验安排,接着采用ISBO 算法对电池模型进行参数辨识,再次分析实验结果并进行验证,最后对本文进行总结。
1 SBO 算法原理
雄性缎蓝园丁鸟通过构建巢穴吸引雌性园丁鸟。在构建巢穴的过程中,雄性缎蓝园丁鸟的巢穴可能会出现被其他雄鸟破环的现象。根据缎蓝园丁鸟的生活原理,SBO 算法主要包括以下6 个步骤。
(1)随机生成n 个园丁鸟的巢穴位置。
(2)计算每个园丁鸟个体的适应度Fi其在轮盘赌选择过程中被确定的概率Pi,表示为
式中,f(xi)为园丁鸟巢穴位置的目标函数。
(3)雄鸟通过与轮盘赌选择方法确定的个体和种群中最优个体之间的信息交流来更新巢穴的位置,其位置更新公式为
式中:i 为当前个体;j 为通过轮盘赌选择方法确定的个体;为第t 次迭代时第i 个个体的第d 维变量;为第t 次迭代时最优个体的第d 维变量;为第t+1 次迭代时第j 个个体的第d 维变量;λd为步长因子,计算公式为
式中:α 为步长上限;Pj为通过轮盘赌选择方法确定的第j 个个体的概率。
(4)强壮的雄鸟可能会破坏其他雄鸟的巢穴,巢穴的位置以一定的概率进行变异。位置变异公式为
式中:β 为标准差;N(0,1)为标准高斯分布产生的随机数。
(5)组合所有种群个体,并按目标函数值从小到大进行排序,保留函数值较小的个体,数量保持到原来种群的个数。
(6)判断是否满足终止条件。若满足,则输出最优位置及其对应的目标函数值;否则,执行步骤(2)。
2 ISBO 算法的提出及性能验证
传统SBO 算法存在收敛精度低的缺点,将其直接应用于锂离子电池参数辨识过程中,会导致模型出现精度不高的问题,因此提出ISBO 算法来提高电池模型的精度。
2.1 SBO 算法改进策略分析
2.1.1 引入惯性权重
由式(4)可知,传统SBO 算法主要是根据轮盘赌选择方法确定的个体的概率Pj进而来计算步长因子λd,该方法使得在每次迭代过程中园丁鸟的搜索步长没有明显规律,不利于提高算法的寻优效果。为了提高算法的全局和局部搜索能力,本文在SBO 算法的位置更新公式(3)中引入了惯性权重r。改进后的位置更新公式为
式中:t 为当前迭代次数;M 为最大迭代次数。经试验测试当r1和r2分别设置为0.9 和0.1 时,测试效果最佳。
由式(7)可知,随着迭代次数不断增加,惯性权重r 逐渐减小。在迭代初期,较大的惯性权重r 使得种群在较大的区域内进行搜索,有利于提高算法的全局搜索性能;在迭代后期,较小的惯性权重r使得种群在较小的区域内进行搜索,有利于提高算法的局部搜索性能。
2.1.2 融合柯西变异、高斯变异和贪婪选择策略
对个体进行变异操作有利于扩大个体搜索范围,提升算法的收敛精度。本文引入柯西变异和高斯变异来增加种群的多样性。柯西变异和高斯变异来源于柯西分布和高斯分布。标准柯西分布和高斯分布的概率密度函数表达式分别为
其函数图像如图1 所示。由图1 可知,标准柯西分布的概率密度函数在原点处分布较紧凑,而在两端分布较长,在原点处的峰值也比高斯分布小,所以柯西变异比高斯变异的扰动能力强。对个体进行柯西变异,使其能够在较大的范围内进行搜索,有利于提高种群的多样性,增强算法的寻优效果。因此,在每次更新的种群中,对目标函数值较差的后50%的个体进行柯西变异。经柯西变异后个体的位置表达式为
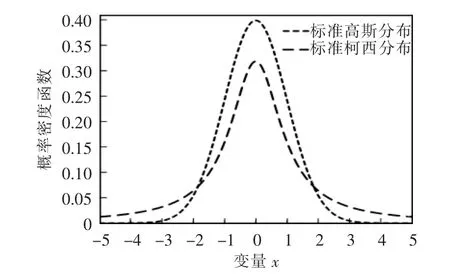
图1 标准柯西分布和高斯分布的概率密度函数Fig.1 Probability density functions of standard Cauchy distribution and standard Gaussian distribution
式中:x*为经柯西变异后个体的位置;cauchy(0,1)为标准柯西分布产生的随机数。
高斯变异具有良好的局部搜索能力,可以提升算法的寻优能力[15]。将种群中最优个体进行高斯变异,变异后个体的位置表达式为
式中,xN为经高斯变异后个体的位置。
为了提升算法的收敛精度,结合贪婪选择策略确定经柯西变异和高斯变异后个体的最终位置。贪婪选择策略是指变异后个体位置的目标函数值若优于原来位置的目标函数值,则将变异后个体的位置作为此次迭代过程中个体的最终位置,反之个体的位置将保持不变。贪婪选择策略的表达式为
式中:xr和xv分别为变异前和变异后个体的位置;xnew为采用贪婪选择策略后个体的最终位置。
2.2 ISBO 算法性能验证
2.2.1 柯西变异、高斯变异和贪婪选择策略对算法改进的有效性验证
为了定量分析柯西变异、高斯变异和贪婪选择策略对算法改进的有效性,利用6 个标准测试函数对ISBO 算法连续进行50 次实验测试。6 个标准测试函数的具体信息见表1。其中,f1~f4为单模态函数,f5、f6为多模态函数。每次实验过程中,算法的种群规模为20,迭代次数为100,标准测试函数的维数N 为20。表2 统计了50 次实验过程中经采取贪婪选择策略确定变异后个体最终位置的平均更新次数。

表1 标准测试函数Tab.1 Standard test functions

表2 位置更新次数Tab.2 Location update times
由表2 可以看出,对于标准测试函数f1~f4,经采用高斯变异和贪婪选择策略后个体的最终位置的平均更新次数在47 次左右,经采用柯西变异和贪婪选择策略后个体的最终位置的平均更新次数在389 次左右。说明在100 次迭代过程中,个体利用式(11)进行高斯变异产生100 个新位置,其中大约有47 个位置的目标函数值优于原来位置的目标函数值。同理,个体利用式(10)进行柯西变异产生1 000 个新位置,其中大约有389 个位置的目标函数值优于原来位置的目标函数值。由此说明,对个体进行柯西变异和高斯变异能够有效扰动个体原来的位置,变异后个体的位置能够优于原来位置。对于标准测试函数f5和f6,位置更新次数较多,说明经高斯变异和柯西变异后个体的位置大多数情况下优于原来位置。该实验结果同时验证了下文表5 中ISBO 算法对于标准测试函数f5和f6的收敛效果最为明显。标准测试函数f5和f6的收敛结果能够达到理论最优值0。综上分析,采用柯西变异、高斯变异和贪婪选择策略能够增加种群的多样性,提高算法的收敛精度。
2.2.2 ISBO 算法性能测试
为验证ISBO 算法性能,以2 维函数f(x,y)=x2+y2=0 为例,分析SBO 和ISBO 算法在100 次迭代过程中的最优位置。算法的种群规模为20。目标函数f(x,y)的理论最优点为(0,0)。SBO 和ISBO 算法在迭代过程中的最优位置见表3。

表3 不同迭代次数下的最优位置Tab.3 Optimal location under different iteration times
由表3 可知,SBO 算法在第50 次、第80 次和第100 次迭代过程中的最优位置并未发生变化。说明虽然迭代次数在不断增加,个体的位置发生变化,但种群中最优位置并未更新。ISBO 算法在迭代过程中的最优位置在发生变化且不断靠近理论最优位置(0,0),在第100 次迭代时,最优位置与理论最优位置(0,0)之间的距离远远小于SBO 算法。由此说明本文提出的ISBO 算法收敛精度明显高于SBO 算法。
为了验证ISBO 算法在高维空间中仍然具有较好的性能,采用表1 中的6 个标准测试函数分别对自适应权重粒子群优化AWPSO(adaptive weight par-ticle swarm optimization)算法[16]、SBO 和ISBO 算法进行测试实验。每次实验中,标准测试函数的维数N 为20。3 种算法的参数设置信息如表4 所示。

表4 3 种算法参数信息Tab.4 Parameter information about three algorithms
在AWPSO 算法中,惯性权重w 随着适应度函数值进行自适应变化,公式为
式中:f 和w 分别为粒子当前的适应度和惯性权重;fmin和favg分别为当前所有粒子适应度的最小值和平均值;wmax和wmin分别为惯性权重的最大值和最小值。
由于每次实验结果不稳定,具有随机性,每种算法连续进行了50 次实验,实验结果如表5 所示。由表5 可以看出,对于标准测试函数f1~f6,ISBO 的收敛精度明显优于SBO 和AWPSO 算法。其中对于标准测试函数f5和f6,ISBO 算法的收敛效果最为明显,其收敛结果达到了理论最优值0。
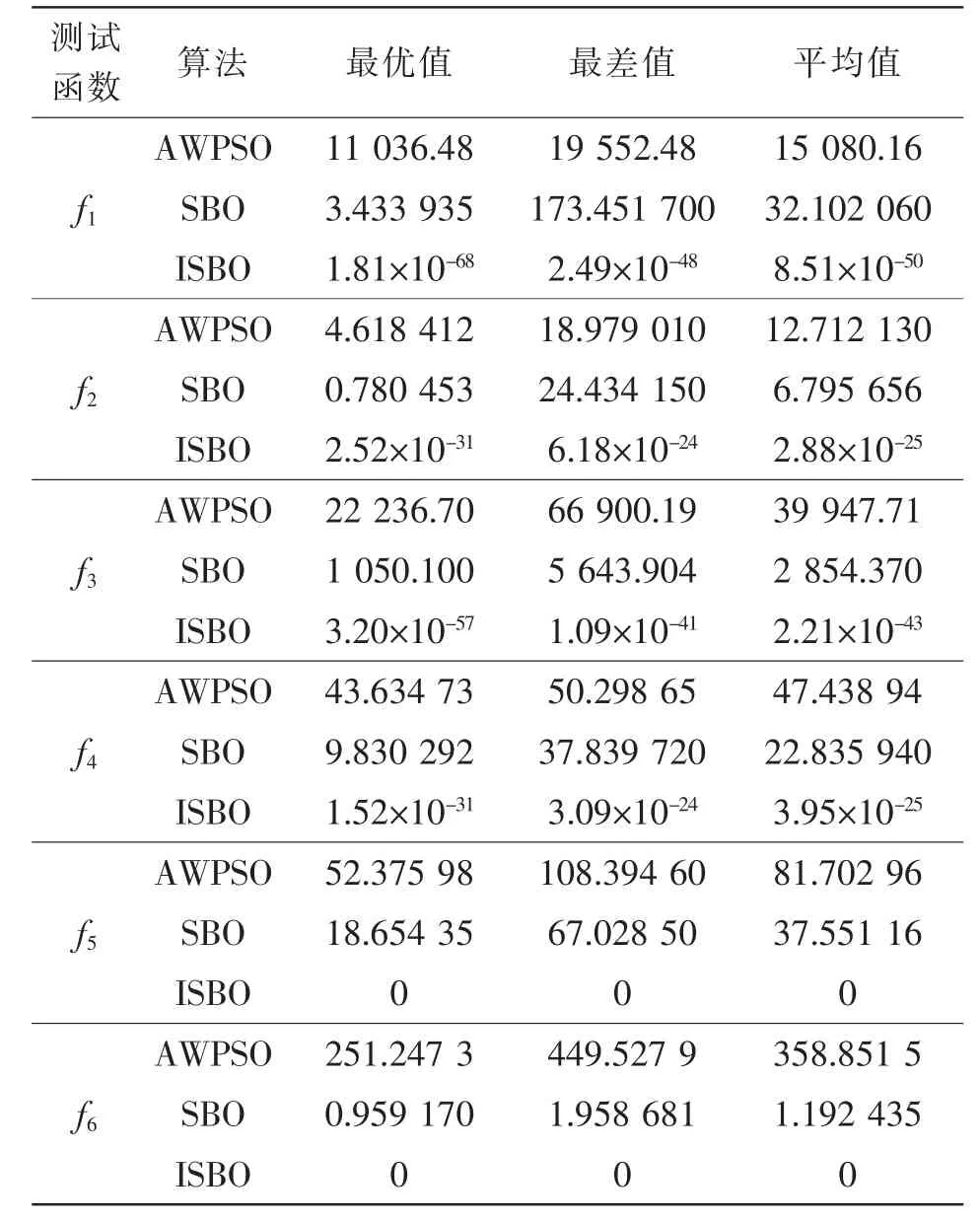
表5 实验结果Tab.5 Experimental results
综上分析,无论是单模态函数还是多模态函数,ISBO 算法的收敛精度明显优于SBO 和AWPSO 算法。因此本文可以将ISBO 算法应用到锂离子电池模型参数辨识过程中,从而建立高精度的等效电路模型。
3 Thevenin 模型原理及实验设计
3.1 Thevenin 模型原理
由于Thevenin 模型具有结构简单,含有较少参数和能够描述电池动态特性的优点[17-18],故本文选择对Thevenin 模型进行分析。Thevenin 模型中所需辨识的参数有欧姆内阻R0、极化电阻Rp和极化电容Cp。Thevenin 模型端电压的离散化表达式为
式中:Δt 为系统采样时间间隔;iL,k、Ut,k、Uocv,k和Up,k分别为k 时刻电池的电流、端电压、开路电压和极化电压;R0,k、Rp,k和Cp,k分别为k时刻电池的欧姆内阻、极化电阻和极化电容。
3.2 实验平台及对象
实验设备为新威尔CT-4008 电池检测系统,通过连接上位机可以设置电池的运行工况。电池实验平台如图2 所示。实验采用2 种不同类型圆柱形锂离子电池,其型号分别为LR1865SZ(下文简称A 型)和LR1865LA(下文简称B 型)。A 型和B 型电池额定容量分别为2 400、2 000 mA·h。对测试电池在室温条件下进行了开路电压OCV(open circuit voltage)实验、动态应力测试DST(dynamic stress test)工况和US06 工况实验。3 种实验的采样时间间隔均为1 s。

图2 电池实验平台Fig.2 Experimental platform of battery
3.3 实验设计
实验1:OCV 实验。A 型电池100% SOC(满电状态),以恒流0.5C 放电,放出额定容量10%后静置1 h,循环执行该放电和静置过程,直到电池电压到达放电截止电压,此时认为电池为0% SOC。0%SOC 电池静置1 h 后,以0.5C 恒流充电,充入额定容量10%后静置1 h,循环执行该充电和静置过程直到电池达到额定容量的90%,电池进入恒流恒压充电阶段,恒压为4.2 V。恒压充电结束认为电池SOC 为100%。B 型电池OCV 实验不同之处在于:A型电池以0.5C-额定容量10%-静置1 h 为一个处理单元,B 型电池以0.5C-额定容量5%-静置1 h 为一个处理单;A 型电池和B 型电池放电截止电压分别为3.0、2.5 V。
实验2:不同工况实验。电池在实际使用过程中并非完全进行恒流充电和放电,故选择电流、电压的变化较为剧烈的DST 工况和US06 工况来模拟电池实际使用时的情况。一个完整的DST 工况和US06 工况的时间分别为360、596 s。DST 工况和US06 工况电流曲线如图3 所示。

图3 不同工况电流曲线Fig.3 Current curves under different working conditions
A 型电池和B 型电池在OCV 实验过程中不同SOC 下的OCV 如表6 所示。由表6 可知,A 型电池和B 型电池充电过程中,OCV 随SOC 增加而增加;电池放电过程中,OCV 随SOC 减小而减小;同一SOC 下充电OCV 均略高于放电OCV。
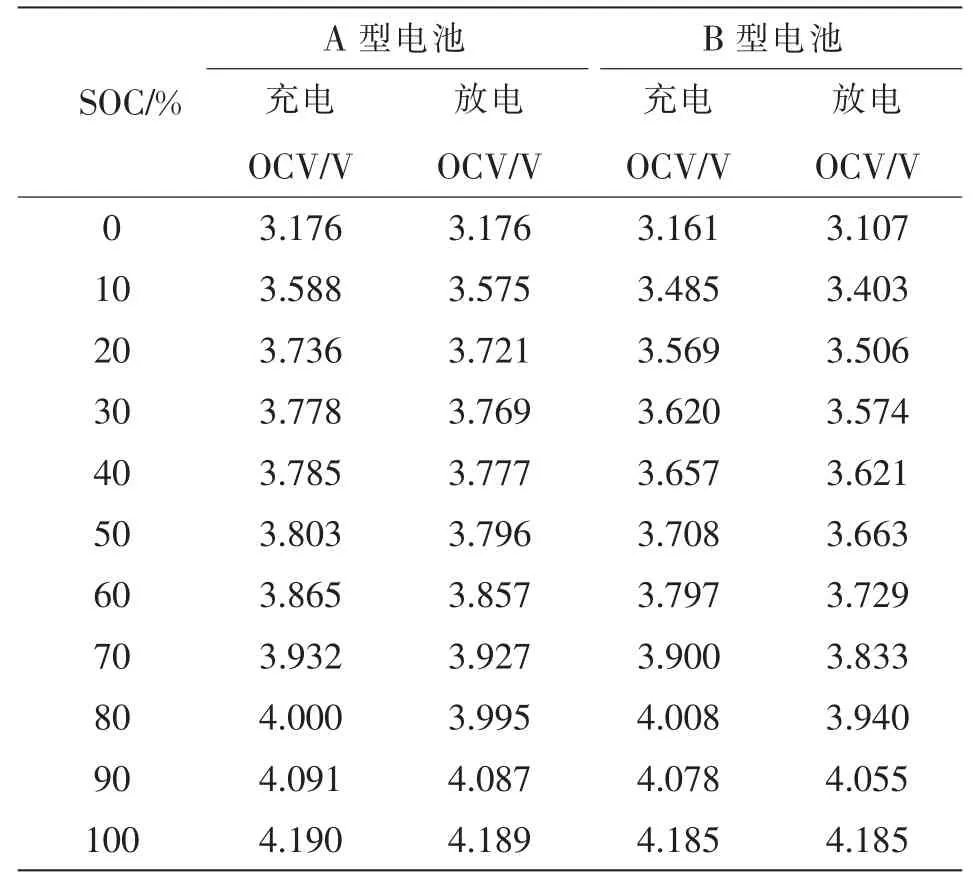
表6 2 种电池在不同状态下的OCVTab.6 Values of OCV of two batteries in different states
4 基于ISBO 算法的模型参数辨识
4.1 OCV-SOC 曲线拟合
由于锂离子电池迟滞效应的影响,相同SOC 下充电时电池的OCV 略高于放电时的OCV[19]。为了减小迟滞效应的影响,本文将每个SOC 对应的充放电开路电压的平均值作为此状态下的开路电压。通过Matlab 软件中的cftool 工具箱对OCV-SOC 曲线进行不同阶数多项式的拟合,结果表明:A 型电池5阶多项式拟合效果最好,拟合系数R2=0.999 6。B 型电池8 阶多项式拟合效果最好,拟合系数R2=0.999 9。具体拟合公式分别为
4.2 目标函数
以在整个采样时间内设备采集得到的端电压与电池模型仿真得到的端电压之间的累积误差作为目标函数,其计算公式为
式中:N 为采样时间总数;Uk为k 时刻设备测量得到的电压;Ut,k为k 时刻电池模型仿真得到的端电压。
4.3 基于ISBO 算法的模型参数辨识
采用ISBO 算法对Thevenin 模型进行参数辨识的流程如图4 所示。
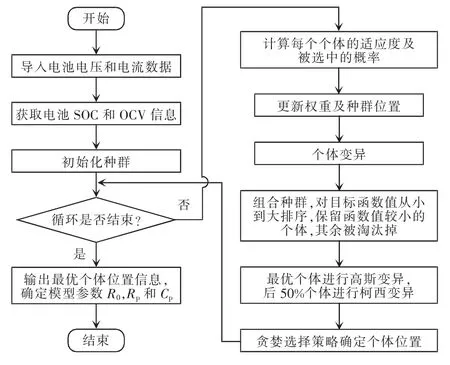
图4 基于ISBO 算法的模型参数辨识流程Fig.4 Flow chart of model parameter identification based on ISBO algorithm
5 实验结果及分析
5.1 不同算法参数辨识结果和分析
采用AWPSO、SBO 和ISBO 方法辨识Thevenin模型中的参数。以均方误差MSE(mean square error)、平均绝对误差MAE(mean absolute error)、平均绝对误差百分比MAPE(mean absolute percentage error)和决定系数R2(coefficient of determination)作为各方法参数辨识结果的评价指标,其中R2越接近1,模型参数辨识效果越好,其余的指标越小,模型参数辨识效果越好。MSE、MAE、MAPE 和R2的计算公式分别为
以上文所述OCV 实验为参数辨识工况,连续进行50 次测试实验,模型仿真电压各误差指标如表7 所示。
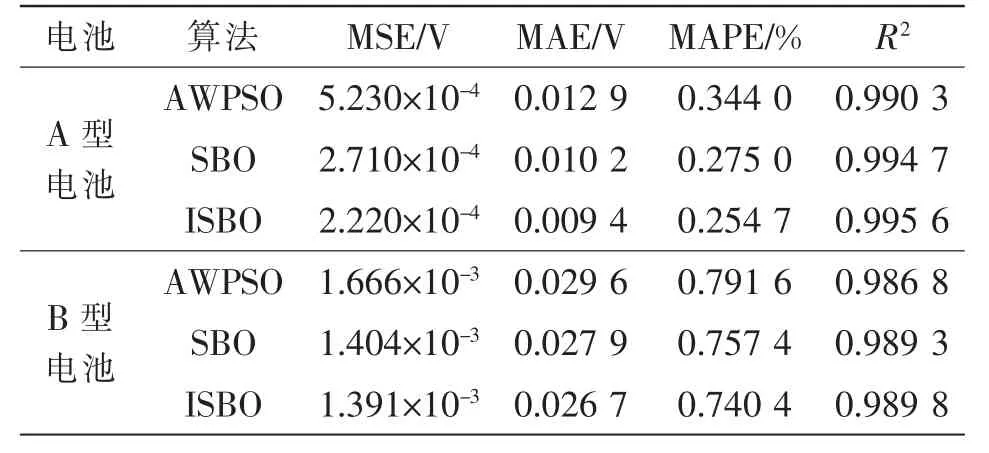
表7 OCV 实验输出电压平均误差统计Tab.7 Average error statistics of output voltage in OCV experiment
A 型电池某次实验中,3 种算法在OCV 实验下建立的模型仿真得到的电池端电压及端电压误差情况如图5 所示。
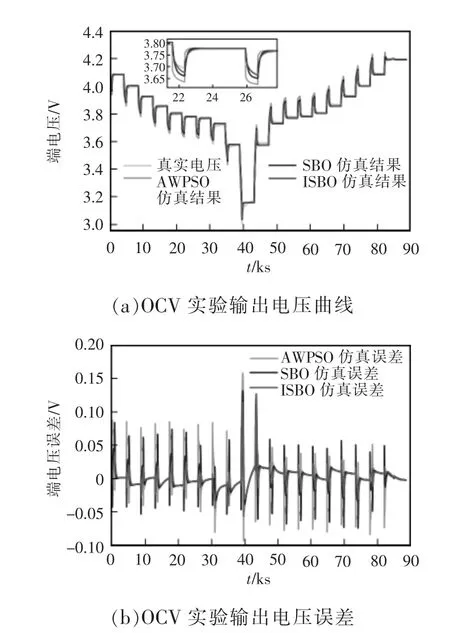
图5 OCV 实验下的输出电压及误差Fig.5 Output voltage and errors in OCV experiment
由表7 和图5 可知,2 种电池在OCV 实验下通过ISBO 算法建立的模型仿真端电压误差的各项指标均明显优于SBO 算法和AWPSO 算法。因此,采用ISBO 算法建立的Thevenin 模型优于SBO 算法和AWPSO 算法。
5.2 ISBO 算法对Thevenin 模型参数辨识的通用性验证
利用第5.1 节参数辨识结果作为模型参数,使用DST 工况和US06 工况数据验证ISBO 算法对OCV 工况辨识得到的参数具有通用性和适用性。表8 为上述50 次连续实验对应的参数辨识结果在2 种工况下的模型输出电压平均误差统计。

表8 DST 和US06 工况输出电压平均误差统计Tab.8 Average error statistics of output voltage under DST and US06 conditions
图6 和图7 展示了A 型电池在某次验证实验中在DST 和US06 工况下3 种算法建立的模型电压及误差。需要说明的是,为便于显示3 种算法的对比结果,图7 中DST 和US06 工况输出电压误差曲线中的数据点的采样时间间隔为50 s。

图6 DST 和US06 工况输出电压Fig.6 Output voltage under DST and US06 conditions
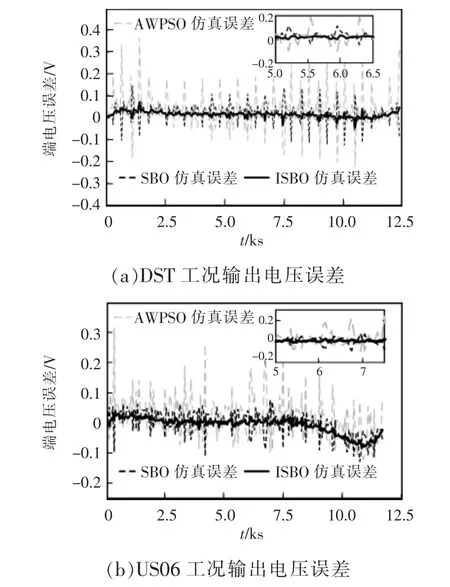
图7 DST 和US06 工况输出电压误差Fig.7 Errors of output voltage under DST and US06 conditions
由图6、图7 和表8 可知:2 种电池在DST 和US06 工况下,通过ISBO 算法建立的Thevenin 模型各项误差指标均优于SBO 和AWPSO 算法。3 种算法对Thevenin 模型参数辨识均具有通用性,其中采用ISBO 算法建立的Thevenin 模型精度较高且模型精度不受电池工况的影响。实验结果也说明在OCV 实验下建立的Thevenin 模型,能够仿真电池在DST 和US06 工况下的静态特性和极化现象。
5.3 不同工况下的模型参数辨识结果及验证分析
为验证ISBO 算法进行参数辨识不依赖于特定工况,以A 型电池为例,将DST 工况和US06 工况作为参数辨识工况,其他工况作为验证工况。每种实验均连续进行50 次。
(1)以DST 工况作为参数辨识工况,参数辨识结果用于OCV 工况和US06 工况。
(2)以US06 工况作为参数辨识工况,参数辨识结果用于OCV 工况和DST 工况。
参数辨识时各误差结果及对应的参数验证各误差结果见表9 和表10。
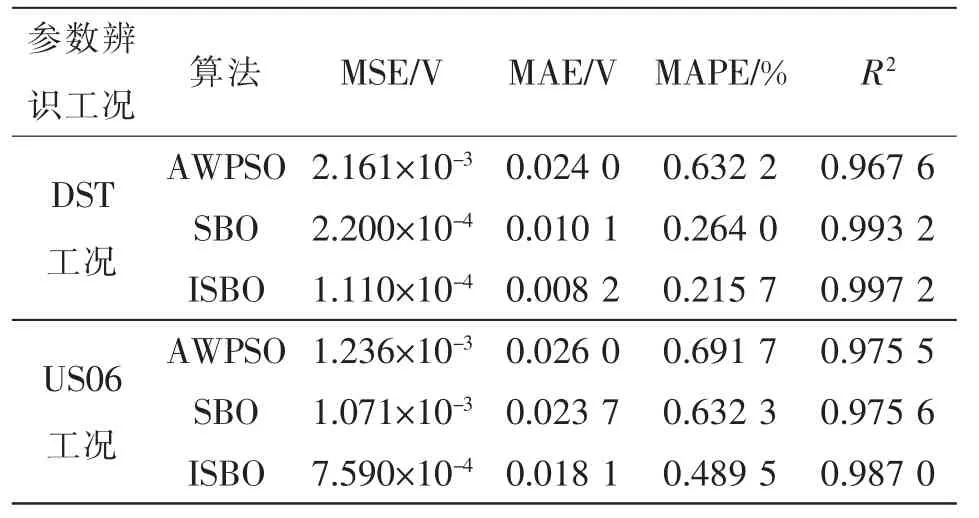
表9 DST 和US06 工况参数辨识平均误差统计Tab.9 Average error statistics of parameter identification under DST and US06 conditions
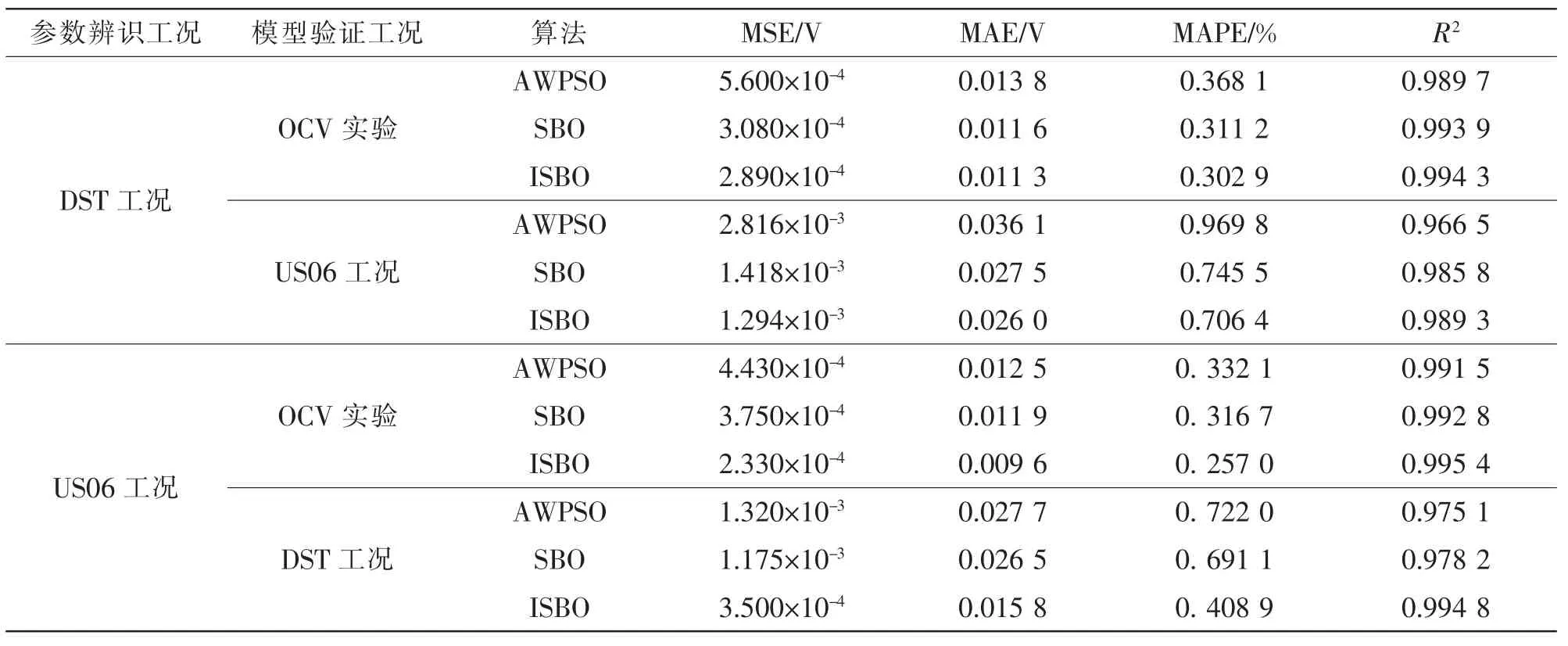
表10 模型验证工况输出电压平均误差统计Tab.10 Average error statistics of output voltage under model verification conditions
由表9 可知:在以DST 和US06 工况作为参数辨识工况下,通过ISBO 算法建立的Thevenin 模型各项误差指标均优于SBO 和AWPSO 算法。3 种算法对Thevenin 模型参数辨识均具有通用性,其中采用ISBO 算法建立的Thevenin 模型精度较高且模型精度不受电池工况的影响。
由表10 可知:在以DST 和US06 工况作为参数辨识工况,其他2 种工况作为模型验证工况下,通过ISBO 算法建立的Thevenin 模型各项误差指标均优于SBO 和AWPSO 算法。利用DST 工况下建立的Thevenin 模型,能够仿真电池在OCV 实验和US06 工况下的静态特性和极化现象。利用US06工况下建立的Thevenin 模型,能够仿真电池在OCV 实验和DST 工况下的静态特性和极化现象。
结合上文得到结论:在OCV 实验下建立的Thevenin 模型,能够仿真电池在DST 和US06 工况下的静态特性和极化现象。综上分析,利用一种工况下建立的Thevenin 模型,能够仿真电池在其他工作条件下的静态特性和极化现象。
6 结论
基于SBO 算法收敛精度低和收敛速度慢的缺点,本文采用惯性权重、柯西变异、高斯变异和贪婪选择策略来改进SBO 算法,提出了ISBO 算法,并利用标准测试函数验证了ISBO 算法的有效性。对电池在室温下进行了OCV 实验、DST 和US06 工况实验,其中利用OCV 实验下的数据对锂离子电池Thevenin 模型进行参数辨识,利用DST 和US06 工况下的实验数据验证参数辨识结果的通用性。通过分析得到以下结论:
(1)利用标准测试函数验证了ISBO 算法对于单模态函数、多模态函数、低维空间和高维空间均具有有效性。与SBO 算法相比,ISBO 算法的收敛精度明显提高。
(2)AWPSO、SBO 和ISBO 算法对锂离子电池Thevenin 模型参数辨识均具有通用性,其中采用ISBO 方法建立的Thevenin 模型精度较高且模型精度不受电池工况的影响。
(3)利用一种工况下建立的Thevenin 模型,能够仿真电池在其他工况下的静态特性和极化现象。
