新型三相电压型准Z 源AC-AC 变换器

李昊舒，徐 飞（中国电源学会会员），赵志远

（1.山东化工职业学院机电工程学院，潍坊 261000；2.滨州职业学院机电工程学院，滨州 256600；3.国网山东省电力公司齐河县供电公司，德州 251100）

为克服传统调压器电路的固有缺陷，文献[1]提出传统Z 源升压变换器。之后，一些改进的新型Z源逆变器被广泛研究[7-17]。其中，文献[4]在Z 源网络的基础上提出了准Z 源网络拓扑[5]，准阻抗源变换器的出现是阻抗源变换器理论和拓扑的一个新的发展[2]。这种电路拓扑一经提出就引起高校和工业界的广泛关注，在整流电路、交直流调压电路、逆变电路中得到深入研究。与传统阻抗源变换器相比，准阻抗源变换器可以克服传统阻抗源变换器的某些缺陷，如在电压型电路中，阻抗源网络电容器电压过高[2，6]。另外，相比于传统相控式交流调压器只能实现升压或者降压的单一作用，准Z 源AC-AC变换器则既能完成升压也能实现降压，还可以实现电压的变相，即使输出和输入电压同相或反相。除此以外，还可以克服传统斩控式交流调压器由于电路中功率开关器件的共态导通或共态关断导致的电源短路或电感性电流开路的问题[3]。提高了系统稳定性与开关管寿命[5]。对于单相准Z 源交流调压的研究已经相对成熟，但是对于三相准Z 源电路的研究则相对较少。本文提出一种新型三相准Z 源AC-AC 变换器电路拓扑，对电路进行了分析，并利用Matlab/Simulink 搭建了仿真模型，进行了仿真研究，对仿真结果进行了分析，最后在仿真模型的基础上搭建出了实物实验电路，得到了实验电路的波形，通过实验结果验证了理论分析和仿真结果的科学性和正确性。

1 三相准Z 源交流调压器的拓扑结构

新型三相准Z 源AC-AC 变换器电路拓扑如图1所示，电路由三相对称的电感、电容以及全控双向开关组成。其中，电感和电容是电路的核心部分，分为准Z 源部分和滤波部分，可以实现两种功能：准Z 源部分的电感和电容实现变压，后面部分的电感和电容实现滤波。全控双向开关为电路的控制部分，是由IGBT 和二极管反向并联以后面对面串联组成的电路模块，其可以通过PWM 信号来实现对电路的控制。其控制方法是每相中的两个可控双向开关在一个开关周期内互补导通，为了保证三相对称，PWM 信号需对电路中的双向开关同步控制，如图1 中Sa1、Sb1、Sc1的状态需同步，Sa2、Sb2、Sc2的状态需同步。通过调节占空比D 可以实现对电压的调节变换。

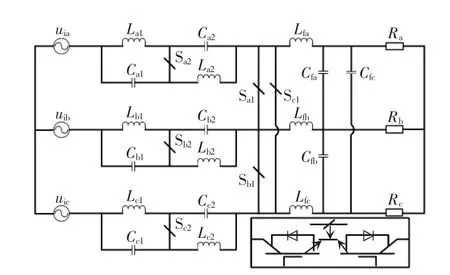
图1 新型三相准Z 源AC-AC 变换器电路拓扑Fig.1 Circuit topology of novel three-phase quasi-Z source AC-AC converter

2 三相准Z 源交流调压器的工作状态分析

因为电路中存在二极管、开关管等非线性元件，不能采用已有的线性分析理论，但是当时间基准取地无穷小时，这些非线性元件在某些时刻可以当成线性元件来处理[7]。又因为电源频率远低于可控双向开关的开关频率，所以在分析电路的过程中可以将输入信号近似成直流信号。根据可控双向开关的开关状态，可以分为两种电路状态，但是在这两种状态下，根据电流的流向，可分为以下五种工作状态（Sa1、Sb1、Sc1定义为Sx1，Sa2、Sb2、Sc2定义为Sx2，每一相滤波电感定义为Lfx，每一相滤波电容定义为Cfx）：

工作状态1：如图2（a）所示。Sx1闭合，Sx2断开，电源和准Z 源中的电容一起给准Z 源中的电感充电，负载中的电能由滤波电感Lfx提供，电流方向如图2（a）中所示。

图2 5 种工作状态Fig.2 Five operating states

工作状态2：如图2（b）所示。所有可控双向开关的开通和关断的状态和状态1 完全相同，但是，滤波电感Lfx中电流的方向与状态1 中Lfx中电流的方向相反，当滤波电感Lfx中的电能消耗完以后，其中的电流变为0，这时滤波电容Cfx中的电能会流向滤波电感Lfx，即滤波电容给滤波电感充电，滤波电感Lfx中的电流相对于状态1 会发生反向，并且逐渐增大。

工作状态3：如图2（c）所示。Sx1断开，Sx2闭合，这时若滤波电感Lfx中的电流是反向的，准Z 源网络由滤波电容Cfx提供，三相电源中的每一相电源和每一相准Z 源网络中的电感给每一相准Z 源网络中的电容充电，此时，三相负载中每一相电阻的电能来自于每一相电源和各自准Z 源网络中的电感。

工作状态4：如图2（d）所示。此时，可控双向开关的状态和工作状态3 中的状态完全一致，但是，这时每一相滤波电感Lfx中的电流与状态3 时相反，是正向流动的，此时每一相电源和各自准Z 源网络中的电感给各自的负载提供电能，各相准Z 源网络中的电感中的电能逐渐减少，电流也随之逐渐减小。

工作状态5：如图2（e）所示。每一相准Z 源网络的电感中流过的电流逐渐减小，当其中的电流与各自准Z 源网络中滤波电容Cfx的电流大小相同时，三相电阻的每一相电阻的电能将由各自准Z 源网络中的电容提供。

以上5 种工作状态以Sx1和Sx2互补导通为前提条件，所以以PWM 信号来控制可控双向开关就可以达到控制输出电压的目的。根据可控双向开关的状态，可以将以上5 种工作状态划分为两大组情况，即Sx1闭合、Sx2断开和Sx1断开、Sx2闭合，分别定义为A状态和B 状态，接下来将对两大组状态进行定量分析，推导出输出电压和输入电压之间的关系。

3 三相准Z 源交流调压器升压比的推导

在推导升压比的过程中需要用到两个关系：Sx1断开时，三相电源中性点和三相负载中性点的瞬时电压关系；Sx1闭合时，三相电源中性点、三相负载中性点和可控双向开关Sx1处的瞬时电压关系。如果运用推导计算的方法过程会非常繁琐，此处用Matlab/Simulink 进行仿真得到以上两个关系。在Sx1导通占空比为0.3 时进行仿真。图3 是三相电源中性点和三相负载中性点之间点位差仿真图。

图3 三相电源和三线负载中性点电位差Fig.3 Neutral point potential difference between threephase power supply and three-wire load

图4 是三相电源中性点和可控双向开关Sx1处电压关系的仿真结果。

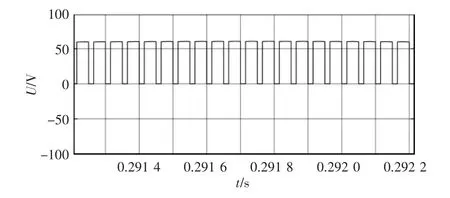
图4 三相电源中性点和Sx1 处电压关系Fig.4 Voltage relationship between three-phase power supply neutral point and Sx1

图5 是三相负载中性点和Sx1处的电压关系仿真结果。

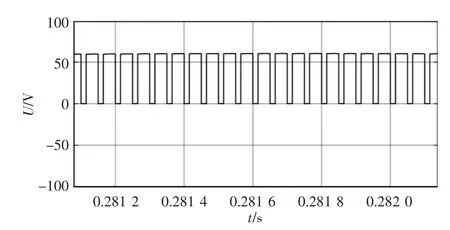
图5 三相负载中性点和Sx1 处电压关系Fig.5 Voltage relationship between three-phase load neutral point and Sx1

由仿真结果可知，在三相负载对称的前提下，可以得出如下两个结论：

（1）由图3 可知，当电路中电感和电容充放电完成，调压器电路进入稳定状态后，三相电源中性点和三相负载中性点处的电位差时刻为0。

（2）由图4 和图5 可知，当可控双向开关Sx1闭合时，三相电源中性点、三相负载中性点以及Sx1处的电位差为0。

根据以上仿真结果，可得出Sx1处于不同状态时的等效电路图，分别如图6 和图7 所示。

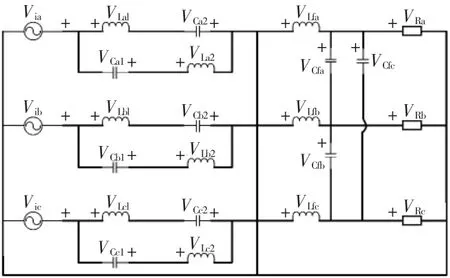
图6 A 状态（Sx1 闭合、Sx2 断开）Fig.6 State A（Sx1 on and Sx2 off）

图7 B 状态（Sx1 断开、Sx2 闭合）Fig.7 State B（Sx1 off and Sx2 on）

A 状态的等效电路图如图6 所示。

根据KVL 得

B 状态的等效电路图如图7 所示。

根据KVL 得

通过上面的分析，令Ts为开关周期，Sx1导通的占空比为D，则Sx1的导通时间为DTs，（1-D）Ts为Sx2的导通时间。令T 为电源周期。在一个周期内，La1、Lb1、Lc1和La2、Lb2、Lc2两端的电压为0。由以上关系式，在一个电源周期内可以得到关系式为

在双向开关的一个开关周期之内，电路中电容Cx1和Cx2两端的电压基本不变，可以得出关系式为

根据关系式（7）到关系式（10）可得

整理后可得

滤波电感Lfx在一个电源周期内电压平均值为0，可得关系式为

根据关系式（14）可得

通过整理，最后可以得到输入电压和输出电压的关系为

4 仿真结果及分析

在Matlab/Simulink 环境下对文中提出的三相准Z 源AC-AC 变换器电路进行建模并仿真，图8（a）为全部电路的仿真模型，图8（b）为可控双向开关仿真模型。仿真模型的电路参数如下：三相对称交流电源电压为24 V，频率为50 Hz，三相准Z 源网络中Lx1和Lx2选取500 μH，电容Cx1和Cx2 选取4.7 μF，双向开关Sx1和Sx2的开关频率为20 kHz，滤波电感Lfx选取100 μH，滤波电容Cfx选取100 μF，三相对称负载选取100 Ω。为与实际一致，便于采用嵌入式系统实现，仿真算法为离散模式，采样周期为10 ns[5]。

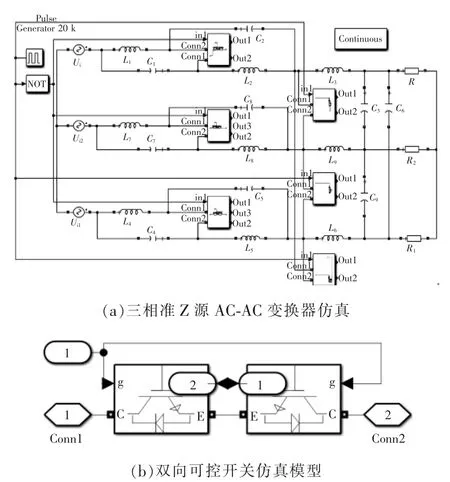
图8 主电路及可控开关仿真Fig.8 Simulation of main circuit and controllable switch

图9 和图10 为三相准Z 源AC-AC 变换器在D=0.2 和D=0.8 时的输出结果仿真波形。可看出前期输出电压不稳定，这是因为在刚开始通电后，准Z 源网络中的电感和电容需要一定时间完成充分充放电。在D 分别为0.2 和0.8 时，电路分别在0.05 s 和0.1 s 进入稳定状态，根据式（16）计算得出输出电压的绝对值应分别为32 V 和8 V，与仿真结果相同。

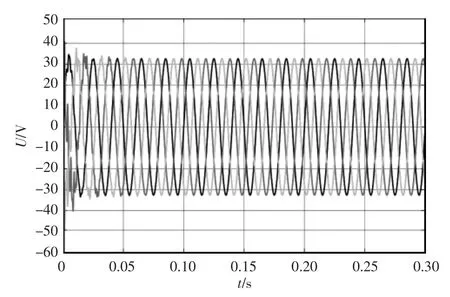
图9 D=0.2 时输出电压波形Fig.9 Output voltage waveform when D=0.2

图10 D=0.8 时输出电压波形Fig.10 Output voltage waveform when D=0.8

图11 为流过电感的电流仿真波形图。可见电流有一部分是反向的，所以电感内流过的电流是连续的。由于双向可控开关的基础部件使用的是IGBT 与二极管反并联的形式，所以准Z 源网络中电感Lx1和Lx2中的电流可以反向流动，因此双向可控开关的寄生电容两端积累的多余的电能可以被释放掉，从而减小了开关应力。

图11 电感中电流波形Fig.11 Current waveform of inductor

图12 为D=0.2 时双向可控开关中电流和两端电压的仿真波形。其中锯齿波1 为电流波形，矩形波2 为电压波形。通过仿真波形可以看出，可控双向开关两端的电压在其导通前已经降为0 V，实现了零电压开通，而零电压开通有如下好处：

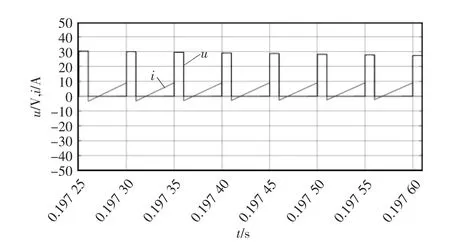
图12 可控双向开关中电流和两端电压Fig.12 Current and voltage of controllable bidirectional switches

（1）降低因电网波动产生的瞬间电流冲击，延长设备寿命。

（2）降低开关管的损耗，使在开关管上消耗的电能减少，可以有更多的电能提供到负载，因而提高整个调压电路的效率。

图13 和图14 分别为D=0.2 时电容中电流和两端电压的仿真波形图。

图14 电容中电流波形Fig.14 Current waveform of capacitor

由式（13）计算可得在D=0.2 时，电容两端的电压应为8 V，与图13 的仿真结果相同。

5 实验结果

根据仿真模型搭建实验电路，如图15 和图16所示。实验样机如图17 所示。

图15 D=0.2 时的升压波形Fig.15 Boost waveform when D=0.2

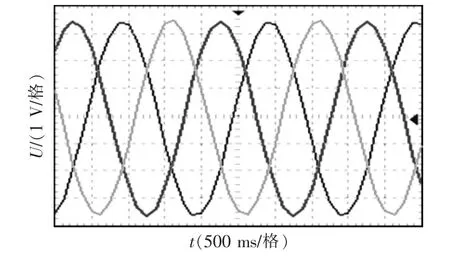
图16 D=0.8 时的降压波形Fig.16 Buck waveform when D=0.8

图17 实验样机Fig.17 Experimental prototype

出于安全考虑，通过三相变压器将电压降至12 V 作为输入电压，控制的核心芯片采用STM32 F103，利用其发出PWM 信号，采用两块落木源KA962D 驱动板对IGBT 进行驱动，可控双向开关采用FGA25N120，参数如下：Lx1和Lx2选取500 μH，电容Cx1和Cx2选取4.7 μF，双向开关Sx1和Sx2的开关频率为20 kHz，滤波电感Lfx选取100 μH，滤波电容Cfx选取100 μF，三相对称负载选取100 Ω。分别取D=0.2 和D=0.8 时进行试验，其中D=0.2 时为升压，D=0.8 时为降压。

当D=0.2 时，理论输出波形应升为16 V，由实验波形图15 可知，实际输出为18 V 左右，与理论分析非常接近。

当D=0.8 时，理论输出波形应降为4 V，由试验波形图16 可知，实际输出为3.5 V 左右，与理论分析十分接近。

经过实验，可知输出效率在88%左右，鉴于是在实验室环境下得到的结果，应用于实际工程中时，可能会有所不同。

6 结论

将单相准Z 源AC-AC 调压器电路应用到三相电路拓扑中，对电路的工作原理及过程进行分析，对输入和输出电压关系进行了推导，得到电压增益。用Matlab/Simulink 进行了仿真研究。最后搭建实验电路并得到实验结果。仿真和实验结果表明，三相准Z 源AC-AC 调压器电路的可控双向开关可以实现零电压开通，电感中电流不会断续，使电路的通态损耗降低，从而减少了在调压器电路上的电能消耗，可以将电源提供的电能更多的传送到负载，从而提高了效率，使系统稳定性和开关管的使用寿命得以提升。

此外，电路的经济性方面仍有需要提升的空间，可采用如下办法：

（1）有较多无源元件，如电感线圈可以购买原材料后自行绕制。

（2）在升压要求不高，但是电流很大或频率很高的场合，可以使用MOSFET 替代IGBT。