邮轮上层建筑分段吊装评估与参数敏感性分析

葛珅玮,曾骥,贾君瑞,董小伟,陈洪钊

(1.江苏航运职业技术学院,江苏 南通 226010;2.上海海事大学 a.商船学院;b.海洋科学与工程学院,上海 201306;3.招商局邮轮制造有限公司,江苏 南通 226100)

目前国内船体分段的吊装研究主要以货船与海工结构物为对象,这些结构的板材、骨材尺寸一般较大,因此强度、刚度问题一般不大[1-2]。对于邮轮上建来说,其板材、骨材均相对较小,且其舷侧门窗开孔大、布置十分密集[3],见图1,导致其结构刚度较弱。同时,为了提高邮轮的建造效率,在船体分段建造阶段会预装一些支架、玻璃门窗等舾装件,在吊装时,容易出现局部强度不足和变形过大的问题。过大的变形可能会进一步导致这些舾装件发生损伤,见图2。

图1 典型邮轮上建分段舷侧开孔

图2 典型邮轮结构吊装损伤图

因此,有必要对邮轮上建分段的吊装评估进一步研究,以保证分段结构的安全。为此,基于有限元数值分析,提出一种邮轮上建舷侧开孔分段吊装的评估流程,对某极地邮轮的典型上建分段吊装开展多方案评估,利用线性回归方法,对吊装参数进行敏感性分析。

1 邮轮分段吊装评估流程

1.1 强度评估

对于吊装方案的评估,首先要进行强度分析,只有强度满足要求了,再进行位移等其他的响应分析会有意义。利用有限元计算,可以得到分段结构的应力分布。基于ABS吊装规范要求[4],吊装时的许用应力为

[σe]=σy·SC

(1)

式中：σy为屈服应力;SC为许用应力系数,取0.75。

1.2 整体位移评估

分段吊装时整体结构会产生一定的位移,过大的位移不仅对分段的定位、船台合拢时的精控不利,而且可能会对分段预装的支架、管系等舾装件造成损伤,因此在吊装中必须控制结构的整体位移。参考CCS《邮轮规范》中对整船位移的规定[5],吊装中结构最大位移应控制如下。

ηa=δ/l≤1/400

(2)

式中：ηa为形变率;δ为最大位移;l为结构跨长。

1.3 舷侧开孔局部位移评估

邮轮分段结构在吊装时,舷侧的开孔框架结构会发生局部变形(见图3),图中虚线为开孔吊装前的位置,实线为吊装时的位置状态,舷侧框架在吊装前后产生了局部的相对位移。该位移不能过大,过大的位移可能对预装的玻璃门窗造成损伤。因此,不能仅凭吊装时的整体位移值判断邮轮分段吊装方案是否足够安全。

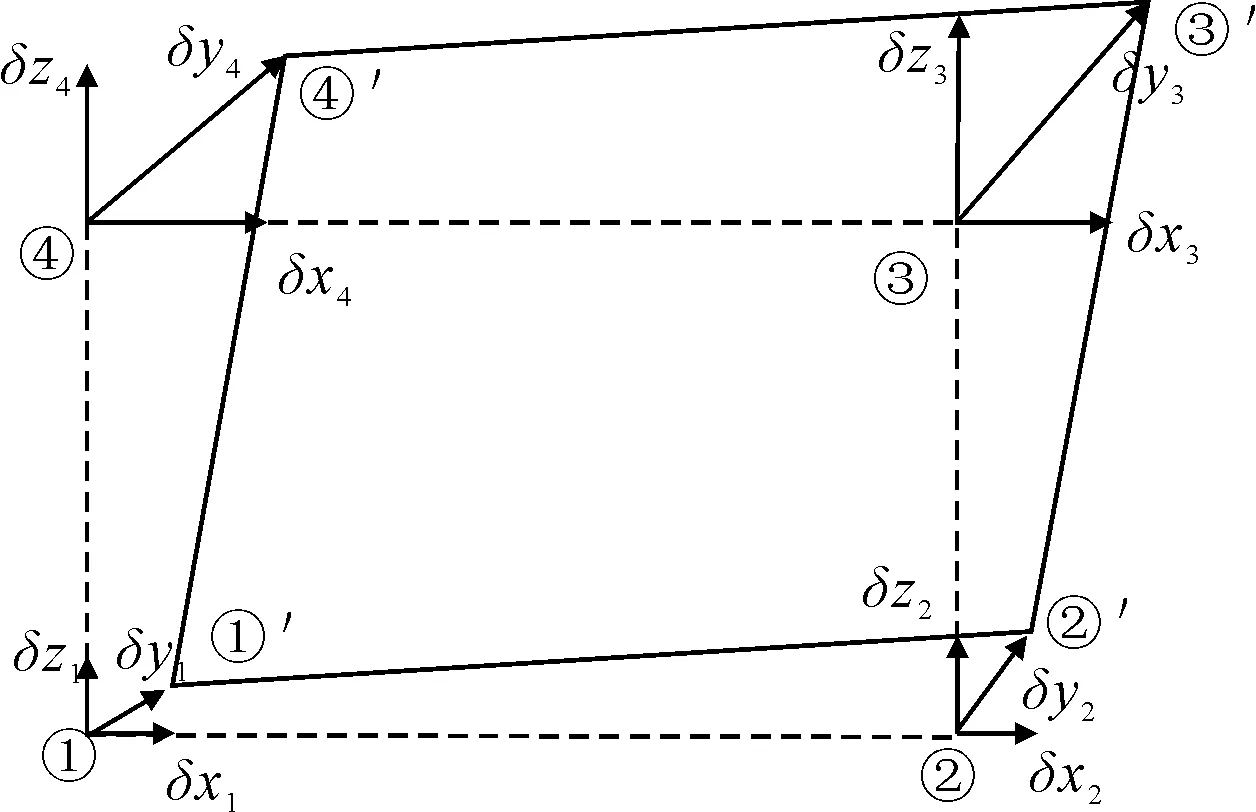
图3 开孔局部位移形式

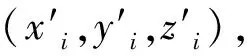
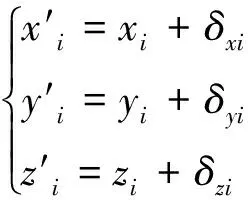
(3)

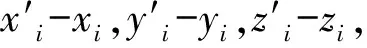
(4)

式中：i=1,2,3,4,j=1,2,3,4,且i≠j。

为保证开孔处门、窗等预装舾装件的安全,式(4)所得各方向局部位移值须满足局部变形控制要求。依据各船厂经验,局部结构的形变率应控制在2/1 000以内,即局部结构在1 000 mm长度内的最大位移值应小于2 mm[6]。

1.4 邮轮分段吊装方案评估流程

对邮轮上建分段吊装方案的评估流程总结如图4所示。首先对吊装方案进行有限元建模,然后进行结构应力分析,满足要求以后再进行整体结构的位移分析,最后对舷侧开孔进行局部位移分析。只有当上述所有的计算都满足要求时,该方案才是安全可行的。

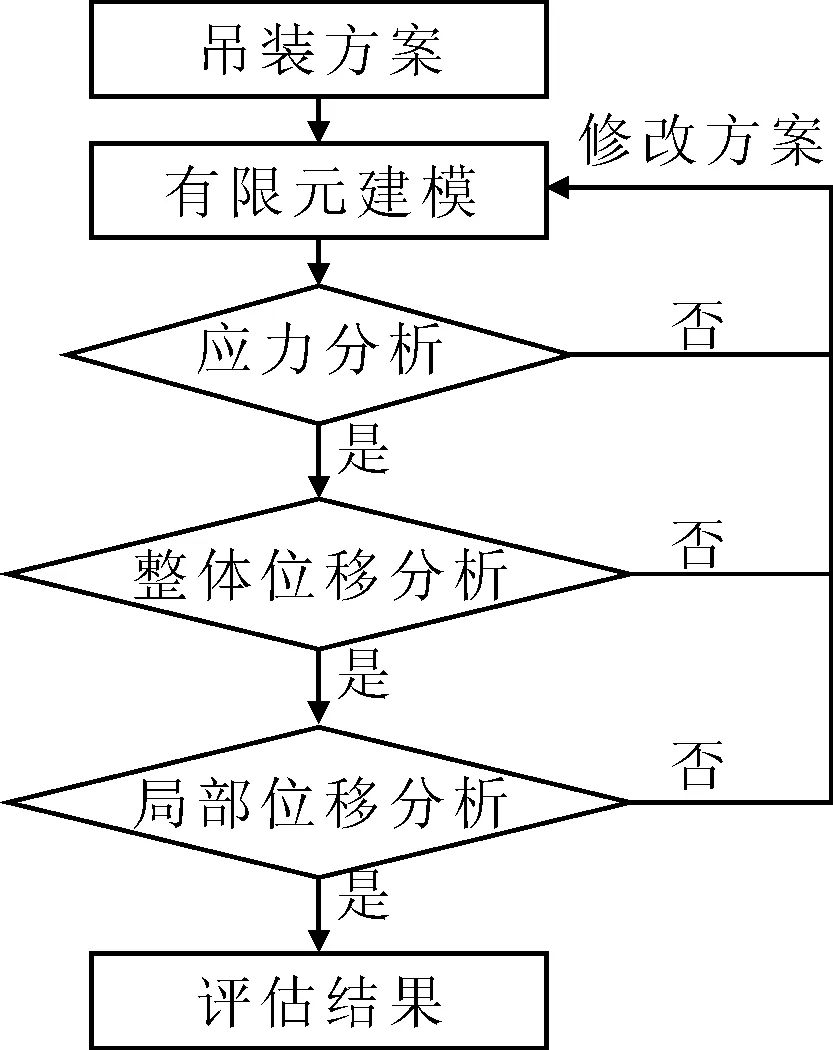
图4 邮轮上建分段吊装分析流程

2 吊装方案评估

2.1 有限元模型

利用FEMAP软件建立有限元模型,见图5。

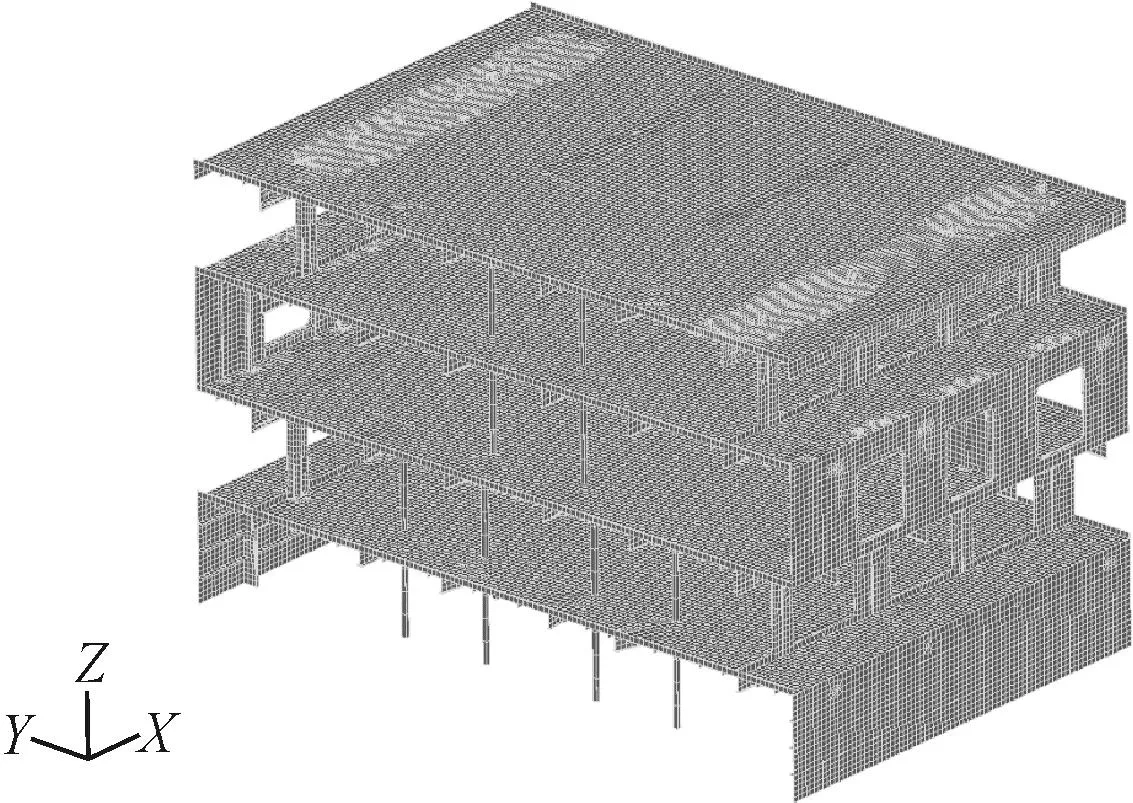
图5 分段结构有限元模型

模型中,x轴向船艏为正,y轴向左舷为正,z轴向上为正;舱壁、甲板、横梁、纵桁以及加强筋采用板单元模拟,支柱、底部水平支撑采用梁单元模拟;有限元网格尺寸150 mm×150 mm,吊耳附近区域采用网格尺寸不大于100 mm×100 mm。材料采用AH36高强钢。

边界条件设置为约束吊耳处节点线位移,即Tx=Ty=Tz=0;起吊时考虑一定冲击效应,载荷取1.2g。

2.2 结构应力与整体位移评估

各方案结构最大应力与整体最大位移见表1。

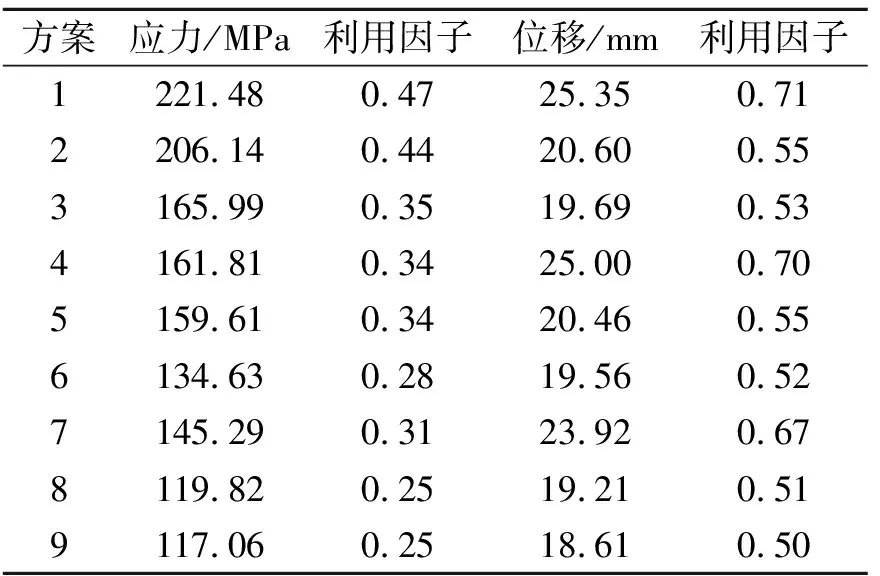
表1 结构最大应力与最大整体位移

由表1可以看出,所有方案的应力和整体变形都满足要求。最大应力达到许用应力的47%,最大位移达到许用值的71%,且最大位移占许用值的平均比例要比应力来的高,可见相比应力,整体位移是吊装分析的主控因素。

当吊耳布置一定时比较应力和位移,如方案1～3,可发现应力和位移随着加强构件的增多而不断减小,说明补强能有效的提高结构强度和刚度;但随着补强的大幅增大,整体位移降低的幅度却是不断减少的,说明仅通过局部补强,不能大量减少整体位移值。当补强相同时,比较应力和位移,发现应力有变化,但位移变化较小,这说明吊耳布置对改善应力有良好作用。此外,结构的最大应力主要发生在最上层甲板与吊耳的连接处,这说明吊耳的连接处是吊装强度评估的一个关键点。

2.3 舷侧开孔局部位移评估

进一步对舷侧开孔进行局部位移分析。选择变形较大的右舷的4～5甲板间的3处开孔作为分析对象,见图6。

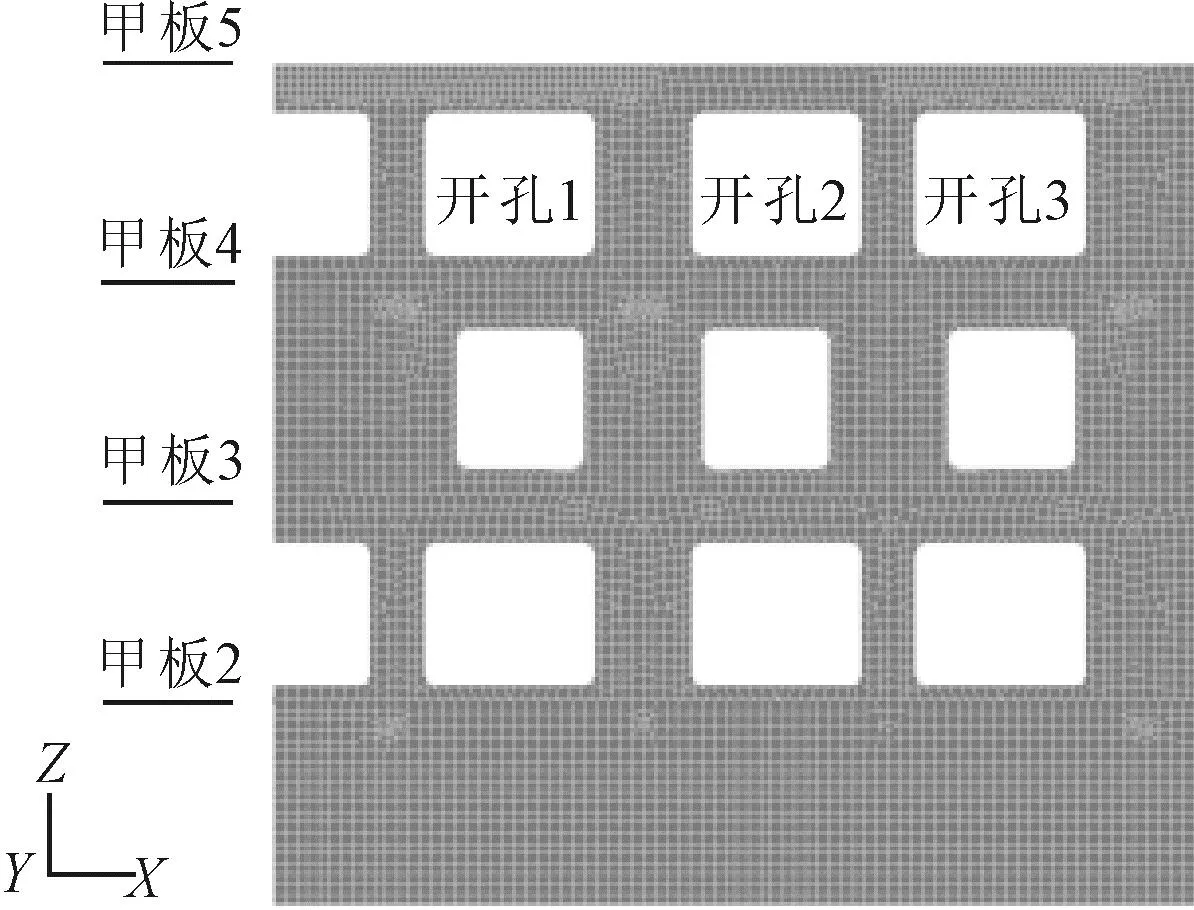
图6 舷侧结构开孔

计算得到这3个开孔的局部位移值与利用因子见表2。

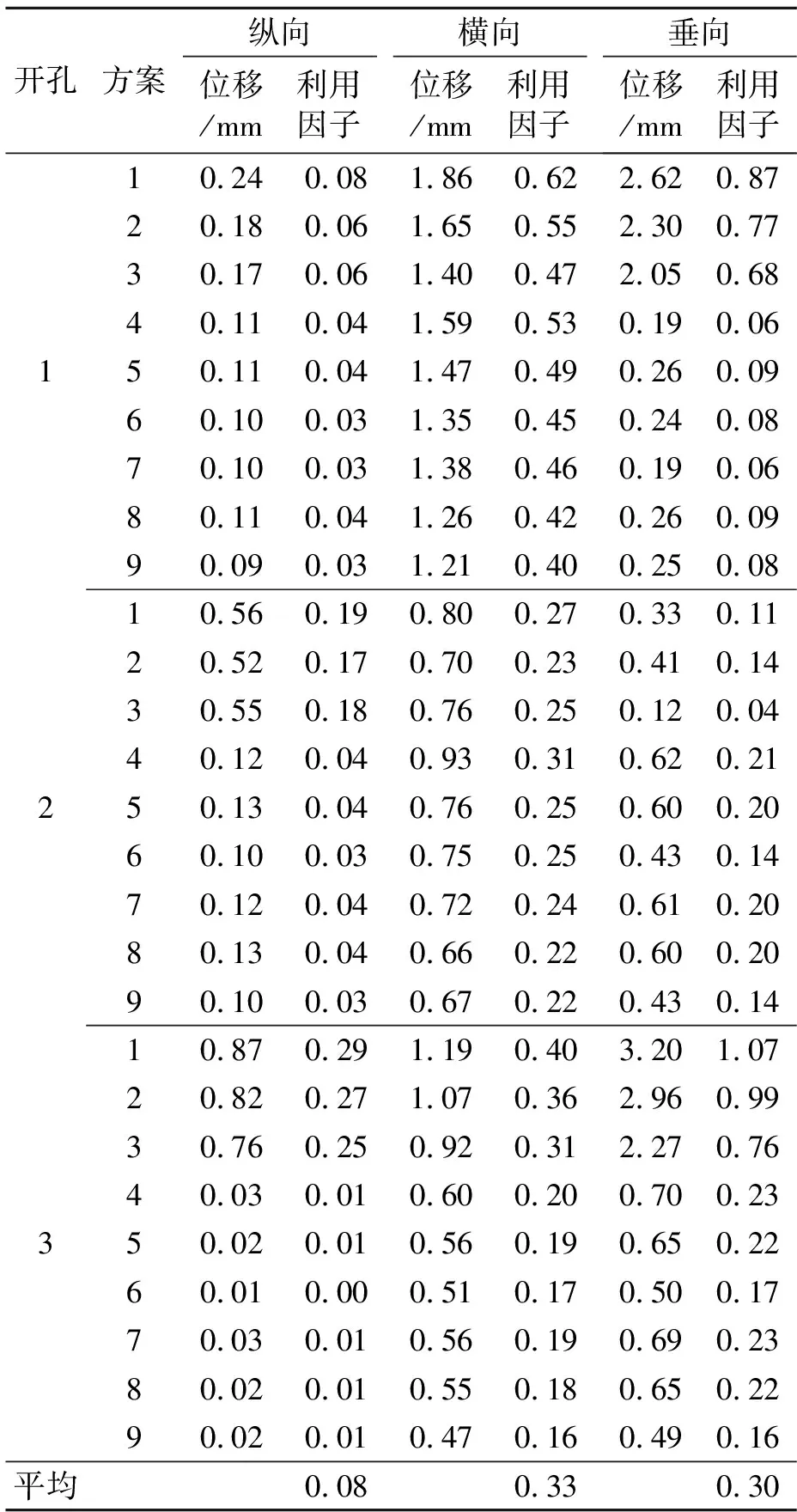
表2 舷侧开孔各方向的局部位移

由表2可见,3处开孔的局部位移有1个吊装方案不满足许用要求、且有1个方案达到许用值的99%,可见结构仅仅满足强度与整体变形的要求是不够的,也说明局部位移分析有必要。分析最大位移,吊装时纵向位移最小,横向位移次之,垂向位移最危险,且纵向位移占许用值得比例均很小,不足10%,因此评估时可忽略。比较3个开孔的局部位移,开孔2的位移最小,主要其位于吊点的中间,受力比较均匀;开孔1和3的局部位移较大,是因为其部分区域处于吊索(支点)的外部,类似于简支梁的外部,支撑较弱,因此位移较大。此外,从吊耳布置上看,方案1、4、7,随着吊耳布置均匀程度的增加,开孔的局部位移不断减少,尤其是垂向变形,最大降幅达到了78%(开孔3的方案1～4),这说明吊耳的均匀布置对降低开孔局部位移有良好的作用。

3 吊装参数敏感性分析

3.1 多元线性回归

多元线性回归分析是利用回归方程来确定因变量与2个或者2个以上变量间定量关系的数学分析方法。通过多元线性回归判定吊装应力、整体位移、局部位移与吊耳位置、补强方式之间的关系,并且通过回归方程中的系数,来判定吊装设计参数对结构响应的敏感程度,从而为吊装方案的设计提供优先选择的方式。

在回归分析时,分别对吊耳布置位置按照位置一至位置三、临时补强方式按照方式一至方式三进行编码赋值,设吊装时结构最大应力为y1,整体位移为y2,局部位移为y3;吊耳布置位置定义为x1,临时补强方式定义为x2,则回归方程为

yi=αi0+αi1·x1+αi2·x2

(5)

式中：αi0、αi1、αi2分别为常数及相关系数,i= 1、2、3。通过进行回归分析,计算上述参数。

3.2 回归检验与参数敏感性分析

对上述应变量与变量回归分析,并进行假设检验,结果见表3。从方差R2的表现上看,应力的R2值十分接近1,说明其回归拟合程度很好;整体位移、局部位移的R2值相对较小,说明这2个应变量的拟合精度相对较差,但仍有效。从变量共线性表现来看,VIF值全部远小于10,可见回归变量之间没有多重共线性问题,说明回归模型的变量构建良好。最后从F检验的结果看,显著性P值均小于0.05,水平呈现显著性,拒绝回归系数为0的原假设,假设检验有效,即自变量与应变量存在显著的线性关系。因此,回归方程模型基本能满足要求,回归方程有效。回归方程为。

(6)

表3 多元线性回归结果与检验分析

一般,如果自变量的系数越大,说明应变量对该变量的变化就越敏感。从回归方程(6)式来看,对于降低吊装时结构的应力、局部变形来说,吊耳布置的均匀程度相比临时补强来的更有效一些;但对降低整体变形来说,有效的临时补强相比调整吊耳布置均匀度来说更有效。一般,均匀合理的布置吊耳相对临时补强来说成本来得更低,因此在吊装设计中,优先尽可能地均布吊耳位置,然后再考虑临时补强方式。如在应力满足条件的情况下,整体位移仍有较大的不满足时,可对较弱的框架进行临时补强,逐步增加补强范围,以降低成本。为尽量减少补强控制建造成本,同时使分段结构最大应力、整体最大变形和局部位移尽可能地都小,以提高安全余量,利用(6)构建线性规划数学模型如下。

目标函数

(7)

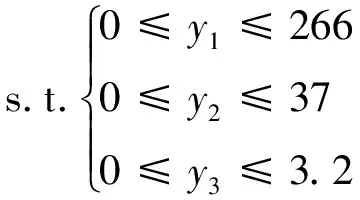
(8)

x1∈(1,2,3),x2∈(1,2,3)

利用分支界定数学规划法求解可得：当x1=3,x2=1时,即吊耳布置方式三、补强方式一(无需补强)是符合要求的最优吊装方案,也就是方案7。该方案仅通过优化吊耳布置而无需临时补强,即可满足应力、整体变形和局部变形的要求,同时可使这些值尽量的小,这对综合建造成本、结构安全性都是有利的。

4 结论

1)邮轮上建分段在吊装时须考虑舷侧开孔局部位移的评估,满足强度与整体位移要求的吊装方案,不一定满足局部位移的要求。

2)舷侧开孔局部位移评估时,纵向位移最小,占许用值不到10%,可忽略;横向位移次之,垂向位移最危险,为主控因素。

3)合理布置吊耳位置和进行临时加强均有利于控制吊装过程中的应力、整体位移和局部位移,但更合理的均布吊耳布置对降低应力、局部位移更为有效;合理的临时补强对降低整体位移更为有效。

4)吊耳的布置与临时补强无多重共线性问题,可以通过多元线性回归来构造吊装时应力与位移响应与这两个参数件的回归方程,通过对回归方程的数学规划求解,得到最优吊装方案。