基于扰动理论修正的桩-土接触面荷载传递模型及其应用

2024-02-26王友涛陈晓斌郝哲睿

地质与勘探 2024年1期

王友涛，谢康，陈晓斌，张飞，郝哲睿

（1.中铁一局，陕西西安 200082；2.中南大学土木工程学院，湖南长沙 410083）

0 引言

桩基础因其具有高承载力、高稳定性、低沉降以及施工快速便捷的特点，被广泛应用于新建构筑物基础（刘睦峰等，2006；秦鹏飞，2017；何忠明等，2019）。桩-土接触面作为土与结构物间受力与变形的传递媒介，其力学特性对土与结构间的相互作用具有重要影响，甚至往往成为土-结构体系的薄弱环节（沈保汉和王凤良，2010；贺凯，2019）。其中桩-土接触面是最为重要的一部分，正确理解复杂应力条件下桩土接触面的强度计算与变形机理是合理设计的重要前提（薛林华和李小青，2003；贾煜，2015）。因此研究土-结构接触面荷载传递模型及其在桩土界面中的应用具有重要的工程应用价值。

为了深入分析桩土接触面机理，亟需建立能合理反映接触界面复杂力学特性的本构模型（李海周，2016；齐艳霞等，2017；凌立鑫等，2023）。部分学者用双曲线模型来描述接触面的应力应变关系（刘树新等，2011；游强等，2011；吕鹏和刘建坤，2015），该模型的参数易于确定且具有明确的物理意义，因而得到了广泛的使用（范臻辉等，2006；游强和游猛，2011；张小玲等，2023）；部分学者通过分析双曲线模型参数与含水率、粗糙度和温度等影响因素间的关系，建立了考虑不同影响因素的接触面本构模型（Sato，1965；Desai et al.， 1985；Hryciw and Irsyam， 1993； Lings and Dietz， 2005；Chen et al.， 2015）。佐藤悟（1965）提出了一种桩-土荷载传递的理想弹塑性模型，该模型临界桩-土相对位移前侧摩阻力与相对位移呈线性关系，但该模拟由于表达式过于简单，导致其应用有限；Kraft and Ray（1981）基于实测资料，提出了桩-土荷载传递理想软化模型，该模型曲线由弹性段、软化段和塑性段三段组成。该模型表明桩侧摩阻力与土体的初始剪切模量呈线性关系，并且桩侧摩阻力与桩的影响区半径和桩径相关。与佐藤悟模型相比，该模型可以考虑侧阻软化，由于模型分段较多，临界点难以确定，计算复杂。之后，学者针对双曲线模型、抛物线模型以及弹塑性模型的不足提出对应的修正模型（曹汉志，1986；潘时声，1991；陈龙珠等，1994；何思明，1995；房卫民等，1999；辛公锋，2006）。同时，陈良致等（2016）也采用龚帕兹模型对不同温度条件下青藏冻土与玻璃钢接触面的应力应变关系进行预测，结果表明该模型仅能预测峰值前的应力应变关系，无法反应接触面剪切应力的软化过程。但是以上本构模型参数没涉及到材料状态对在变形过程中的影响，而考虑材料自身状态的“运动”理论模型，才具有较好的理论性和适用性。

为此，采用室内试验与理论相结合的方法，基于材料扰动理论，提出了修正的桩土接触面荷载传递模型，在此基础上建立能反映接触面复杂力学特性的本构模型。开展土-接触面的剪切试验，明确模型内部参数，进一步验证模型的合理性。结论有助于理解复杂应力条件下桩土接触面的强度与变形计算，也为锚杆、桩基础等相关结构设计提供参考。

1 土-结构接触面荷载模型

1.1 荷载分担模式

采用荷载传递法来表征出桩的荷载传递规律，桩-图相互作用的荷载传递法的计算模型如图1所示。在计算模型中，把桩离散为多个弹性桩单位，用独立的线性或非线性弹簧来描述每个桩单元与桩周图之间的相互作用，忽略桩单元之间的相互作用。

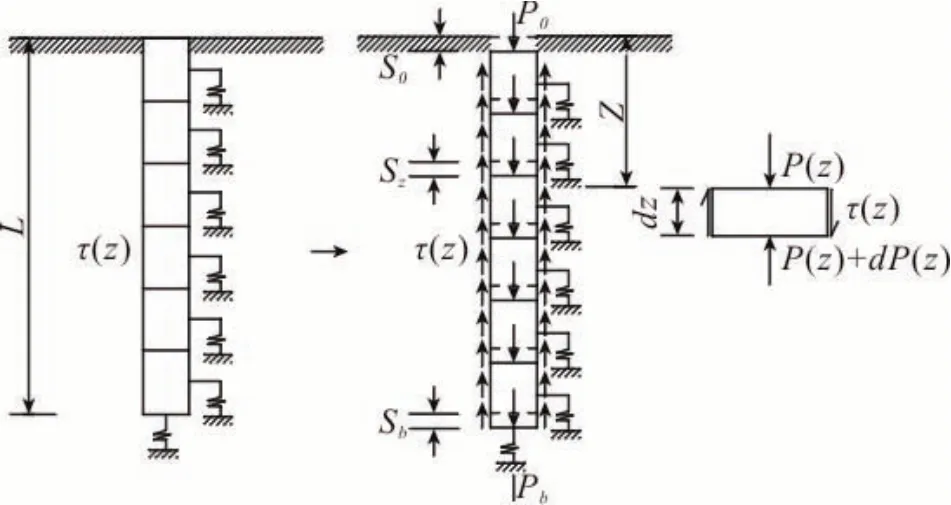
图1 荷载传递法的计算模型Fig.1 The calculation model of load transfer method

桩土接触面受力后，可认为接触面处于一种相对完整状态（RI）和完全调整状态（FA）随机组成的混合物（冯大阔和张建民，2018；赵雨朦等，2018）。扰动状态概念假定作用的荷载会引起两部分的相互作用，从而使材料或接触面单元发生扰动，即从最初的相对完整状态向最终的完全调整状态转变。根据扰动状态概念，由处于观测、相对完整和完全调整状态下力的平衡以及由应力定义的扰动函数。

全量式为：

式中，a，i，c分别表示RI和FA的响应；σaij为观测到的状态的总应力；σiij为RI部分的单元承担的应力；σcij为FA部分的单元承担应力。

考虑体积响应及基于孔隙比e的扰动函数De，观测应变张量的增量式为：

式中，εν为体积应变；为偏应变张量；δij为Kronecker符号；e0为初始孔隙比；e为孔隙与固体的体积之比。

在构建桩-土接触面荷载传递模型时认为接触面的单元是由相对完整状态（RI）和完全调整状态（FA）两种状态的单元的混合体，并做如下假定：1）在某一法向应力下，桩-土接触面剪切系数保持恒定；2）桩接触面的剪切应力由线弹性部分和塑性部分组成。

桩-土接触面的受荷过程由相对完整（RI）状态部分的单元和完全调整（FA）状态部分的单元共同作用，并以扰动因子D加权响应，见图2所示。

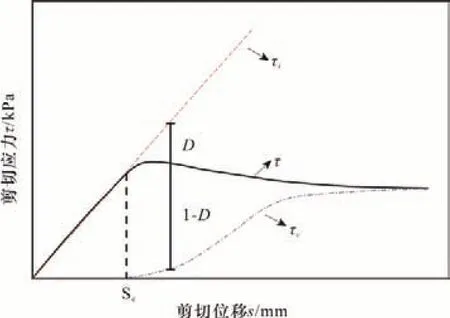
图2 扰动因子D的桩-土接触面应力-应变关系Fig.2 Stress-strain relationship of pile-soil interface with disturbance factor D

因此，桩-土接触面荷载传递函数表达式为：

式中，τ为桩侧（端）摩阻力；τi为桩-土接触面处于RI部分的单元应力；τc为桩-土接触面处于FA部分的单元应力；D为扰动因子。

1.2 荷载传递函数

（1）相对完整（RI）状态

根据桩-土接触面直剪试验结果，假定接触面单元中相对完整（RI）状态部分的抗剪强度服从线弹性理论。采用佐藤悟（1965）双折线模型的理想线弹性部分计算，其表达式为：

式中，k为桩-土接触面剪切系数；s为相对位移。

（2）完全调整（FA）状态

桩-土接触面单元完全调整（FA）状态部分的抗剪强度由接触面的残余强度承担，假定其服从理想塑性理论。在此，采用摩尔-库伦强度理论计算，其表达式为：

式中，c为桩-土接触面残余粘聚力；σn为法向应力；φ为残余内摩擦角。

1.3 扰动因子方程

由桩-土接触面荷载传递模型的函数表达式（7）可知，接触面是否发生扰动以接触面是否出现塑性位移为准，可定义扰动因子函数表达式为完全调整（FA）状态单元数量nf与总单元数量n之比：

式中，nf为桩-土接触面完全调整（FA）状态数量；n为接触面单元总数。

假定桩-土接触面单元强度服从Weibull分布，其分布密度表达式为：

式中，η、ξ为桩-土接触面扰动状态特性参数。

当桩-土接触面塑性位移为sf时，则接触面完全调整（FA）状态的单元数量为：

将式（7）、（8）带入式（9）可得扰动因子：

桩-土接触面塑性位移计算表达式为：

式中，s为接触面桩-土相对位移，se为弹性位移。

将式（9）、（10）带入式（11）可得桩-土接触面荷载传递模型函数的表达式为：

式中，k为桩-土接触面剪切系数；s为相对位移。τf为桩-土接触面残余应力；k、τf以及参数η、ξ由实测或试验的τ-s曲线确定。

为简化计算，将式（12）变换成线性方程：

式中：

根据实测或试验的τ-s曲线求得k、τf，进而求得x、y。将x、y带入式（14）即可求得a、b，进而得到参数η、ξ。

2 参数敏感性分析

由式（14）知，桩-土接触面荷载传递函数有4个影响参数，分别为k、τf、η、ξ。其中，主要影响参数有两个，分别为k、τf。为了分析桩-土接触面荷载传递函数主参数影响，使用Matlab软件编程计算各参数对荷载传递函数曲线形态的影响，对模型参数的特征进行分析。

修正的桩土接触面荷载传递模型的桩-土接触面荷载传递函数主参数影响分析结果见图3和图4所示。

图3 k变化影响下的τ-s曲线Fig.3 τ-s curves under the influence of k

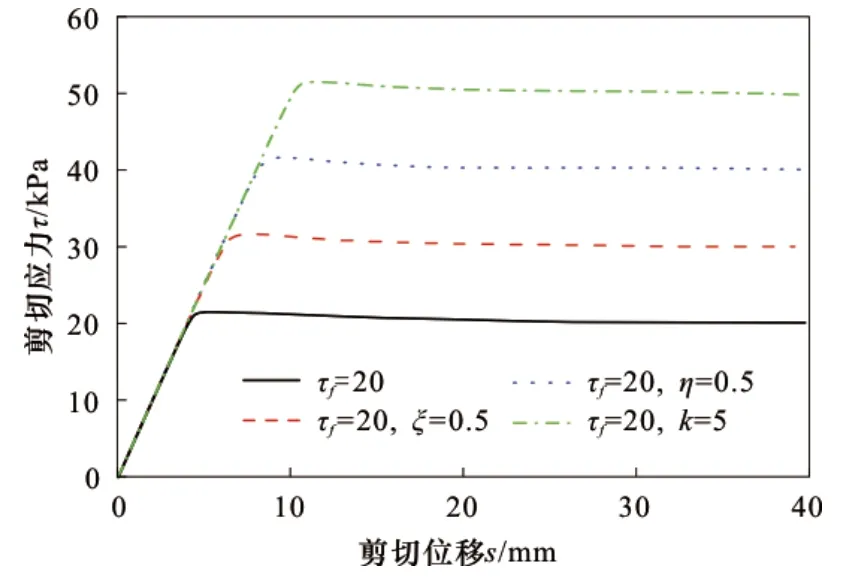
图4 τf变化影响下的τ-s曲线Fig.4 τ-s curve under the influence of τf

图3显示：荷载传递模型主要由两个阶段组成：线弹性阶段（0≤s≤se）和弹塑性阶段（s＞se）。

当剪切位移0≤s≤se，模型为线弹性阶段，剪切应力随位移的增加呈线性增加。同时，随着k的增加，剪切应力的增长速率随之增大，而与弹塑性阶段分界剪切位移逐渐减小；当剪切位移s＞se，接触面模型处于弹塑性阶段，此时剪切应力随剪切位移s的增加先增大后减小，最终趋于稳定。随着k的增大，接触面呈现出更为显著的应变软化特性，剪切应力峰值也逐渐显著上升，但最终残余剪切应力最终趋于接近τf。

提出桩-土接触面荷载传递模型的参数分析表明，参数k对模型τ-s曲线形态影响较大。在复杂应力条件下桩土接触面的强度与变形计算，锚杆、桩基础等相关结构设计时，应该对该参数进行试验确定。

图4显示：荷载传递模型τ-s曲线主要由两个阶段组成：当剪切位移0≤s≤se，处于线弹性阶段；当剪切位移s＞se，处于弹塑性阶段。参数τf对模型τ-s曲线形态没有影响。τf越大，两阶段分界点的位移se越大，接触面残余剪切应力越大，弹塑性阶段（s＞se）各τ-s曲线相互平行。

同样，不同的参数η、ξ变化，荷载传递模型τ-s曲线主要由两个阶段组成：当剪切位移0≤s≤se，处于线弹性阶段；当剪切位移s＞se，处于弹塑性阶段。参数η在描述桩-土接触面荷载传递特征时既能体现硬化特性又能体现软化特性。而参数ξ在描述接触面荷载传递特征时在弹性阶段τ-s曲线不发生变化，在弹塑性阶段，随着参数ξ的增大，接触面剪切应力峰值逐渐增大，但增加量较小，残余剪切应力几乎不变。

3 荷载传递模型验证

为验证荷载传递模型，更深刻了解桩-土接触面上的受力变形机理、剪切破坏发展、荷载传递过程，开展了桩-土接触面的大型直剪试验。

3.1 试验方法

接触面直剪试验的桩周土选取褐红色粉质黏土和粉细砂，基本物理力学参数，见表1所示。

表1 土体基本物理力学参数Table 1 Basic physical and mechanical parameters of soil

为真实反映桩-土接触面的摩擦状态，采用大型直剪仪开展桩-土接触面试验（见图5所示），剪切盒大小为500 mm×500 mm×150 mm。

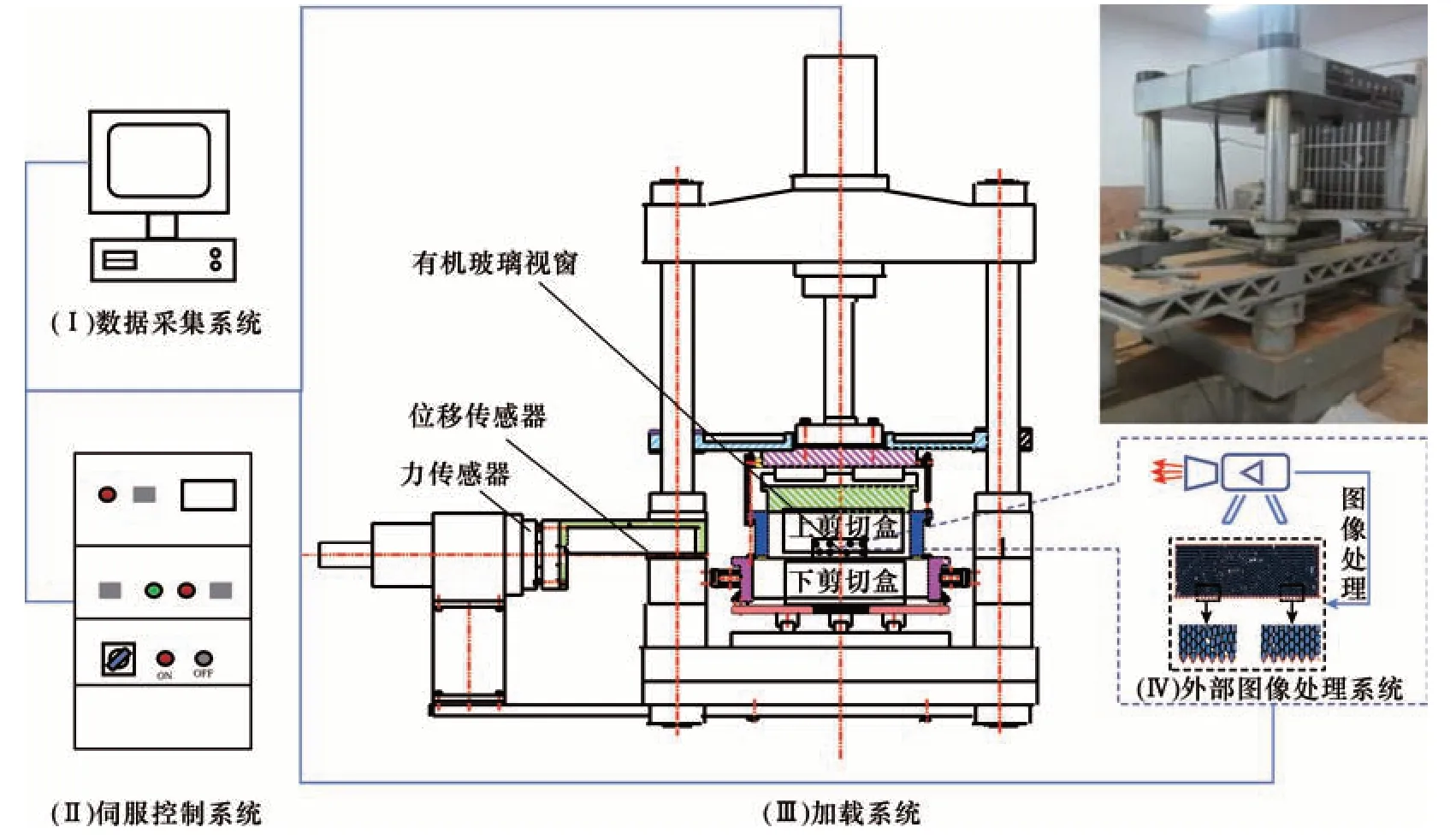
图5 大型剪切试验仪Fig.5 Large shear test equipment

依据《桩基工程手册》，沿海地区及其他地层条件不好的地区，桩的深度在50 m左右。不考虑地下水作用时，依据《建筑基坑工程技术规范》K0（静止土压力系数）取值：为塑软黏性土时，取0.5～0.6；为砂土时，取0.4～0.5。根据本试验的土样，因此K0值取0.5。深度取50 m时，取试验土样的最大值为18.1 kN/m3，计算得压力为425.5 kPa。

试验中，选择的100 kPa法向压力，可以考虑小于30 m长的桩实际工作状态；所选择的200 kPa，可以考虑小于50 m长的桩实际工作状态；所选择的400 kPa法向压力，目的在于探索较高应力状态下的适应性，以便于拓展模型的应用范围。参考之前学者的研究，桩-土接触面直剪试验剪切速率取1 mm/min。

3.2 荷载模型验证

将试验结果按式（12）可求得桩-土接触面荷载传递模型中的参数，见表2所示。结果显示：随着桩-土接触面法向应力的增大，接触面的抗剪系数及残余剪切应力呈增加的趋势。

表2 接触面荷载传递模型参数Table 2 Parameters of contact surface load transfer model

试验与模型计算τ-s曲线的对比见图6所示。

图6 试验τ-s曲线与模型计算τ-s曲线Fig.6 Experimental τ-s curves and model calculated τ-s curves

图6显示：模型的理论计算结果与试验结果吻合很好，能够较好地反映桩-土接触面的应变软化特性。

4 现场应用分析

为了扩展到其他类型桩周土，采用已有试验数据（王卫东等，2011），进一步验证提出的荷载传递模型。据吕鹏和刘建坤（2015）研究相关的试桩SYZA02桩径为1 m，桩长为88 m，有效桩长为63 m，为桩侧桩端联合后注浆。土-结构接触面荷载模型的基本参数如表3所示。

表3 现场的桩-土荷载传递模型参数Table 3 Parameters of in-situ pile-soil surface load transfer model

表3数据显示，土层特性对桩-土荷载传递模型各参数有较大的影响。桩-土接触面剪切系数k在粉质黏土较小，在粉质砂土中较大，细粉砂和砂质粉土夹粉砂次之，说明土层力学特性越好，剪切系数k值越大。参数η与桩-土接触面的软硬化特性相关，η值越小，软化程度越弱。

选取桩身位置分别在25、35、50、65 m处桩段的桩侧τ-s实测值与计算值进行对比。图7为桩侧τ-s实测与理论值曲线。

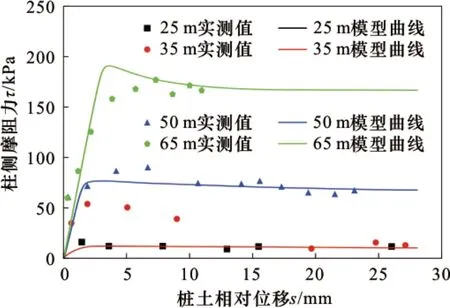
图7 现场桩侧τ-s 实测与理论值曲线Fig.7 In-situ τ-s curves and model calculated τ-s curves

图7显示，理论结果与实测结果吻合较好，可以反映桩-土接触面的软硬化特性，说明提出的桩-土荷载传递模型能够较好的描述桩-土之间的荷载传递规律，同时也验证了模型的合理性。

5 结论

引入扰动状态概念（DSC），建立了修正的桩土接触面荷载传递模型。通过直剪试验对模型的合理性进行验证。该模型能够反映桩侧应变软化及硬化特性，具有较好的理论性和广泛的适用性。提出桩-土接触面荷载传递模型的参数分析表明，参数k、η对模型τ-s曲线形态影响较大。在复杂应力条件下桩土接触面的强度与变形计算时，应对该参数进行试验确定。所得研究结论有助于理解复杂应力条件下桩土接触面的强度与变形计算，亦可为锚杆、桩基础等结构设计提供参考。

［附中文参考文献］

曹汉志.1986.桩的轴向荷载传递及荷载-沉降曲线的数值计算方法［J］.岩土工程学报， 8（6）：37-49.

陈良致，温智，董盛时，俞祁浩，薛珂，张明礼.2016.青藏冻结粉土与玻璃钢接触面本构模型研究［J］.冰川冻土，38（2）：402-408.

陈龙珠，梁国钱，朱金颖，葛炜.1994.桩轴向荷载-沉降曲线的一种解析算法［J］.岩土工程学报，16（6）：30-38.

范臻辉，肖宏彬，王永和.2006.膨胀土与结构物接触面的力学特性试验研究［J］.中国铁道科学，1（5）：13-16.

房卫民，赵明华，苏检来.1999.由沉降量控制桩竖向极限承载力的分析［J］.公路工程，1（2）：25-27.

冯大阔，张建民.2012.粗粒土与结构接触面静动力学特性的大型单剪试验研究［J］.岩土工程学报，34（7）：1201-1208.

贺凯.2019.现浇螺杆桩在高速铁路站场软基处理中的应用［J］.人民交通， 22（7）：78-80.

何思明.1995.基于荷载传递函数法的单桩沉降计算［J］.四川建筑科学研究，2（2）：44-45.

何忠明，彭生辉，范电华，王保林.2019.桂三高速公路高架桥右侧边坡稳定性时空演变规律分析［J］.地质与勘探，55（5）：1294-1301.

贾煜，宋福贵，王炳龙，杨龙才.2015.基于改进荷载传递法计算降水引起的基桩沉降［J］.岩土力学，36（1）：68-82.

李海周.2016.杆灌注桩的受力机理分析［D］.邯郸：河北工程大学：28-29.