粒子群算法压缩资源传递中重叠活动的工期

沈健SHEN Jian；王可欣WANG Ke-xin

（江西科技师范大学土木工程学院，南昌 330013）

0 引言

工程活动工期，常用关键线路法结合不同方法缩短工期[1]，或将单项目和启发式算法结合起来提出工期进度优化方案，刘军建立工期—成本优化模型，采用粒子群智能算法解决项目工期—成本优化问题[2]。传统紧前工作结束再进行下一活动的搭接方式，压缩工期十分有限，将活动重叠能更有效率的减少工期。重叠活动中下游活动提前进行，上游下游活动信息和资源传递时间发生变化，有概率造成下游活动返工[3]。于静等人提出活动重叠导致下游活动返工时间的二项分布概率模型并用遗传算法进行优化[4]，张剑研究重叠活动仿真算法[5]，讨论信息传递造成返工对工期的影响。本文研究重叠活动资源传递的工期压缩问题，主要在于：①分析重叠活动中资源的调度，分析资源调度对上游和下游工作的影响和对影响的敏感度，建立工作延长时间模型。②粒子群算法求解工期。③基于算例验证模型有效性。

1 问题描述

活动A 和活动B 重叠进行，如图1 所示，活动A 工作时间为di，活动B 工作时间为dj；重叠部分Lag；上游活动A 进行的同时下游活动B 开始工作，导致上游活动在某一时刻（ti）传递部分资源到下游活动，上游的资源减少，导致上游工作工期时间相应的延长。资源传递造成的活动时间延长用TT 表示。

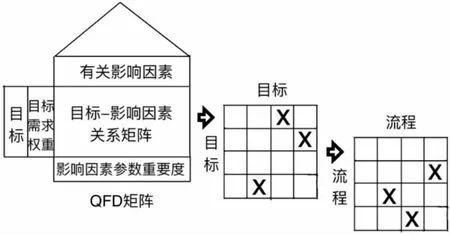
图1 DSM-QFD 多级瀑布模型

本文基于以下假设开展：①活动之间的资源传递只能从上游活动到下游活动，即资源传递是单向的，重叠搭接的资源传递导致的活动工期延长只会产生在上游活动中。②上游活动在下游活动开始之前开始，在下游活动结束之前结束，保证活动和活动之间的逻辑不变。③活动和活动之间的资源传递不需要耗费时间。

2 模型建立

2.1 DSM-QFD 模型建立

DSM 矩阵可直观地对复杂项目进行分析，但无法跨领域表示元素依赖关系，矩阵中非对角线的“x”表示上下游之间的资源依赖，上三角的标记表示下游活动接收到上游活动分享资源时占下游活动的工期时间比例，下三角的标记表示上游活动在传递资源时上游工作完成比率。QDF矩阵可把产品目标和需求体现在矩阵中，但不能分析同一领域元素关系。将QDF 和DSM 矩阵结合，得到从QFD 矩阵开始按不同领域因素的相关性层层推导DSM 的模式，逐级推导得到工序流程之间的关系，即流程DSM 矩阵，并以此来计算工程工期。具体原理如图1 所示。

通过专家打分的方法确定目标要求要素的重要程度，由层次分析法计算出要素的权重。建立目标需求要素和目标影响要素的QFD 质量屋矩阵，如图2。QFD 矩阵中，目标需求要素i 对目标影响要素k 的影响为正向影响则为正，负向影响则为负。

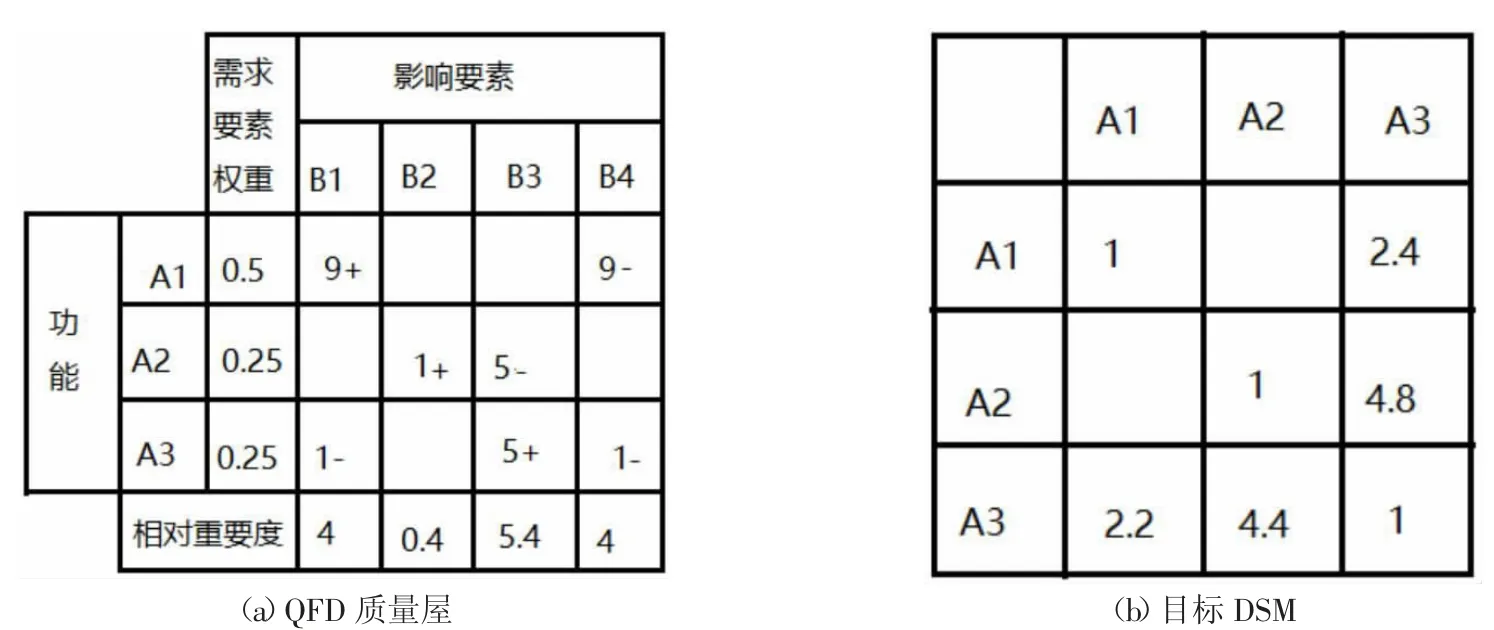
图2 由QFD 矩阵推到DSM 矩阵

各个目标影响要素的相对重要程度ωk计算公式（1）为：

i=1，2，…，m，k=1，2，…，k；Fi——目标需求要素的权重；QDF（i，k）——QFD 矩阵中，目标需求要素和目标影响要素之间的依赖度；m——目标需求要素的数量；K——目标影响要素的数量。

利用DSM-QFD 多级瀑布模型，利用QFD 矩阵计算目标的DSM 矩阵，QFD 矩阵中数值表述影响要素对目标要素的影响大小，本文只考虑相关元素成反向关系时来计算，这样的元素之间是相互依赖相互制约的，活动目标要素DSM 中元素的依赖强度用DSM1（i，j）表示，可以公式（2）计算：

K——目标影响要素的数量。

最后利用DSM-QFD 多级瀑布模型，从目标DSM 矩阵转换成流程DSM 矩阵。刘志林[6]介绍了一种插入多领域矩阵MDM 从一项DSM 矩阵转化为另一项DSM 矩阵的方法，计算公式如（3）：

m 为需求目标个数；DMM（I，i）为所求DSM2 矩阵元素（I，J）对应的第I 行非零数；DMM（J，j）为所求DSM2 矩阵元素（I，J）对应的第J 行非零数。

关注目标需求要素和目标影响要素互相影响，利用DSM-QFD 多级瀑布模型计算DSM 矩阵。由QFD-DSM 多级瀑布模型的算式（2）、（3）可以逐级得到资源传递后上游工作可能发生的工期延长情况的程度，即工期延长程度（RI）。活动工期延长概率（RP）由层次分析法和算式（2）直接计算得出。

2.2 重叠活动的资源传递调度模型

引起下游活动返工的主要原因是上游活动将资源分给下游活动导致上游活动的资源减少的敏感度，如图3 所示。上游在活动的某一随机时刻tk 将部分资源传递给下游活动，传递资源的时间tk 越早，上游活动资源变少的时间越长，下游活动占用资源的时间就越长，可能造成的上游活动工期延长的情况风险就越大，反之上游活动传递给下游活动资源的时间tk 越靠后，造成上游活动工期延长的风险就越小。上游活动对传递资源给下游活动的敏感度是随时间而递减的减函数。而活动的重叠时间和上游传递时间共同影响上游工作可能延长工期的敏感度，重叠时间越长，资源重合时间越长，敏感度越高。由此可得。

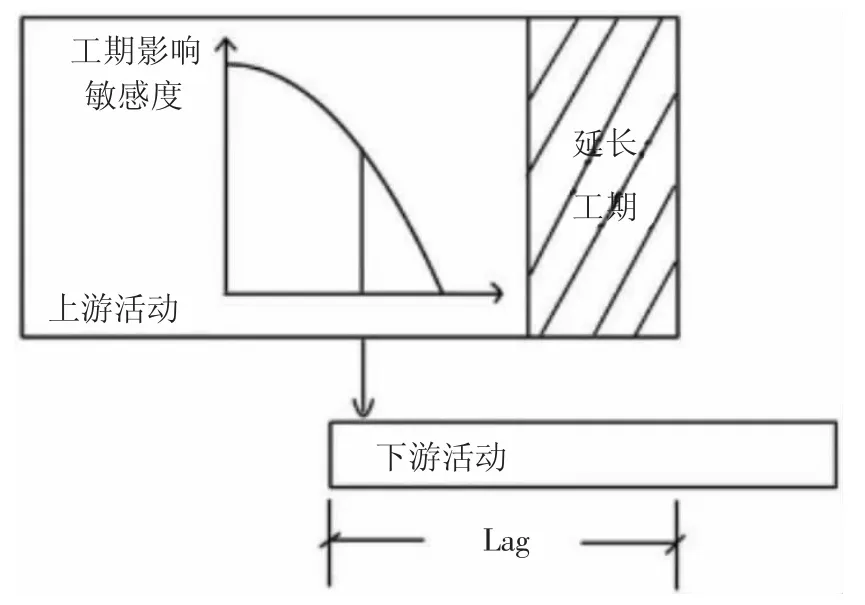
图3 上游活动工期影响敏感度

下游活动敏感度计算公式为：

r（tj）为在ti 时刻上游活动传递资源给下游活动时的敏感度；Lag 为活动重叠时间。

上下游活动之间重叠时间Lag 为：

IOI 为资源传递时间矩阵，表示上游活动向下游活动传递资源时上游活动已完成的比例；IRI 为资源接收时间矩阵，表示上游活动向下游活动传递资源时下游活动已完成的比例。

根据上面的式子，可以发现活动的重叠时间和上游传递时间共同影响上游工作可能延长工期的敏感度，重叠时间越长，资源重合时间越长，敏感度越高。以此可以得到活动返工风险发生的概率：

RP 为活动可以出现活动工期延长的概率矩阵。

下游活动返工时间为：

RI 表示活动工期延长程度矩阵。

总工期工期：

N 为活动个数。

逻辑关系约束：

3 实例分析

哈尔滨工业大学要进行多个教学楼建设，以其中一个实验教学楼建设工程为例，对以上理论进行实例分析。因该工程较大，故以实验教学楼基础部分为主。基础部分施工工序较少，主要包括以下几个工序：A 基础钢筋安装，B基础装模，C 基础浇砼，D 承台装模，浇砼，E 承台脱模养护，G 基础混凝土养护，H 拆模及清理基底，I 基础土方回填夯实，各活动工期和网络计划图如图4 所示，工期为55 天。

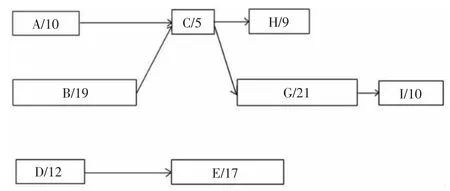
图4 工程网络计划图

目标需求要素分别为：A1 高工程建设质量、A2 安全生产、A3 资源均衡、A4 低工程成本、A5 环境友好、A6 标准化、A7 符合市场要求、A8 工程工期合理。通过给专家发送调查问卷，层次分析法得出目标需求要素的权重为[0.063，0.043，0.14，0.249，0.099，0.028，0.019，0.359]；目标影响要素为：B1 设计因素、B2 施工人员因素、B3 建筑材料、B4 安全管理、B5 资源供给量。根据专家调查问卷和QFD 质量屋得出需求影响要素的相对重要程度为[0.371，1.462，1.42，0.682，1.593]。

用QFD-DSM 多级瀑布模型得出的RI 矩阵和RP 矩阵如图5、图6 所示。

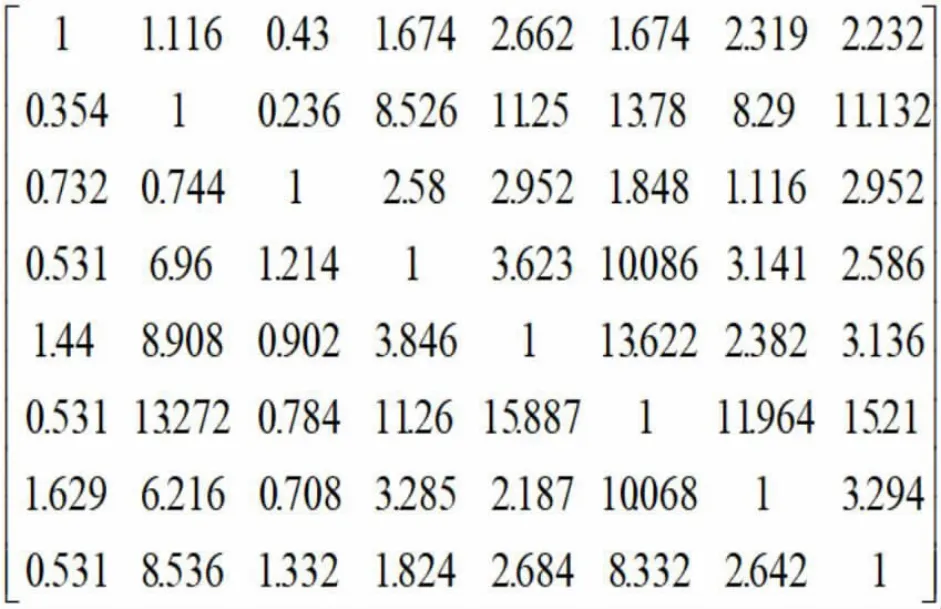
图5 工期延长程度RI 矩阵图

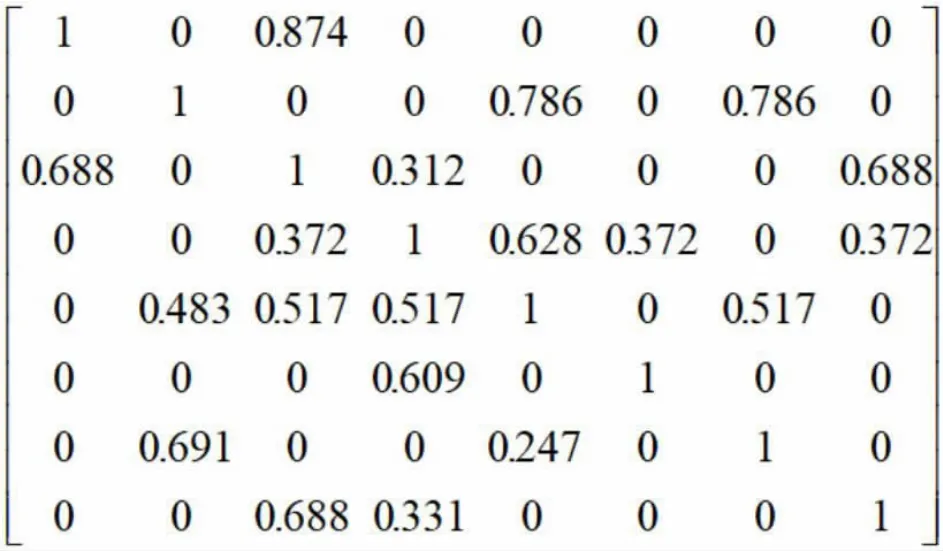
图6 工期延长概率矩阵RP 矩阵

利用公式（4）-（8）计算并用粒子群算法解出工期最优解，如图7 所示，工期最优解52.5 天，缩短2.5 天。

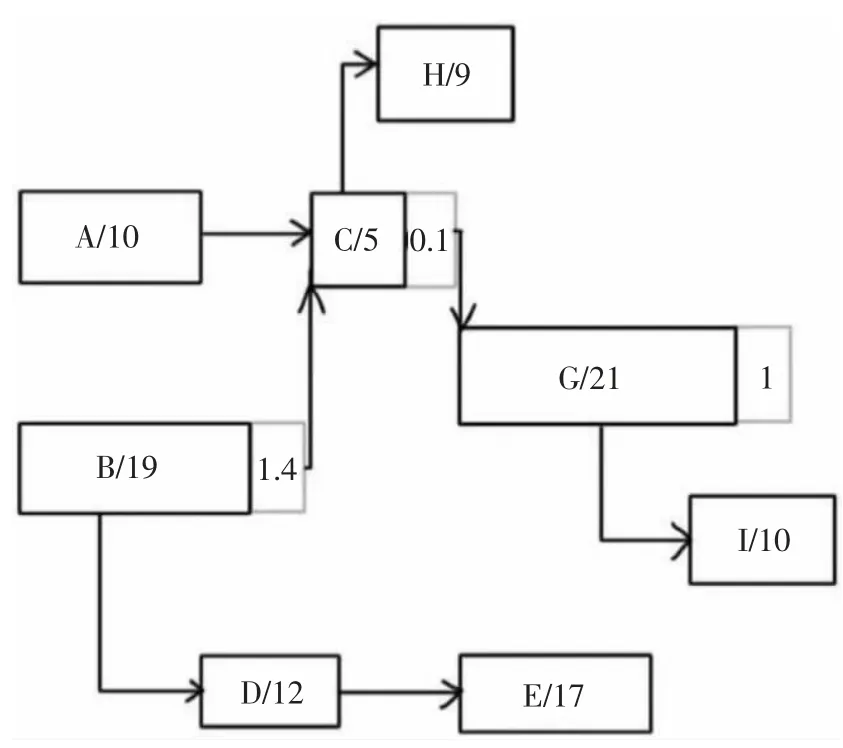
图7 优化后工程网络计划图

4 结论

本文建立了重叠活动中上游向下游传递资源导致上游延长活动时间的重叠活动的那个工期模型，在模型中引入了资源传递时间与上游活动敏感度的概念；引入了DSM-QFD 模型，多级瀑布模型计算出不同领域的DSM 矩阵，以此计算工程工期；本文用实际算例的计算验证了本文模型的有效性，并利用粒子群算法计算出了工期最优解。