特高压电网不等高差短导线的受力性能*

2024-02-24信珂刘欣悦王乐天马会环金耕涛

中山大学学报(自然科学版)(中英文) 2024年1期

信珂，刘欣悦，王乐天，马会环，金耕涛

1.山东电力工程咨询院有限公司，山东济南 250013

2.哈尔滨工业大学土木工程学院，黑龙江哈尔滨 150090

3.中山大学土木工程学院 / 南方海洋科学与工程广东省实验室（珠海），广东珠海 519082

近年来，随着我国远距离输电线路的电压突破升高，推动了多个科技领域的快速发展（张原，2019）。特高压输电线路是指电压超过1 000 kⅤ的交流输电线路，或是电压超过800 kⅤ的直流输电线路（李江明等，2019）。特高压电网相对于传统电网在远距离输电效率上具有显著优势，使得诸如水力发电、风力发电等电力资源通过特高压电网技术突破地理位置的限制。不断发展的特高压电网将成为中国电力系统的输电大动脉，社会各界对其安全性也比较关注（谷琛等，2020）。在特高压电网的输电营运期，因现行的导线受力设计方法与导线实际受力情况不匹配，造成了一些生产安全事故。目前的导线受力设计方法未考虑导线自身刚度，而特高压输电工程中实际所用的导线材料通常是特殊类型的导线，其同时具备一定的柔韧性和一定程度刚性特性，并且设备之间的导线连接距离很短，不符合目前的设计要求（孙宏彪，2020）。近年来，不同学者已经对输电短导线开展了系列研究，但对较短导线的力学计算模型研究仍有待深入（于运涛，2020）。

对于导线承受力的特性研究相对较少，当前的主要研究手段包括试验观察和有限元模拟分析。一些研究者提出了针对特高压输电线路所用的捻制导线结构最大弯曲刚度EⅠmax和最小弯曲刚度EⅠmin的概念。当导线整个截面符合平截面假定时，导线具有最大弯曲刚度EⅠmax，若仅有构成导线的各股线符合平截面假定时，此状态下导线具有最小弯曲刚度EⅠmin，各股线的变形不会相互影响（Papailiou，1997）。实际工程中，导线的实际弯曲刚度EⅠ大于EⅠmin而小于EⅠmax，处于二者之间。根据这些观点，实际上导线的弯曲刚度是位于最大弯曲刚度EⅠmax和最小弯曲刚度EⅠmin之间的，这取决于实际导线受到的轴向力数值和弯曲程度，同时，导线弯曲刚度的变化机制也与股线间的相对滑移程度相关。有研究人员通过测量JLHN58K-1600 导线在各种安装间隔下末端的束缚力和悬挂高度来探索这个问题（万建成，2010）。有学者通过限元分析方法，完善了股线之间发生相对滑动的判断依据，从只考虑导线曲率这个单一指标转换为同时考虑曲率、外荷载随时间的变化率及各股线间的摩擦力等指标，以提升计算的准确性（Foti et al.， 2016）。研究者在建模时把导线视为链式梁模型，取EⅠmin作为其弯曲刚度，研究结论与万建成等学者的结论基本吻合，同时通过开展试验研究证明了该方法的有效性（何畅等，2018）。

在绞线精细化有限元模型中，如何考虑股线间相互摩擦存在争议，学术界对此存在不同观点。研究者基于弹性绞线的二维截面模型，探讨了无摩擦力绞丝之间的接触作用（Argatov，2011）。研究发现，当螺旋角度小于15°时，接触效应对绞线受力反应的影响微乎其微；然而，对于大于25°螺旋角的绞线，当绞线受到外力作用时，绞丝之间接触力效应显著增加。通过参数化的数值仿真模型研究四层导线的力学特性并与试验结果对比，发现该数值模拟方法与试验结果的相对误差仅为13.5%，展现出了良好的模拟效果（Kmet et al.，2013）。有研究者通过一种半解析方法来确定导线中心线与外围绞线的触碰力（Chen et al.，2016）。此方法通过快速傅立叶变换算法和离散卷积算法开展离散单元相互作用力的计算，研究表明这种算法能够在特定情况下获得接近于有限元模拟的结果。有文献提出新的观点，把绞线在承受单轴扭矩作用或轴向拉伸作用时的响应划分为接触形变及无摩擦变形两类情况，并且在此约束下给出理论预测值（Zhang et al.，2019）。有研究指出，是否有摩擦过程对绞丝应力的影响非常有限。对四分裂导线上的覆冰开展研究，研究覆冰在直流融冰时的脱落过程，结果显示：采用直流融冰方法时，脱冰瞬间导线的跳跃高度比正常脱冰的跳跃高度小，导线脱冰瞬间的跳跃高度和瞬时张力随着直流电流的增加而减小（祝贺等，2023）。有学者对扩径导线的受力特性开展了研究，考虑了环境风速、导线直径等因素的影响，结果证明扩径导线表面的最大水滴碰撞系数随着直径的增大而减小（吴海涛等，2023）。研究人员建立了反映导线自由扭转覆冰动态过程的仿真分析模型，证明了导线扭转角度和单位覆冰质量沿单导线中心点对称分布（杨国林等，2023）。

现有的导线受力分析方法与实际应用场景中的实际受力特性还有差距，尚未建立可对实际特高压导线受力性能开展准确计算的设计方法。针对此问题，论文建立了特高压变电站内短导线计算有限元模型，针对不同高度差下的导线端部受力特性开展分析。考虑导线连接距离变化、高度变化和类型变化等，计算导线末端受到的约束力和力矩，获得影响特高压短导线端部受力特性的关键参数，在此基础上，构建可供实际工程计算参考的经验公式，以便更好地指导工程实践。

1 导线计算长度及风荷载确定

当导线两端等高差时，适合采用统一的风速值来进行分析。而当导线两端存在不同高差时，两悬挂点的垂直方向距离较大（见图1），由于随着海拔的上升空气风速随之增强，此时需充分考量到气流与地面的相对位置关系。为了保证分析结果的精确度和提高计算运算效能，参考信珂等（2021）研究工作中对环境风荷载的处理，设定导线底部的高程为4 m，取导线两端所处高度范围内的平均风速来分析。根据《电力工程电气设计手册（电气一次部分）》中的内容，平均风速Uf为

图1 不等高差情况Fig.1 The situation of height difference

式中Z0为导线上挂线点的距地高度（m）；Ub为平均风速最大值（m/s）；Z为基本距离地面高度（m）；Zb是指导线的最大地面距离（m）；α为与场地条件相关的参数，这里取0.22。

参考实际工程中导线的参数可知，上挂线点所用的线夹角度为0°，因此电缆上挂点以竖直向下的方式安装，而下挂线点可选择角度为0°或60°的线夹。以60°的线夹为例，如图2 所示，数值建模分析时，以上挂线点作为平面坐标系的原点，以指向下挂线点的垂直方向作为y轴的正方向，导线两个端部间的水平间距l变大的方向作为x轴的正方向，建立平面坐标系。

图2 找形示意图（线夹角度为60°）Fig.2 Shape finding diagram (clamp angle is 60°)

根据上述平面坐标系，导线的形状方程选用三次函数进行拟合

式中参数a、b是待定系数。

考虑到所连接线夹的使用特性，假设导线两悬挂点之间的高差为h=x0，悬挂点间距l=y0，则可根据以下方程求得导线的长度

式中y0与所采用的线夹种类有关。当采用60°的线夹角度时，得到

先确定拟合的导线形状函数，然后再利用线积分计算所需的导线连接长度

根据这个数值进一步确定导线长度的冗余值

此外，当下挂线点的线夹角度为0°时，采用该方法会导致y'0→∞，形状方程中的系数难以求解得到。因此，需要采取一种新策略——将导线在实际空间中的位置旋转45°后再求解，如图3所示。图3中，红色加粗线段代表了要求解的导线曲线。

图3 设备线夹角度为0°时的处理方法Fig.3 Handling methods for device clamps (angle is 0°)

由导线上下挂线点的平面坐标，可构建一个矩形，将导线装配完成后在平面坐标系中转动45°，使该矩形的一个角点（非导线悬挂点）作为坐标系原点，假设地球引力方向为y=-x方向指向第四象限的方向建立坐标系。在该坐标体系中定义了导线的形状函数

其中参数a、b、c、d代表待定系数。

根据两个挂线点处的线夹角度及平面位置，可以得到方程的边界条件的特定值，此时可得与上文类似的系数方程组

利用上述方程组确定的三次函数在导线两个挂线点范围内进行线积分，便可计算出该连接状态下所需的导线长度

式中的积分上、下限值分别为

2 60°线夹短导线端部受力分析

导线两端不等高差时，在环境风荷载和“端部安装固定”的作用下，将导致上、下挂线点处各存在6 个自由度上的约束反力Fx、Fy、Fz、Mx、My、Mz。Fix中的角标1 指上挂线点位置，角标2 则是指下挂线点位置（i= 1，2），g是代表地球的重力加速度。约束反力和约束力矩的平衡都需被考虑

只需对其中的3个约束反力分析即可掌握其余约束力随着高度差异而变化。实际上，在实际工程中，导线上挂线点的扭矩Ty较其余两种力矩（Mx、My）在数量级上小2 个等级或更多，所以为简化计算，分析中不考虑该扭矩。当研究不同的高度差距导线时，需要关注的变量包含Fx、F1y、F1z/F2z、M1x、M1z、M2x、M2y和M2z。先对设备夹线角度为60° 时的情况分析，其有限元模拟结果见图4。

图4 Fx随高差h变化Fig.4 Fx changes with height difference h

由图4 可知，当导线两端的高度差h超过某个特定值后，水平作用力Fx趋于稳定。然而，导线两端水平间距不同时，其所对应的“临界差距值”也不同。

深入研究表明，Fx趋于稳定后的高差h与间距l基本满足以下关系

研究发现，采用设备线夹的角度为60°时，底部夹角过小会出现导线“反弯”的特殊情况，导致端子的受力增加；相反地，若底角夹角较大，那么端子的受力就会相对减少并保持稳定。“反弯”状态的出现导致水平力Fx的波动且受力比稳定状态下的大。但是，随着导线端子距离的增长，不稳定状态会减轻甚至完全消退。Fx随间距l变化关系如图5所示。

图5 Fx随间距l变化Fig.5 Fx changes with spacing l

根据分析结果拟合的函数为

式中斜率kx是导线在x方向上的刚度，根据拟合结果取80.21 N/m；此时截距F0，x是当端子间隔为0时，下悬挂点采用了设备线夹角度为60°时x方向上的力，根据拟合结果取-33.23 N。

为了验证该拟合公式在不同高度差情况下的精确度，开展导线端子在不同高差条件下的数值模拟分析，用数值模拟结果与拟合公式计算结果对比分析，并计算两种方法的相对误差。研究发现，数值模拟结果与拟合公式结果的误差基本在-15%～5%之间，大部分结果的相差-10%～5%范围内，该误差范围是可接受的。且由于大部分误差为负值说明了该拟合公式计算的结果偏安全的。

数值模拟还分析了导线上悬挂点垂直方向的力F1y，数值计算结果见图6。

图6 F1y随高差h变化Fig.6 F1y changes with height difference h

根据图中的数值分析结果拟合曲线，得到拟合曲线的表达式为

式中斜率k1y是导线在y方向上的刚度，根据拟合结果取90.24 N/m；截距F0，1y是当端子高差为0 时，上悬挂点受到y方向上的力，根据拟合结果取-64.2 N。

基于同样的分析方法，开展了导线在z轴上的力学分析。由图7可得，随着导线两个端子高差的增加，F1z(F2z)呈线性上升趋势；随着导线端子距离的增加，F1z(F2z)随之增加，但是增幅较小。此外，上悬挂点受到z向的力始终大于下悬挂点。研究发现，参数F1z/F2z处于大于1 的特定区间上。因为参数F1z/F2z变动的区间较小，计算其均值以后，可以取1.12 作为参考值以确保安全性。所以，F1z、F2z的计算方法为

图7 F1y随高差h变化（稳定值）Fig.7 F1y changes with height difference h (stable value)

其中系数1.1 是根据工程实际需求而增设的安全系数。为了防止由于数据偏差导致的安全冗余度不够，将荷载增大10%以便使得计算结果更加安全。

分析导线的设备线夹角度为60°时，端子所受弯矩M1x、M1z、M2x、M2y和M2z的结果见图8。不但研究短导线端部弯矩随高差的变化特征，同时也分析了不同水平间距对导线弯矩的影响。对于较大的水平间距工况下，其所取的高差范围也相应增大。

图8 z方向端部受力随高差变化Fig.8 The force at the end of the z-direction varies with the height difference h

图9 可知，M1x、M2x和M2y这3 个参数的变化趋势随高差呈线性变化特征，受到水平距离的影响不大。基于此，用前述方法进行拟合。对于特定的间隔，弯矩M1z随着导线高度差达到一定值后就几乎保持恒定。弯矩M2z同时受到水平间隔距离和高度差异的双重影响，若仅对同一间距分析，弯矩M2z随着高差的变化趋势近似于线性变化。此外，不同导线悬挂点间距下得出的M2z-h曲线基本保持平行。

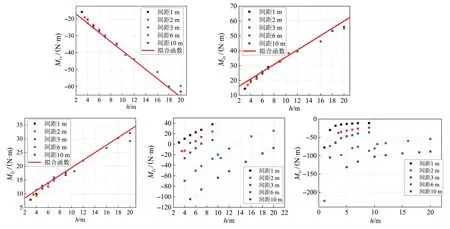
图9 60°设备线夹弯矩计算结果Fig.9 Calculation results of bending moment of 60° equipment clamp

基于上述参数分析结果，可总结出弯矩计算公式（14），从实际工程的应用角度考虑，为使结果偏安全特将拟合结果放大5%。

其中

弯矩M1z稳定后受高差变化的影响不大，如图10所示。

图10 弯矩与间距变化关系Fig.10 Relationship between bending moment and spacing variation

由图10 可知，M1z随水平间距呈负相关关系。因此，该弯矩的计算公式为

其中k1z=-9.06 N，M0，1z=-3.84 N·m.

依据M2z受水平距离和高度差异的变化特性，对不同水平间距下的模拟结果拟合，得到拟合方程的斜率和截距，具体结果见表1。

表1 不同水平间距下弯矩M2z计算公式的拟合参数Table 1 Fitting parameters of the calculation formula of bending moment M2z at different horizontal spacing

研究发现，斜率受水平间距变化的影响较小，拟合公式中取斜率平均值。截距与水平间距呈线性变化关系，可得弯矩M2z的计算公式

其中k2zh=6.38 N，k2zl=12.57 N，M0，2z=-7.89 N·m 。

3 不同型号导线受力性能分析

为比较各种类型导线的受力特性，对刚度最高的NRLH58J-1440 型导线开展研究。通过以下几种不同间距和不同高差的应用场景为例，分析该类型导线端部在空间分布状态下所受的约束作用特征，具体工况序号见图11。

图11 NRLH58J-1440型导线的空间布局特征及工况编号Fig.11 Spatial distribution characteristics and model number of the NRLH58J-1440 transmission lines

导线端子在z方向所受力的结果见表2，表2中详细列出了F1z和F2z的计算值。导线端子其他几个自由度上的力及力矩结果见表3，表3 中的参数是在相同工况下，其他自由度上约束力与LGJ-500/45 型导线端子的约束力的比值。

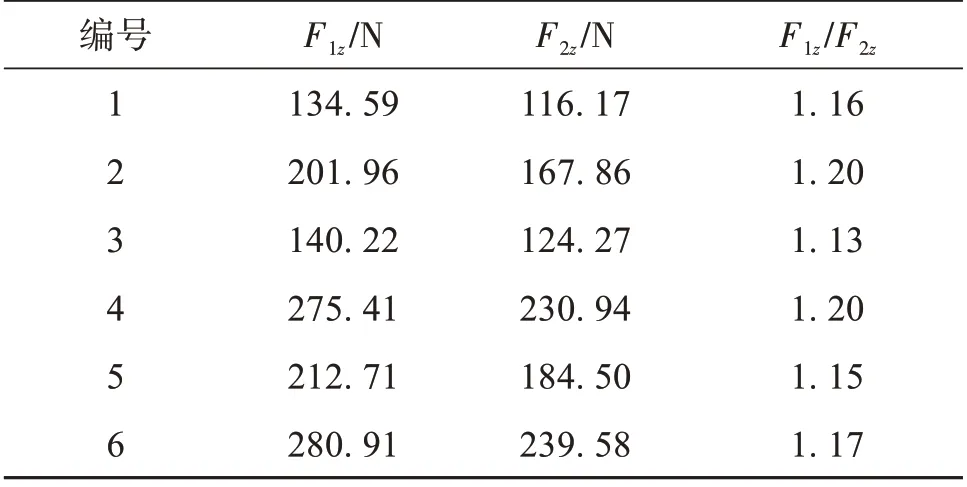
表2 z方向导线端子所受的约束作用Table 2 Constraints on wire ends in the z direction

表3 其他方向所受的约束作用Table 3 Constraints on wire ends in other directions

由表3 可知，F1z/F2z的变化相对较小，均值为1.16。与LGJ-500/45 型导线的计算结果1.12 相比，两者差异较小。基于前述分析过程中荷载放大了10%，因此导线两个端子在z方向所受力的比值可取1.12～1.16 中的任意值。其他分析方法与前述一致。

由表3 可知，在不同工况下导线端子所受的F1x与M2z计算值变动较大。其他的作用力或力矩的计算结果在不同工况组下较稳定，所以采用这些力学参数的均值进行分析。F1x随着水平间隔距离的增加而增加，为了安全考虑取2.0 作为安全系数进行分析。除了弯矩M2z以外，分析其余的力学参数时应按照表4的比值系数。

表4 建议倍数值Table 4 Unequal height difference situation

由表4 可知，M2z的比值系数变化较大。对NRLH58J-1440 和LGJ-500/45 两种导线在同样条件下分析时，建议采用以下步骤完成计算：① 计算LGJ-500/45 型导线在相同的水平间距-竖直高差工况下的和；② 根据前文分析结果，取M1z=；③ 比较M1z和的两者大小，若两者差值较小（比如两者为同一数量级级），则取|M2z| = 2|M1z|；④ 若M1z和的值相差较大，则取|M2z| = |M1z|；⑤ 由于很难判定M2z的正负号，则分别把|M2z|和-|M2z|依次加载于线夹上进行计算，根据两者的分析结果确定最不利荷载值。