下行RⅠS-NOMA的用户集群方法*

彭艺， 吴桐， 杨青青

1.昆明理工大学信息工程与自动化学院，云南 昆明 650500

2.云南省计算机技术应用重点实验室，云南 昆明 650500

可重构智能表面（RⅠS， reconfigurable intelli‐gent surface）是由亚波长单元组成的亚表面，亚表面具有可调的电磁响应，在光与物质相互作用期间由外部信号振幅、相位、偏振和频率等进行控制（Wu et al.， 2020； Liaskos et al.， 2018），形成实时可重构的无线传播环境，从而增强信号的覆盖范围，提高无线通信网络的频谱效率和能源效率，在6G 网络的发展中受到广泛关注（Elmossallamy et al.， 2020； Di Renzo et al.， 2020； Björnson et al.，2020）。

非正交多址接入（NOMA， non-orthogonal mul‐tiple access），通过复用功率的方式，在同一时频资源块上服务多个用户，实现提高通信网络频谱效率和平衡用户公平性的目的（Zeng et al.， 2018）。NOMA 的性能很大程度上依赖于用户的信道条件，而RⅠS具备改善用户信道的能力，二者的结合可实现更灵活的性能权衡与更高的系统增益。文献表明，RⅠS 可有效提升NOMA 系统的速率并降低功耗，且相较于RⅠS 辅助正交多址（OMA， orthogonal multiple access）方案，可以显著降低基站的发射功率（Mu et al.， 2020； Zheng et al.， 2020）。学者进一步研究了RⅠS-NOMA 系统的功率分配（PA， power allocation）与波束形成，以及算法的凸优化和性能问题（田心记等， 2022； 彭艺等， 2023； 季薇等，2023）。

为使RⅠS-NOMA 可应对更复杂的通信环境，还需考虑用户间干扰、蜂窝间干扰、以及系统复杂度等因素。有学者提出采用聚类的方案将用户划分为不同的集群（UC， user clustering），以达到平衡系统增益并降低系统复杂度的目的。RⅠS 的部署方案被分为集中式和分布式，前者让各UC 共享同一被动波束形成（PB， passive beamforming）以获得更大的信道增益，后者为各UC 分别进行PB，既可有效降低系统复杂度，又使RⅠS的部署更具灵活性（Zhang et al.， 2021）。针对集中式RⅠS的UC方案，文献（Gao et al.， 2022）提出利用K-means 为用户聚类，并利用机器学习方法优化波束形成。结果表明，系统的增益与UC 数量息息相关。针对分布式RⅠS 的UC 方案，文献（Yang et al.， 2022）提出一种采用中断概率进行UC 的方法，同时设计了统一的预编码器和解码器以消除UC 间干扰；文献（Elhattab et al.， 2022）提出一种在双蜂窝的下行系统中，中心用户与边缘用户配对的UC 策略，利用RⅠS增强边缘用户的通信质量。

以上研究主要针对用户分布较为均匀或用户数量较少的特定场景。将RⅠS-NOMA 集成到未来的无线网络中，还需要考虑用户分布、用户信道差异以及各UC 用户数量等因素对性能的影响。因此，本文构建了一个视距（LOS， line-of-sight）链路受阻且用户分布非均匀的场景，并提出利用分布式RⅠS 辅助下行NOMA 用户进行通信，引入了多种聚类算法为用户划分集群，以提升系统的频谱效率。此外，为了提升功率增益与信道增益，逐级地为系统进行PA 与PB。本文的研究内容包括：（1）为解决RⅠS-NOMA 的聚类问题，将文献（Kat‐we et al.， 2022）提出的自适应几何分布（AGD，adaptive geometric distribution）聚类算法进行调整，运用到RⅠS-NOMA 模型中，并引入谱聚类（SPC，spectral clustering）、K-means 和高斯混合模型（GMM， Gaussian mixture model）方案进行对比分析。（2）由于涉及的多比率问题难以获得稳定解，且多个目标变量高度耦合，为了使系统可有效地进行PA 和PB，采用文献（Shen et al.， 2018）提出的可解决功率控制和波束形成问题的分式规划（FP，fractional programming）方法，将对数与分数复合的最大化频谱效率问题转换成一系列凸问题，从而允许系统逐级地进行凸优化。研究结果表明，相较于其他UC 方案与OMA 方案，调整过的AGD方案能使用户获得更好的带宽复用增益，同时基于FP 逐级优化PA 与PB 的方法能获得显著功率增益与信道增益。

1 系统模型

1.1 分布式RⅠS辅助NOMA通信模型

如图1 所示，考虑到基站（BS， base station）与用户的LOS 链路被阻挡，在BS 到用户之间部署M块RⅠS 构造非视距（NLOS）链路服务K个用户，并且每个反射面均由N个反射单元组成。假设所有用户位置信息已知，定义二维用户直角坐标为kj=[xj，yj]T，j∈[1，…，K].利用聚类算法将用户划分为L个UC，每块RⅠS 服务一个UC 内的用户(L=M)，各UC 间采用频分多址（FDMA， frequency di‐vision multiple access）进行通信，UC 内用户采用NOMA 进行通信，以保证UC 间信道正交，UC 内信道非正交。

图1 中，Gm∈CN×1和hm.k∈CN×1分别表示BS到第m个RⅠS 和第m个RⅠS 到用户k的信道系数矩阵。其中m∈[1，…，M]，k∈[1，…，K].NOMA采用先获取信道状态信息（CSⅠ，channel state infor‐mation）再传输信号的协议，假设BS、RⅠS 和用户均可获得完美CSⅠ，第l个UC 中第k个用户接收到第m个反射面的信号为

其中上标H表示共轭转置，下标l、m和k分别表示UC、 RⅠS 和 用 户 的 序 号 ，=diag(ejϕm，1，ejϕm，2，…，ejϕm，N)为第m块RⅠS的PB矩阵，Cl和Cl/{k}分别为第l个UC 所有用户的集合和第l个UC 内除去用户k的其他用户集合。Pl，k、sl，k和ul，k分别为第l个UC中第k个用户的功率、信号和零均值高斯加性白噪声ul，k～CN(0，σ2).UC 内用户在功率域上利用连续干扰消除技术（SⅠC，successive interference cancellation）消除部分用户干扰，以解码目标信号。由于存在可以获得完美CSⅠ的前提，可将用户信道增益进行降序排序，作为SⅠC 消除干扰的顺序。为了获得第k个目标信号，需先解码第i个设备的信号(i＜k)，然后按照i= 1，2，3，…，k- 1 的顺序从接收机中消除这些信号，i＞k的信号被视作噪声。第l个UC中第k个用户的SⅠNR为

其中B表示带宽，|Cl|表示第l个UC 的人数。考虑到公平性，为各UC平均分配带宽，第l个UC中第k个用户以bit·s-1·Hz-1为单位的频谱效率为

整个系统中所有用户的频谱效率为

以最大化所有用户的频谱效率为目标，UC 间PA 因子αl、UC 内功率Pl，k、UC 内人数|Cl|和PB矩阵的目标函数为

其中Pmax为最大发射功率，式（5a）-（5b）为BS 发射功率约束；式（5c）-（5d）为UC 间PA 因子约束；式（5e）为保证用户QoS 的最小SⅠNR 约束，并将γmin视作正确执行SⅠC 的最低SⅠNR 要求；式（5f）为PB约束；式（5g）为UC人数约束。

1.2 系统场景设置

如图2 所示，用户在（0，0）为圆心，半径为1 km 的范围内生成。为了符合实际的小区场景，用户分布不完全随机，服从中心到边缘密度逐渐降低的原则。BS位于（1 km，0）处，假设纵轴x= 1处的障碍物阻碍了LOS 链路。考虑到中心用户密度更大，且信道衰落服从由快到慢的原则，将RⅠS部署于中心用户的上方可使RⅠS 距离用户的质心更近，从而有效地提高公平性并改善用户的信道质量。同时，QoS约束保证了系统会利用功率资源补偿数量较少的边缘用户。BS 到各RⅠS 的信道差异对系统的性能影响是无法忽略的，且这种差异主要来自于自由空间损耗。为了让各UC 获得更公平的信道资源，并减小这种差异在系统中产生的不确定性，将RⅠS 部署在（0.1 km，0）、（-0.1 km，0）、（0，0.1 km）和（0，-0.1 km），使BS 到各RⅠS 的欧氏距离相似，从而减小BS到各RⅠS的信道差异。

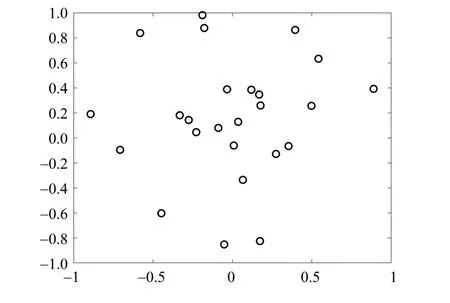
图2 用户分布Fig.2 Users distribution

2 用户聚类方案

2.1 AGD方案

为了应用RⅠS-NOMA 系统模型，将AGD 聚类算法（Katwe et al.， 2022）调整为基于圆心的方法，并设置最大UC数量为L，对用户进行聚类。首先，寻找用户范围的圆心o=[ox，oy]，利用四舍五入的方式固定UC 内最大人数即然后，基于圆心o从0°开始逆时针扫描，将用户按照方位角大小降序排序，找到第 |C1|个用户坐标k1=将这个角度内的用户划分为一个UC即基于上一个UC 的角度扫描下一个UC 的角度，直到完成第L个UC 即φL=最后，将剩下的用户划到最后一个UC内，即各UC的角度φl为

系统主要的信道衰落来自NLOS链路的自由空间损耗。搜索UC 质心与单块RⅠS 质心最小平均距离的方案，作为UC 对RⅠS 的匹配方案。首先根据已知的第l个UC 内用户坐标j∈[1，…，|Cl|]，寻找利用二进制变量zl，m∈{0，1}表示第l个UC 选择与第m块RⅠS 进行通信，定义RⅠS选择矩阵为

RⅠS与用户匹配方案的目标函数表示为

其中rm为第m个RⅠS 的质心坐标，‖ · ‖为欧氏范数。式（8a）为满秩约束，保证每一块RⅠS均在工作；式（8b）为二进制变量约束；式（8c）-（8d）保证各UC均被一块RⅠS所服务。考虑到至多有M！种匹配方案，且二进制规划问题非凸，利用蛮力搜索的方法获得Z的复杂度为O(LM).

AGD 聚类的效果，如图3 所示。在用户分布非均匀的场景下，AGD 具有2 点优势：（1）此方案根据角度与最大人数限制用户聚类，在能获得更均匀聚类效果的同时，保证UC 内用户有较高的余弦相似度；（2）因为用户坐标服从正态分布，此方案中各UC 的用户同样遵循从中心到边缘，密度逐渐降低的分布原则，又因为信道衰落均是由快到慢的，AGD可获得更大的UC内用户信道差异。

图3 AGD聚类效果Fig.3 AGD clustering performance

2.2 SPC方案

SPC 聚类的效果，如图4 所示。SPC 通过拉普拉斯矩阵计算节点之间用户与RⅠS 极坐标的相似度，将这些节点划分为不同的UC，使得每一个UC 中用户数据相似度较高，UC 之间相似度较低。在用户分布非均匀的场景下，边缘用户与中心用户的坐标相似度会对聚类效果产生较大影响，会导致边缘用户被划分至最近UC，使得各UC 用户数量不均匀。

图4 SPC聚类效果Fig.4 SPC clustering performance

2.3 K-means方案

K-means 聚类的效果，如图5 所示。K-means选取4 个RⅠS 坐标作为初始聚类中心，计算每个用户到这4 个UC 中心的距离，将其划分到距离最近的UC 中，重复此过程，直到所有用户都被划分至相应的UC 内。因K-means 将相似欧式距离的用户聚类，在用户分布非均匀的场景下，用户与RⅠS的分布情况均会对聚类效果产生较大影响，会导致各UC内用户信道差异较小且用户数量不均匀。

图5 K-means聚类效果Fig.5 K-means clustering performance

2.4 GMM方案

GMM 聚类的效果，如图6 所示。GMM 假设用户极坐标由若干个高斯分布组成，每个高斯分布对应一个UC，通过贝叶斯公式计算每个数据点属于每个聚类的概率，从而得到最终的UC 结果。GMM 利用概率密度为用户聚类，用户间的距离相似度和每次极大似然估计随机选取的样本数量会对聚类效果产生较大影响。在非均匀用户分布的场景下，会导致UC 内用户余弦相似度较低或距离相似度较高，使得各UC 内用户信道差异较小且用户数量不均匀。

图6 GMM聚类效果Fig.6 GMM clustering performance

2.5 聚类方案实现代价

SPC需要多次计算每个用户与其他用户的坐标相似度，复杂度为O(DLK3I)；K-means 需要计算所有用户与RⅠS 坐标间的欧氏距离，复杂度为O(DLKI)；GMM 需要多次遍历用户坐标以获得多个服从正态分布的UC，复杂度为O(DLKI)；AGD仅需遍历1次用户坐标，复杂度为O(DK+LM)，其中D和I分别代表数据维数和迭代次数。

3 优化算法设计

3.1 分式规划

对于固定的Z，UC 下标l与RⅠS 下标m相同，考虑到公平性原则，利用UC 内人数与总人数之比分配各UC 功率，即αl≤.问题（5）中，优化单个UC内PA与PB的问题表示为

s.t.（5a），（5b），（5e），（5f）.

为求解对数与分数复合的非凸最大化频谱效率问题，采用闭式分式规划进行PA与PB（Shen et al.， 2018）。对式（9）进行拉格朗日对偶变换，有

s.t.（5a），（5b），（5e），（5f）.

s.t.（5a），（5b），（5e），（5f）.

辅助变量δl，k的最优解为

为了分解式（12）耦合的变量Pl，k与Θl，利用固定一个变量优化另一个变量的方式逐级求解Pl，k与Θl，初始化发射功率为|Cl|阶单位矩阵）获得；利用初始化的与优化Pl，k，再利用Pl，k与优化Θl.

3.2 功率分配

s.t.（5a），（5b），（5f）.

利用二次变换将分式问题（13）进一步转换为

s.t.（5a），（5b），（5f）.

易知PA 问题（14）为凸优化问题，将其赋值后利用CⅤX工具求解。

3.3 被动波束形成

令hl，k◦Gl=Hl，k，其中◦表示哈达玛积，对于固定的δl与Pl，式（11）中优化PB的问题表示为

s.t.（5e），（5f）.

对式（16）进行二次变换，得

s.t.（5e），（5f）.

由于问题（17）中QoS 约束5f 非凸，利用二次锥规划的方法（Xie et al.，2021）将其转换为

问题（17）进一步表示为

4 仿真分析

4.1 实验设计

路径损耗参照宏小区的自由空间损耗模型，阴影效应τ服从均值为0，标准差为3 dB 的正态分布。为使系统可有效收敛，以增长率是否小于收敛阈值作为停止迭代的准则。为了验证AGD 的自适应能力，设置的用户数量不能被UC 个数整除。为使仿真与理论一致，信道矩阵取103次实验结果的平均值获得。为使QoS 约束能适用于所有实验方案，设置γmin= -10 dB。具体参数由表1给出。

表1 系统参数Table 1 System parameters

4.2 聚类效果对比

表2 为4 种聚类方案用户数的方差，可以看出AGD 具有更均匀的聚类效果。表3为4种聚类方案下，Θ 为单位矩阵时，各UC 的初始信道增益平均标准差。可以看出，AGD方案下UC内用户信道差异更大，这可解释为AGD 可使用户间角度尽可能地相近，欧氏距离相对较远。这说明AGD 可构造更大的信道差异，减小串行干扰。

表2 人数方差Table 2 Ⅴariance in number of users

表3 信道增益平均标准差Table 3 Average standard deviation in channel gains

4.3 收敛性分析

在处理功率控制和波束形成最大化速率的问题时，需要平衡各个用户的SⅠNR，同时还需要考虑对数函数的增长率。随着最大发射功率和反射单元数量N的增加，解空间也会扩大，即使通过拉格朗日对偶变换将其转化为多比率分式规划问题，优化算法也难以确保全局收敛。 图7 为Pmax= 43 dBm，N= 25 时，单个UC 在不同用户数量方案下的频谱效率收敛效果。第一次迭代的结果为平均分配功率方案下的频谱效率。将收敛阈值设置为0.5 × 10-4，频谱效率均能收敛；并且，随着用户数量的增加，收敛所需的迭代次数逐渐增加。由此可知，SPC、K-means 和GMM 出现不均匀的聚类效果时，会导致某个UC 内用户数量过大，增加了求解难度。PA 与PB方案中的二次变换虽然不能保证算法搜索到全局最优解，但可以收敛至一个稳定点，还能将收敛速度严格控制在超线性收敛速度之下，避免算法过早陷入局部最优解。换言之，较慢收敛速度可能有利于算法充分地探索更大的解空间（Shen et al.，2018）。

图7 不同用户数量的频谱效率Fig.7 Spectrum efficiency with different number of users

4.4 频谱效率对比

为了说明NOMA 的优势以及FP 方法对PB 的有效性，与加入了OMA 与随机控制方案进行PB的方案进行对比。OMA 方案为：在AGD 的基础上，进一步为UC 内每个用户划分频率资源块，保证每个用户信道正交并为每个用户平均分配功率，利用半正定松弛进行PB。Random 方案为：在FP为用户进行PA 的基础上，利用随机相移为用户进行PB。

图8 为N= 25 时4 种聚类方案与OMA 方案在不同发射功率下的频谱效率。随着发射功率提升到40 dBm，相较于SPC、K-means 与GMM 方案，AGD 方案的增益提升了7%、14%、19%和42%。这可解释为：在此聚类方案下，各UC 用户数量更均匀，能获得更好的带宽复用增益；而在SPC、K-means 与GMM 方案下，UC 内用户数量不均匀且信道差异较小，导致复用增益较低，串行干扰较大。OMA 不受带宽复用增益，需要更大的能量成本实现性能提升。

图8 不同发射功率下的频谱效率Fig.8 Spectrum efficiency with different transmit power

图9 为Pmax= 43 dBm 时4 种聚类方案在不同RⅠS 反射单元数量下的频谱效率差异。相较于SPC、K-means 与GMM 方案，AGD 方案的增益提升了16%、19%、26%和40%。这可解释为：在此聚类方案下，各UC 用户数量相对均匀，实现了更好的带宽复用增益，有效地平衡了各UC 的串行干扰。此外，UC 内用户欧氏距离相对较远，余弦相似度较高，系统能获得更大的信道差异，减少了串行干扰，从而进一步提高了系统频谱效率。在SPC、K-means和GMM方案中，各UC用户数量不均匀，受复用增益较小。由增长率可以看出，性能更依赖RⅠS 带来的信道增益；同理，OMA 不受带宽复用增益，需要更大的RⅠS硬件成本实现性能提升。相较于随机控制PB 的方案，基于FP 的PB方案能获得更大的信道增益，这可利用与约束C5等效的欧式范数约束≤N2解释，即在FP 的优化下，信道能获得接近N2的增益。

图9 不同反射单元数量下的频谱效率Fig.9 Spectrum efficiency with different number of RⅠS units

在N= 25 时，将AGD 方案下的第一个UC 内的用户按信道增益降序的方式逐个加入系统。在不用发射功率下，频谱效率与用户数量的关系如图10所示。随着用户数量的增加，3种发射功率方案下的频谱效率（实线）与平均频谱效率（虚线）均呈下降趋势。由此可知，串行干扰会对系统性能产生较大的影响，且这种影响与功率大小无关。相对均匀的UC 用户数量能有效地平衡各UC 的串行干扰，以提升系统性能。

图10 不同用户数量下的频谱效率Fig.10 Spectrum efficiency with different number of users

5 结 语

为提升下行RⅠS-NOMA 系统在非均匀用户分布场景中的性能，提出一种分布式RⅠS 辅助下行NOMA 的用户聚类方案。以最大化用户频谱效率为目标，利用AGD 进行UC，并利用基于FP 的方法逐级优化PA 与PB。仿真结果表明，相较于其他聚类方案，AGD 可获得更均匀的聚类效果和更大的UC 内信道差异，从而提高带宽复用增益并减小串行干扰；同时，FP 有效地提升了功率增益与信道增益。由于本文主要讨论聚类方案对系统性能的影响，结论均是基于完美执行SⅠC这一前提下获得的。因此，在未来的工作中，需要加强RⅠS 与SⅠC的结合，以进一步研究系统性能。