一种宽带高灵敏水声换能器的有限元分析
2024-02-23吴萌萌夏丽莉王宏伟魏彤
吴萌萌,夏丽莉,王宏伟,魏彤
(北京信息科技大学 理学院,北京 100192)
0 引言
声呐系统最前端的设备是水声换能器,它也是声呐系统与水介质相互作用、交流信息的通道[1]。随着微型目标探测与水下定位等应用对空间分辨能力要求的提高,高频(>100 kHz)宽带水声换能器越来越受到重视[2-4]。
目前,提高水声换能器的带宽主要是通过改变压电材料本身的特性和利用多模耦合理论来实现的[5-6]。改变压电材料的特性主要是通过添加柔性聚合物来增加损耗,降低换能器敏感元件的机械品质因数以及增加换能器的带宽[7]。多模耦合理论的应用,第一种是将不同结构的敏感元件进行组合[8],使其产生的不同频带范围的振动模态达到耦合的效果,从而实现换能器带宽的拓展;第二种是添加匹配层[9],但随着时间的推移,匹配层的性能会退化[10],造成换能器性能的不稳定。
换能器的灵敏度主要与压电材料的机电耦合系数有关[11-12]。提高压电材料的机电耦合系数的方法主要是在结构上改进,以实现将敏感元件的厚度振动转换为长度伸缩振动[13]。典型地,1-3型和1-3-2型压电复合材料就是将敏感元件的厚度振动转换为压电柱的纵向振动,从而提高了机电耦合系数。但是压电柱间聚合物的影响,会在一定程度上增加损耗[14-15],降低有效机电耦合系数。
为了达到换能器宽带高灵敏这一目的,本文采用双金属板压电陶瓷柱阵列材料作为换能器敏感元件。一方面,在压电柱之间采用以空气代替聚合物的方式,将压电材料的厚度振动转化为较为纯净的压电柱的纵向长度伸缩振动,提高压电材料的有效机电耦合系数;另一方面,上表面覆盖的金属板除了起到电极的作用外,还能通过对敏感元件进行应力放大,使其灵敏度提高[16]。在结构上,将4块不同厚度的双金属板压电陶瓷柱阵列材料敏感元件嵌套式粘接,利用多模耦合理论使产生的不同的频段进行叠加,以实现带宽的拓展。
1 敏感元件结构
双金属板压电陶瓷柱阵列材料是由压电陶瓷柱阵列和金属板组成。制作过程是将整个压电陶瓷分别沿x轴和y轴方向切割,得到具有一半衬底的一系列周期性排列的压电陶瓷柱,并在压电陶瓷柱阵列上表面粘接覆盖薄金属板;再以同样的方法反向切割,并粘接覆盖厚金属板。其结构如图1所示。这种结构使用空气代替压电复合材料中的聚合物,使压电柱之间的横向耦合得以减弱。同时,该结构的压电材料将厚度振动模态转化为周期性排列的压电柱的长度伸缩振动。此外,由于金属盖板的覆盖提高了压电陶瓷柱的受压,增加了压电柱的纵向电压,从而增加了输出电压,提高了灵敏度。
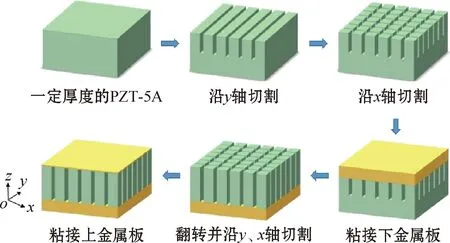
图1 双金属板压电陶瓷柱阵列制作工艺Fig.1 Bimetallic plate piezoelectric ceramic column array fabrication process
换能器敏感元件的整体结构如图2所示。为了实现平整的辐射面,需要将4块不同厚度的敏感元件粘接在不同厚度的硬质泡沫上。通过合理设计不同厚度的双金属板压电陶瓷柱阵列敏感元件,使其实现频带叠加,进而扩大换能器的工作带宽。

图2 敏感元件结构Fig.2 Sensitive element structure
2 理论分析
双金属板压电陶瓷柱阵列材料结构包括压电陶瓷柱阵列、上下金属板。其中压电陶瓷阵列柱表现为长度伸缩振动模态[17],因此应力分量T1=T2=T4=T5=T6=0、T3≠0,电场强度分量E1=E2=0、E3≠0。可以得到简化后的g型压电方程:
(1)

将式(1)变换可以得到:
(2)
式(2)在z方向进行积分可得压电陶瓷两端电压:
(3)
式中:l为压电陶瓷柱长度;ζ1、ζ2分别为z=0和z=l处的位移。
由式(2)可得压电陶瓷柱的电路状态方程:
I=jωsD3=jωC0V-n(v1+v2)
(4)

压电陶瓷柱的运动方程为
(5)

对式(5)求解可得:
(6)

机械振动方程为
(7)
式中:F1、F2为z=0和z=l处的外力。根据式(4)和式(7)推出压电陶瓷柱的机电等效图如图3所示。
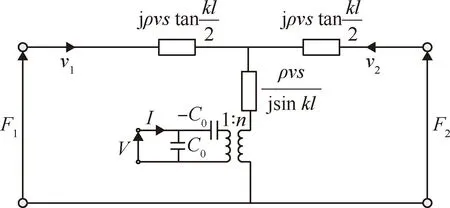
图3 压电陶瓷柱的机电等效图Fig.3 Electromechanical equivalent diagram of a piezoelectric ceramic column
对于下金属板来说,其振动模态表现为厚度振动。因金属板不具备压电效应,故对于金属板来说,其压电常数分量为 0。由于下金属板与压电陶瓷柱完全粘接,可认为接触面振速相同,则下金属板所对应的机械运动方程为
(8)

下金属板的机电等效图如图4所示。

图4 下金属板的机电等效图Fig.4 Electromechanical equivalent diagram of the lower metal plate
上金属盖板振动也为厚度振动模态。类似地,将压电常数分量设置为零,即可得到上金属盖板的机电等效图,如图5所示。

图5 上金属盖板的机电等效图Fig.5 Electromechanical equivalent diagram of the upper metal cover plate

因上下金属板与压电陶瓷柱的接触面之间具有相同的边界条件,因此双金属板压电陶瓷柱阵列材料整体机电等效图是将各部分机电等效图连接起来得到的,如图6所示。

图6 双金属板压电陶瓷材料的机电等效电路Fig.6 Electromechanical equivalent circuit of bimetallic plate piezoelectric ceramic material

简化后的双金属板压电陶瓷材料等效网络电流图如图7所示。

图7 双金属板压电陶瓷材料的等效网络电流图Fig.7 Equivalent network current diagram of bimetallic plate piezoelectric ceramic material
图7中,zq1=zm1+za1+zm1zf1/(zm1+zf1),zq2=za1+zm2+zm2zf2/(zm2+zf2),zq3=zb1+jn2/(ωc0)。求得回路电流方程为
(9)
式中:Vq1为施加在金属板表面的电压。
将双金属板压电陶瓷材料的压电陶瓷及金属板参数带入电流方程,即可求得最大电流,此时辐射面最大振速对应的频率即为换能器串联谐振频率。由动量守恒定律可知,为了使辐射面具有更好的性能,要求上金属盖板辐射面所需要的振速和振动位移均比下金属板要大,因此上金属盖板质量应比下金属板轻。在选择下金属板的材料时,考虑其硬度、刚度以及质量等问题,选择了铜和钢2种材质。考虑实际制作工艺的要求,下金属板的厚度选择2.0 mm,上金属盖板均为厚度为0.2 mm的铜板。代入相关参数进行计算,可得到双金属板压电陶瓷材料的串联谐振频率随压电陶瓷柱高度变化曲线如图8所示。从图8可知,无论选择哪种材料作为下金属板,双金属板压电陶瓷材料的谐振频率均随压电陶瓷柱的高度增加而降低;在压电陶瓷柱高度相同的情况下,下表面为钢板时的谐振频率比下表面为铜板时的要高。这为后续双金属板的材质选择提供了参考。

图8 谐振频率随压电柱高度的变化曲线Fig.8 Variation curve of resonant frequency with height of piezoelectric post
3 有限元仿真分析
利用ANSYS有限元软件[18]对双金属板压电陶瓷柱阵列谐振频率与上金属盖板厚度的关系进行了研究,根据仿真结果确定上金属盖板的最佳厚度;接着,在最佳的上金属盖板厚度下,仿真分析了谐振频率与压电陶瓷柱高度的关系,并比较下金属板为铜和钢两种情况时的机电参数。最后,通过建立有限元模型,对敏感元件整体进行仿真分析,为敏感元件以及换能器的设计提供理论支撑。
3.1 谐振频率与上金属盖板厚度的关系
在敏感元件振动时,下金属板主要起到质量块以及对敏感元件稳定的作用;上金属盖板粘附在辐射面随压电陶瓷柱一起振动,起到了应力放大的作用。因此,仅考虑上金属盖板的厚度对双金属板压电陶瓷柱阵列敏感元件振动的影响。通过有限元软件建立不同厚度上金属盖板的压电陶瓷柱模型,仿真分析其谐振频率以及有效机电耦合系数的变化规律。双金属板压电陶瓷柱的有限元模型如图9所示。其中压电陶瓷柱的长宽均为1.5 mm,高度为5.0 mm。由振动模态图可知,上金属盖板辐射面处的振动最为强烈,说明该阵列上覆的金属板具有应力放大效应,符合设计预期。

图9 双金属板压电材料周期单元有限元模型Fig.9 Finite element model of periodic unit of bimetallic plate piezoelectric material
不同厚度的上金属盖板的双金属板压电陶瓷柱的导纳曲线如图10所示。压电材料的谐振频率为导纳曲线的最高点,反谐振频率为导纳曲线的最低点。压电材料机电性能变化曲线如图11所示。仿真结果表明,随着上金属盖板厚度的增加,谐振频率与反谐振频率均逐渐降低,其有效机电耦合系数在0.6~0.7之间波动。考虑到传声效果,上金属盖板应尽量薄而硬。根据工艺制作要求,实际制作换能器时,应选用厚度为0.2 mm的铜板作为上金属盖板。

图10 不同厚度的上金属盖板的导纳曲线Fig.10 Admittance curves of the upper metal plate with different thickness

图11 机电参数随上金属盖板厚度变化曲线Fig.11 Variation curve of electromechanical parameters with thickness of upper metal cover plate
3.2 谐振频率与压电柱高度的关系
分别选择厚度为2.0 mm的铜板和钢板作为下金属板,上金属盖板均为厚度为0.2 mm的铜板,建立有限元模型,压电陶瓷柱的长宽均为1.5 mm,对不同高度的双金属板压电陶瓷柱进行仿真分析,其中柱高度为2.5 mm、3.0 mm、3.5 mm、4.0 mm、4.5 mm、5.0 mm时的导纳曲线如图12所示。从导纳曲线图中读取压电材料的谐振频率和反谐振频率,经计算即可得到压电材料的有效机电耦合系数。下金属板分别为铜和钢时的机电性能参数对比如图13所示。
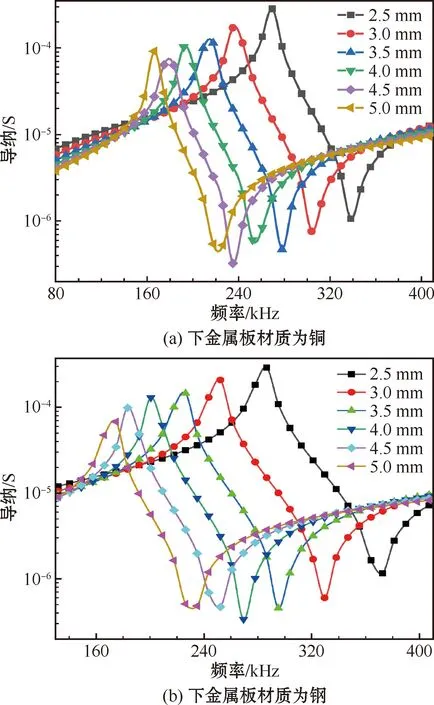
图12 不同高度的压电陶瓷柱对应的导纳曲线Fig.12 Admittance curves corresponding to different heights of piezoelectric ceramic pillars
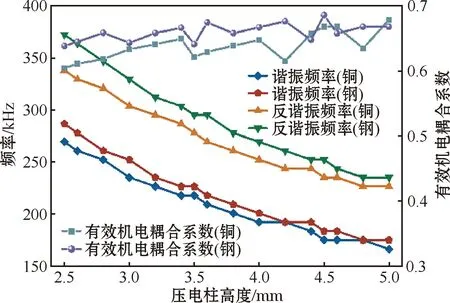
图13 压电材料机电性能参数对比Fig.13 Comparison of electromechanical performance parameters of piezoelectric materials
从图12可以看出,无论是铜还是钢作为下金属板,随压电陶瓷柱高度增加,压电材料的谐振与反谐振频率均降低,这与理论计算结果相符合。由图13可知,2种金属分别作为下金属板时,随压电柱高度的变化,压电材料的有效机电耦合系数均保持在0.6~0.7。金属钢作为下金属板时,双金属板压电陶瓷阵列材料的谐振频率与反谐振频率均比金属铜作为下金属板时高,且压电材料的有效机电耦合系数得到了提高。因此,在实际制作时应选择钢作为下金属板材质。考虑到不同厚度压电材料的耦合效应和工艺制备难度,以及压电陶瓷本身厚度的影响,最终选择了4层压电陶瓷柱的高度分别为4.5 mm、4.0 mm、3.5 mm和3.0 mm。
3.3 敏感元件整体仿真
根据对双金属板压电陶瓷柱阵列材料的一个周期单元的仿真分析最终确定的嵌套式敏感元件厚度分别为4.5 mm、4.0 mm、3.5 mm和3.0 mm,按照嵌套式进行粘接制成换能器的敏感元件,其有限元模型如图14所示。由图14可知,敏感元件整体呈现金字塔型,上金属盖板是厚度为0.2 mm的铜板,下金属板是厚度为2.0 mm的钢板。

图14 敏感元件有限元模型Fig.14 Finite element model of sensitive element
对敏感元件进行仿真分析得到不同厚度敏感元件和整体敏感元件的导纳曲线如图15所示。从图15可看出,该结构的换能器敏感元件的导纳曲线共产生4个峰值,峰值所对应的频率分别为f1=183 kHz、f2=200 kHz、f3=226 kHz、f4=252 kHz,且敏感单元产生的4个谐振峰与4块不同厚度的敏感元件产生的谐振频率相对应。仿真结果表明,该敏感元件的参数设计合理,该结构可以实现多模耦合振动,能够有效实现换能器的频带拓展。

图15 不同厚度和整体敏感元件仿真导纳曲线Fig.15 Admittance curves of the sensitive element with different thickness and overall under simulation
4 换能器水下性能仿真测试
为了更好地验证该结构敏感元件的性能,利用有限元软件,通过建立敏感元件水场模型进行水中性能分析。在水中的导纳曲线如图16所示。图16结果显示,由于水中的阻尼系数较大,4块不同厚度的双金属板压电陶瓷柱阵列材料敏感元件的4个谐振峰在水中耦合为较宽频带范围的谐振峰,换能器工作频率范围为210~290 kHz,工作带宽达到约80 kHz。实测结果与理论仿真结果较为贴合,其产生误差的原因可能是所使用的PZT-5A压电陶瓷的性能参数与有限元模拟中使用的材料参数不同;另外,有限元仿真分析时的网格划分以及水场参数的选择均会产生一定的误差。
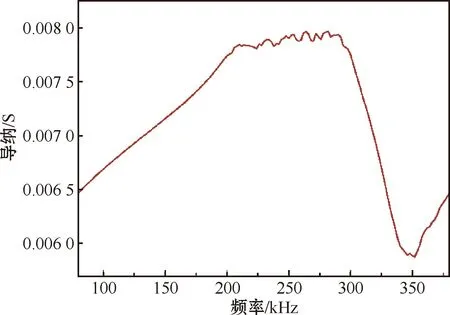
图16 水中的导纳曲线Fig.16 Admittance curve in water
换能器在水中的发送电压响应和接收灵敏度如图17和图18所示。仿真结果表明,该结构敏感元件制作的换能器的最大发送电压响应为188.6 dB,-3 dB带宽约为74 kHz;最大接收灵敏度为-173.9 dB。与大多数水声换能器[19]相比,该结构换能器灵敏度得到一定程度的提高。

图17 发送电压响应曲线Fig.17 Transmit voltage response curve
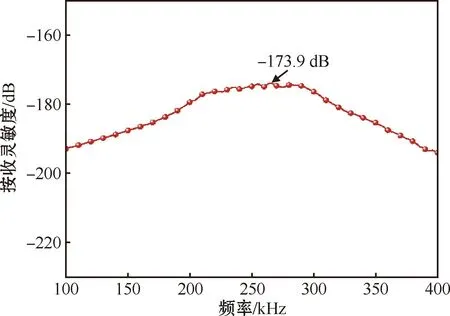
图18 接收灵敏度曲线Fig.18 Receiving sensitivity curve
仿真结果表明,由双金属板压电陶瓷柱阵列材料敏感元件制成的水声换能器,比目前大多数同体积的压电复合材料换能器具有更宽的带宽;另一方面,与目前大多数水声换能器的接收灵敏度(小于-200 dB)相比,该结构敏感元件制成的换能器能够有效提高接收灵敏度。
5 结束语
本文提出了一种嵌套式双金属板压电陶瓷柱阵列压电材料。通过理论推导和有限元仿真分析证明,该结构压电材料具有良好的压电性能,能有效提高换能器的灵敏度,有效拓展换能器带宽。水中仿真测试结果表明,由该结构敏感元件组成的换能器工作频率范围约为210~290 kHz,最大发送电压响应为188.6 dB,-3 dB带宽约为74 kHz,最大接收灵敏度为-173.9 dB。该结构换能器在水下能够实现良好的模态耦合,工作带宽得到有效拓展,且具有较高的灵敏度,因此可应用于水声定位与通信的声呐系统以及水下勘测等。
另外,通过理论与仿真分析讨论了下金属板为不同材料时的压电材料性能,对于双金属板压电材料,下金属板应选择硬度大的材料,且其质量应该尽可能大;上金属盖板应选择硬而轻的材料。这为后续高灵敏换能器的制作提供了理论参考。
