大型飞机多支柱交联式起落架一体化载荷校准及建模研究
2024-02-23汤阿妮郭正旺胡小敏张海涛
汤阿妮, 郭正旺, 胡小敏, 张海涛
(中国飞行试验研究院飞机所,西安,710089)
起落架载荷试飞是验证起落架及其相连结构强度的重要途径,主要采用应变法[1-3]。载荷校准试验是应变法测载的关键环节,起落架载荷校准有联机和脱机两种方法。20世纪末,中国试飞院利用联机方法对多型小型飞机起落架进行了载荷实测[4]。随着舰载机、大型飞机的研制,起落架的限制载荷大幅提升、结构及载荷工况更加复杂[5-7],联机校准已不能满足起落架载荷试飞需求。为满足大载荷复杂工况起落架载荷实测需求,试飞院开展了脱机校准研究,利用该方法陆续完成了多型飞机起落架载荷实测[8]。北京强度研究所也对脱机校准进行了研究,完成了多型飞机起落架载荷谱实测[9-10]。常规布局起落架载荷校准试验技术已相对成熟。
我国自主研制的某大型飞机,首次采用多支柱交联式主起落架。因其下部空间狭小、多支柱交联紧凑设计、载荷量级巨大,载荷校准无论采用联机还是脱机方法难度均很大。如何通过载荷校准获得准确可靠的载荷模型,成为制约飞机试飞定型的重大难题之一。国外多种飞机采用此类起落架结构,如A400M、AN225、AN124等,但该类起落架载荷目前看到的资料以仿真计算居多[11-12]。据了解AN225、AN124均实测了起落架载荷,但未看到具体报告。国内尚未有该类起落架载荷实测资料,文献[13]描述了伊尔76飞机起落架载荷实测结果,该机主起落架虽然是多支柱布局,但主起落架2个支柱之间互相独立,在校准试验时可以当作单支柱处理。
为了解决该机起落架载荷实测技术难题,首先对起落架结构和传力路线进行分析,确定合理的校准方法,设计载荷校准用应变电桥,通过电桥敏感性分析,确定支柱载荷影响方式,建立了基于广义响应系数的支柱消扰建模方法,并利用实测数据进行了验证。该方法对于多支柱起落架载荷实测、结构设计和安全评定具有重要意义。
1 结构形式及传力分析
1.1 结构形式与特点
某大型飞机主起落架为三支柱六轮摇臂式,主要承力结构包括斜支柱、缓冲器、下摇臂、侧撑杆、前撑杆、拱形支架,三支柱通过拱形支架前后串接,大倾角安装,支柱为“工”字截面,如图1所示。
与常规小飞机相比,该起落架结构特点主要有:
1)多支柱交联,载荷存在多条传力路线,支柱载荷之间互相影响,载荷工况复杂;
2)大倾角安装,垂、航载荷耦合严重;
3)支柱采用工字截面,传力路线及受载单一性均较圆形截面更加复杂;
4)三支柱紧凑设计,内部空间有限。
1.2 结构承载与传力分析
起落架承受的载荷分量包括航向载荷Px,作用于轮心,向前为正;垂向载荷Pz,作用于轮心,向上为正;侧向载荷Fy,作用于轮胎接地点,对主起落架指向内侧为正;主起落架航向刹车载荷Fx,作用于轮胎接地点。由于该机起落架为双轮,校准试验中所有载荷需通过2个机轮分别施加,如图1轮轴处所示(由于空间所限,载荷分量仅标注后支柱,前、中支柱只需将下标中的A替换成F、M即可)。起落架载荷传递途径分析如下:
1)航向载荷Px、Fx和垂向载荷Pz通过下摇臂传递给拱形支架、斜支柱及缓冲器,最后传递至机身平衡。由于后支柱通过前支柱拱形支架与机身相连,所以航、垂载荷通过拱形支架上的交联节点向前方支柱传递,从而影响前方支柱受载;
2)侧向载荷Fy沿下摇臂通过侧撑杆传递至机身。因此,每个支柱承受的侧向载荷单独传递,不影响其他支柱受载。
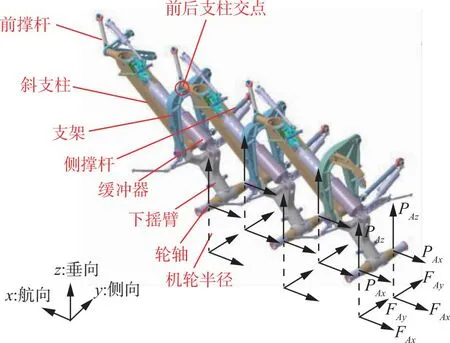
图1 三支柱交联式主起落架及其载荷分量
2 载荷试验
2.1 校准方法
对该机起落架,由于采用大倾角设计,飞机下部空间极为有限,如果采用联机校准,多个载荷工况难以施加,且飞机的固定、试验风险难以估计。综合考虑只能采用脱机方法。以往的脱机校准只有一个支柱,如果该机也采用这种方法,则支柱之间的互相影响将无法考虑,尤其是前、中支柱及中、后支柱之间影响较大,导致较大的测量误差。基于上述分析,对该机宜采用整体脱机校准,即将3个支柱作为一个整体,试验夹具一体设计,三支柱一体安装、一体加载。此外,脱机校准的关键是起落架的固定,不仅要方便安装、拆卸,更重要的是模拟真实状态。以往单支柱起落架,均采用倒装的方式,其优点是缓冲器行程易于固定。对该机起落架,由于起落架固定点与支柱不在同一平面,倒装方式很难实施,试验夹具及加载装置难以固定。综上,对该机起落架采取正装一体化脱机校准,三支柱起落架侧挂正向一体安装,一体加载[14]。
2.2 应变电桥布置
通过受力及传力分析可知,斜支柱和拱形支架主要承受传递航向和垂向载荷,侧撑杆主要承受传递侧向载荷,前撑杆承受传递航向载荷,下摇臂承受三向载荷。据此,分别在下摇臂、支柱、支架、侧撑杆及前撑杆上布置相应载荷电桥,每个支柱布置25个电桥,如图2(a)所示。
对斜支柱及工字截面组桥方式进行了专门设计,直支柱或小倾角支柱测试剖面一般取与轴线垂直的截面,对称组桥。考虑到该支柱的大倾角,除了布置与支柱轴线垂直的测试截面外,还布置了与载荷垂直的电桥;针对工字截面则选取了受载严重的外缘对称面进行组桥。部分测试剖面及电桥布置细节如图2(b)、(c)所示。
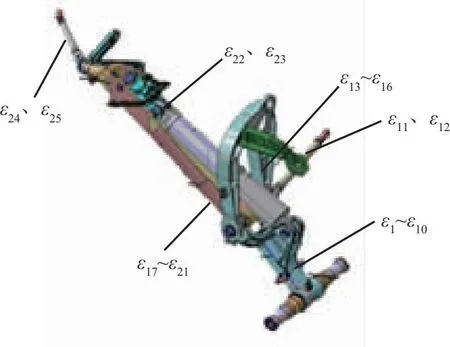
(a)单个支柱应变布置示意图
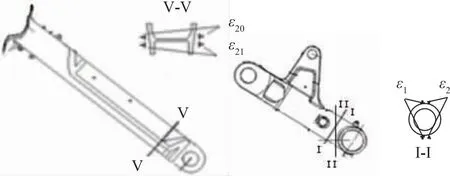
(b)斜支柱 (c)下摇臂
2.3 载荷工况
一体校准与单支柱分别校准最大的区别是,载荷工况不仅要考虑支柱单独受载,还要考虑支柱组合受载。由传力分析可知,后支柱载荷向中支柱传递,中支柱载荷向前支柱传递,前后支柱无影响,侧向载荷独立传递。故支柱组合加载不必考虑前、后支柱组合及侧向组合。
依据载荷分析,载荷工况包含3种缓冲器压缩行程下的单支柱单向加载(含航、垂、侧及刹车载荷)、组合加载(含两向组合及三向组合);两支柱组合加载(含前、中组合及后、中组合)及三支柱组合加载等。两支柱组合进行垂、航、垂航及垂侧组合加载,三支柱进行垂、航、垂航、垂侧、垂航侧组合加载。最大校准载荷为限制载荷的50%,如表1所示。

表1 校准载荷工况
3 载荷建模及验证
3.1 载荷建模
3.1.1 建模基本原理
载荷校准的理论基础是力的线弹性理论和应变的线性叠加原理,即在弹性范围内,应变和载荷成线性关系,且结构应变是所有载荷引起的应变之和。载荷模型如式(1)所示:
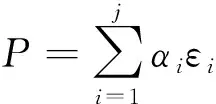
(1)
式中:P为外载荷;ε为结构应变;α为载荷系数;j为电桥个数。对该起落架,载荷模型展开的表达式为:
PFx=α11ε1+α12ε2+…+α1jεjPFz=α21ε1+α22ε2+…+α2jεjFFy=α31ε1+α32ε2+…+α3jεjPMx=α41ε1+α42ε2+…+α4jεjPMz=α51ε1+α52ε2+…+α5jεjFMy=α61ε1+α62ε2+…+α6jεjPAx=α71ε1+α72ε2+…+α7jεjPAz=α81ε1+α82ε2+…+α8jεjFAy=α91ε1+α92ε2+…+α9jεj
(2)
载荷建模的基本任务是求出各个载荷分量的载荷系数,利用校准试验数据,可用最小二乘法计算。近几年也有采用神经网络进行载荷建模的[15],但其内部原理是类似的。以其中一向载荷为例,假设试验样本数为n,则载荷计算模型可用矩阵表示为:
[Pn]=[εnj][αj]
(3)
两边各乘以电桥响应的转置矩阵,得到回归分析的最小二乘法正则方程为:
[εnj]T[Pn]=[εnj]T[εnj][αj]
(4)
由此得到载荷系数为
[αj]=[[εnj]T[εnj]]-1[εnj]T[Pn]
(5)
上式有解的必要条件是|[εnj]T[εnj]|>0
该必要条件的物理意义是:相同特性的电桥不能出现在同一载荷模型中,即所选电桥应当线性无关。对于单支柱起落架,通过响应系数分析,确定每向载荷的最优电桥,即可用上述方法计算得到载荷模型。对多支柱起落架,各支柱电桥除受自身载荷影响外,还受到其它支柱载荷影响,因此不能直接利用上述方法计算,必须解决支柱之间的载荷是如何相互影响的问题。
3.1.2 电桥敏感性分析
电桥敏感性通过响应系数进行分析,响应系数指单位载荷引起的应变[16-17],其表达式为:
β=ε/P
(6)
对于常规布局起落架,载荷分量共3个(刹车载荷为刹车状态的航向载荷),故每个电桥有3个响应系数,即航向载荷响应系数β_Px、垂向载荷响应系数β_Pz和侧向载荷响应系数β_Fy。对多支柱起落架,为分析其它支柱载荷影响,引入广义支柱载荷响应系数的概念(后简称响应系数),即其它支柱载荷引起的电桥响应。所以每个电桥除自身的3个响应系数外,还有另外2个支柱3向载荷的响应系数,共9个响应系数。
响应系数分析包括量值和曲线分析,其量值大小直接反应了电桥的敏感程度,随缓冲器行程变化的曲线则反应了其载荷特性。图3给出的是左主起前支柱2个电桥的响应系数曲线,其横坐标为缓冲器压缩行程。从曲线可以看出,第1个电桥仅对前支柱载荷敏感,且对垂向载荷最敏感,是典型的弯矩电桥特性。第2个电桥除对前支柱三向载荷均敏感外,同时对中支柱航、垂载荷敏感,对后支柱载荷及中支柱侧向载荷不敏感,同时表现出剪力和弯矩电桥特性。

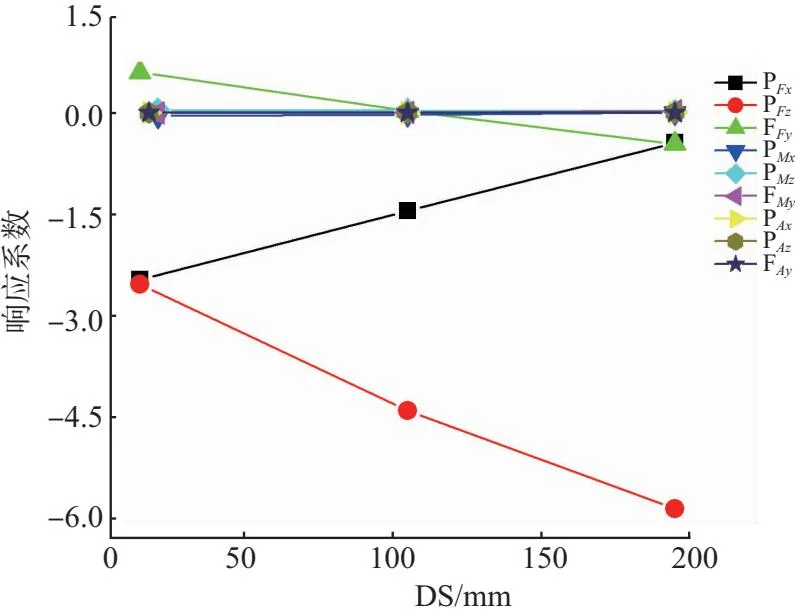
图3 典型电桥响应系数曲线
3.1.3 支柱影响分析
通过广义响应系数量值可以确定多支柱之间载荷的相互影响问题,图4分别给出了一个行程下三支柱不同方向加载时,左主起落架所有电桥的响应系数量值,横坐标为电桥编号,1~25号为前支柱电桥,26~50号为中支柱电桥,其余为后支柱电桥。从图中可以直观地看到一个支柱加载时其它支柱电桥的响应。
由图4可知,后支柱航、垂载荷影响部分中支柱电桥,中支柱航、垂载荷影响部分前支柱电桥。前支柱载荷对中、后支柱所有电桥几乎无影响。后支柱电桥不受前、中支柱载荷影响。所有支柱侧向载荷对其它支柱均无影响。即载荷向前单向传递,与载荷传递分析结果完全一致。

(a)前支柱加载

(b)中支柱加载
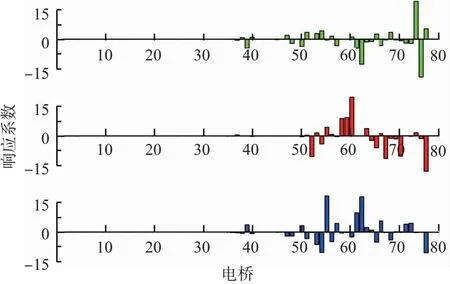
(c)后支柱加载
3.1.4 基于广义响应系数的支柱消扰建模方法
按照式(2),可以把三支柱起落架看作一个九分量受载整体进行一体化建模,每个载荷分量的模型包含所有支柱可能的电桥。通过广义响应系数分析知,支柱载荷向前单向传递,后影响中,中不影响后,中影响前,前不影响后。若采用一体化建模,易产生奇异矩阵,致使无法求解。若完全采用与小飞机类似的单个支柱独立建模,则支柱之间的影响无法消除,载荷模型将有较大误差。为了消除支柱向前单向影响问题,提出支柱独立建模、载荷逐次迭代计算、基于响应系数的支柱消扰建模方法。其基本原则是:每个支柱独立建模,根据广义响应系数,计算出后支柱载荷引起的前支柱应变,将其从总应变中扣除,载荷模型表达式变为:
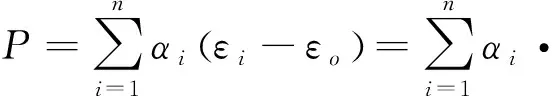
(7)
式中:εo表示其它支柱载荷产生的应变;Pj为其它支柱载荷;βj为对应的广义响应系数。
计算步骤为:
1)优先选择不受其它支柱影响的电桥,对所有载荷单独建模;
2)计算不受其它支柱影响的后支柱载荷;
3)根据响应系数计算后支柱载荷引起的中支柱应变;
4)扣除后支柱载荷引起的中支柱应变,计算中支柱载荷;
5)根据响应系数计算中支柱载荷引起的前支柱应变;
6)扣除中支柱载荷引起的前支柱应变,计算前支柱载荷。
3.2 模型验证
3.2.1 试验验证
以中支柱垂、航载荷为例,通过响应系数分析,选择了8个电桥建立垂向载荷模型,7个电桥建立航向载荷模型,载荷模型分别为:
PMx=-0.048 3ε1+0.007 9ε2+0.01ε3-0.013 7ε4-0.089ε5-0.046ε6-0.003ε7
(8)
PMz=-0.021ε1-0.137ε2-0.145ε3-0.087ε4+0.056ε5-0.256ε6+0.024ε7+0.012ε8
(9)
建模用的电桥对后支柱载荷的响应系数β_PAx、β_PAz、β_FAy如表2所示。可以看出垂向模型中6号和8号电桥受后支柱航向和垂向载荷的响应较大,4号、5号电桥略有影响;航向模型中5号和7号电桥响应较大。对侧向载荷响应均较小。利用未参与建模的载荷工况对模型进行检验,结果如图5所示。所有载荷通过除以最大垂向载荷进行了无量纲化处理。其中PMx0、PMz0是实际加载数据,PMx1、PMz1是未扣除后支柱载荷影响依据模型计算的载荷,最大误差达到5.86%,不满足载荷校准建模误差不大于5%的要求[18]。PMx2、PMz2是利用新模型扣除后支柱影响后的检验效果,最大误差2.5%,满足误差不大于5%的要求。
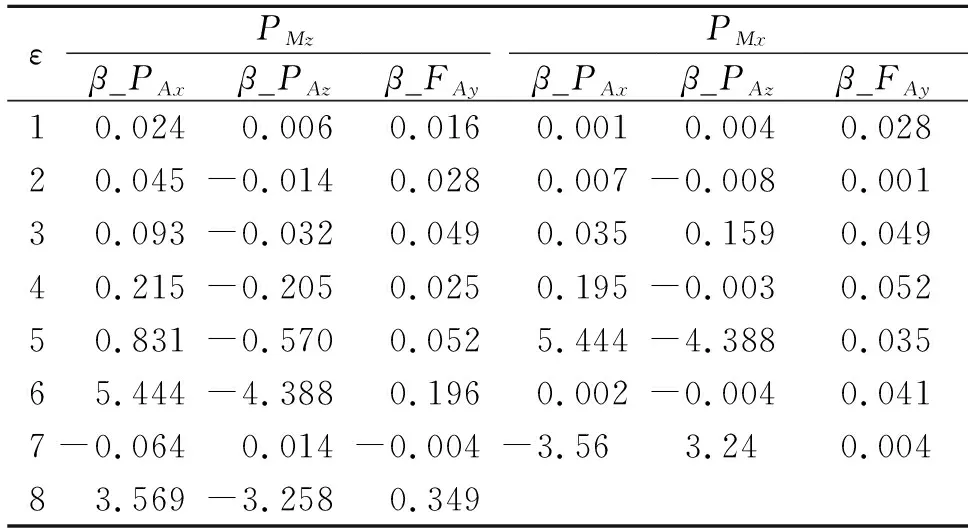
表2 中支柱载荷模型电桥对后支柱载荷的响应系数
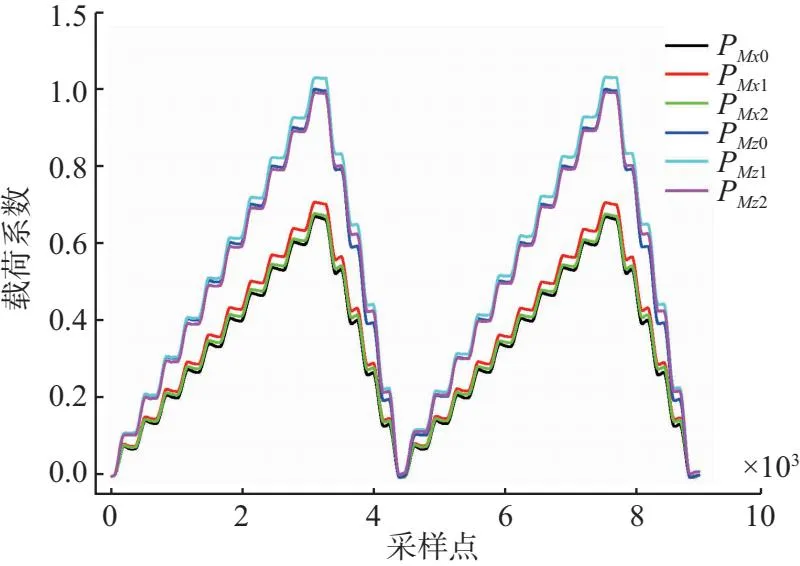
图5 载荷模型验证结果
3.2.2 飞行实测验证
图6给出了某次着陆过程左主起落架实测三向载荷及缓冲器压缩行程(DS)时间历程曲线。DSF、DSM、DSA分别为前、中、后缓冲器压缩行程,其中载荷通过除以停机载荷(PT)、缓冲器压缩行程通过除以最大压缩量(DSmax)进行了无量纲化处理。下沉速度2.8 m/s,着陆俯仰角3.8°。由图6可见后支柱、中支柱、前支柱顺次着陆接地,垂向载荷逐次减小,起转、回弹载荷比较接近,侧向载荷较小,与飞机以3.8°俯仰角着陆状态相符。垂向载荷与缓冲器压缩行程变化趋势一致、量值相符,起转、回弹载荷与垂向载荷量值及相位符合着陆过程。说明载荷变化规律及量值正确,载荷实测结果是可靠的。
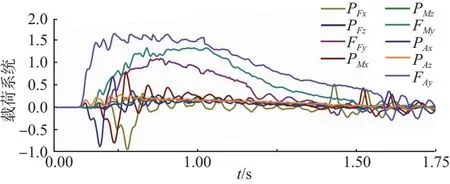
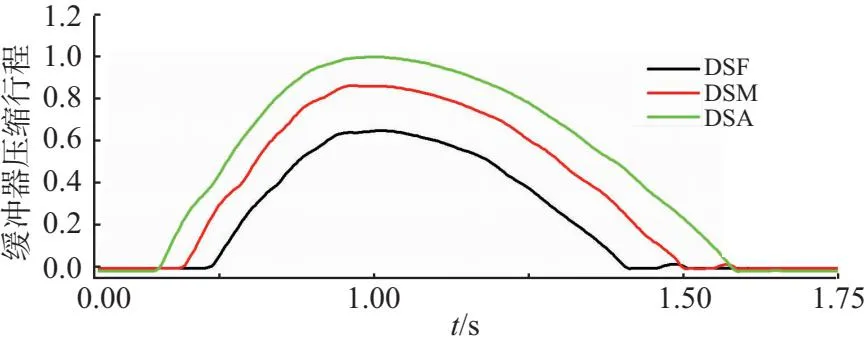
图6 典型着陆起落架实测载荷时间历程
4 结论
针对大型飞机多支柱交联式起落架载荷校准难题,开展了多支柱交联式起落架结构和传力分析,依据其特点,确定校准方法、设计电桥布置方案及载荷工况,基于电桥敏感性分析,提出了基于广义响应系数的支柱消扰建模技术,并通过飞行实测进行验证,得到如下结论:
1)采取的一体校准、独立建模试验方法,符合多支柱交联式起落架结构受力及传力特点,解决了交联式多支柱起落架支柱载荷影响问题,可推广用于类似结构载荷校准及建模;
2)基于广义响应系数的支柱消扰建模方法,解决了交联式多支柱载荷向前单向传递的问题,获得了满足精度要求的载荷模型;
3)地面试验和飞行实测验证了本文一体校准、独立建模思想的正确性,可用于其它大型飞机同类起落架结构载荷实测验证。
