基于浅地层剖面数据和改进地声模型的底质反演方法

2024-02-22孙振银王虎李冠霖

海洋地质与第四纪地质 2024年1期

孙振银，王虎,2，李冠霖

1. 天津大学海洋科学与技术学院，天津 300072

2. 自然资源部海洋观测技术重点实验室，天津 300112

海底底质探测主要用于获取海底浅表沉积物的类型和性质，是海洋地质调查、海洋工程勘察与海洋测绘的重要内容[1]。海底底质探测主要有底质取样分析和声学遥测两种技术手段。底质取样分析，即利用蚌式、箱式、重力等取样器现场采取底质样品并在船上或实验室开展分析测试，是获取底质分类和性质最直接、最有效的方法，但耗资大、耗时长、只能获取离散点的底质信息。基于声学遥测进行海底底质探测，指利用单波束、多波束、侧扫声呐等声学遥测手段获得海底反向散射强度或声呐图像[2]并从中提取谱特征、纹理特征[3]、角度响应曲线[4]、分形维[5]、反向散射强度[6-8]等进行底质识别，其测量效率高，可获取线、面形式的相对连续的底质信息，已形成了相应的商业软件[9]。然而，海底反向散射强度和声呐图像主要通过高频声学信号获取，包含了底质类型与性质，以及海底地形、微地貌、底栖生物等在内的海底面综合信息，精确解译底质信息难度大。

浅地层剖面仪是另一种常见的声学遥测设备，与单波束、多波束、侧扫声呐相比，其工作频率更低[10]，近似正向入射的声波可穿透海底面进入沉积层内部[11]，接收海底面及各沉积层面的反射波。目前，浅地层剖面探测主要用于获取水下浅部地层结构与构造[12]，已有学者尝试从浅地层剖面数据中提取声衰减、声阻抗、海底反射损失等参数[13-17]，基于这些参数或进一步结合Biot 模型[18-19]和Biot-Stoll模型[20]开展底质分类研究。其中，Biot[21]将底质假设为由固体颗粒和孔隙流体组成的多孔弹性介质，考虑了孔隙流体在底质颗粒孔隙内的粘滞运动，解释了声波传播及损失的原因。Stoll[22]在Biot 理论基础上，进一步将孔隙流体中的声波与固体颗粒骨架中的压缩波与剪切波耦合，形成了快压缩波、慢压缩波和剪切波等三种波。Biot-Stoll 模型具有较为完备的物理基础，被广泛用于描述底质声学、物理、力学性质之间的关系[23-26]，底质的声学特性与其软硬、粗细、松密密切相关[27]，但目前，基于Biot-Stoll模型的底质反演研究多考虑粒径粗细[23-26]，鲜有关注松密的影响。

因此，本文首先给出从浅地层剖面数据中提取海底反射系数的方法，然后通过引入相对密度得到考虑底质松密影响的改进Biot-Stoll 模型，将二者结合构建海底反射系数与底质平均粒径之间的关系进行底质反演，最后基于实际算例初步验证了本文方法的有效性。

1 基于浅地层剖面数据提取海底反射系数

1.1 浅地层剖面探测原理

浅地层剖面仪发射的低频声波以近似垂直的方式入射到达海底，部分声波在海底面反射，部分声波穿透海底面进入沉积层内部并在不同层面处发生反射（图1），接收换能器按照各反射界面阻抗特性和深度的不同收到回波。通过对这些回波数据进行滤波、放大等处理，从而获取水下浅部地层结构、构造和沉积物特征[11]。

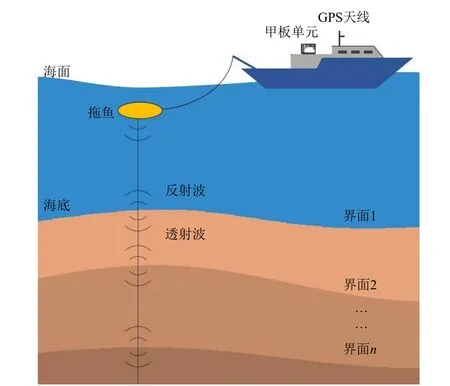
图1 浅地层剖面探测原理Fig.1 Principle of sub-bottom profiling

1.2 浅地层剖面数据读取

浅地层剖面原始记录携带了海底面及沉积层内部信息，根据其数据结构[28]，在Matlab 环境下编程读取SEGY 格式文件中解析信号形式的海底回波振幅信息。然后，以每条测线的Ping 值作为行向量，每Ping 采样点数作为列向量存储回波信息。

1.3 海底反射系数提取

声波在海水-海底界面反射的强弱由海底反射系数表征。通常来说，相对粗糙和坚硬的岩、砾，比沙、泥的声反射更强，其海底反射系数也更大，因此，海底反射系数常被用于底质分类[29]。海底反射系数R可通过下式计算：

式中，Ar为反射波振幅，通过对海底反射波频谱分析，取中心频率的振幅获得；Ai为入射波振幅，对基于Chirp信号的浅地层剖面数据，可通过有效声压代替[15]：

式中，Peff为有效声压强度（Pa），SPL 为发射信号的声源级（dB），Pref为海水中参考声压强度，表层海水取10-6Pa。假设海水均匀，在不考虑海水的吸收损失的情况下，需要对海底反射波进行球面扩散补偿[30]，海底反射系数计算公式可进一步表示为[15]：

式中，海水声速Vw取1 500 m/s，T为反射波的双程走时（s）。

以一条测线的浅地层剖面记录为例，提取海底反射系数流程如下：

（1）识别海底位置。搜索每Ping 数据中的海底反射振幅，根据浅地层剖面图像和海底的连续性识别海底，具体方法为：搜索每Ping 数据中的最大值，作为海底的预估位置；取前三Ping 预估位置的平均深度为基准值，将下一Ping 预估值与基准值做差，若小于100、则选用，若超过100、则以基准值代替预估值；依次校正，最终确定该条测线所有海底位置。

（2）提取反射波振幅。根据已确定的海底位置，从浅地层剖面原始记录中提取对应的海底反射信息并进行频谱分析，得到反射波中心频率（8.5 kHz）处的振幅信息。

将振幅信息和走时代入公式（3）得到某典型测线的海底反射系数见图2 所示，反射系数主要位于0.1～0.5 区间、滑动平均值为0.12～0.25，与实测[31]及基于浅地层剖面数据提取[19-20,24]的反射系数范围相一致，并且沿测线呈现出一定的变化特征，表明了本文结果的可靠性和方法的可行性。

图2 基于浅地层剖面数据计算得到的某测线海底反射系数Fig.2 Sea bottom reflection coefficients of a survey line calculated from SBP data

2 改进孔隙度计算

2.1 Biot-Stoll 模型

Biot[21]将底质假设为一种由孔隙流体和固体颗粒构成的多孔弹性介质，描述了声波在多孔介质中的传播规律。Stoll[22]在Biot 模型基础上，定义了H、C、M三个模量来表征颗粒骨架的弹性和非弹性响应，并结合动力方程推导出快、慢两种纵波在多孔介质中的传播方程：

式中，H表示弹性模量，e表示骨架应变，C为附加弹性模量，ϛ为流入或流出的液体体积（m3），t是时间（s），ρ和ρf分别是底质密度和孔隙流体密度（kg·m-3），M表示复弹性模量，η是孔隙流体粘滞系数（kg·m-1·s-1），к是渗透率（m2），m是宏观压力梯度下流体流动的相位，计算公式为：

式中，Г为弯曲度，n为底质孔隙度（%）。

2.2 孔隙度计算

孔隙度是影响底质压缩声速变化的重要参数[32]，对Biot-Stoll 模型计算结果影响显著[21-22]，其计算公式为：

式中，ρs为颗粒密度（g·cm-3），Sr为饱和度（忽略浅层气影响、即海床完全饱和的情况下，Sr取为1）。可以看出，当前公式主要通过体积密度、颗粒密度和孔隙流体密度计算孔隙度，实测的沉积物孔隙度[33]普遍大于公式（7）计算得到的理论值。相对密度表征无黏性底质的松密程度，对其性质有重要影响，因此，本文引入相对密度对公式（7）进行改进：

式中，Dr为相对密度，a为相对密度改正系数，由基于状态可控试验的实测数据[33]获取，该实验以相对密度为控制变量制备不同状态的砂土和粉土试样，使用超声探测仪进行压缩波速和物理性质测试。Dr计算公式为：

式中，nmax和nmin分别为最大、最小孔隙度（%），参照文献[34-37]给出不同平均粒径条件下的取值（表1）。根据表1 中不同粒径条件下的nmax、nmin和表2 中的实测孔隙度n计算得到Dr，利用最小二乘法得到孔隙度计算值与实测值均方根误差最小时的改正系数a=0.036 6。

表2 状态可控试验实测数据[33]Table 2 Measured physical parameters of state-controlled experiments

2.3 海底反射系数与平均粒径关系

本文通过Biot-Stoll 模型计算不同平均粒径底质的声速，进而得到反射系数与平均粒径的关系。Biot-Stoll 模型共有13 个参数，Stoll[22]通过测试，分别给出了泥和砂两种底质的参数取值方法，Schock[18]进一步将渗透率、弯曲度、孔隙半径等参数函数化并给出计算表达式，陈静[38]则证明Schock 参数的计算效果更好。

本文底质密度ρ（g·cm-3）由Hamilton[33]经验公式估算：

其中，Ф为底质平均粒径，其他参数参照文献[18,22,38]中的经验值或经验公式获取，详见表3。

表3 Biot-Stoll 模型参数取值Table 3 The input physical parameters of the Biot-Stoll model

底质孔隙度n则分别根据公式（7）和公式（8）计算，将运用引入相对密度影响的孔隙度计算公式（8）的Biot-Stoll 模型称为“改进Biot-Stoll 模型”。将上述参数输入Biot-Stoll 模型，计算得到底质声速Vp（m·s-1），再代入下式求取海底反射系数[39]：

计算得到的海底反射系数R与平均粒径的关系如图3 所示，平均粒径随R的增大而减小，并且平均粒径相同时，改进Biot-Stoll 模型得到的R更小。

图3 海底反射系数与平均粒径的关系a: Biot-Stoll 模型；b: 改进Biot-Stoll 模型。Fig.3 The relationship between reflection coefficient and mean grain sizea: Biot-Stoll model; b: Modified Biot-Stoll model.

3 实例验证

3.1 研究区概况与数据获取

在山东省威海市北部海域获取实测数据，水深20～70 m，等深线走向与海岸线近似平行（图4）。使用Edgetech 3100P 浅地层剖面仪进行数据采集，设备声源级202 dB，采样频率21 701 Hz，每Ping 采样点数2 604，Chirp 信号频率2～15 kHz、中心频率8.5 kHz、脉冲宽度20 ms，主测线间距60 m，检查线与主测线垂直（图4）。同时，在测区使用DDC1 型蚌式取样器采取底质样品12 组，取样点在测区均匀布置，取样深度10～30 cm，每站取样量不少于300 g。在实验室内使用筛分-沉降法测试得到底质样品的粒径级配曲线及平均粒径。

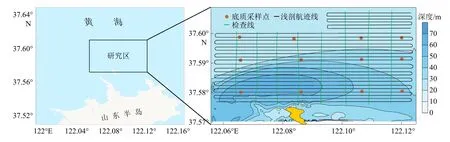
图4 研究区位置及浅地层剖面航迹线和底质取样站位Fig.4 The study area and the deployment of the sub-bottom profiler track lines, and sediment sampling stations (red dots)

3.2 反演结果分析

按照第1 节方法得到每条测线各Ping 的海底反射系数，用克里金插值得到研究区内反射系数分布（图5），从中按照12 个取样点坐标提取对应海底反射系数，按照第2 节方法反演得到海底底质平均粒径，与取样点实测平均粒径进行对比。如表4 所示，改进Biot-Stoll 模型反演结果与实测平均粒径的相对误差为0.41%～15.13%，总体误差水平较低。并且，改进模型反演12 个底质点中的9 个相对误差比传统模型有所降低，相对误差平均值也从6.51%降至5.06%，提升了底质反演精度。

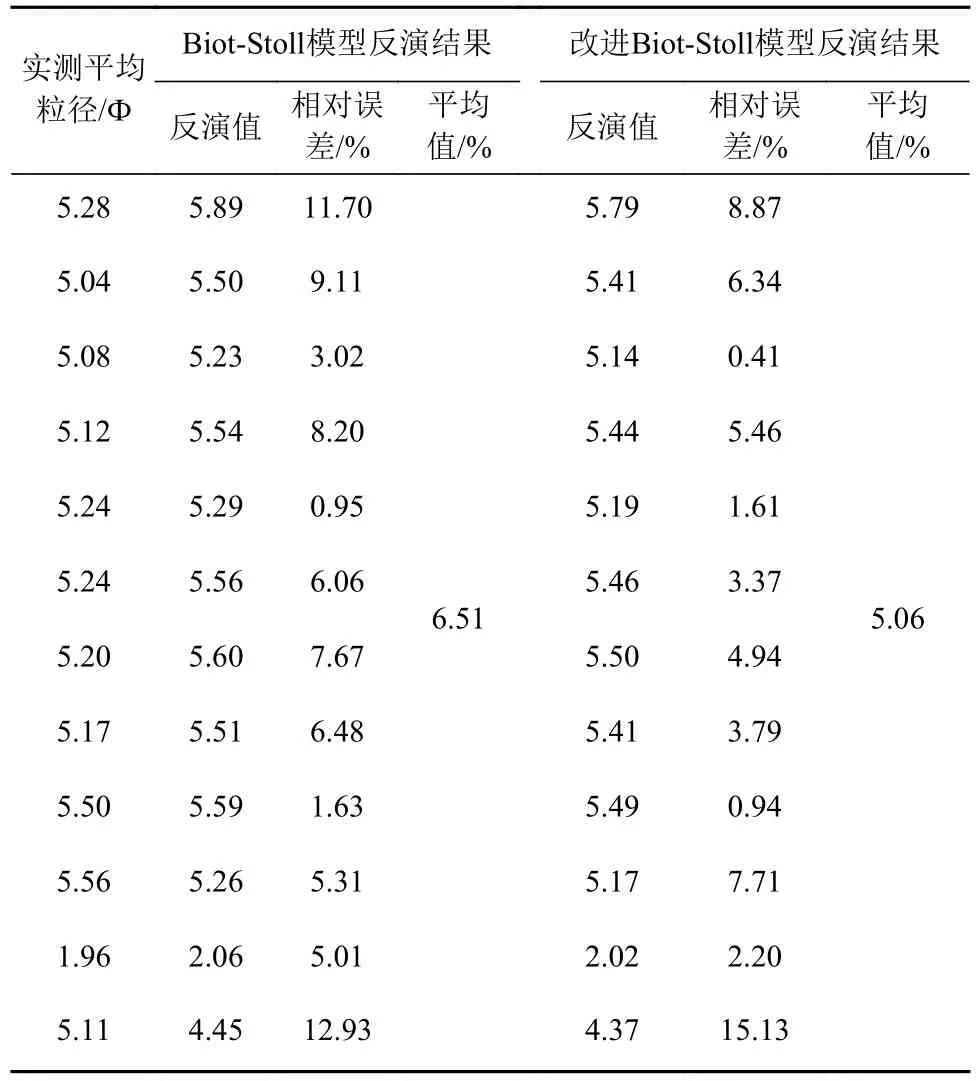
表4 地声反演与实测结果比较Table 4 Comparison between inversion and measured mean grain-size

图5 研究区反射系数分布图Fig.5 Distribution of reflection coefficients in the study area

为进一步验证本文改进Biot-Stoll 模型的底质反演效果，从文献[19-20,40]的浅地层剖面数据中提取海底反射系数以及实测平均粒径数据进行计算，从表5 可以看出，改进Biot-Stoll 模型在传统Biot-Stoll 模型基础上将反演值与实测值的平均相对误差从29.69%降到了27.22%，并提升了所有21 个点中的20 个点的底质反演精度。所以，基于实测数据和文献数据的算例结果显示出本文改进Biot-Stoll 模型进行底质反演对于不同区域、不同底质类型具有较好的适用性。

表5 地声反演与文献结果比较Table 5 Comparison between inversion results and those from published sources

海底底质由固体颗粒和孔隙水组成，声波在固体颗粒中的传播速度比孔隙水的传播速度更快，同一种底质其相对密度越大、固体颗粒排列越紧密，则声波传播的有效路径越短，因而表现出相对较大的宏观声速，进而影响海底反射系数。相对密度比体积密度更好地表征了底质的松密程度，正是基于此物理基础，本文引入相对密度改进对孔隙度计算公式，形成改进Biot-Stoll 模型并提升了底质反演精度。