纤维增强复合材料的仿生结构设计及其力学性能的数值模拟
2024-02-22席凯凯
席凯凯,葛 鹏,杨 楠
(西部金属材料股份有限公司,陕西 西安 710000)
自然界的天然生物复合材料具有优良的力学性质,如木和竹等,到目前为止,对天然物复合材料的仿生学研究已经取得了一系列进展[1-7]。陈斌、陈锦祥等[8-11]在金龟子的外甲壳中发现了双螺旋铺层结构和纤维绕孔铺层结构,并分析了纤维铺层对金龟子鞘翅强韧化机制的影响;韩奇钢[12]等设计了一种仿螳螂虾前锤玄武岩纤维增强复合材料模型,其抗载荷能力比非螺旋复合材料提升了28.9%;陈昊宇[13]等采用3D打印技术制备了一种螺旋铺层仿生复合材料,其弯曲性能和失效形式均优于传统铺层结构;王瑜[14]等基于Bouligand结构设计了一种仿生螺旋复合材料结构,发现螺旋角对试样的断裂韧性有很大的影响。
在对纤维增强复合材料的模拟和实验中,大多将纤维的尺寸取为一致,且对纤维增强复合材料结构表面摩擦性能的研究较少。研究表明,通过对纤维增强复合材料进行合理的结构和铺层设计后,其吸能性能、轻质特性和表面耐磨性能将比金属材料更加优越[15]。生活在河流、湖泊里的淡水龙虾和螃蟹都有掘洞的生活习性[16],在捕食、逃逸和掘洞时,螯发挥着重要作用,这就要求螯具有高强和轻质特性,其表面还应具备耐磨减阻和脱黏的特性,这样才能加快其移动速度、掘洞速度和螯的使用寿命。因此,淡水龙虾和螃蟹螯是一种优良的仿生原型。本文从仿生学角度出发,将淡水龙虾和螃蟹螯经过亿万年进化而来的优良结构运用于纤维增强复合材料的结构设计,并利用有限元模拟的方法对设计的纤维增强复合材料模型进行了抗压性能、抗扭性能、吸能性能和表面摩擦性能等方面的分析。
1 淡水龙虾和螃蟹螯表面及断面微观结构
吴志威[16]对淡水龙虾和螃蟹螯进行前期的物理和化学处理后,利用SEM观察到两者的螯表面均呈非光滑形态[17]。淡水龙虾和螃蟹螯外骨骼层分为内、外表皮层,均由螺旋夹板层[18-20]堆栈而成,螺旋夹板层由壳质-蛋白纤维面绕着法线方向旋转180o叠积而成[16]。淡水龙虾外骨骼断面的螺旋夹板层上密布着小孔,小孔上残留着小管道(图 1(b));淡水螃蟹螯断面内表皮层的螺旋夹板层间隔较大,没有外表皮层致密(图2(b)(c)),外表皮层螺旋夹板层厚度大约是内表皮层的2~3倍,同样在孔道里贯穿着狭长的小管道[16]。
2 建立纤维增强复合材料细观模型
基于前人的观察和研究,本文在前人研究的基础上提出一种纤维增强复合材料模型,如图3所示。
本文从四个生物学特征出发进行纤维增强复合材料的仿生结构设计:(1)用加强纤维来模仿生物材料中的壳质-蛋白纤维;(2)用加强纤维的多角度排列来模仿生物材料中小管道的各向异性排列;(3)用加强纤维的多层排布来模仿生物材料中的分层特性;(4)螺旋夹板层由壳质-蛋白纤维构成,因此用加强纤维在纵向的尺寸差异来模仿生物材料内外表皮层螺旋夹板层厚度的差异。
3 纤维增强复合材料模型的数值模拟
3.1 复合材料模型力学性能的研究
为了探究加强纤维在基体中的作用以及加强纤维的螺旋排列方式在基体中的作用,利用三维软件分别建立了无纤维模型、平行纤维模型和螺旋纤维模型(图4),螺旋纤维模型排列角度为 30o,将上述模型导入ANSYS Workbench中进行抗压和抗扭等方面的数值模拟分析。
3.1.1 求解
(1)材料参数设置。加强纤维选择E-玻璃纤维,基体选择树脂基基体[16],具体的材料参数为,树脂基体弹性模量3 400 MPa,泊松比0.35;E-玻璃纤维弹性模量76 000MPa,泊松比0.30。
(2)有限元网格划分。将基体与加强纤维的单元类型均设置为六面体单元,网格单元总数为766 617,网格划分效果如图5所示。
(3)载荷设置。在垂直于纤维面的y 方向上(图5)施加400 N压力载荷,对四个侧面添加固定约束。
3.1.2 模拟结果定性分析
图6为三种纤维模型切面的压缩变形云图。从图中可以看到,无纤维模型的大变形区域范围较广,平行纤维模型和螺旋纤维模型的大变形区域范围较小,且两者的变形区分布相似。模拟数据表明,无纤维模型最大变形量为2.64×10-6m,平行纤维模型最大变形量为1.41×10-6m,螺旋纤维模型最大变形量为1.35×10- 6m;无纤维模型最大压缩变形能为6.41×10-8J,平行纤维模型最大压缩变形能为4.22×10-8J,螺旋纤维模型最大压缩变形能为3.15×10-8J。对比无纤维模型与平行纤维模型的最大变形量和最大变形能可以得出,在基体中加入纤维,可以提高整个复合材料模型的抗压性能和吸能性能。对比平行纤维模型和螺旋纤维模型的最大变形量和最大变形能可以得出,基体中纤维的各向异性排列可以提高整个复合材料模型的抗压性能和吸能性能。因此在法向载荷作用下,螺旋纤维模型抗压能力最强、吸能效果最好,平行纤维模型次之,无纤维模型最差。
在xoz面上施加400 N·m的扭矩,扭矩平行于纤维面,施加载荷面的对面设置为固定约束。图7为三种纤维模型切面的扭曲变形云图。从图中可以看到,三种纤维模型的变形区域都沿着xoz面自上而下逐渐变小,且无纤维模型的大变形区域范围更大,平行纤维模型和螺旋纤维模型的大变形区域范围较小,且两者的变形区分布相似。模拟数据表明,无纤维模型的最大变形量为4.30 mm,平行纤维模型的最大变形量为2.30 mm,螺旋纤维模型的最大变形量为2.37 mm;无纤维模型的最大扭曲变形能为3.1 mJ,平行纤维模型的最大扭曲变形能为2.5 mJ,螺旋纤维模型的最大扭曲变形能为2.1 mJ。因此,在基体中加入纤维并改变纤维的排列方向,可以提高整个复合材料模型在平行纤维面方向的抗扭性能和吸能性能。
另外,在xoy面上施加400 N·m的扭矩,扭矩垂直于纤维面,施加载荷面的对面设置为固定约束。模拟数据表明,无纤维模型的最大变形量为4.23 mm,平行纤维模型的最大变形量为2.66 mm,螺旋纤维模型的最大变形量为2.53 mm。因此,在基体中加入纤维并改变纤维的排列方向,可以提高整个复合材料模型在垂直纤维面方向的的抗扭性能。
3.1.3 模拟结果分析
(1)变形量的理论分析。首先对无纤维模型和平行纤维模型的变形量进行理论对比分析。平行纤维模型中贯穿着大量的玻璃纤维,由于玻璃纤维的弹性模量很高,受力后的变形量非常小,所以当基体受到同样大小的作用力时,平行纤维模型在受力方向上的变形量也就比无纤维模型小(图6(a)(b)对比)。同理,当基体受到同样大小的横向或纵向扭矩作用力,平行纤维模型的变形量总比无纤维模型小。
其次对平行纤维模型和螺旋纤维模型的变形量进行理论对比分析。两种纤维模型的差异在于纤维的各向异性排列,这种各向异性排列的差异可以分解为横向的各向异性差异和纵向的各向异性差异,如图8和图9所示。由图8可知,平行纤维模型的纤维排布只有一个方向,而螺旋纤维模型的纤维排布具有多个方向,如果基体受到垂直于纤维面的载荷时,平行纤维模型只能将这个载荷沿一个方向传递下去,容易使该方向产生大变形,而螺旋纤维模型可以将该载荷沿多个方向进行分解,改变应力分布状态,使应力分布均匀化,减少沿初始载荷方向产生的变形量。因此,当基体受到垂直于纤维面的法向压力载荷和扭矩载荷时,螺旋纤维模型的变形量总比平行纤维模型小。由图9可知,平行纤维模型和螺旋纤维模型在纵向的各向异性差异并不明显,当基体受到平行于纤维面的载荷时,平行纤维模型和螺旋纤维模型的变形量基本一致。因此,应该对螺旋纤维模型在纵向的排布进行优化,使其在纵向具有各向异性,来减少平行于纤维面的载荷产生的变形量。
(2)变形能的理论分析。随着基体表面载荷的施加,纤维-基体界面将发生如下过程,纤维端部脱黏—脱黏区沿界面向纤维中部延伸—脱黏区进一步扩展—纤维端部界面发生相对滑移[21]。在第四个过程中,界面径向应力导致的摩擦力将阻止纤维沿界面的滑移,当基体表面载荷增加至界面摩擦力不足以抑制纤维滑移时,界面端部将产生滑移,导致纤维从基体界面拔出,使材料产生破坏。
当产生界面滑移时,平行纤维模型的纤维排布只有一个方向,因此只需要拔出该方向的纤维,就可以使平行纤维模型产生破坏,因此本文重点分析螺旋纤维模型。
首先,螺旋纤维模型的纤维排布遍布整个圆周,拔出需要耗费大量的能量;其次,螺旋纤维模型中纤维与基体的接触面积更广,增加了拔出阻力,提高了断裂韧性;最后,螺旋纤维的各向异性排列,改变了材料内部载荷的传递过程,使应力的分布更加均匀,提高了材料的吸能性能。
3.2 加强纤维排列角度对复合材料模型性能的影响
为了探究加强纤维排列角度对复合材料模型力学性能的影响,在三维软件Solidworks中建立了不同排列角度的螺旋纤维模型,然后导入ANSYS Workbench中进行抗压和抗扭等方面的数值模拟分析。
分别对上述模型施加400 N的压力载荷、400 N·m的平行纤维面扭矩、400 N·m的垂直纤维面扭矩。图10为螺旋纤维模型的最大压缩变形量随排列角度的变化曲线,图11为螺旋纤维模型的最大压缩变形能随排列角度的变化曲线,图12为螺旋纤维模型受横向扭矩和纵向扭矩作用后的最大变形量随排列角度的变化曲线,图13为螺旋纤维模型受横向扭矩和纵向扭矩作用后的最大变形能随排列角度的变化曲线。
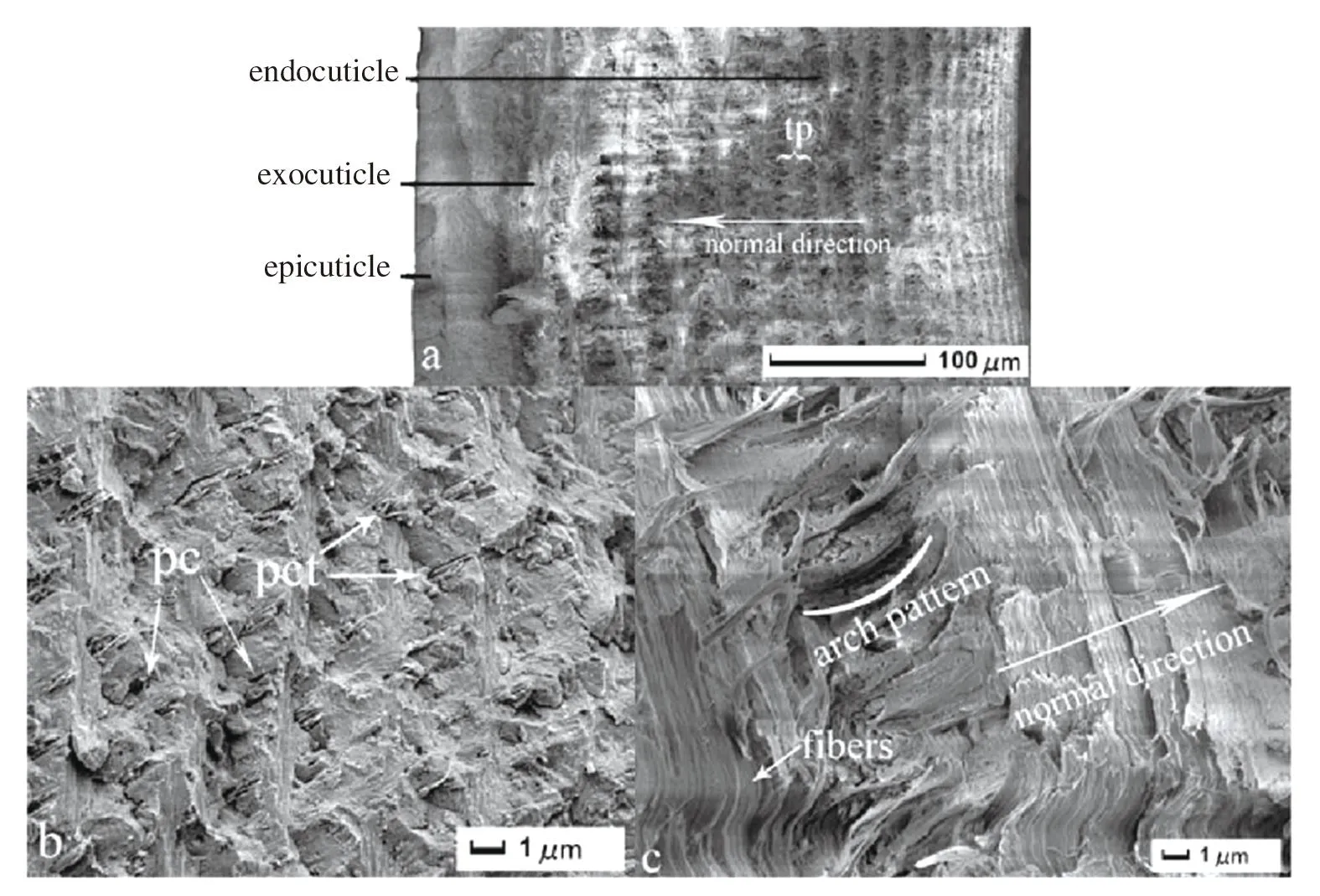
图1 淡水龙虾螯断面微观结构

图2 淡水螃蟹螯断面微观结构

图3 纤维增强复合材料细观模型
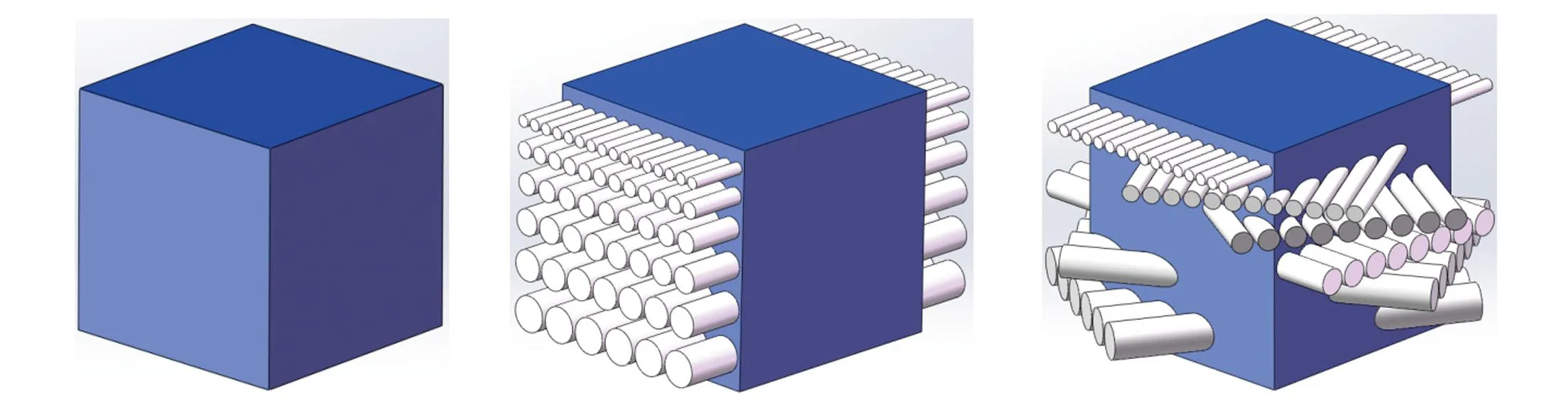
(a)无纤维模型 (b)平行纤维模型 (c)螺旋纤维模型图4 分析模型

图5 网格划分效果图
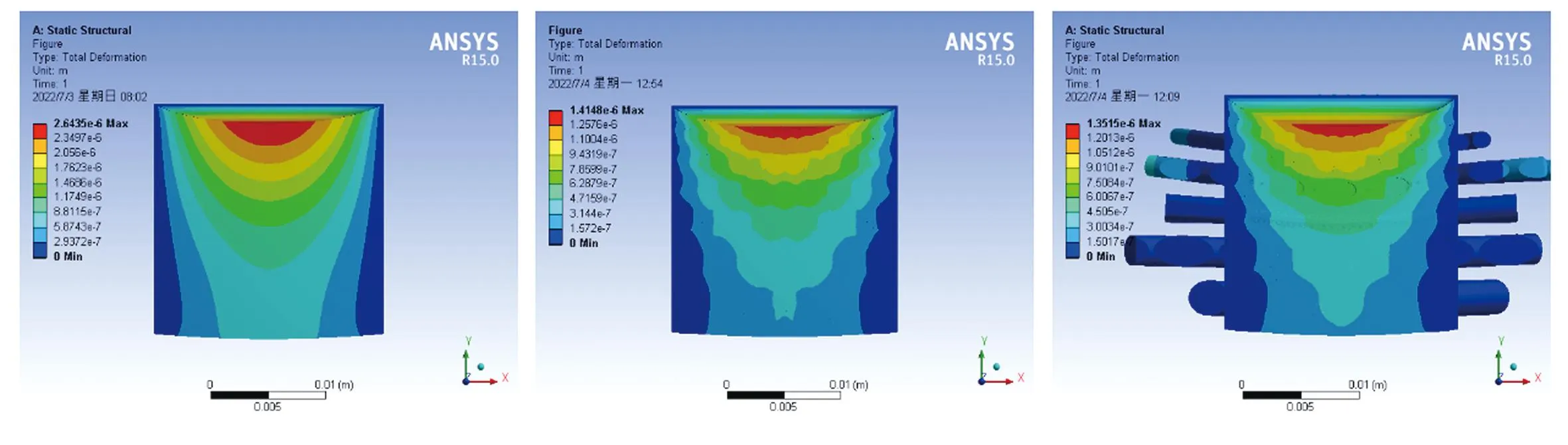
(a)无纤维模型 (b)平行纤维模型 (c)螺旋纤维模型图6 分析模型的压缩变形云图
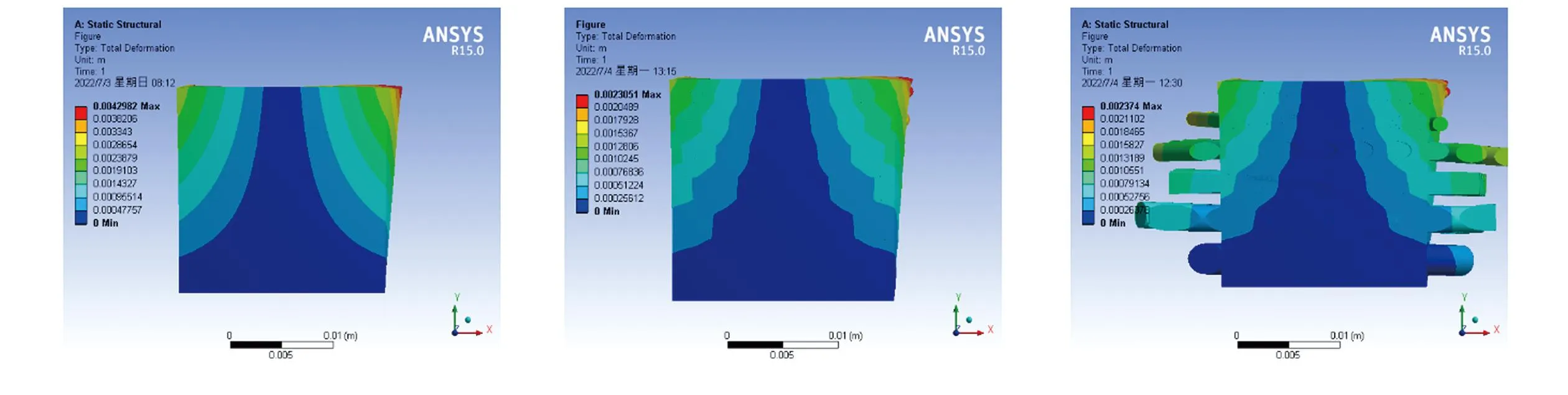
(a)无纤维模型 (b)平行纤维模型 (c)螺旋纤维模型图7 分析模型的扭曲变形云图

(a)平行纤维模型 (b)螺旋纤维模型图8 横向的各向异性差异

图10 最大压缩变形量随排列角度的变化曲线 图11 最大压缩变形能随排列角度的变化曲线

图12 最大变形量随排列角度的变化曲线 图13 最大变形能随排列角度的变化曲线
从图中可以看到,随着纤维排列角度的增加,螺旋纤维模型的最大变形量和最大变形能都在减小,模型的抗压性能、抗扭性能和吸能性能都在逐渐提升;随着纤维排列角度的增加,能量吸收机制由基体控制向纤维与基体共同控制转化,模型的吸能性能逐渐增强。
3.3 复合材料模型厚度方向力学性能的研究
由于复合材料模型每一层纤维的直径均不一致,导致复合材料模型内外表层附近的力学性能也就不一致。为此,本文对复合材料模型的内外表层分别进行抗压性能、抗扭性能和吸能性能的数值模拟分析,复合材料模型选择平行纤维模型,并选择各层纤维直径一致的复合材料模型作为对照组,且所有模型中纤维的总体积相等。
分别对平行纤维模型的内表层、外表层以及均匀纤维模型内表层施加400 N压力载荷、400 N·m的平行纤维面扭矩、400 N·m的垂直纤维面扭矩。图14为平行纤维模型内外表层及均匀纤维模型内表层的切面压缩变形云图,表1和表2记录了相关变形量数据和变形能数据。结合图14和表1数据可以看到,平行纤维模型外表层的压缩变形量最小,平行纤维模型内表层次之,均匀纤维模型内表层最大;横/纵向扭矩变形量也是平行纤维模型外表层最小,平行纤维模型内表层次之,均匀纤维模型内表层最大。因此,相比均匀纤维模型,将纤维的尺寸设置为一定的梯度,可以增强纤维模型的抗压性能和抗扭性能,且纤维尺寸越大,模型的抗压性能和抗扭性能越好。从表2数据可以得到,将纤维的尺寸设置为一定的梯度,可以增强纤维模型的吸能性能,且纤维尺寸越大,模型的吸能性能越好。
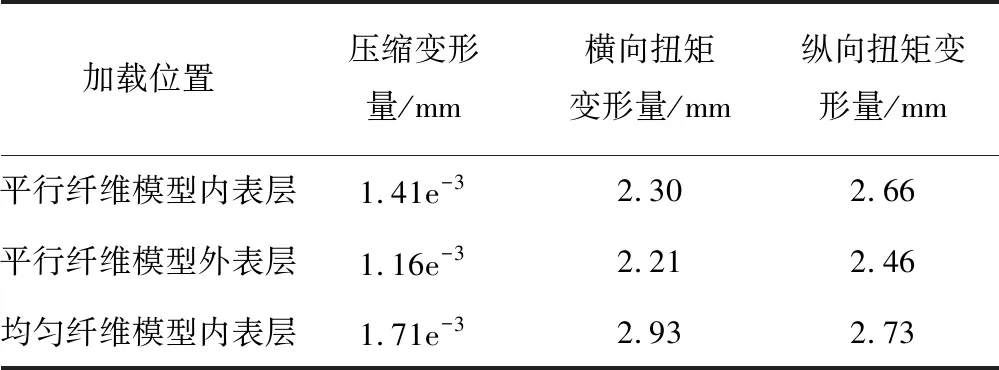
表1 不同位置的最大变形量
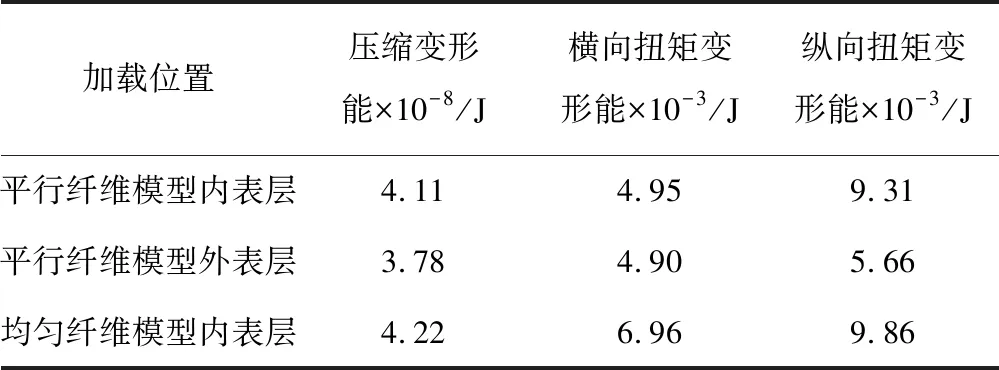
表2 不同位置的最大变形能

(a)平行纤维模型内表层压缩变形 (b)平行纤维模型外表层压缩变形 (c)均匀纤维模型内表层压缩变形图14 压缩变形云图
3.4 复合材料模型表面摩擦性能的研究
淡水龙虾和螃蟹螯表面呈非光滑形态。相关研究表明,非光滑表面可以减小黏附、降低摩擦阻力[22-24],淡水龙虾和螃蟹螯表面是否具有耐磨减阻的特性对其掘洞速度以及螯的使用寿命都具有重要意义。
3.4.1 摩擦分析模型的建立
为了探究淡水龙虾和螃蟹螯表面的凹坑和凸起是否具有耐磨减阻特性,本文在螺旋纤维模型(30o)的内表层布置了凹坑形仿生单元体。在此模型中,非光滑度(宏观)是指凹坑形仿生单元体的面积占螺旋纤维模型内表层面积的百分比。根据前人研究,仿生单元体直径为2 mm、非光滑度为12.5%、仿生单元体采用均匀排布方式时耐磨减阻效果最好[25-27],按照上述经验,将凹坑形仿生单元体排布在螺旋纤维模型的内表层,如图15所示,并将光滑内表层的螺旋纤维模型设置为对照组。将上述模型的内表层分别与花岗岩平板进行紧密接触,组成摩擦分析模型,然后导入Abaqus进行数值模拟分析。

图15 凹坑形仿生单元体排布图
3.4.2 材料参数设置
相关材料参数见表3。

表3 材料参数表
3.4.3 求解设置
在螺旋纤维模型外表层施加100 N的压力载荷,内表层与花岗岩之间的接触采用摩擦接触,摩擦因数为0.25;让螺旋纤维模型做水平向右的直线运动,速度0.2 mm/s;将花岗岩平板的底面设置为完全固定约束;仿真时间设置为5 s。
3.4.4 模拟结果分析
图16为两种分析模型内表层的等效应力云图,图17为两种分析模型内表层摩擦力随时间变化曲线图。从图中可以了解到,螺旋纤维模型非光滑内表层的最大等效应力是光滑内表层的0.74倍,非光滑内表层摩擦力的平均值是光滑内表层的0.53倍,由此可见,螺旋纤维模型非光滑内表层的确具有耐磨减阻的作用。一方面,由于螺旋纤维模型中纤维的各向异性排列,使得外表层传递到内表层的应力在内表层各个位置的分布均不一致,传递到内表层的应力作用在非光滑单元体上,使得这些单元体与花岗岩接触部位附近的摩擦力发生变化;另一方面,凹坑型表面有效减少了接触区域的面积,具有脱黏作用。
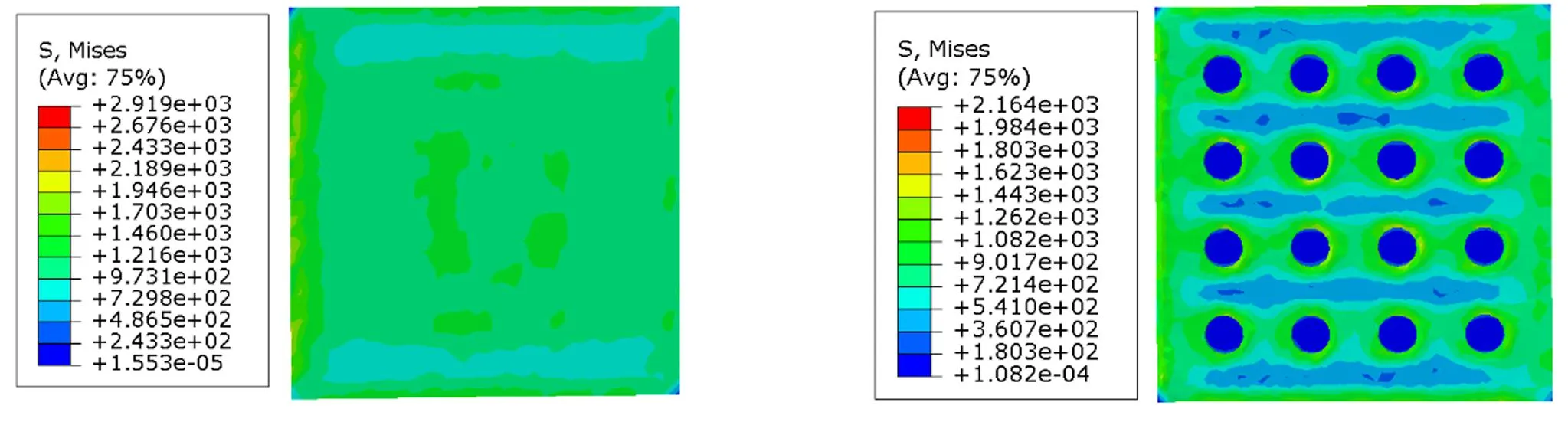
(a)螺旋纤维模型光滑内表层 (b)螺旋纤维模型非光滑内表层图16 两种分析模型内表层的等效应力云图
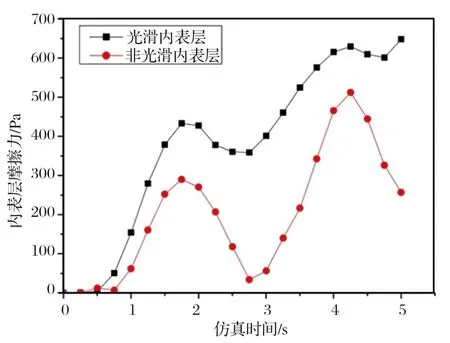
图17 两种分析模型内表层摩擦力随时间变化曲线图
综合以上分析,淡水龙虾和螃蟹螯内部结构与其表面的非光滑形态相互配合,使其表面具有耐磨减阻和脱黏的功效。
4 结论
(1)在基体中加入纤维以及纤维的各向异性排列均可以提高纤维增强复合材料模型的抗压性能、抗扭性能和吸能性能。
(2)随着纤维排列角度的增加,复合材料模型的抗压性能、抗扭性能和吸能性能都在逐渐提升。
(3)将纤维的尺寸设置为一定的梯度,可以增强复合材料模型的抗压性能、抗扭性能和吸能性能。
(4)淡水龙虾和螃蟹螯表面的非光滑形态具有耐磨减阻和脱黏的功效。
(5)应对螺旋纤维模型在纵向的排布进行优化,使其在纵向具有各向异性,来提高横向的抗扭性能。
