电动飞机电推进锥形永磁同步电机轴向磁拉力影响因素分析
2024-02-21梁力豪梁培鑫樊昱琨刘澄林
梁力豪,梁培鑫,樊昱琨,刘澄林
西北工业大学,陕西 西安 710129
传统飞机造成的环境及噪声污染日益严重[1-2],为解决上述问题,零排放、低噪声的电动飞机引起了越来越多国家的关注[3-5]。与传统的涡轮螺旋桨飞机不同,电动飞机使用带有螺旋桨的电动机为飞机提供动力。美国电气设备服务协会(EASA)结合飞机维修技术人员的反馈总结出了电动飞机的维修注意事项,强调电动飞机中螺旋桨轴向力、振动等因素导致电机轴承磨损严重,尤其在飞机起飞阶段螺旋桨受力更大,对轴承损害更为严重[6]。由于螺旋桨与电机轴直接相连,在飞机飞行的过程中,螺旋桨旋转产生的推力通过电机轴承传递给机身。长期按此方式运行,会造成电推进电机轴承的磨损,缩短飞机的运行寿命,甚至会产生安全隐患[7-8]。
为了降低电动飞机的安全风险和减小轴承处的受力磨损,本文采用锥形永磁同步电机(CR-PMSM)自身产生的轴向磁拉力来平衡轴承处的受力。考虑到不同的飞行工况,锥形电机轴向磁拉力的计算,对于实现轴承处受力的有效平衡尤为重要。目前,计算轴向力的方法有虚位移法、麦克斯韦应力法和有限元法。虚位移法是假设转子移动一个很小的位移,定转子气隙能量变化对轴向位移求导获得轴向力,但该方法忽略了谐波的影响[9-10]。麦克斯韦应力法认为轴向力密度与气隙磁密的平方成正比,轴向力等于轴向力密度的面积分[11-12]。有限元法利用微元的方法计算各剖分单元的轴向力,然后再对整个求解区域求和[13-14]。相对而言,麦克斯韦应力法和有限元法,计算精度更高,较为常用。
本文基于磁路法和磁场解析法,构建了锥形电机的转子磁路解析模型,计算了锥形转子磁路的相关参数,并根据张力张量法,给出了锥形电机轴向磁拉力的计算公式,着重分析了锥形电机特有的结构参数,即锥角及交直轴电流对轴向磁拉力的影响规律,最后通过仿真验证了该分析模型的正确性和有效性,为后续锥形电机的分析提供了理论参考。
1 CR-PMSM轴向磁拉力数学模型
本文以8 极54 槽内置式CR-PMSM 为例,其整体结构及定转子如图1所示。

图1 锥形电机模型Fig.1 CR-PMSM model
电机通过前端盖与法兰盘相连,实际安装时,电机轴通过键与联轴器紧密配合,螺旋桨固定在联轴器上。图1(a)中标号含义如下,构成转子的组成部分有:转轴(1)、转子(2)和永磁体(6);构成定子的部分有:定子铁芯(3);构成电机机壳的部分有:深沟球轴承(15,16),机壳(5),后端盖(4),前端盖(7);构成前端轴向力测量的部分有:防尘保护套筒(9)、螺旋桨固定轴承(11)、定位轴承套(12)、S形压力传感器(13);构成法兰盘组件的有:前端固定法兰盘(8)、法兰盘紧固件(14)、法兰盘底座(17)、螺旋桨(10)。
由于锥角的存在,锥形电机定转子间的磁拉力可分解为径向力和轴向力,如图1(b)所示。其中,该轴向分力可用来平衡螺旋桨的轴向力。相较于同结构的柱形电机,锥形电机在抵消螺旋桨轴向力、保护轴承方面具有明显优势。同时,锥形电机的电磁性能与柱形电机相差不大,为了验证此观点,仅以锥角为变量,在相同转速、电流下,电机的电磁转矩随锥角的变化如图2所示。锥角为0°时,电机为柱形电机,随着锥角变化,转矩变化不大。本文中锥形电机的锥角为7°,其轴向力与柱形电机(锥角为0°)的转矩差异仅为1.66%。由此可见,在合理的锥角变化范围内,锥形电机电磁性能与柱形电机相差不大,同时锥形电机又具有平衡螺旋桨轴向力的优势。
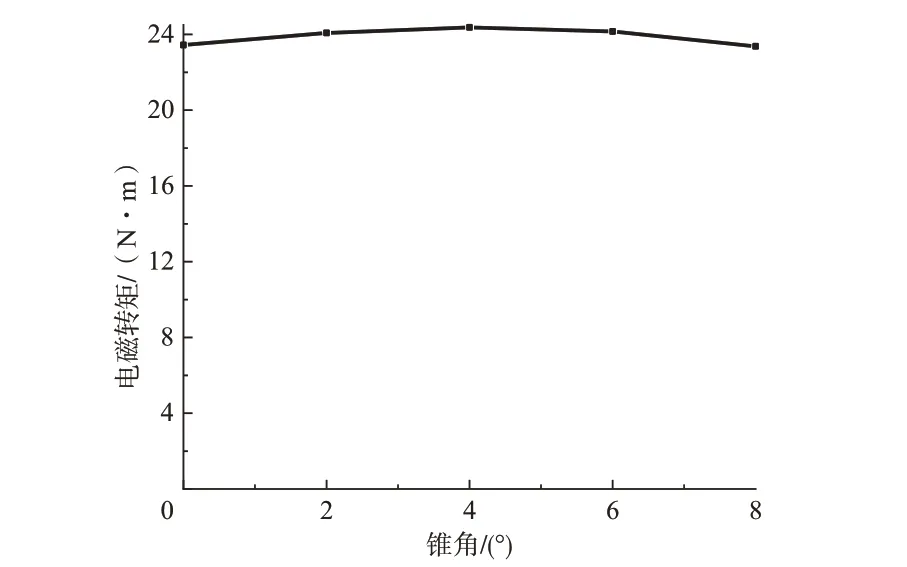
图2 锥角对电磁转矩的影响Fig.2 The influence of cone angle on electromagnetic torque
由于锥形电机沿轴向各个截面形状不一,解析难度较大,分析时常将各个不同截面等效为柱形进行等效分析。分析锥形电机转子磁路时,多选取转子轴向长度中点截面进行计算。为提高模型精度,本文将内置式CR-PMSM按轴向等分为n个单元,每个单元分别等效为内置式柱形永磁同步电机(PMSM),建立每个单元磁路模型[15],并对上述模型进行磁路分析,求解气隙磁密。最后用张力张量法及转子表面微元积分,结合转子锥角,给出电机轴向磁拉力解析式。
1.1 CR-PMSM等效磁路模型
图3为电机轴向等分后,第1份等效柱形电机剖面示意图。其中,wm_in为永磁体宽度,lm_in为永磁体厚度,l为电机轴向长度,rs_in为定子内径,rr_in为转子外径,rr_av为转子外圆中间端面平均半径,p为极对数,wb_in为磁桥宽度,μBb为磁桥磁导率,tb为磁桥厚度。由于目标电机转子外径及定子内径相对电机轴所成锥角较小,为保证建模精度,本文将电机按转子轴向长度等分为n份。本文电机齿、轭饱和程度较低,故根据磁路法可得电机等效磁路模型如图4所示。图4中,Rg_in为气隙磁阻,Rb_in为永磁体磁桥磁阻,Rm为永磁体磁阻,Φr为永磁体磁通,μ0为空气磁导率,Br为永磁体剩磁,Φg为气隙磁通,Φb为磁桥磁通,Bb为磁桥磁密,Sr为转子表面磁通穿过的面积。
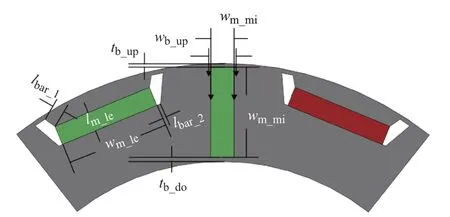
图3 CR-PMSM转子剖面图Fig.3 Profile of CR-PMSM rotor

图4 CR-PMSM等效磁路图Fig.4 Equivalent magnetic circuit diagram of CR-PMSM
磁阻的表达式为
结合图4与磁阻表达式,由磁路法可得气隙、永磁体及磁桥磁通为
式中,RA,RB,RC,RD,RE,RF,RG,RH,rA,rB,rC含义如下所示
综上,可有气隙磁密Bg为
1.2 CR-PMSM轴向磁拉力
采用张力张量法所得转子铁芯表面轴向磁拉力的微分形式为
式中,Bgn为气隙磁密法向分量的均方根值;dS为转子表面磁通穿过的单位等效面积,其表达式为
式中,α为锥角,θ为转子圆周角度。综上可得
式中,z为电机轴向位移。忽略电机轴向长度及转子外圆中间端面平均半径这两个电机固定参数,此时,仅可通过改变电机锥角及气隙磁密,进而改变电机轴向磁拉力,其中气隙磁密直接受交直轴电流的影响。
2 CR-PMSM轴向磁拉力影响因素分析
CR-PMSM 由于结构特殊,空载时转子就会产生轴向磁拉力,由式(24)可知,轴向磁拉力受锥角和交直轴电流的影响。
建立有限元参数化模型如图5 所示,该电机相关参数见表1。
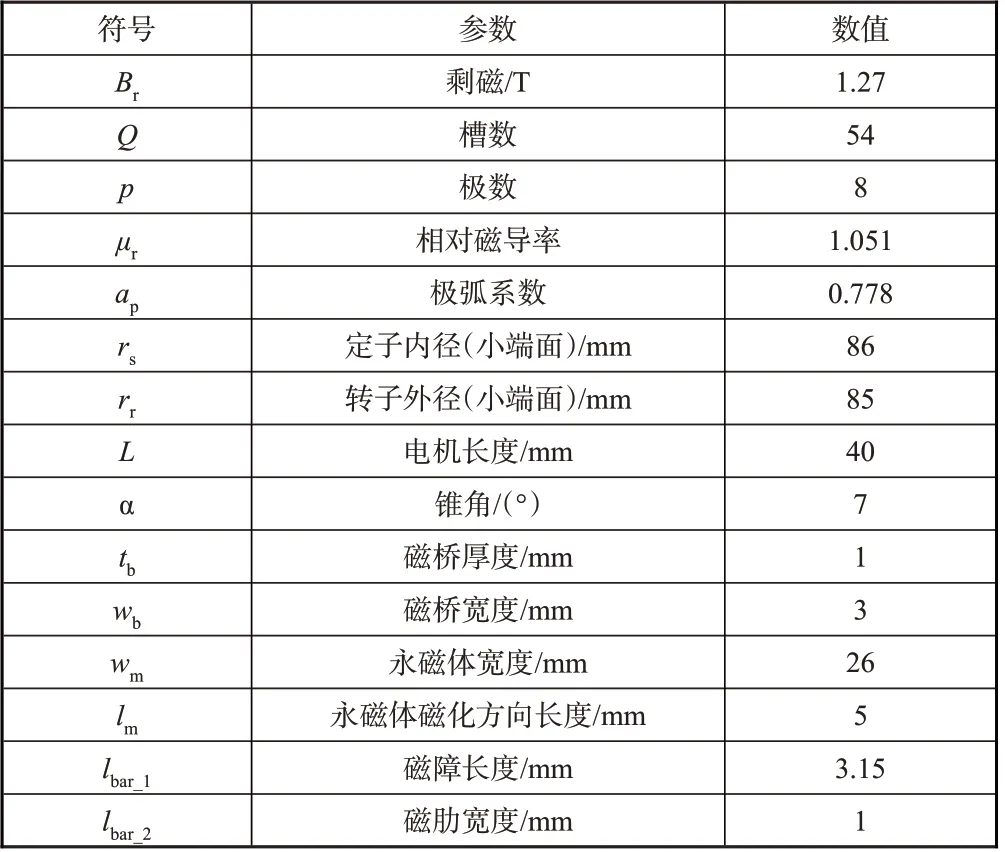
表1 CR-PMSM参数Table 1 Parameters of CR-PMSM
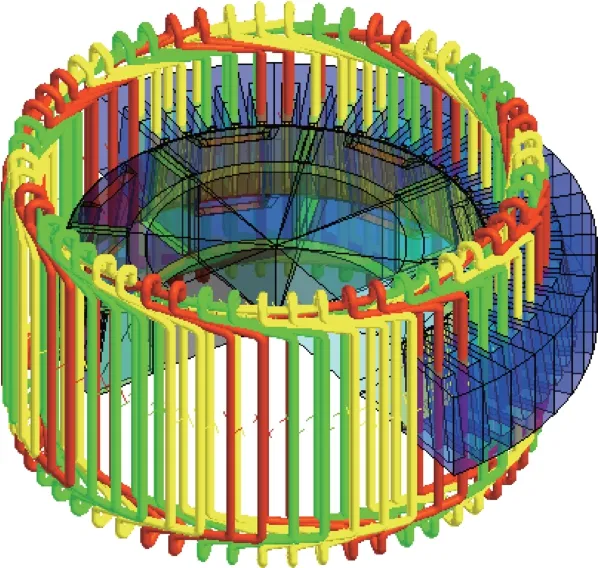
图5 三维有限元模型Fig.5 Three-dimensional finite element model
2.1 锥角对轴向磁拉力的影响
轴向磁拉力在其他参数固定时,随锥角的增大而增大,但考虑电机实际加工时,锥角过大会使电机机械强度变低,并且锥角越大气隙磁密中的谐波含量越大,因此设计时应该避免锥角过大导致的谐波含量过大。电机空载轴向磁拉力与锥角的关系如图6所示。从图6分析可知,电机轴向磁拉力随锥角的增加近似线性增加。对于锥形电推进电机,电机轴承轴向受两个方向相反的力(见图1(b)),分别为螺旋桨轴向力和锥形电机的轴向力。因此,在合理锥角范围内,随着锥角的增加,电机所产生的能够抵消轴承所受轴向外力的能力逐渐增强。

图6 空载轴向磁拉力与锥角关系Fig.6 Diagram of the relationship between no-load axial magnetic force and cone angle
2.2 交直轴电流对轴向磁拉力的影响
从轴向磁拉力的数学模型分析可知,轴向磁拉力直接受气隙磁密的影响,在永磁同步电机中,气隙磁密受交变电流影响不利于分析,因此采用双反应理论将交变电流分解为两个独立可控的励磁Id与转矩Iq电流分量。在不同锥角(cone)下,当直轴电流单独作用时,此时直轴电流对轴向磁拉力的影响如图7所示。
分析可知,轴向磁拉力随直轴增磁电流(Id>0)的增加而增加,随去磁电流(Id<0)的增加而减小。当直轴增磁电流持续增至定转子铁芯饱和时,气隙磁场不再增加。直轴增磁电流对轴向磁拉力的增幅,强于直轴去磁电流对轴向磁拉力减弱的幅度。
如图8所示,当交轴电流单独作用时,轴向磁拉力随交轴电流的增加而增加。由于本文研究的CR-PMSM为电动机,因此只考虑交轴电流为正时的轴向力变化情况,交轴电流的增大对气隙磁场起到了明显的助磁作用,气隙磁密随交轴电流的增加而增加。而通常情况下,转矩随交轴电流增加而增加,相同转速下功率随转矩增加而增加,即随功率增加,锥形电机产生的轴向力增加。同时分析图7、图8 可知,当交直轴电流固定时,电机轴向磁拉力随锥角的增加而增加,符合前文分析。
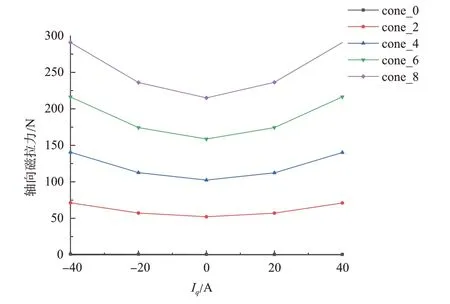
图8 交轴电流单独作用对轴向磁拉力的影响Fig.8 Effect of quadrature axis current on axial magnetic force
交直轴电流单独作用时,在相同的增磁电流下,直轴电流对轴向磁拉力的增幅强于交轴电流对轴向磁拉力的增幅。
当交直轴电流共同作用时,若Id>0,此时Id对轴向磁拉力的增幅占主导地位;若Id<0,此时Iq对轴向磁拉力的增幅占主导地位。当锥角为7°时,调节电机的转速和交直轴电流使电机处于不同功率等级下,此时电机的轴向磁拉力如图9所示。
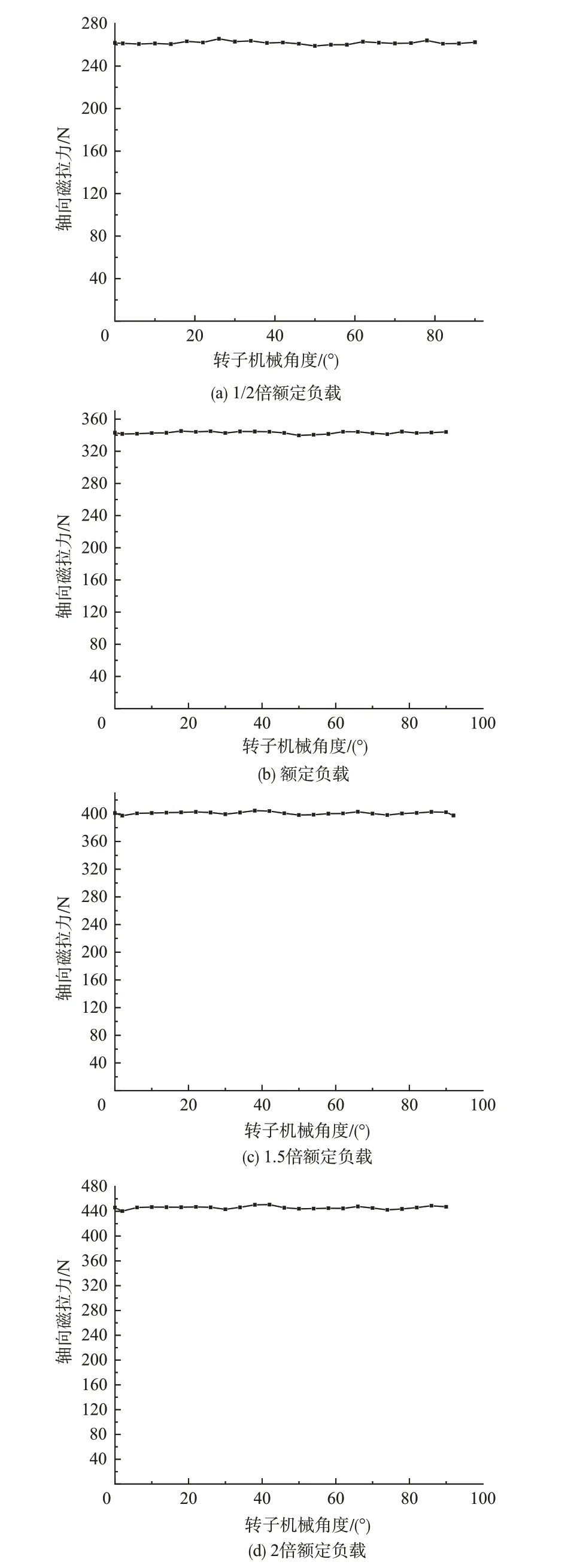
图9 不同功率等级下电机的轴向磁拉力Fig.9 Axial magnetic force of motors at different power levels
进一步研究不同功率下交直轴电流与电机轴向磁拉力的关系,结果见表2。由表2分析可知,随着功率增加,交直轴电流增大,而交直轴电流增大,轴向磁拉力也近似线性增加。为分析不同功率下,锥形电机相对于柱形电机轴承处的降载效果,将不同功率下对应螺旋桨的轴向拉力Fp、电机轴向磁拉力Fz以及轴承处合力Fb=Fz-Fp列于表3。分析表3可知,随着电机功率及交直轴电流的增大,锥形电机轴承的载荷逐渐减小。而对于柱形电机,不同功率下轴承承受的轴向力等于螺旋桨的轴向力。由此可见,同功率等级下锥形电机轴承受力远小于柱形电机轴承受力。

表2 不同功率等级下电机的轴向磁拉力及交直轴电流Table 2 Axial magnetic force and dq-axis currents of motors at different power levels
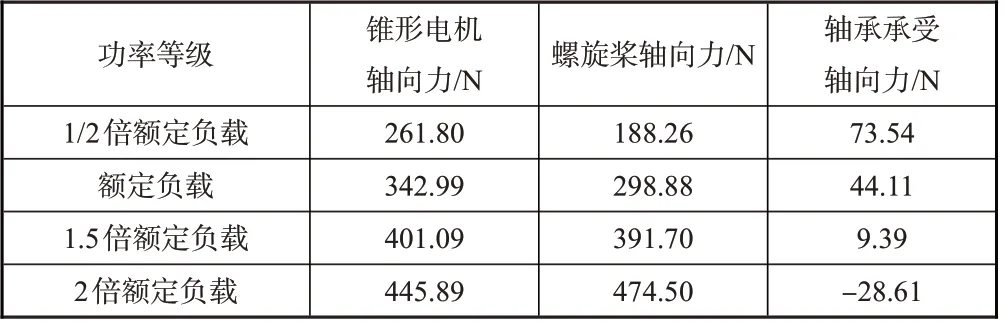
表3 不同功率等级下轴承的合力Table 3 Resultant force at bearings at different power levels
3 结论
本文以电动飞机电推进锥形永磁同步电机为研究对象,利用锥形电机的轴向磁拉力平衡螺旋桨的轴向力,进而降低轴承所受轴向合力,对轴承有保护作用。该研究具有通用性,规律可适用于不同功率等级的电机。具体结论如下:
(1)锥形电机轴向力随锥角增加而增加,即电机所产生的能够抵消轴承所受轴向外力的能力逐渐增强。
(2)直轴电流单独作用时,直轴增磁电流对轴向磁拉力的增幅最强,轴向磁拉力随直轴去磁电流的增加而减小。交轴电流单独作用时,轴向磁拉力随交轴电流的增加而增加。当交直轴电流共同作用时,在Id<0作用区间内,交轴电流对轴向磁拉力的增幅占主导,反之,直轴增磁电流对轴向磁拉力的增幅占主导。
(3)相对于柱形电机,锥形电机自身产生的轴向力,可以有效平衡螺旋桨的轴向力,对电机轴承的降载效果突出。
