中低速磁浮列车走行部迫导向机构转向特性研究

张 硕，李良杰，代瑞珍，王 岩

（1.中车唐山机车车辆有限公司，高级工程师，河北 唐山 063035；2.河北省轨道车辆转向架技术创新中心，高级工程师，河北 唐山 063000）

0 引言

2010年以来，多种形式在中国城市轨道交通领域得到迅猛发展，与此，中低速磁浮列车也实现了从无到有的突破性成就［1］，磁浮列车不同于其他轨道交通车辆，不受传统轮轨关系的限制，具有振动噪声低、运行平稳、曲线通过能力强、爬坡能力强等优点，越来越受到青睐［2-3］。现有运营的磁浮车辆均采用五模块悬浮架结构，为实现前后悬浮架的联动关系从而提高车辆曲线通过能力，故在车体与悬浮架之间设置机械式的迫导向机构，以增加车体的复位能力。但现有的五模块悬浮架在迫导向机构作用下进入曲线时无法完成所有悬浮架实现最佳角度的转向，悬浮架会出现横向滑橇与F 轨接触导致磨损严重、迫导向机构相关部件异常受力的问题，导致磁浮列车的运维成本的增加。

因此，有必要开展中低速磁浮列车走行部迫导向机构转向特性研究。

1 迫导向结构主要组成

由于单节车辆采用五悬浮架结构，因此在每辆车下布置迫导向机构2套，如图1所示，分别布置在第1、2悬浮架和第4、5悬浮架之间，连接端部滑台和中间滑台，纵向对称布置，主要由长T臂、短T臂、T臂支座、T臂连杆以及导向杆等组成。

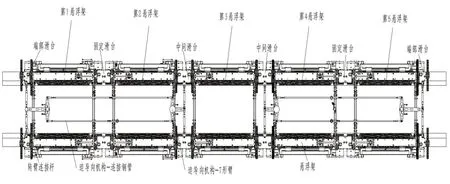
图1 中低速磁浮列车悬浮架走行部俯视图

长T臂和短T臂通过T臂支座安装在车体上，T臂支座中设置有转轴和轴承，使得T 臂可绕垂直与车体地板面的轴线旋转。长T臂和短T臂之间通过T臂连杆连接组成平行四边形机构，由此可使长、短T臂的转角相等，从而在两者之间传递运动关系。T 臂通过四根导向杆与滑台连接，从而可将车体的横向载荷传递到各个横向滑台上，再通过空簧传递到悬浮模块上，迫导向机构组成如图2所示。

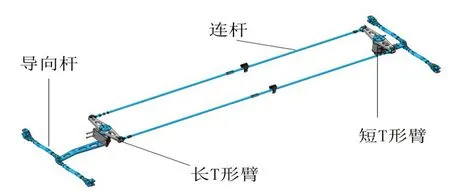
图2 迫导向机构组成

2 理论计算

根据迫导向机构的工作原理，迫导向机构需要通过计算确定的尺寸参数主要包括：长短T 臂尾臂长度比例、导向杆受力、T臂转轴受力。

为进一步分析迫导向机构在清远线运动过程中的运动关系及受力，计算时对迫导向机构、滑台等主要构件进行简化，建立几何参数模型，如图3所示。

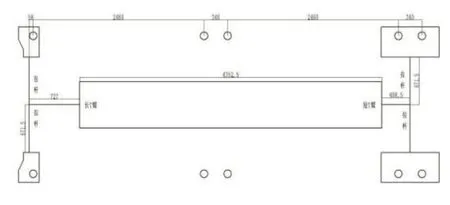
图3 迫导向机构几何模型

2.1 运动学计算

建立如图4所示的直角坐标系。

图4 车辆通过平曲线简图

其中，直线AF表示车体纵向中心线，A、B、C、D、E、F 分别表示1-6 位两侧滑台中心连线中点，曲线表示轨道中心线，a、c、d、f 表示模块在轨道上的投影。由图可知具体参数定义如下：

平曲线半径为R。

由几何关系可得，端部滑台横移量L1：

中间滑台横移量L2：

根据公式计算不同轨道半径下端部滑台和中间滑台横移量如下表1所示。

表1 不同曲线半径对应滑台横向位移

从上表可以看出，不同水平曲线半径下，端部滑台与中间滑台的横向位移均不相同，且位移比也在变化，根据迫导向机构工作原理，这也意味着长短T臂尾臂长度比也应随之变化，才能确保各悬浮模块更好地跟踪轨道曲线，但是实际设计过程中须确定一个固定的长短T臂尾臂长度比。

根据公式（1）和公式（2），当R远大于a和a1时，可以得到

将模块1长度（2688mm）和模块2长度（2800mm）带入公式（3），得到：

根据以上计算，将长短T 臂尾臂长度比设计为1.9，并在后续仿真验证时进行优化。

2.2 受力计算

2.2.1 整车横向受力分析 磁浮车辆匀速在圆曲线半径上运动时，受力主要包括车辆重量、离心力F离、电磁铁产生的悬浮力F悬和导向力F导，受力模型如图5所示。

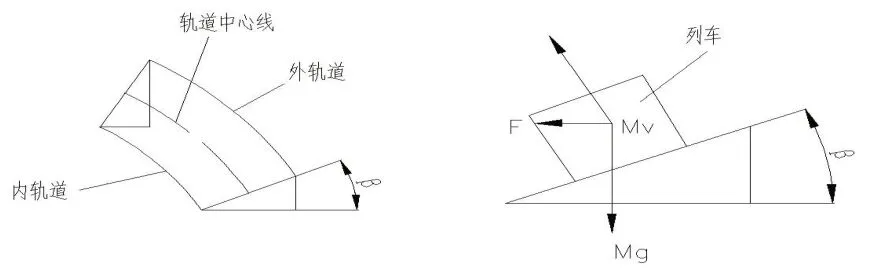
图5 整车弯道受力分析图

根据受力可得：

其中，V—曲线通过速度，M—车辆质量，β—轨道横坡角。

根据清远线线路条件可到：

车场线：半径70m，速度10km/h，无横坡角，车辆为空载工况。

最大超高平曲线：最大横坡角4.63°，车辆为满载工况。

2.2.2 车辆平曲线静浮横向受力分析 由于磁浮车辆导向力传递路径有两条，在静浮状态下，导向力分配关系并不确定，因此在设计时，须考虑导向力分别从两条路径独立传递的极端工况。

根据公式（5）和（6）得到T臂受力：

上述受力将作为迫导向机构设计的载荷条件。

2.2.3 超速进入缓和曲线受力分析 根据清远线线路条件可知，车辆长度15.7m，横坡角变化为0.074°，超速20%通过，平曲线超高150mm。

导向力需求为：

由计算可得，在超速20%通过缓和曲线时，导向力需求相当于重力分量的0.57，没有超过圆曲线静浮工况需要的导向力。

3 仿真计算

根据计算结果，对迫导向机构三维模型进行优化，并将其主要部件进行建模。模型如图6所示。

图6 迫导向机构建模

为提高计算效率，根据清远线线路条件，建立一条包括清远线所有恶劣线路中最恶劣线路的条件，如图7所示。

图7 最恶劣路况复合线路模型

3.1 长短T臂臂长比对转向特性影响

计算时，按照设计车速通过复合路线时各悬浮点横向位移变化情况。T臂臂长比分别选用1.9、1.8、1.7，得到如图8-图10的仿真结果。

图8 不同臂长比下横向位移变化

（1）横向位移变化对比

比较图8（a-c）得知，T 臂比不仅影响连接导向杆的悬浮点的横向位移，也改变了固定滑台对应悬浮点的横向位移，T 臂比为1.8 时，所悬浮点横向位移分布范围相对较小，且更为对称。

（2）受力对比

比较图9和图10得知，T臂比取为理论值1.9时，在圆曲线上导向杆受力减小，说明此时导向杆对应的悬浮点横向偏移减小。同时可以发现T臂比为1.8时，固定滑台导向力更为对称和均匀分布；为1.7时，则会导致固定滑台导向力向负值方向偏移。

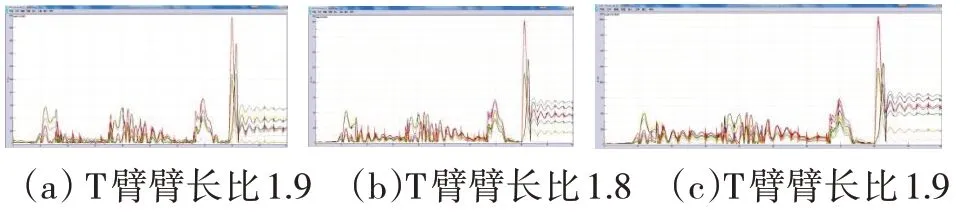
图9 不同臂长比下导向杆受力

图10 不同臂长比下固定滑台受力

3.2 导向杆夹角比对转向架特性影响

导向杆夹角分别设置为161.2°和180°（即滑台导向杆铰点长T臂尾臂导向杆铰点三点共线），计算结果如图11所示。

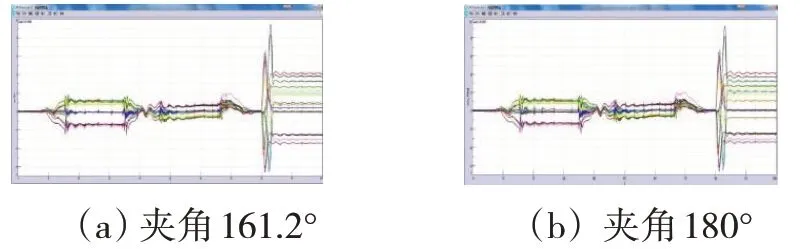
图11 不同导向杆夹角导向杆受力

从上图中可以看出，导向杆尖角并不能减小固定滑台处的电磁铁横移量。考虑到工程化实现的建议性，可以取消导向杆夹角。

3.3 滑台横向位移仿真验证

根据设计速度开展运动学仿真分析，得到如图12的滑台横向位移变化曲线。

图12 滑台横向位移变化曲线

从上图可以看出，滑台在不同半径圆曲线上的横向位移仿真结果与计算结果吻合较好，误差小于3%，能够满足工程设计计算的需要。

4 总结

本文介绍了中低速磁浮列车特有的迫导向机构的组成和工作原理，并对主要参数进行了理论计算，在此基础上开展仿真计算，仿真比较不同迫导向机构设计方案的转向特性，并优化其机构设计。得到以下结论：

根据中低速磁浮列车通过平曲线的工作原理，采用折线拟合圆弧的方式推导得到各滑台横向位移量，并通过运动仿真验证了理论计算的准确性。

推导得到长、短T臂尾臂长度比的计算公式，计算得到T 臂比理论值为1.9，并通过运动学仿真，将T臂比优化为1.8。利用杆系运动的位姿关系，推导得到T臂导向杆夹角理论值为161.2°，并根据仿真计算结果，在清远磁浮旅游专线车辆中取消了夹角，优化后的迫导向机构已经装车并通过试验验证，转向性能优异。