应用不同深度学习代理模型的灯笼型扰流柱通道换热性能分布预测方法比较

2024-02-20高尚鸿张韦馨杨克峰汪翔宇丰镇平

西安交通大学学报 2024年2期

高尚鸿,张韦馨,杨克峰,汪翔宇,丰镇平

(西安交通大学能源与动力工程学院,710049,西安)

近年来,随着现代燃气轮机透平入口温度不断升高,当前透平进口总温已经远高于叶片基体材料的耐温极限[1],不仅对叶片冷却结构设计提出更加苛刻的要求,而且冷却单元设计周期更长、成本更高。透平叶片尾缘和双层壁中常采用扰流柱所组成的阵列,这是因为扰流柱非常有利于提高透平叶片内部冷却空气的湍流度,增强叶片金属部分与冷却空气的对流换热强度,进而降低叶片热负荷。同时,多排扰流柱还能起到支撑作用,增强叶片强度。目前,国内外学者已经对扰流柱阵列分布[2]、扰流柱对劈缝气膜冷效的影响[3]、扰流柱通道内的涡系结构[4]、空气/汽雾工质[5]和扰流柱对双层壁换热特性的影响[6]等进行了广泛和深入的研究。

随着燃气轮机数字化和优化设计水平的提高,为降低实验和计算成本,研究者们提出了基于数据驱动的代理模型方法。基于数据驱动的代理模型是以数据为基础,以数理统计和机器学习等技术为手段,通过建立复杂的函数映射关系来计算预测值的方法[7],是一种包含数据空间采样和预测方法的综合建模技术[8]。传统的代理模型基于统计学理论和机器学习方法来构建预测模型,如多项式响应面模型[9]、径向基神经网络模型[10]、Kriging模型[11]和人工神经网络[12]等。

对传统代理模型,本研究团队(TurboAero团队)开展了相关研究工作。刘战胜等[13-15]分别用径向基函数模型和Kriging模型对透平叶型、端壁和气膜孔进行优化;张韦馨等[16]利用径向基神经网络代理模型和杜鹃搜索优化算法对平板气膜孔进行了优化。但是,目前的传统数学统计和机器学习方法过多依赖于人工特征提取,而深度学习可自适应地逐层挖掘特征,更适于高维、海量和非线性问题。

随着深度学习技术的发展与成熟,生成对抗网络(generative adversarial networks,GAN)[17]已经被国内外不少学者应用到燃气轮机透平叶片的冷却性能预测和优化设计当中。Yang等[18]研究了基于生成对抗网络的发散冷却效率分布预测;戴维等[19]研究了基于生成对抗网络的透平端壁气膜冷却建模方法;李左飙等[20-21]研究了生成对抗网络对气膜冷效的预测;Jiang等[22]研究了多尺度pix2pix网络对透平叶片前缘气膜冷效的预测。

综上所述,目前尚未有相关文献系统比较深度学习代理模型和传统代理模型在扰流柱通道端壁面换热分布预测方面的优劣。因此,本文针对本研究团队杨克峰等提出的灯笼型扰流柱通道结构[23],经过拉丁超立方抽样得到7个不同训练数据集,构建了多项式响应面模型(RSM)、径向基函数模型(RBF)、径向基神经网络模型(RBFNN)、Kriging模型、总体平均近似模型(Ensemble)[24]、有/无残差网络模块的pix2pix模型[25]、pix2pixHD模型[26]、CycleGAN模型[27]和StarGAN模型[28]。最后,从预测精度、计算成本和泛化能力3个方面系统评估了各代理模型对灯笼型扰流柱端壁面换热性能分布的预测能力。

1 数据集及评价指标

1.1 数据集及数据处理

灯笼型扰流柱通道模型的几何特征如图1所示,共包含8排扰流柱,扰流柱根部直径D为25.4 mm。

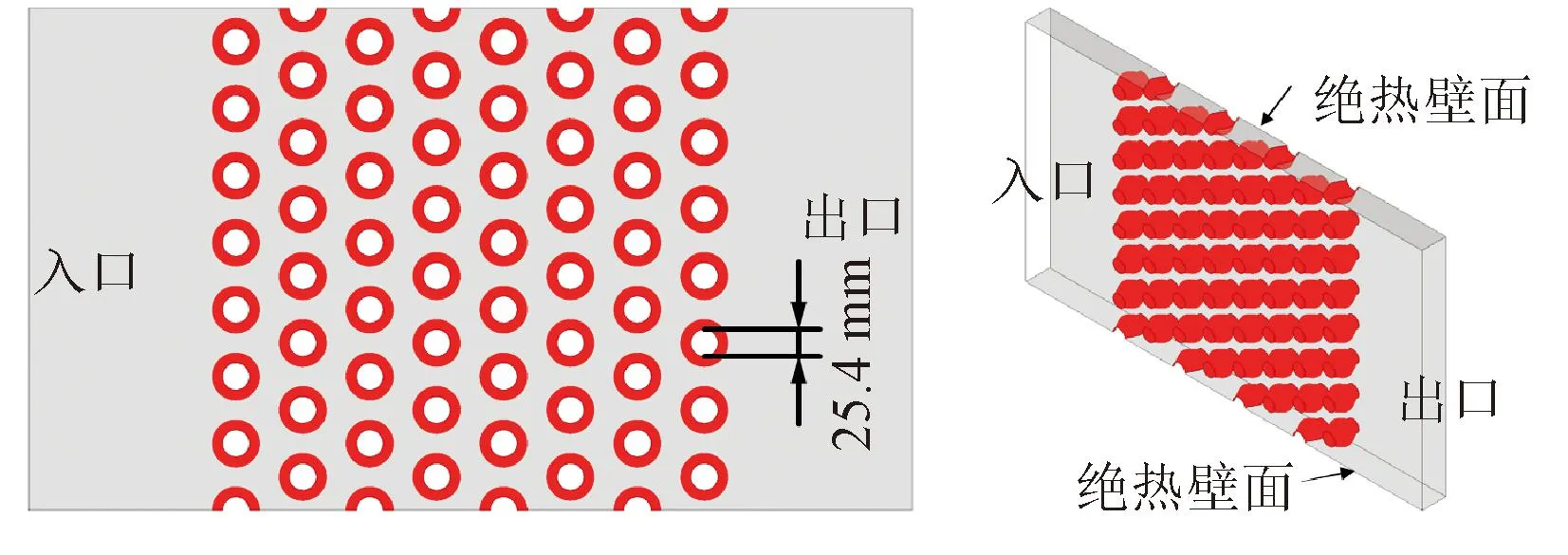
图1 扰流柱通道几何示意Fig.1 The geometry of lantern-shaped pin-fin channel

灯笼型扰流柱的原型是圆柱与球体的合并,圆柱和球体同心,球体直径为1.7D。灯笼型扰流柱的截面采用B样条曲线旋转而成,B样条曲线由9个数据点插值而成,包括4个固定数据点和5个可变数据点,数据点对称分布,因此只选择其中3个可变数据点为截面参数,如图2所示。截面参数均沿扰流柱径向平移一段距离作为变量空间,3个截面参数的变化范围为0.1D。具体地:z1～z3的变化范围分别为-2.54～0、-1.27～1.27、-1.27～1.27 mm;负号方向表示沿径向向扰流柱外侧移动,正号方向表示沿径向向扰流柱内侧移动。

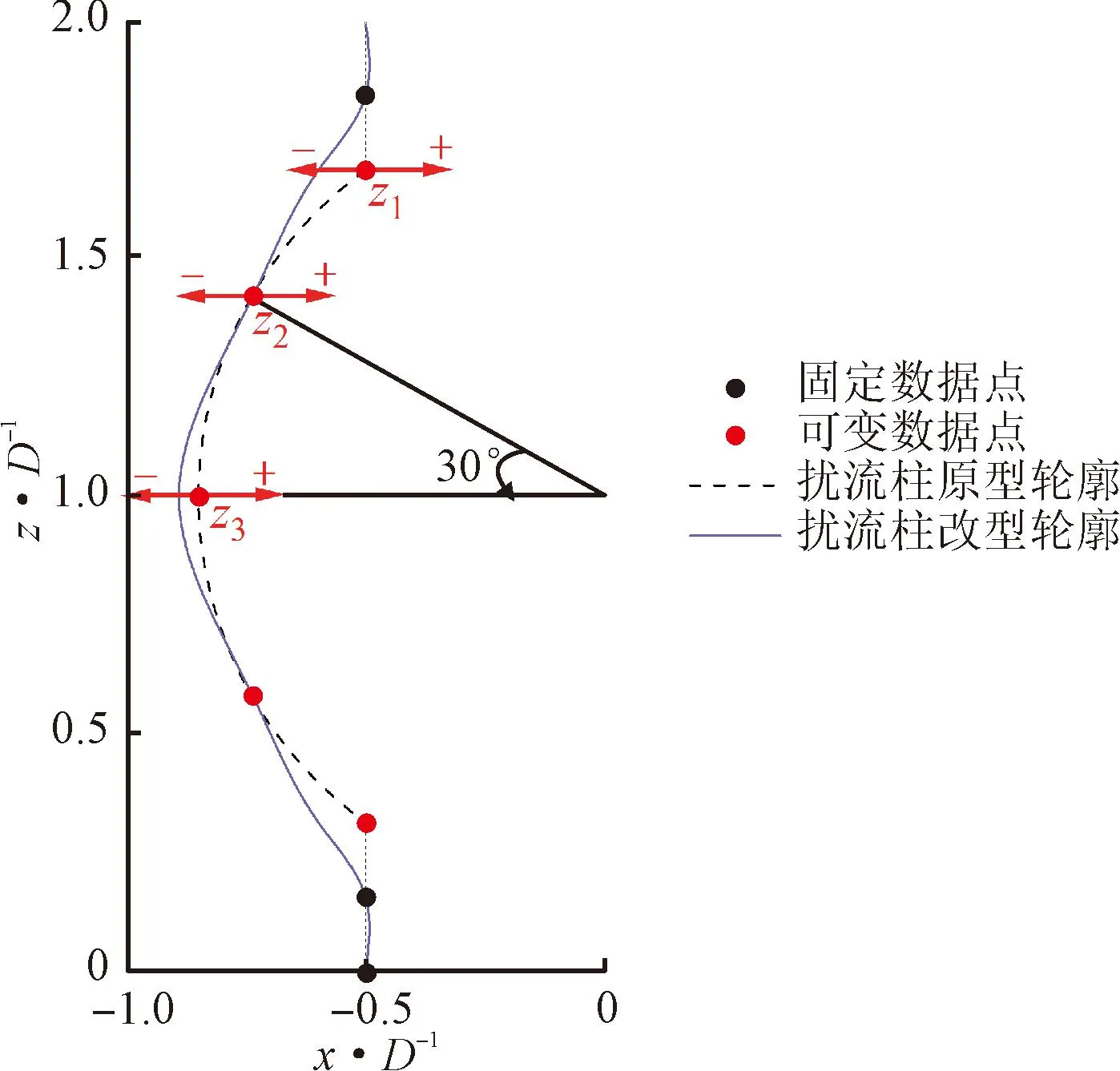
图2 扰流柱截面轮廓示意Fig.2 The geometry of lantern-shaped pin-fin cross section

详细的物理边界条件和CFD数值计算过程可参考文献[23]。本文通过拉丁超立方抽样得到50个训练样本参数和10个测试样本,为了比较代理模型在不同训练样本数下的泛化能力,又通过拉丁超立方抽样分别得到样本数为25、12、6和3的数据集。为进一步研究代理模型对不同数据特征的泛化能力,本文还根据换热云图展向分布特点,将所有样本分为两份:24个宽样本和26个窄样本,如图3所示。宽样本表示扰流柱后一段区域展向换热较强,表现为白色区域宽短。窄样本表示流向换热较强,表现为白色区域细长。

图3 宽样本和窄样本的特点Fig.3 Features of wide and narrow samples

在数据处理模块中对所有数据进行归一化和灰度化,并插值为长宽均为256的方形矩阵,深度学习模型的数据处理流程如图4所示。在计算设备上,传统代理模型采用6核i5-9400F CPU计算,深度学习代理模型采用一颗12 GB显存的NVIDIA GeForce RTX 2060独显计算。

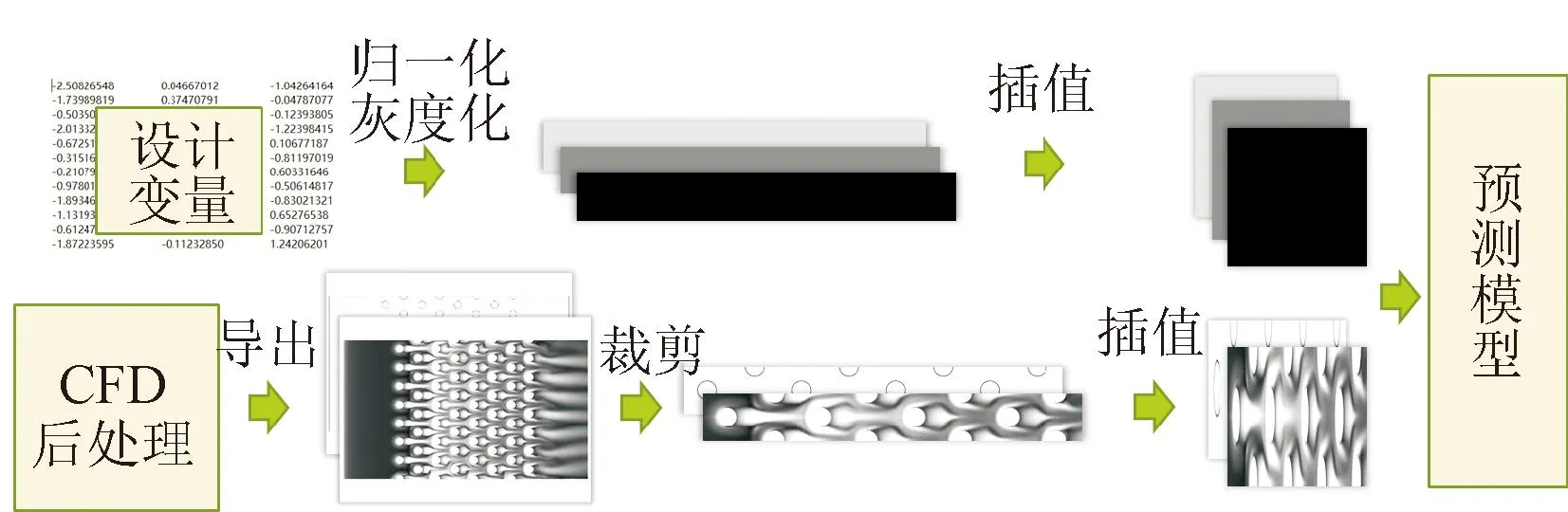
图4 深度学习代理模型的数据预处理流程Fig.4 Data preprocessing flow for deep learning

本文共有10个测试样本,但由于篇幅有限,本文仅展示5个测试样本的预测结果分布,从上到下依次按Test 1～Test 5排列,各个样本的截面参数如表1中所示。

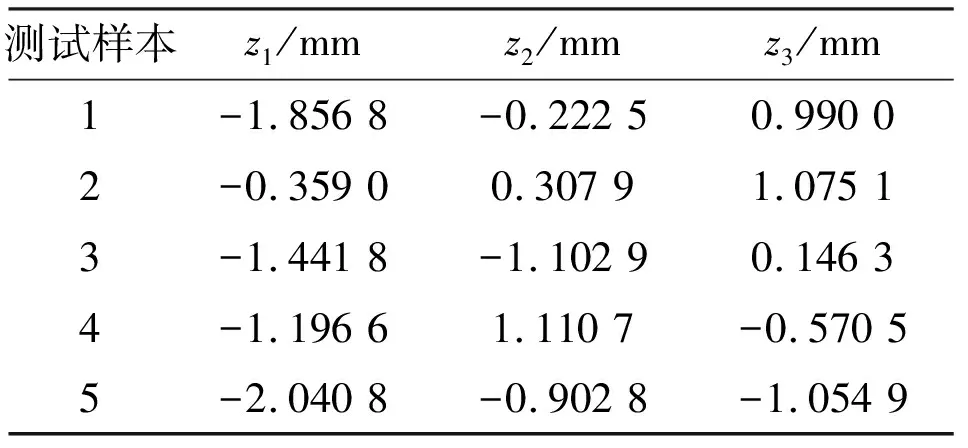
表1 5个测试样本的截面参数

1.2 预测精度的评价指标

本文在CFD后处理过程中采用Nu来表示换热性能,计算公式为

(1)

式中:h为换热系数;Dc为通道的水力直径;λ为流体热导率。本文基于Nu云图进行数据处理,预测云图中的Nu的范围为0～200。

为了评估真实云图和预测云图之间的差异,本文对云图中的像素值进行简单处理,公式为

(2)

式中:y为真实云图每个像素点的评估值;p为像素灰度,取值范围为0～255;Nu的上限为200。

本文将代理模型的预测精度指标分为面平均值的预测精度和分布的预测精度。面平均值的精度用相对误差来衡量,公式为

(3)

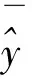
换热分布的预测精度用云图上所有点的平均相对误差来衡量,公式为

(4)

式中:q为云图上的像素点数。

均方误差也可以衡量Nu分布预测精度,本文统一对所有点进行归一化后计算其均方误差,公式为

(5)

2 深度学习代理模型介绍及构建

2.1 有/无残差网络的pix2pix模型

基于生成对抗网络的pix2pix模型可以方便实现图-图翻译和多域转换。pix2pix模型包括生成器、判别器和识别器3个神经网络,其生成器为U-Net结构[29],将几何轮廓图作为条件输入生成器,即可输出对应图像。图5为本文所用的pix2pix网络结构,z为扰流柱的截面参数,z′为预测值。

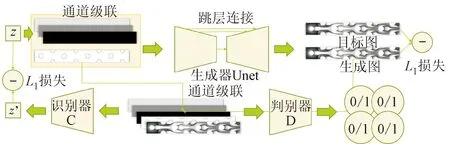
图5 pix2pix网络结构Fig.5 Network structure of pix2pix

本文的生成器主要有两种,一种采用普通卷积层,另一种采用残差网络。图6展示了本文采用的残差神经网络单元(residual network,ResNet)[30],其由I个普通卷积层组成,输入数据通过卷积层后再与输入相加。

图6 残差网络结构Fig.6 Residual network structure

判别器的作用是判断生成器输出结果的真假。识别器的作用是通过云图识别其对应的截面形状参数,保证生成结果的多样性。其结构的前半部分与判别器基本相同,后半部分采用全连接层。

pix2pix的损失函数由生成器和判别器的对抗损失、预测云图和目标云图的L1损失以及预测截面形状参数和目标截面形状参数的L1损失构成。

2.2 pix2pixHD模型

本文所用的pix2pixHD网络结构如图7所示。图中,z′和z″为不同的预测值。在残差pix2pix基础上更改U-Net生成器为多尺度的U-Net生成器,并增加了多尺度判别器和识别器。其判别器和识别器的结构均与残差pix2pix相同,损失函数也相同。由于显存受限,本文仅在残差pix2pix模型基础上增加一个小尺度网络。

图7 pix2pixHD网络结构Fig.7 Network structure of pix2pixHD

2.3 CycleGAN模型

本文所用的CycleGAN模型的基本组成结构如图8所示,包含A、B两个生成器,实现了输入和输出的互相转换。循环一致损失为图中黑色箭头标注的过程,生成器B生成的几何特征经过生成器A生成对应的云图(即循环输出),并与目标云图计算L1损失。同理,生成器A生成的云图也要经过生成器B生成对应的几何特征(即循环输入),并与目标的输入参数计算L1损失。

2.4 StarGAN模型

本文所用的StarGAN仅用来实现几何特征到云图的映射部分,通过两个编码器对输入参数进行进一步编码再输入生成器进行预测,整个网络的结构如图9所示。两个编码器共同对几何参数提取特征,进一步提高了深度学习的特征提取能力。

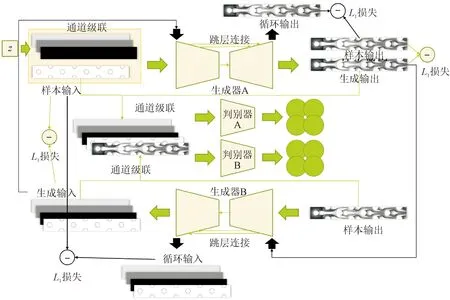
图8 CycleGAN网络结构Fig.8 Network structure of CycleGAN

图9 StarGAN网络结构Fig.9 Network structure of StarGAN

3 不同模型预测能力的对比分析

3.1 训练样本数为50时的预测性能对比

3.1.1 整体的预测能力对比

表2 各代理模型评价指标的样本平均值

3.1.2 细节的预测能力对比

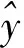
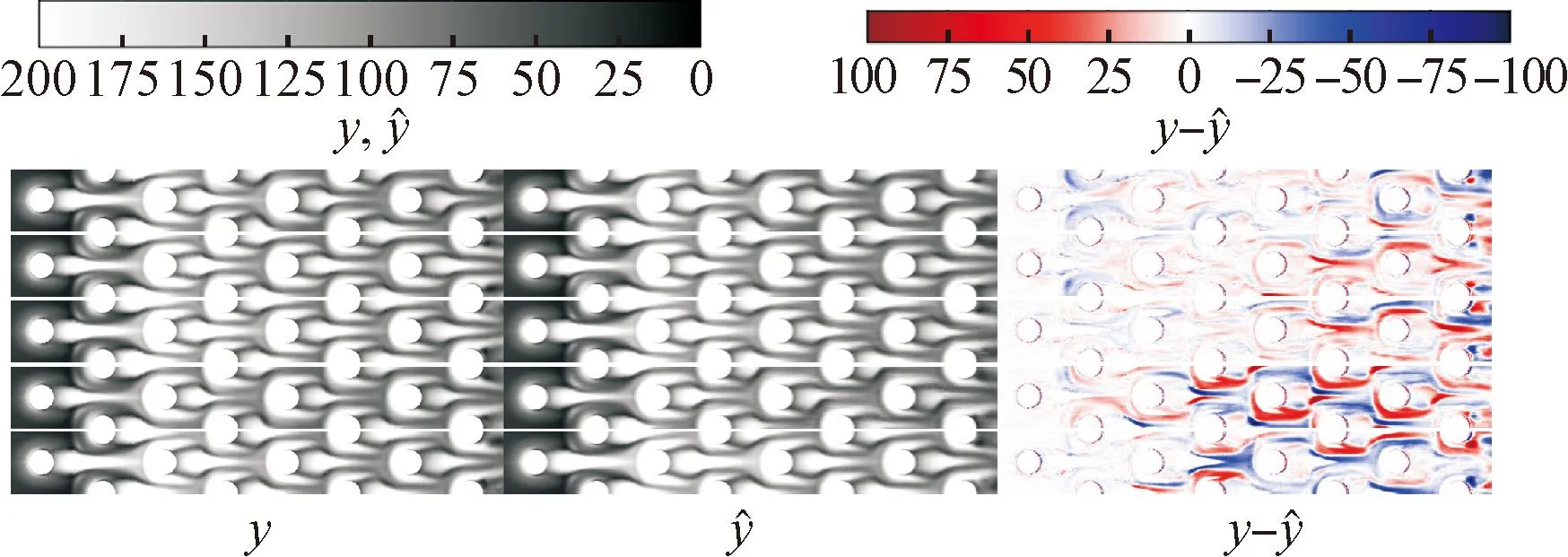
(a)无残差pix2pix

(b)残差pix2pix

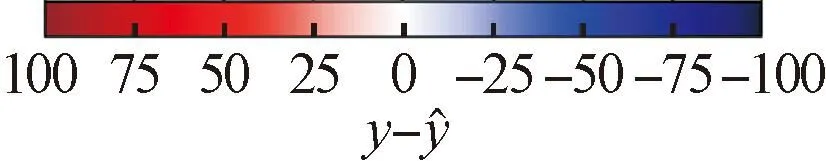
(a)pix2pixHD

(b)CycleGAN

(c)StarGAN

(d)RSM

(e)RBF

(f)RBFNN

(g)Kriging

(h)Ensemble

同一代理模型对不同测试样本的预测精度也不相同。例如,深度学习代理模型对测试样本4、5的预测误差较大,但RSM模型仅对测试样本1误差较大,在其他测试样本上预测效果好。这对代理模型的整体预测能力有直接影响。

此外,在扰流柱边缘区域,深度学习模型预测误差较大,这是由于图像缩放导致数据失真。

3.1.3 时间成本对比

表3展示了各代理模型的建模时间和预测时间。从时间成本来看,传统代理模型的建模时间可忽略,但是深度学习代理模型的训练时间成本较高。无残差pix2pix模型训练时间最少,训练仅耗时2.08 h;由于残差网络及训练参数的增加,其他深度学习代理模型训练时间也逐渐增加,StarGAN训练时间甚至可达34.2 h。代理模型的预测时间均非常短,主要的时间成本在于模型的构建和训练阶段。

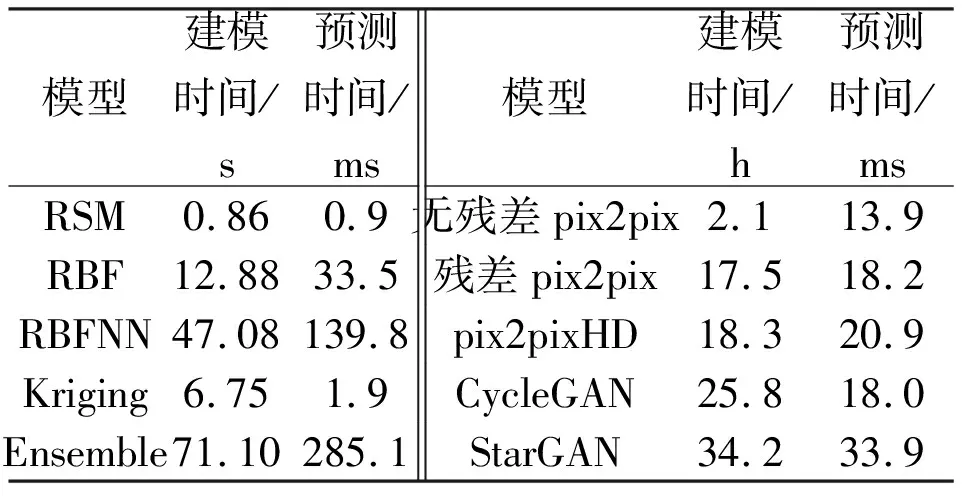
表3 各代理模型的时间成本

3.2 训练样本数为50时的流向和展向Nu分布

图12 流向和展向位置标记Fig.12 Flow direction and span direction position

图12为展向和流向的位置标记,流向距离总长记为L,展向距离标记为S。本小节以测试样本1和测试样本4为例,进一步分析各代理模型对局部细节的预测能力。

3.2.1 测试样本1的预测能力对比

如图13所示,在换热云图的流向分布上,深度学习代理模型预测结果基本一致,因此仅展示了有/无残差网络的pix2pix模型的对比。对前两排扰流柱,传统代理模型基本与真实值一致;对后6排扰流柱,深度学习代理模型对波峰和波谷的预测精度更高。

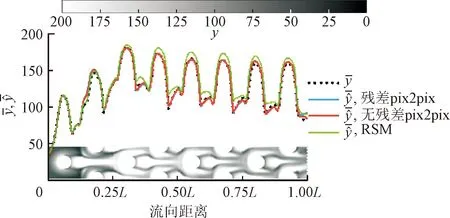
(a)无残差pix2pix与RSM

(b)RBF与Kriging

展向分布如图14所示,各残差网络模型之间相差不大,无残差pix2pix模型在0.75S～S之间比残差pix2pix模型更接近真实值。传统代理模型无法准确预测波峰波谷的位置,其预测误差远远大于残差pix2pix模型。测试样本1的展向分布真实值基本呈现对称分布,深度学习代理模型与RSM模型的预测结果基本符合对称分布的规律,但其他传统代理模型预测规律并不对称。

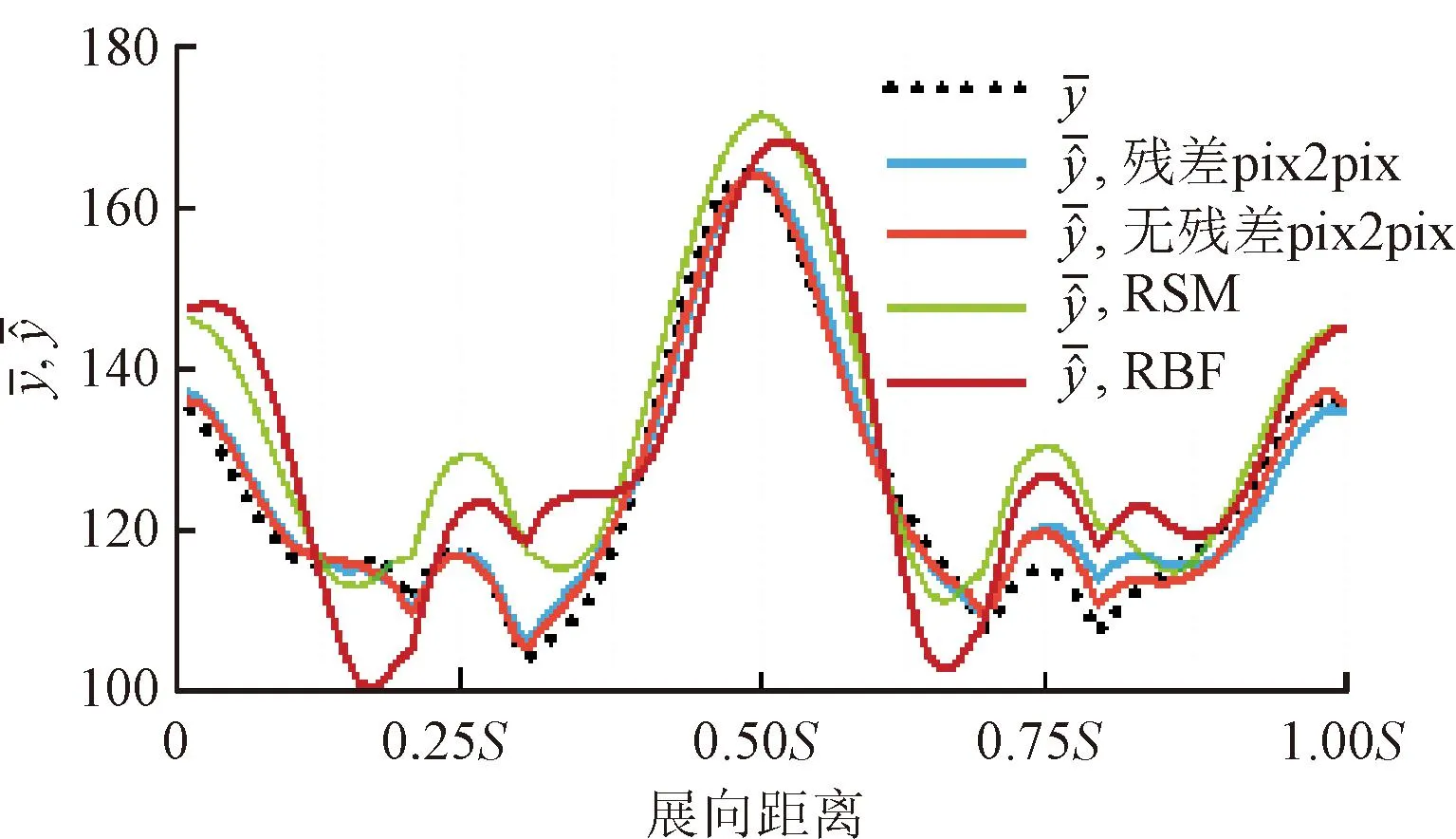
(a)无残差pix2pix、RSM与RBF

(b)RBFNN、Kriging与Ensemble

3.2.2 对测试样本4的预测能力对比

从流向分布来看,测试样本4的预测中,各个代理模型的预测结果与真实值基本一致,如图15所示。

图15 各个代理模型的流向分布的对比(样本4) Fig.15 Comparison of flow direction distribution between different models (sample 4)

图16展示了各个代理模型的展向分布。可见各代理模型预测精度均不好,尤其是在0.25S～0.375S和0.75S～0.875S两个区间,预测结果均远远低于真实值。残差pix2pix模型预测精度略高于无残差pix2pix模型;传统代理模型之间的区别较为明显,RSM模型的预测结果与真实值较为接近,也优于残差pix2pix模型。整体上,测试样本4的展向分布依然呈对称分布,但是只有RSM模型的预测结果符合对称规律,其他代理模型的预测规律较为相似,但均不是对称分布。

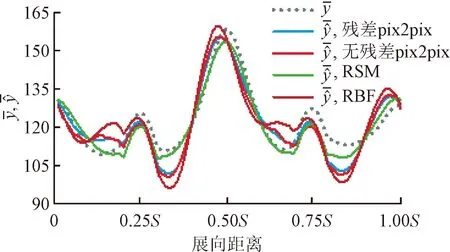
(a)无残差pix2pix、RSM与RBF

(b)RBFNN、Kriging与Ensemble

3.3 泛化能力对比分析

3.3.1 训练样本数对预测精度的影响

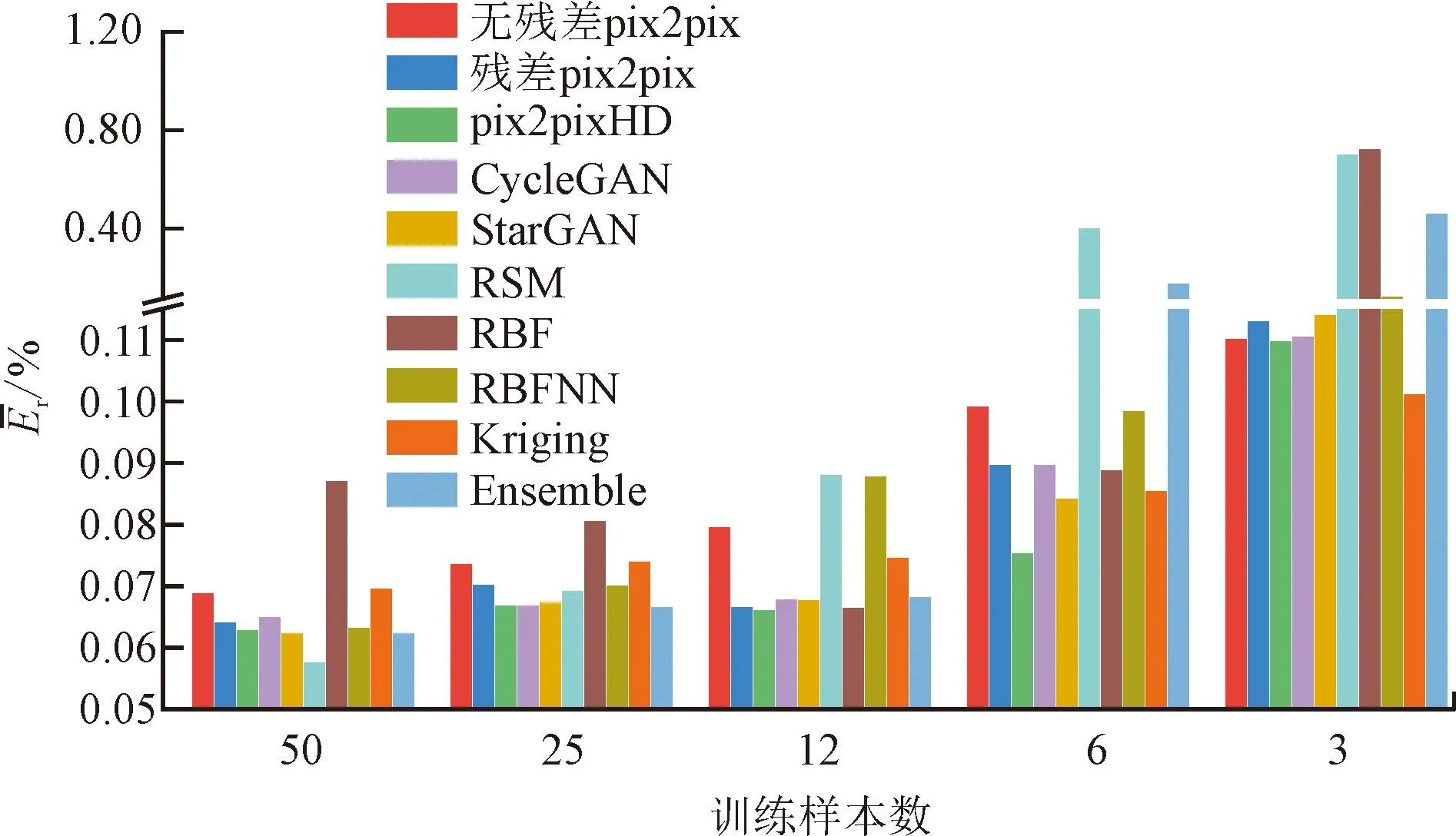
图17 不同样本数曲线 curves for different sample sizes

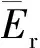
在不同训练样本数条件下,各个代理模型的预测能力会发生非常明显的变化。例如,当训练样本数从50减少为25时,RSM模型误差大幅增加,在预测精度上失去优势;当训练样本数从50减少到12时,RBF模型误差降到最低值,明显优于其他代理模型。但是,有残差网络的深度学习模型的预测误差一直保持在较低水平。

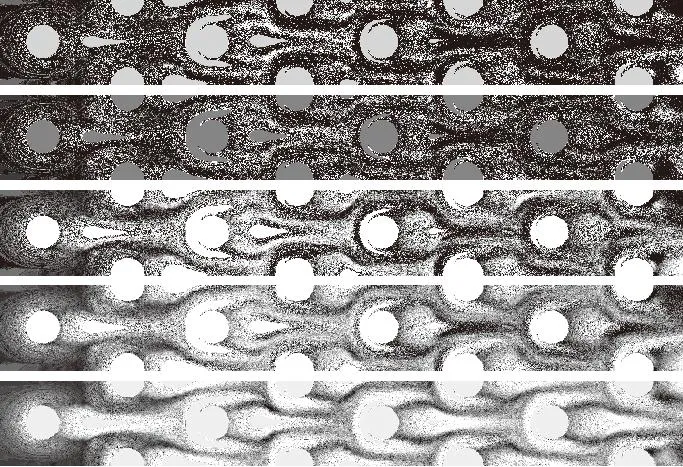
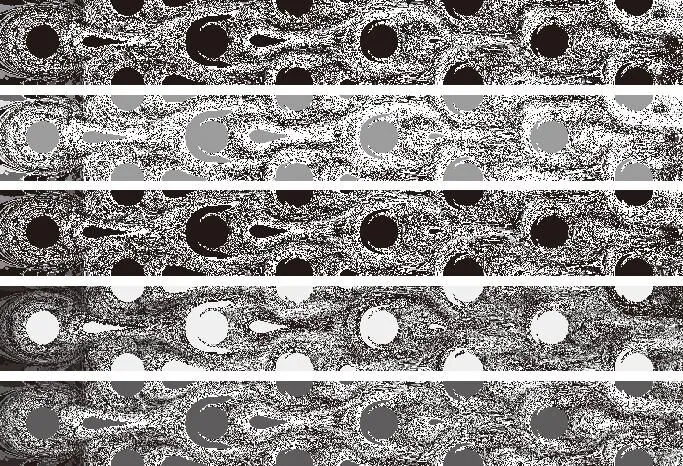
图18和图19以残差pix2pix模型和RSM模型为例,展示了不同的训练数据集情况下的换热分布云图,训练集样本情况详见1.1小节。可以看出:残差pix2pix模型随样本数减小,预测结果没有突兀的变化,但是当预测样本数为3时,其预测结果几乎已经变为3种固定分布,出现过拟合现象;RSM模型在样本数为减小到25时,已经有局部区域出现

(a)真实分布

(b)50

(d)12

(e)6

(f)3

(g)宽样本

重影,并随样本数减小逐渐明显,当样本数为6时,预测结果严重失真。

(a)真实分布

(b)50

(d)12

(e)6

(f)3

(g)宽样本

(h)窄样本

图20展示了训练样本数为3时,其他传统代理模型的换热分布预测结果。可以看出,Kriging模型和RBFNN特征学习能力弱,所有测试样本的预测结果均趋于一致,类似于机器学习领域的模式崩溃现象;RBF模型和Ensemble模型有严重的失真现象,可见Ensemble的加权平均思想容易受子模型的干扰。因此,在样本数较少时:深度学习代理模型预测精度和泛化能力均较强;Kriging模型和RBFNN模型虽然泛化能力强,但预测结果趋同;RSM、RBF和Ensemble模型严重失真。

(a)RBF (b)RBFNN(c)Kriging (d)Ensemble

3.3.2 训练样本特征对预测精度的影响

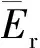
图21 样本特征变化对预测精度的影响Fig.21 The effect of sample features on prediction accuracy

4 结论

本文针对灯笼型扰流柱阵列通道,以扰流柱面上的3个点位置为设计变量,通过拉丁超立方抽样形成了不同的训练数据集和测试数据集,基于数据驱动思想,构建了RSM、RBF、RBFNN、Kriging、Ensemble等5种传统代理模型和无残差pix2pix、残差pix2pix,pix2pixHD、CycleGAN和StarGAN等5种深度学习模型,以预测精度、计算成本和泛化能力为预测能力的评价指标,详细分析了各代理模型在全局整体预测和局部细节预测方面的优势与不足,得到的主要结论如下。

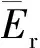
(2)当训练样本数为50时,RSM模型的预测能力较高,有残差网络的深度学习代理模型次之,RBF模型预测能力较差。

(3)从局部细节来看,不同测试样本上各代理模型表现不同,对于测试样本1,深度学习代理模型预测能力最高,对于测试样本4,RSM模型预测效果最好。对于扰流柱边缘,深度学习代理模型存在一定误差,仍需要对数据处理方法进行改进。