双馈式抽水蓄能机组功率调节参数的敏感性分析
2024-02-18孙茂祥王利英王大开樊红刚张佳杰王泽阳
孙茂祥 王利英 王大开 樊红刚 张佳杰 王泽阳


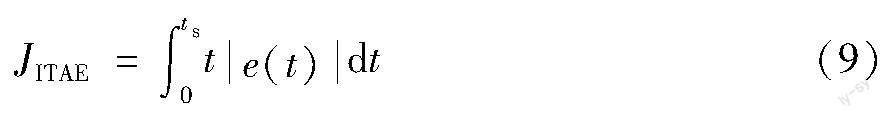
摘要:為了研究双馈式抽水蓄能机组功率调节控制器参数对系统控制性能的影响,基于功率调节控制策略,采用正交试验设计方法分析功率调节控制器参数的敏感性。针对功率调节控制器中的4个参数(每个参数分别选取4个水平)进行正交设计,选取ITAE作为优化目标,筛选出稳定工况,通过极差分析,量化参数的敏感程度,区分出对系统控制性能产生影响的主要参数和次要参数。计算结果表明,较小的ITAE指标值代表系统动态响应品质高,误差更小且收敛速度更快。电流调节模块的比例系数对系统控制性能影响较大,而功率调节模块的积分系数、电流调节模块的积分系数功以及电流调节模块的比例系数对系统控制性能影响较小。功率调节控制器参数的敏感性分析,为双馈式抽水蓄能机组在电力系统中的可靠运行提供了理论依据。
关键词:双馈式抽水蓄能机组;功率调节;正交试验设计方法;控制器参数;敏感性
中图分类号:TV734 文献标识码:A 文章编号:1001.9235(2024)01.0131.09
Sensitivity Analysis of Power Regulation Parameters for Doubly.Fed Pumped Storage Units
SUN Maoxiang1,WANG Liying1,WANG Dakai1,FAN Honggang2*,ZHANG Jiajie3,WANG Zeyang1
(1.School of Water Conservancy and Hydroelectric Power,Hebei University of Engineering,Handan 056038,China;
2.Department of Energy and Power Engineering,Tsinghua University,Beijing 100084,China;
3.College of Civil Engineering,Hefei University of Technology,Hefei 230000,China)
Abstract: This paper aims to investigate the impact of power regulation controller parameters on the system's control performance of doubly.fed pumped storage units.Based on the power regulation control strategy,the paper employs an orthogonal experimental design to analyze the sensitivity of power regulation controller parameters.Four parameters in the power regulation controller (each parameter selected at 4 different levels) are subjected to orthogonal design.Integral of time.weighted absolute error (ITAE) is chosen as the optimization objective.Stable operating conditions are identified through range analysis.The sensitivity of parameters is quantified by range analysis to distinguish the major and minor parameters affecting the control performance of the system.The computational results demonstrate that a smaller ITAE value indicates higher dynamic response quality of the system,smaller errors,and faster convergence speed.The proportional coefficient of the current regulation module significantly influences the control performance of the system.However,the integral coefficient of the power regulation module,the integral coefficient of the current regulation module,and the proportional coefficient of the current regulation module have a relatively minor effect.The sensitivity analysis of power regulation controller parameters provides a theoretical foundation for the reliable operation of doubly.fed pumped storage units in the power system.
Keywords:doubly.fed pumped storage unit;power regulation;orthogonal experimental design method;controller parameters;sensitivity
在过去十年中,可再生能源主导系统中的储能变得越来越重要[1],抽水蓄能电站是一种重要的储存能源的形式,双馈式抽水蓄能机组在电力系统中应用越来越广泛。
胡万丰等[2]研究了双馈式抽蓄机组负荷小扰动时功率调节过程动态特性。龚国仙等[3]提出了一种双馈式抽水蓄能机组控制策略,使机组在负载较轻的情况下实现满载调速。谢宁宁[4]建立交流励磁抽蓄机组优化模型,提出功率阶跃变化和斜坡变化的分段最优功率协同控制策略。Schmidt等[5]推导了变速抽水蓄能电站的综合模型,在优化问题中系统地考虑了操作约束,且针对不同工况计算最佳操作点。Alizadeh等[6]评估比较了定速和变速抽水蓄能电站性能,并给出了基于DFIM和基于同步机的抽水蓄能电站的数值模型。Sarasúa等[7]研究了具有长管道系统的双馈式可变速抽蓄机组的动态响应,并提出了2种机组调节准则。
正交试验是典型的多因素多层次分析方法,可以直觀地描述整个设计空间的情况并进行测试。徐超等[8]利用正交试验研究了相应模型参数对围护结构变形的影响。叶建和等[9]用改进正交试验法对某电站调速器参数进行了优化,优化后的调节系统性能曲线得到很大改善。罗敏等[10]基于正交优化设计法,在某水电站的水轮机调速系统中通过仿真实现了PID调节器参数的精细整定,显著提升了系统性能。金波等[11]提出一种基于正交试验的程序化方法,并在理论上证明了其收敛性,为参数优化提供了更稳定的框架。
彭安华等[12]采用正交试验法优化了PID控制器参数,使得机床闭环伺服系统的超调量大幅度降低。李路[13]通过正交数值进行仿真试验,根据极差分析结果和层次分析法确定了影响隧洞顶部竖向位移主次因素。
目前国内外学者对双馈式抽水蓄能机组双馈电机的建模与相应控制策略以及功率调节进行了较多的研究,但是对于功率调节中的参数研究相对较少。考虑到正交试验的优点,采用正交试验设计方法对功率调节控制器参数进行敏感性分析[14],区分出影响计算结果的主要参数和次要参数,进而研究如何选取合适的功率调节控制器参数来改善系统的控制性能。
1 双馈式抽水蓄能机组
1.1 双馈式感应电机模型
双馈式抽水蓄能机组结构见图 1[2], 该电站包括水力系统和电力系统。水力系统由上下水库、引水管道、调压井和水泵水轮机等组成。电力系统包括双馈感应电机和AC/DC/AC变流器等。
在抽水蓄能机组过渡过程中采用特征线法求解管道瞬变流,采用Suter法描述水泵水轮机机组特性,用机组转速平衡方程和力矩平衡方程求解,调速器采用PID调节器对导叶开度进行控制。
在理想的双馈感应电机(Doubly.Fed Induction Machine,DFIM)模型[15]中,DFIM可以被看作定子和转子上的三相绕组。在以同步速度ωs旋转的dq坐标系下,DFIM的电压方程和磁链方程为:
式中 u——电压,V;i——电流,A;ψ——磁链,Wb;ω——电角速度,rad/s;R——电阻,Ω;L——电感,H;Lm——激磁电感;r——转子变量;s——定子变量; d——直轴分量;q——交轴分量;ωm——转轴电角速度。
定子和转子绕组电角速度之间存在关系:
ωs=ωm+ωr(3)
电机与水泵水轮机通过转轴机械相连,J为转动惯量(kg·m2),T为力矩(N·m)满足以下机械方程:
通过该方程,电机与水泵水轮机实现了耦合。式中Tload——水力矩;p——电机磁极对数。
而电磁力矩Tem可由式(4)求得:
其中,Im代表取空间矢量虚部,上标*代表空间矢量的共轭。
定子和转子有功功率P(W)和无功功率Q(Var)为:
1.2 机组功率调节过程控制策略
机组功率调节过程中有功功率Ps可以通过转子直流电流ird来控制,而无功功率Qs可以通过转子交轴电流irq进行控制。对于实际过程中机侧变流器输出电压,稳态时转子电压有:
式中,σ=1-L2mLsLr为漏磁系数。上标ref为参考值,控制目标为:
最终DFIM功率控制框[2]见图 2,图中PI即为比例-积分调节模块,其内部控制见图 3,饱和度模块可以限制最终输出物理量的最大和最小值,在实际过程中,可以利用该模块来限制直流母线端电压。
为使实际值能够更好地跟踪参考值,外环对定子功率进行调节而内环对转子电流进行PI调节,外环PI控制器(功率调节模块)包含比例系数kpp和积分系数kip,内环PI控制器(电流调节模块)包含比例系数kpi和积分系数kii。
2 双馈式机组功率控制器参数的敏感性分析
2.1 工程概况
本文选取某抽水蓄能水电站作为工程实例,并利用水利水电工程全系统瞬变流仿真计算平台进行数值计算,在小扰动甩10%负荷工况下研究模拟变转速抽水蓄能机组的功率调节控制器参数对系统控制性能的影响。在数值计算中,机组初始状态为稳定状态,并给定转速。
水泵水轮机参数见表1,双馈感应电机参数[2]见表2。
2.2 目标函数
ITAE(Integral of Time.weighted Absolute Error)是一种在控制系统中用来评估性能的指标。它把误差的绝对值与时间相乘,然后对时间进行积分。这样做的好处是,既能够体现出误差的大小,也能反映误差收敛的速度,从而综合考虑控制精度和收敛速度的因素。
本文通过正交试验对双馈式机组的功率调节控制器参数进行敏感性分析,以评估其对系统性能的影响。采用ITAE指标作为优化目标,它的定义为:
式中 t——时间;e(t)——定子功率p和目标功率ps的误差;ts——指定的积分终点时间。
2.3 正交方案
通常来说,对于一个系统,增大比例系数kp可以加快系统响应速度、减少响应时间和静差,但会增大超调和系统不稳定性。增大积分系数ki可以消除系统静差,但也会增大超调量和系统不稳定性。合理的选择功率调节控制器参数对机组功率调节控制系统的稳定性具有重要影响。本次研究选取电流调节模块的比例系数kpi和积分系数kii,功率调节模块的比例系数kpp和积分系数kip作为正交试验设计的4个因素。极差分析是一种简单且广泛应用的分析方法[8],能够快速准确地得到优化结果。通过极差分析,能够有效地进行灵敏度的有效分析[16],评估各参数对系统性能的影响,为功率调节控制器参数的优化提供参考,具体步骤如下。
步骤一 将定子功率ps和目标功率p的误差绝对值乘以时间项再对时间的积分作为ITAE性能指标。
步骤二 根据功率控制策略,确定对计算结果的影响因素有4个,分别为kpi、kii、kpp、kip,对这4个因素进行水平设计;为了比较全面地反映这4个因素對试验结果的影响,在确定因素水平时,参数值的范围经过大量试算,双馈式抽水蓄能机组功率调节器参数值一般在(0,100)的范围内,因此kp和ki分别取值0.1、1、10、100,4组参数进行4因素4水平的正交试验。
步骤三 选择L16(44)正交表,通过正交原理设计相应的表头;确定设计方案,进行数值模拟。基于水利水电工程全系统瞬变流仿真计算平台进行不同参数的工况计算,将计算结果统计并顺序填入正交表中。
步骤四 在实践中,敏感性分析通常在稳定工况、临界工况或接近稳定工况下进行,以获得可靠且有意义的结果。在不稳定工况下,首先需要采取措施使系统恢复稳定,然后再进行敏感性分析。故对不同参数组合工况进行筛选,选出稳定工况、临界工况或接近稳定工况,再进行敏感性分析。
步骤五 选用极差分析法对筛选后试验结果统计分析,计算4个影响参数在相应的水平下ITAE指标平均值及其极差,并绘制各参数与ITAE平均值的趋势图。
步骤六 通过比较不同参数取值下的仿真结果和相应的趋势图,分析各参数对系统性能的影响。
2.4 正交试验结果分析
取正交表来设计试验,将各因素放入对应列中,经过16次数值仿真计算,试验结果见表3。
在ITAE指标值为27 258.591 1和1 314.947 4的工况下,参数组合分别为kpi=100,kii=10,kpp=1,kip=100;kpi=10,kii=1,kpp=100,kip=10。 图4、5清晰地展示了控制系统的定子功率曲线与目标功率曲线之间存在很明显的偏差,这种偏差表示了系统响应不足以满足期望,存在控制性能不佳的问题。此刻系统响应中出现剧烈的振荡,超调量过大,系统完全失稳。
在ITAE指标值为294.616 1的特定工况下,参数组合为kpi=10,kii=100,kpp=1,kip=0.1。图 6可以清晰观察到控制系统的定子功率曲线与目标功率曲线之间依旧存在明显的偏差。尽管控制系统的超调量减小,即系统的初始偏差相对较小,但是系统依旧是失稳状态,这可能意味着系统在调整过程中无法保持稳定。
在ITAE指标值为40.173 1的特定工况下时,参数组合为kpi=0.1,kii=1,kpp=1,kip=1,图7可以清晰表明在该工况下,控制系统定子功率和目标功率曲线在17 s左右重合,显示出系统响应速度较慢,存在轻微的超调,但整体系统稳定性有所改善。
在ITAE指标值等于3.214 9的特定工况下,参数配置为kpi=0.1,kii=10,kpp=10,kip=10,图 8清晰表明在该工况下,定子功率曲线和目标功率曲线在5 s左右重合,动态响应速度较快,系统在最初有轻微振荡,但超调量很小,系统动态响应品质较高。
在ITAE指标值等于0.381 4的特定工况下,参数配置为kpi=10,kii=0.1,kpp=10,kip=10,图9清晰表明在该工况下,定子功率曲线和目标功率曲线基本重合,系统稳定且动态响应速度快,系统控制性能好。
通过试验2、3、7、11、12、15这6个不同参数工况的对比,大体可以判断出当ITAE指标值小于等于40.173 15时,系统是稳定的。当ITAE指标值等于0.381 37的时候,系统相对来说拥有最好的控制性能。
由此可以得出,较小的ITAE指标值代表系统动态响应品质好,误差更小且响应速度更快,这符合良好的控制性能要求。故选取优化目标为ITAE比较合理。
2.5 功率调节控制器参数的敏感性分析
筛选出的用于极差分析的试验数据见表 4,这些数据对应于稳定工况下的试验结果。极差分析结果见表 5。
极差分析表中k表示某因素某水平时试验数据的求和,Kavg表示对应k的平均值,R表示极差值,即Kavgmax-Kavgmin。
以功率调节控制器参数的水平作为横坐标,以ITAE指标的平均值作纵坐标,绘制功率调节控制器参数与ITAE指标的趋势,见图10。
由图 10可以得到如下结论。
a)kpi的参数值在增加时,ITAE指标平均值一直呈现下降趋势,ITAE指标平均值相差幅度比kip参数值小一些。ITAE指标的平均值逐渐下降,在参数值所取水平范围内kpi取值越大越好,系统响应品质越好。
b)kii和kpp对应的ITAE指标平均值在区间范围内变化趋势不相同,但是ITAE指标平均值的极差小,系统对kii和kpp参数不太敏感。表明在一定范围内,kpp或kii参数的调整可能对系统的稳定性和性能改善影响较小。
c)随着kip参数值的增加,ITAE 指标平均值经历了不同变化阶段。在低区间(0.1~1.0),ITAE 指标平均值上升,这可能表示系统在这个范围内对于kip的变化比较敏感,导致系统响应不稳定,出现较大误差。然而,随后在(1~10)的区间,ITAE 指标平均值骤然下降,这表明对于中等范围的kip,系统的响应变得更稳定和精确。而在更高范围(10~100),ITAE 指标平均值继续下降,但变化幅度较小,对于较大的kip值,对ITAE指标平均值敏感性变低。总体来说在区间范围内,极差最大,kip对ITAE指标平均值影响最大,这表明ITAE指标平均值在目前选取的不同参数工况组合中对kip的变化非常敏感,需要仔细调整以保持系统稳定性和性能。
通过极差分析,可以得出影响ITAE指标平均值的参数主次顺序为:kip>kpi>kii>kpp,得到最优参数组合为kpi=100,kii=0.1,kpp=10,kip=100。这意味着kip对ITAE指标的影响最为显著,其次是kpi和kii,而kpp的影响最小。
综合这些分析结果,可以为功率调节控制器参数的调整和优化提供方向和依据,提高系统的运行稳定性和动态响应品质。
3 结论
本文选取某抽水蓄能水电站作为工程实例,采用正交原理进行了16组不同参数工况仿真试验,在筛选出稳定工况的基础上,分析了双馈式抽水蓄能机组功率调节控制器参数对系统控制性能的敏感性。结果表明ITAE指标值越小代表系统动态响应品质高,误差更小且响应速度更快。ITAE可以作为优化目标,评估不同参数组合对系统控制性能的影响。
极差分析结果显示,功率调节控制器参数对系统控制性能的影响顺序为kip>kpi>kii>kpp,也就是说影响系统控制性能的主次因素依次为电流调节模块的比例系数kip、功率调节模块的积分系数kpi、电流调节模块的积分系数kii、电流调节模块的比例系数kpp。
通过合理调整功率调节控制器参数,可以实现系统在特定工况下的稳定性和性能优化。之后的研究可以在本文研究基础上进一步优化相关功率调节控制器参数,这对于电力系统稳定运行具有积极的意义。
参考文献:
[1]MAHFOUD R J,ALKAYEM N F,ZHANG Y,et al.Optimal operation of pumped hydro storage.based energy systems:A compendium of current challenges and future perspectives[J].Renewable and Sustainable Energy Reviews,2023,178.DOI:10.1016/j.rser.2023.113267.
[2]胡万丰,樊红刚,王正伟.双馈式抽水蓄能机组功率调节仿真与控制[J].清华大学学报(自然科学版),2021,61(6):591-600.
[3]龚国仙,李定林,吕静亮,等.双馈式可变速抽水蓄能机组运行控制[J].大电机技术,2022(3):1-7.
[4]谢宁宁.交流励磁抽水蓄能机组最优功率控制及参与调频策略研究[D].重庆:重庆大学,2022.
[5]SCHMIDT J,KEMMETMUELLER W,KUGI A.Modeling and static optimization of a variable speed pumped storage power plant[J].Renewable Energy,2017,111:38-51.
[6]BIDGOLI M A,YANG W,AHMADIAN A.DFIM versus synchronous machine for variable speed pumped storage hydropower plants:A comparative evaluation of technical performance[J].Renewable Energy,2020,159:72-86.
[7]SARASUA J I,PEREZ J I,WILHELMI J R,et al.Dynamic response and governor tuning of a long penstock pumped.storage hydropower plant equipped with a pump-turbine and a doubly fed induction generator[J].Energy Conversion and Management,2015,106:151-164.
[8]徐超,葉观宝.应用正交试验设计进行数值模型参数的敏感性分析[J].水文地质工程地质,2004(1):95-97.
[9]叶建和,李承军,吴迪,等.改进正交试验法在调速器参数优化中的应用[J].水电与新能源,2011(3):6-8.
[10]罗敏,王玉凤.水轮机调速系统选型及PID正交优化设计[J].科技创新导报,2008(20):54-55.
[11]金波,朱世强,张光琼,等.用正交试验法整定PID控制器参数[J].中国机械工程,2000(6):91-92.
[12]彭安华,孙旭东,王智明.基于正交试验法的PID控制器参数整定[J].机械科学与技术,2011,30(6):1028-1032.
[13]李路.基于AHP-正交试验模型围岩稳定性影响因素数值模拟研究[J].人民珠江,2021,42(8):55-61.
[14]贾雪慧.平原水库土石坝的地震动力响应敏感性分析[J].人民珠江,2019,40(5):18-23.
[15]GONZALO A,JESS L,MIGUEL R,et al.Doubly fed induction machine[M].IEEE Press,2011.
[16]田原.极差分析法在北方冬季水利工程施工期影响因素灵敏度分析中的应用[J].水利技术监督,2019(2):160-163.
