基于GA.GRNN地应力场反演的超长深埋隧洞围岩稳定性研究
2024-02-18郭冲王翰盛邓伟杰赵顺利杜卫长
郭冲 王翰盛 邓伟杰 赵顺利 杜卫长
摘要:基于超长距离引调水工程地质条件及实测地应力资料,建立了工程引水线路初始地应力场三维反演计算模型。通过遗传算法优化广义回归神经网络方法(GA.GRNN),较为准确地反演了工程引水线路的初始地应力场。基于初始地应力场,对长距离引水线路地应力进行分区,并在各分区选择典型断面进行隧洞围岩稳定分析。研究结果表明:工程区应力场以多隆沟断裂带为界,西侧为水平构造应力区,极高地应力区和高地应力区多分布于地质构造带附近,需注意应力释放导致的岩爆发生;多隆沟断裂带东侧为自重应力区,中等地应力区多分布于此,围岩稳定性相对较好。
关键词:初始地应力;神经网络;遗传算法;围岩稳定
中图分类号:TV672+.1 文献标识码:A 文章编号:1001.9235(2024)01.0103.11
Research on Stability of Utralong and Deep.Buried Tunnel Surrounding Rocks Based on GA.GRNN Geostress Field Inversion
GUO Chong1,2,WANG Hansheng3,DENG Weijie1,2,ZHAO Shunli1,2,DU Weichang1,2
(1.Jianghe Engineering Inspection and Testing Co.,Ltd.,Zhengzhou 450003,China;
2.Yellow River Engineering Consulting Co.,Ltd.,Zhengzhou 450003,China;
3.Hangzhou Huajin Lianzhe Intellectual Property Agency Co.,Ltd.,Hangzhou 310051,China)
Abstract: According to the geological condition and measured geostress data of the utralong.distance water diversion project,a 3D inversion calculation model of the initial geostress field of the water diversion route was established.The initial geostress field of the water diversion route was exactly simulated through the method of generalized regression neural network (GRNN) optimized by genetic algorithms (GA.GRNN).Based on the initial geostress field,the geostress of the water diversion route was partitioned,and the stability of the tunnel surrounding rocks in typical sections was analyzed.The research results show that the geostress field is bounded by Duolong gully fault belt,and the west of the fault belt is a horizontal tectonic stress area.Extremely high and high geostress areas are distributed in geological structural belts where attention should be paid to rock bursts caused by stress release.The east of the Duolong gully fault belt is the self.weight stress area,and the moderate geostress area is distributed here.The stability of the surrounding rocks here is relatively good.
Keywords:initial geostress;neural networks;genetic algorithms;stability of surrounding rocks
地应力是赋存于岩体内的天然应力,对工程的设计、施工具有重要意义[1-3]。工程中地应力原位测量是提供岩体初始地应力最直接、有效的手段[4]。但由于地应力场成因复杂多变,测点相对分散,地应力实测结果往往具有一定的离散性,难以体现整个工程区地应力场的宏观规律。特别是对于超长距离引调水工程,由于场地、经费等客观条件限制,不能进行大规模、全范围的原位测量。因此,需要在实测地应力资料的基础上,结合实际工程地质条件,通过有效的分析方法进行反演计算,以获得范围更大、适用范围更广的初始地应力场[5-7]。
目前,相关科研工作者针对初始地应力场的反演分析开展了一定的研究工作,以多元回归法为主,如张建国等[8]、裴启涛等[9]采用多元回归法,对工程地应力场反演進行了深入研究。多元回归法地应力状态表达式较为单一,能较好地适用于小范围的地应力场反演,如水电站地下厂房、穿山公路隧洞、边坡、煤层巷道开挖的地应力反演。而对于超长距离的引调水工程,引水隧洞穿越多地层和应力区,应力状态错综复杂,单一的应力表达式无法完全表示工程区全段的应力状态,适用性有限。随着计算机技术的发展,灰色理论、神经网络法、遗传算法等智能方法被应用于岩体初始地应力场的反演计算。如戚蓝等[10]将系统工程灰色理论引入到地应力场分析中;裴书锋等[11]、马玉岩等[12]、陈正林等[13]将人工神经网络应用于地应力场的反演计算;张金[14]、杨志强等[15]、谢学斌等[16]基于遗传算法开展了岩体初始应力场反演研究。但传统的神经网络和遗传算法在反演计算中存在精度和效率上的不足,因此有必要建立一种适用于长距离引调水工程的考虑多重地质因素、计算效率高的反演计算方法。
针对隧洞围岩稳定性研究,科研工作者建立了Mohr.Coulomb、Drucker.Prager、概率强度、非线性统一等围岩强度准则[17-20]和容许位移、容许位移速率、变形速率比等变形准则[21-23],以及围岩松动圈理论、围岩局部失稳监控指标体系、围岩开挖位移预警值等围岩破裂区判据等[24-26]。针对高水平构造应力区深埋超长隧洞的围岩稳定性研究相对较少,当前研究的重点大多集中在自重应力的影响上。同时地应力分区标准和研究断面的选取较为粗略,并不完全适用于超长引调水工程。因此,有必要对工程沿线地应力场进行细化分区研究,并基于地应力分区结果和地层岩性对隧洞典型断面进行精准围岩稳定分析。
基于此,针对长距离引水工程地质条件及实测地应力资料,建立引水线路初始地应力场三维反演计算模型,通过遗传算法优化神经网络方法(GA.GRNN),反演计算工程引水线路的初始地应力场。基于初始地应力场,对长距离引水线路地应力进行细化分区,并在各分区选择典型断面进行隧洞围岩稳定分析,为工程的设计和施工提供重要依据。
1 高水平构造应力区地应力实测
1.1 工程概况
青海省某超长距离引调水工程由引水工程和供水工程组成,工程区位于青藏高原东北部,海拔高度多在2 500~3 000 m以上。日月山、野牛山、拉脊山自西北向东南斜贯工程区。区域内地形地貌主要有构造剥蚀、侵蚀高山-中高山、构造侵蚀中山丘陵和侵蚀堆积河谷三大地貌单元。工程位于青藏高原东北部构造带,地处祁连、青海南山-拉脊山两大山系的交接处,区域大地构造上属祁连中间隆起带、南祁连褶皱带及秦岭褶皱带内。受多条构造带的影响,工程区域内地应力场分布较为复杂。
1.2 水压致裂法地应力测试
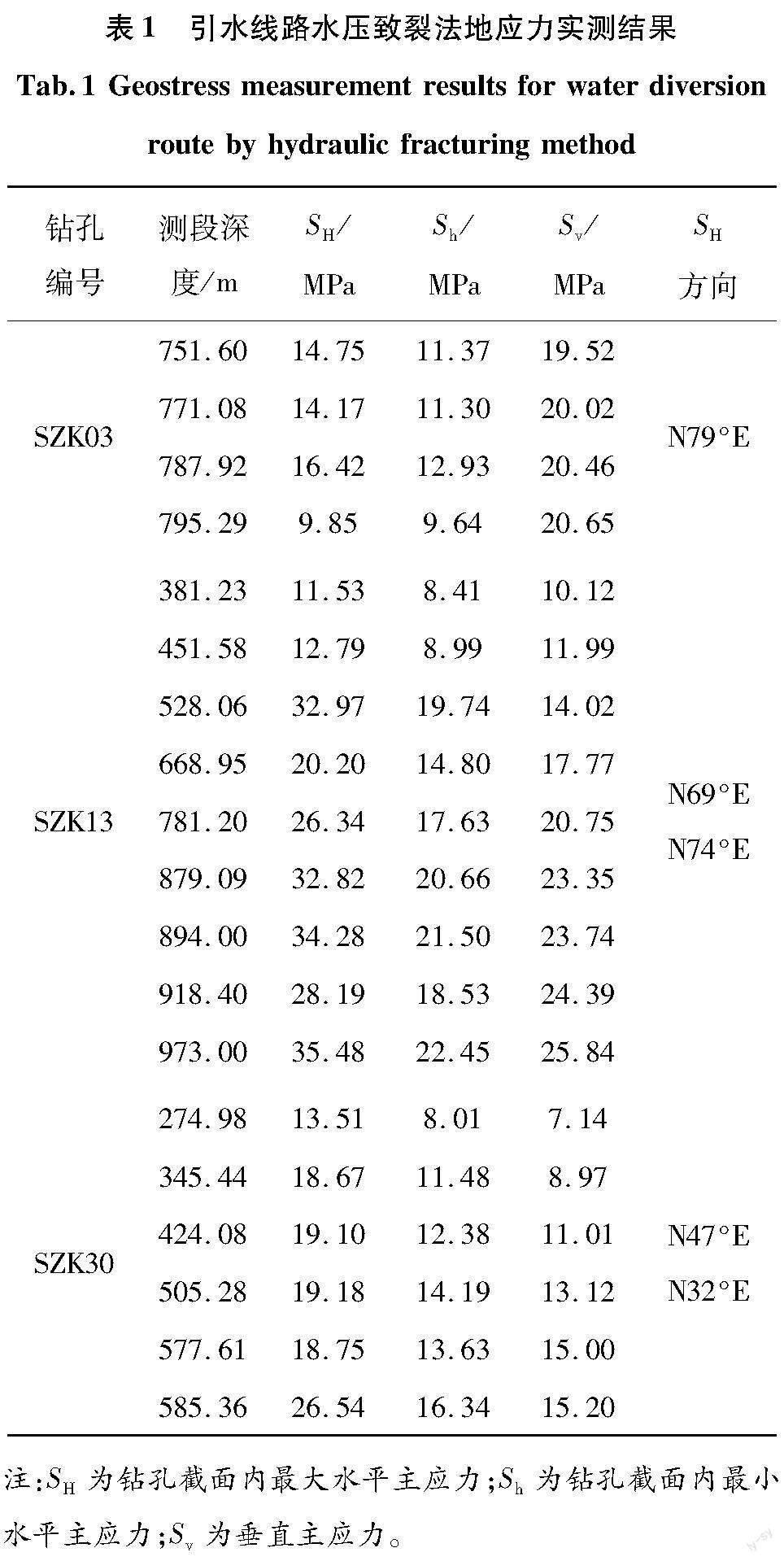
在工程引水线路开展了SZK03、SZK13和SZK30的水压致裂法地应力测试工作,地应力实测结果见表1。
水压致裂法地应力实测结果表明,工程测试区域内SH范围为9.85~35.48 MPa,Sh范围为8.01~22.45 MPa,最大水平主应力方向为N32°~79°E,应力场状态以NE~NEE向挤压为主。
SZK13和SZK30工程区域地应力分布规律为SH>Sv≈Sh,区域内应力以水平构造应力为主,区域构造作用比较强烈;SZK03工程区域地应力分布规律为Sv>SH>Sh,区域内应力以垂直应力为主,为自重应力区,表明工程引水线路地应力场的复杂性。
2 基于GA.GRNN的地应力反演分析模型
2.1 初始地应力场反演计算原理
地应力反演原理[9]是将地应力回归计算值k作为因变量,把数值计算求得的自重应力场和构造应力场相应于实测点的应力计算值σik作为自变量,回归方程的形式为:
n——工况数。
对于m个观测点,最小二乘法残差平方和为:
式中 σ*jk——k观测点j应力分量的观测值;σijk——i工况下k观测点j应力分量的数值计算值;j=1~6,对应初始应力的6个分量。
解此方程,得n个待定回归系数L=(L1,L2,…,Ln)T,则计算域内任一点P的回归初始应力σjp,可由该点各工况计算值迭加而得:
2.2 遗传算法优化神经网络(GA.GRNN)
广义回归神经网络(GRNN)[11]是径向基网络的一种变形形式,可自动建立输入和输出的高维非线性映射,在解决复杂的非线性问题时,不需要假定具体的函数形式,从而大大简化了求解的难度。广义回归神经网络预测结果的好坏依赖于基函数光滑因子的选取,由于地应力变化规律不确定,无法用函数定向地确定光滑因子的最佳值,且试算法计算量较大,无法保证精度要求。遗传算法[14]是一种全局最优化方法,适用于多极值点的优化问题,将选择、交叉、变异等概念引入到算法中,通过构成一组初始可行解群体并对其进行操作,使其逐渐移向最优解。为此,引入遗传算法,对光滑因子可能的取值进行全局搜索,自动搜索最优光滑因子参数值。通过把遗传算法和广义回归神经网络结合到一起,构建出GA.GRNN方法,计算流程见图1。
采用遗传算法搜索最优光滑因子,建立GA.GRNN模型,其具体步骤如下:①对样本数据进行归一化预处理;②确定遗传算法参数;③遗传算法初始化,生成初始种群;④GRNN读入学习样本进行网络训练,按给定的适应度函数进行适应度评价;⑤遗传算法按照每个个体的适应度大小进行选择、交叉和变异操作,得到新的种群;⑥判断是否达到最大进化代数,若已达到,则停止计算,返回适应度最高的个体;否则转至步骤④,直到达到最大进化代数;⑦输出适应度最高的个体对应的实值数,即为最优的光滑因子;⑧用最优光滑因子建立GRNN模型,对测试样本进行预测,得到预测结果;⑨对预测数据进行反归一化,对GRNN网络性能进行评估,并存储数据。
2.3 计算范围及计算模型
通过分析该工程区水文地质、工程地质条件和实测地应力测点的分布情况,建立反演分析计算模型。将引水隧洞线路方向设为X轴,垂直隧洞线路方向设为Y轴,竖直向上为Z轴。计算范围为:X轴方向取30 000 m,Y軸方向取2 500 m,Z轴方向为海拔2 300 m至地表。
计算模型考虑引水隧洞沿线穿越的8条断层,包含4条较大的断裂:多隆沟断裂(F1)、青海南山南缘断裂(F2)、青海南山北缘断裂(F3)、倒淌河—循化断裂(F4)。工程区主要地层岩性分别为:印支期中三叠世花岗闪长岩(γδT2)、印支期中三叠世花岗闪长岩(ηγT2)、新近系贵德群(Ng)灰褐桔红色砂砾岩、早中三叠系隆务河组(T1l)青灰色砂岩板岩互层夹灰岩、加里东期(γS.O3)灰白色花岗岩、中三叠系香阿洞组(T2x)灰-深灰色砂岩板岩夹灰岩、第四系上更新统洪积(Qpl3)角砾、砂、黄土状亚砂土及黄土。数值模型采用四面体单元,模型网格单元数为426 182,节点数为80 543,区域三维模型和实体模型见图2。
2.4 模型参数选取及边界条件
反演计算过程中采用线弹性模型,根据工程勘察试验结果,同时参考工程地质勘察报告中第四系松散层孔隙潜水、基岩裂隙水及相关钻孔水位特征等信息,在选取计算参数时,有针对性地将部分参数参考试验结果中的饱和状态进行参数取值。计算采用的岩石基本参数见表2。
工程引水线路较长,跨越多个地质构造带,地应力场分布规律较为复杂,回归岩体初始应力场的7种基本因素见图3。
通过查阅均匀设计表,确定包括自重影响系数在内的边界条件一共7个参数,每个参数分为28个水平。根据遗传算法求得广义回归神经网络的最优光滑因子为0.553 8,分别代入实测点SZK30、SZK03和SZK13归一化处理后的数据,得到的模型边界条件见表3。
3 初始地应力反演结果
3.1 反演结果比较分析
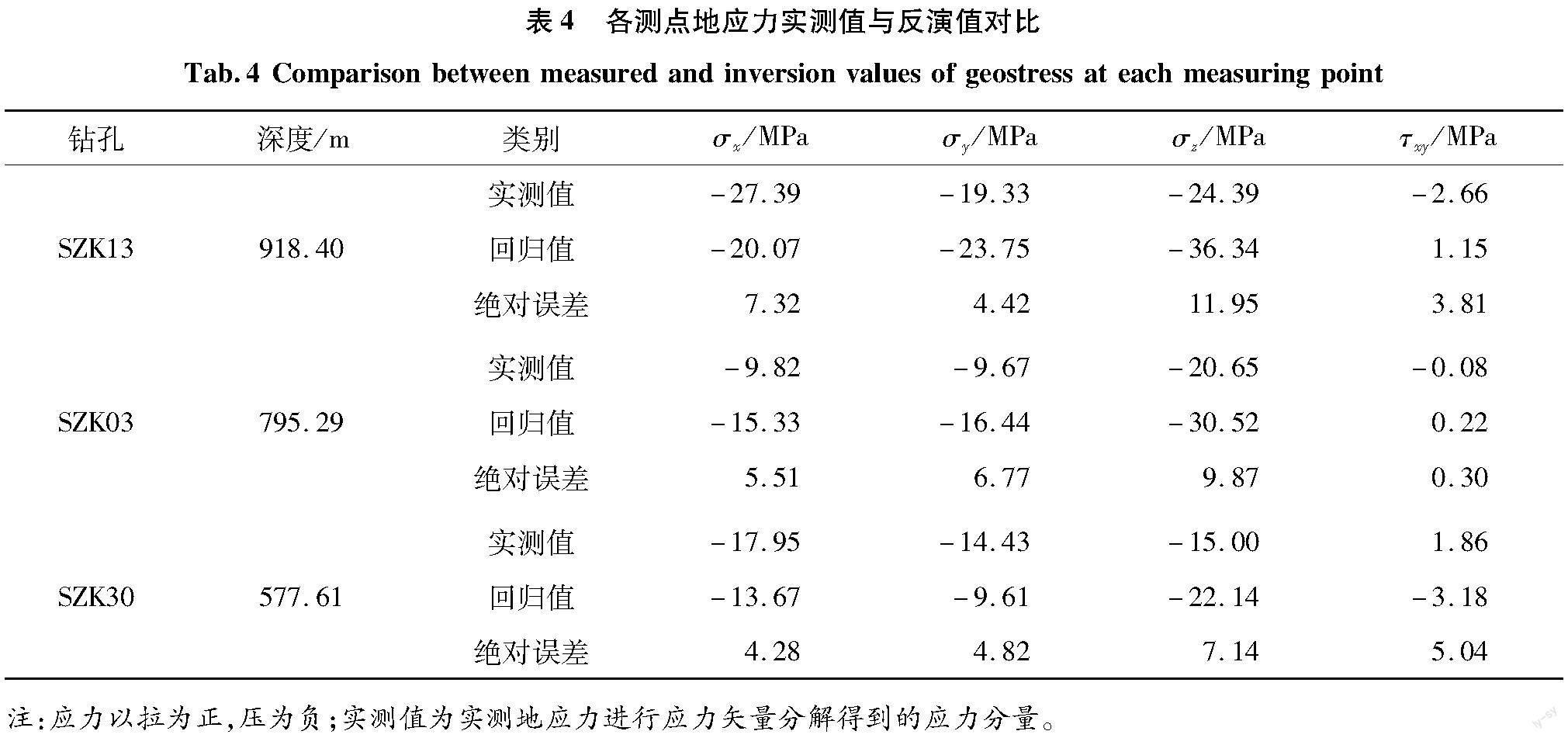
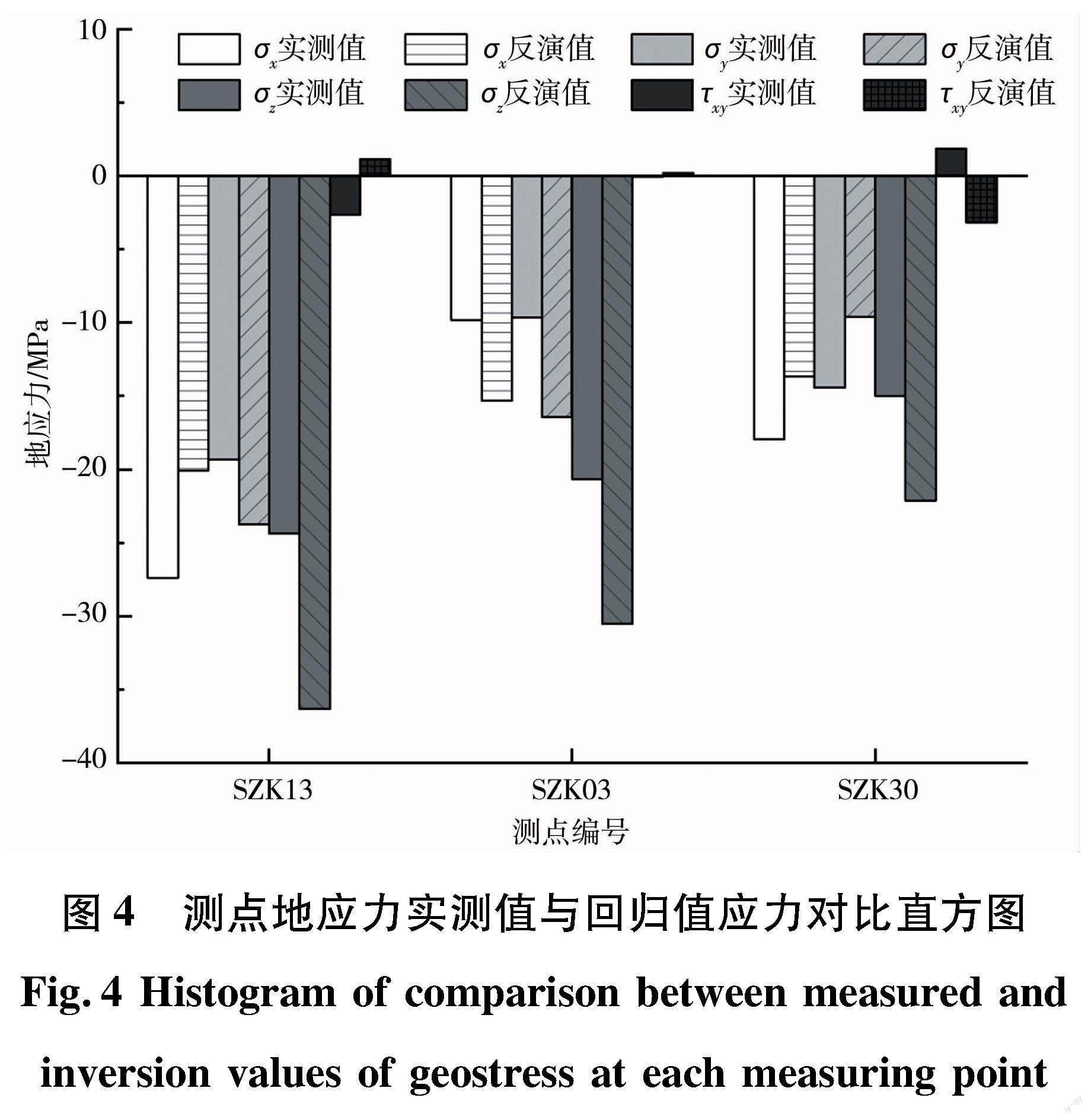
将边界条件代入数值分析模型进行计算,获得模型各地应力分量,与实测结果对比见表4和图4。
由表4和图4可以看出,大部分测点地应力分量的反演值与实测值在数值上较为接近,应力分量平均绝对误差为5.94 MPa,误差相对较小。另外,相较于水平应力分量,垂直应力分量的误差相对较大,且回归值均高于实测值,这是由于垂直应力受地形地貌、历史应力、构造作用等综合因素的影響,其值一般为岩体自重应力和地质构造垂直应力叠加的结果,而水压致裂法仅能测量水平主应力,表中所列垂直应力分量实测值为根据上覆岩体厚度进行的估算值,其值均小于实际垂直应力。总的来说,反演结果与现场试验测试结果和历史地质构造资料中的地应力场一般规律相符,可较好地模拟工程引水线路的初始地应力场。
3.2 工程引水线路初始地应力场分布规律
基于GA.GRNN方法反演结果,对工程引水线路区域地应力进行反演合成计算,截取引水隧洞轴线纵剖面的最大主应力、中间主应力和最小主应力,见图5。引水隧洞沿线区域初始地应力场最大主应力范围为15~30 MPa,中间主应力范围为10~20 MPa,最小主应力范围为10~20 MPa。
引水隧洞轴线纵剖面的地应力矢量分布见图6。由6a可以看出,构造应力方向与隧洞轴线方向近平行,引水隧洞沿线最大主应力矢量以多隆沟断裂为界分为2个区域:第一区域为多隆沟断裂以西的闪长岩一区,以水平构造应力为主,构造应力方向与隧洞轴线方向近平行,为构造应力发育区;第二区域为多隆沟断裂以东的砂岩、板岩互层区和青海南山北缘断裂带(F2)东部闪长岩二区,以自重应力为主,为自重应力区。反演所用测点SZK30位于闪长岩一区,测点SZK13位于闪长岩二区的F3断裂区,二者均以水平构造应力为主,测点SZK03位于闪长岩二区,以自重应力为主,反演计算地应力方向与实测地应力方向基本吻合。
4 高水平构造应力区隧洞围岩稳定分析
4.1 地应力分级
初始地应力的判别与划分,采用DL/T 5419—2009《水电水利工程地下建筑物工程地质勘查技术规程》中考虑地应力大小与强度应力比的综合分级方案,强度应力比计算见式(4)。
式中 Rb——岩石饱和单轴抗压强度,MPa;σm——最大主应力,MPa。
岩体初始地应力分级方案见表5。
基于地应力反演所得初始地应力场,提取引水隧洞沿线地应力数值,统计各测点岩体的强度应力比,并根据地应力分级方案对引水隧洞沿线地应力进行分区,结果见图7。
根据图7的统计结果,将隧洞沿线地应力按地层进行分类,结果见表6。
由表6可知,引水线路极高地应力区主要集中在断层附近,典型断面如7.8~8.4 km的闪长岩段,局部初始地应力达59.6 MPa。高地应力区分布范围较广,典型断面如2.2~7.6 km和20.6~25.2 km的闪长岩段、8.8~11.6 km的花岗岩段、12.2~20.0 km和25.4~29.0 km的砂岩板岩互层段,初始地应力水平主要集中于20.0~50.0 MPa。中等地应力区主要集中分布于1.6~2.0 km和21.8~23.4 km的闪长岩段,其初始地应力水平相对较低。
4.2 隧洞围岩稳定计算模型
隧洞开挖对应力场的扰动主要集中在一定范围内,通常不超过3倍洞径。利用反演计算的初始地应力场评价隧洞围岩稳定时,在数值建模过程中,应建立足够大的边界,按3倍洞径考虑,提取典型断面处的初始应力场应力值,作为围岩稳定分析的应力边界条件。
选取3种地应力分区下隧洞的典型断面(8.4 km;20.8、11.0、15.0 km;22.0 km)进行隧洞围岩稳定分析。计算模型尺寸为100 m×50 m×50 m,共112 000个单元,119 700个节点。计算采用莫尔-库伦力学模型和应力边界条件,加载时初始化岩体内部的赋存应力,并施加边界条件。根据工程勘察试验结果和初始应力场反演结果,围岩基本参数和初始地应力见表7。
4.3 隧洞典型断面围岩稳定分析
根据地应力分区结果,在引水线路中选取典型断面进行围岩稳定分析,以此评价施工期围岩的安全性,并为保障引水隧洞的安全与快速施工提供数据支撑。
4.3.1 极高地应力区(8.4 km)
本区域所选的典型断面为测点8.4 km处闪长岩断面。隧洞开挖后围岩的位移场、最大主应力见图8。隧洞开挖后,围岩最大变形为0.22 m,围岩最大主应力高达65.0 MPa,未出现拉应力,受偏应力的作用,最大主应力出现偏转,普遍集中于拱顶偏左和拱底偏右位置。鉴于围岩应力较高,建议隧洞开挖时注意应力释放导致的岩爆发生,同时在岩体应力释放后及时支护,防止围岩塑性区向深部扩展。
4.3.2 高地应力区(20.8、11.0、15.0 km)
高地应力区闪长岩段(20.8 km)隧洞开挖后围岩的位移场、最大主应力见图9。洞段开挖后,围岩最大变形为0.13 m,围岩最大主应力为52.0 MPa左右,未出现拉应力。受偏应力的作用,最大主应力的位置出现近45°的偏转,普遍集中于拱顶偏右和拱底偏左位置。
高地应力区花岗岩段(11.0 km)隧洞开挖后围岩的位移场、最大主应力见图10。洞段开挖后,围岩最大变形为0.12 m,该洞段围岩最大主应力为36.0 MPa左右,未出现拉应力。
高地应力区砂岩与板岩互层段(15.0 km)隧洞开挖后围岩的位移场、最大主应力见图11。洞段开挖后,围岩最大变形为0.20 m,洞段围岩最大主应力为47.0 MPa左右,未出现拉应力。受偏应力影响,拱顶和拱底的最大主应力小于拱腰。
高地应力区围岩应力较高,建议隧洞开挖时注意应力释放导致的岩爆发生,并及时支护,防止塑性区扩展和应力松弛引发的掉块。
4.3.3 中等地应力区(22.0 km)
中等地应力区闪长岩段(22.0 km)隧洞开挖后围岩的位移场、最大主应力见图12。洞段开挖后,围岩最大变形为0.11 m,围岩最大主应力为46.0 MPa左右,未出现拉应力。最大主应力变化明显,受水平挤压作用,隧洞拱顶偏左和拱底偏右处应力逐渐递减至20.0 MPa。鉴于围岩变形较小,测点22.0 km处闪长岩区隧洞围岩安全性较好,岩体基本能够实现自稳。
5 结论
结合高水平构造应力区长距离引水工程地质条件及实测地应力资料,建立引水线路初始地应力场反演计算模型,通过遗传算法优化神经网络方法反演得出工程引水线路的初始地应力场。对引水线路地应力进行细化分区,并在各分区选择典型隧洞断面进行围岩稳定分析。通过研究得到如下结论。
a)地应力反演结果表明,引水隧洞沿线区域初始地应力场最大主应力范围为15~30 MPa,约为最小主应力的1.5倍。构造应力方向与隧洞轴线方向近平行,工程区应力场以多隆沟断裂带为界,西侧以水平构造应力为主,东侧以自重应力为主。地应力反演回归值与实测值较为吻合,为引水隧洞的设计和施工提供了合理的三维初始地应力场。
b)地应力分区研究表明,极高地应力区多出现在地质构造带附近;由于隧洞埋深大,地质构造作用强烈,隧洞大部分区域处于高地应力区;中等地应力区主要分布于工程东侧的自重应力区,初始地应力水平相对较低。
c)根据地应力分区结果,开展了引水隧洞典型断面的围岩稳定分析,断裂带附近的极高地应力区和分布范围最广的高地应力区段隧洞围岩应力较高,变形较大,需注意应力释放导致的岩爆发生,并及时支护,防止塑性区扩展和应力松弛引发的掉块。中等地应力区段围岩变形较小,岩体基本能够实现自稳,围岩稳定性相对较好。
参考文献:
[1]周亚萍,姜海波.深埋高地应力水工隧洞地应力特征及岩爆脆性破坏深度预测研究[J].隧道建设(中英文),2022,42(S1):321-330.
[2]王琛涛.深埋隧洞高地应力岩体破坏型式研究及防治措施[J].水利规划与设计,2022(7):81-86,103,138.
[3]王超,王益腾,韩增强,等.垂直孔应力解除法地应力测试技术及工程应用[J].岩土力学,2022,43(5):1412-1421.
[4]王成虎.地应力主要测试和估算方法回顾与展望[J].地质论评,2014,60(5):971-991,996,992-995.
[5]周朝,尹健民,董志宏,等.考虑边界荷载作用方向的特长隧道初始应力场分区反演方法[J].岩石力学与工程学报,2022,41(S1):2725-2734.
[6]王金安,李飞.复杂地应力场反演优化算法及研究新进展[J].中国矿业大学学报,2015,44(2):189-205.
[7]赵雨,白金朋.基于FLAC3D的多元线性回归法地下厂房初始地应力场反演重构[J].水电能源科学,2022,40(3):149-152,185.
[8]张建国,张强勇,杨文东,等.大岗山水电站坝区初始地应力场反演分析[J].岩土力学,2009,30(10):3071-3078.
[9]裴启涛,李海波,刘亚群.南水北调西线工程坝区初始地应力场反演分析[J].岩土力学,2012,33(S2):338-344.
[10]戚藍,崔溦,熊开智,等.灰色理论在地应力场分析中的应用[J].岩石力学与工程学报,2002,21(10):1547-1550.
[11]裴书锋,赵金帅,于怀昌,等.考虑洞室岩体应力型破坏特征的局部地应力反演方法及应用[J].岩土力学,2020,41(12):4093-4104.
[12]马玉岩,沈阳,侯东奇.基于人工神经网络和地层剥蚀原理的地应力场反演研究[J].水电站设计,2021,37(3):1-5,12.
[13]陈正林,何国志,张劼超,等.小样本数据下三维地应力反演分析[J].科学技术与工程,2022,22(22):9822-9829.
[14]张金.遗传算法在地应力反演中的应用[D].青岛:中国石油大学,2010.
[15]杨志强,高谦,翟淑花,等.复杂工程地质体地应力场智能反演[J].哈尔滨工业大学学报,2016,48(4):154-160.
[16]谢学斌,罗海霞,杨承祥,等.基于遗传单纯形算法与RBF网络的地应力场反演方法[J].铁道科学与工程学报,2015,12(1):72-78.
[17]甘玉叶,郑小燕.Hoek.Brown准则中参数不同选取值对Mohr.Coulomb参数值的影响[J].科学技术与工程,2012,12(21):5379-5383.
[18]王彬,荣传新,程桦,等.基于DP准则双排管冻结壁力学特性理论分析[J].科学技术与工程,2016,16(25):44-50,62.
[19]乔建刚,彭瑞,李景文,等.基于修正莫尔库伦的基坑开挖对隧道安全影响研究[J].中国安全生产科学技术,2022,18(2):177-183.
[20]周凤玺,邵彦平,甘东彪.基于广义非线性统一强度理论的隧道塌落拱分析[J].应用力学学报,2020,37(2):682-688,935-936.
[21]黄海.九绵高速公路可溶岩隧道施工期围岩位移控制基准研究[D].成都:成都理工大学,2020.
[22]钟放平,张伟,宫凤强,等.山岭公路隧道围岩稳定性的位移判别分析方法[J].公路工程,2008,33(6):91-94.
[23]李世煇,宋军.变形速率比值判据与猫山隧道工程验证[J].中国工程科学,2002(6):85-91.
[24]苏士龙,高海海,周康乐.基于统一强度理论的巷道围岩松动圈计算方法[J].科学技术与工程,2020,20(27):11045-11050.
[25]李美晨,赵启峰,程志恒,等.巷道围岩失稳垮冒风险等级分类与差异性分级管控[J].煤炭技术,2021,40(11):106-109.
[26]沈才华,古文博,李鹤文,等.基于损伤扩容理论的圆形隧洞围岩松动圈位移计算方法[J].隧道建设(中英文),2019,39(1):40-47.
