基于信噪比系数的双阈值分布式协作算法的研究*

李展雄，刘丽萍，方 亮，吕佳枫，王 赐

（宁夏大学 电子电气工程学院，宁夏 银川 750021）

0 引言

信息技术的快速发展使得无线通信业务的需求量不断增大，而每种无线通信技术均需要一定的频谱资源作为支持，这使得频谱资源匮乏的问题更加严峻。为了解决该问题，认知无线电(Cognitive Radio，CR)技术[1−2]应运而生。认知无线电技术主要通过认知用户在授权频段进行频谱感知后发现空闲频段，即频谱空洞，在保证授权用户高质量通信的前提条件下，可以暂时接入该频段进行通信，以此改善频谱资源过度使用的情况[3]。频谱感知[4]是认知无线电技术中的核心任务，而频谱感知中能量检测算法具有操作简单、计算简便、灵活性强等优势，被研究学者广泛使用[5−9]。然而，在信噪比较低的环境下，能量检测容易受到噪声不确定性的影响使得系统的检测效果不佳，因此在文献[10]中，鲁春燕等人提出了一种基于噪声不确定性的双门限协作能量检测算法，通过理论分析与仿真实验表明所提算法对环境的适应能力更强，在一定程度上减少了噪声不确性给整个系统带来的影响，同时也实现了频谱的高效利用。在文献[11]中，冉超等人搭建了一套软件无线电系统在真实信道中进行实验，并提出一种改进的双阈值能量检测算法。该算法是在不可信区间内加入一个细化阈值，对判决结果进行融合，同时对授权用户的频谱使用情况进行实时检测，通过仿真结果证明该算法在信噪比较低的情况下具有更高的检测概率。

另外，也考虑到在实际通信中由于存在多径效应、阴影效应等影响，为了更好地达到预期效果，在文献[12]中，刘会衡等人提出了一种双门限协作能量检测算法，该算法是针对于不可信区间内的信号统计量，采用了一种最大比合并的方式，以此来提高感知结果的准确度与可信度。在文献[13]张学军等人提出了一种基于信任度的双门限协作频谱感知算法，该算法是通过认知节点的效能函数求得最优的双门限，然后对认知节点进行本地能量检测。在文献[14]中，首先提出了两种基于信号最大特征值和能量的增强检测算法，在保持两种算法优点的同时实现系统性能的提升。为了使所提出的算法更加实用，提出了另外两种基于未知噪声方差的最大似然估计的新盲谱感知算法。在文献[15]中，作者提出了一种基于动态匹配的双门限频谱检测算法。该算法可以通过动态阈值的设置和数据匹配来检测传感数据，减少恶意数据的影响并使最终的传感结果更加准确。仿真结果表明，所提出的算法能够降低虚警概率和漏检概率来提高检测概率。在文献[16]中，作者提出了一种动态的双阈值方案以及融合中心的协作频谱感知。动态阈值选择通过创建噪声方差历史来处理实际情况下的噪声不确定性参数。通过仿真实验证明，使用所提出的方案在信噪比为−22 dB 和虚警概率为0.5 时检测概率提高了20%。考虑到传统算法因阈值固定不变导致低信噪比时系统的检测概率不佳以及集中式协作在特殊场合下难以实现等问题。本文创新点如下：

（1）感知用户根据信噪比系数来自适应地调整双门限的值。

（2）针对在特殊场合集中式协作的方法不能够使用的问题，采用分布式的协作方式，即首先将每个认知用户感知到的信息进行交换并进行一致滤波处理，然后采用OR 融合准则进行最终的判决。

1 系统检测模型

能量检测算法可以用一个二元假设模型[17]来表示，输入时域信号y(t)，经过滤波、A/D 转换后，对采样值求模、取平方和求和等操作，最后将得到的检测量与门限值T进行比较，得到当前频段的使用状况，其检测流程如图1 所示。

图1 能量检测原理框图

根据认知用户检测到的能量统计值可建立以下模型：

在这种检测模式中，y(t)代表认知无线电接收到的信号，n(t)代表加性高斯白噪声，h(t)代表通道增益，x(t)代表授权用户所发出的信息。在通信信道中，H1代表当某个频段正处在被授权用户占用阶段；H0则代表当某个频段的授权用户不存在，该频段正处在空闲阶段，代表认知还可以接入。检测到的能量统计值可表示为：

式中，K为采样点数；R(K)为接收信号序列的第K个采样信号。同样地，双阈值检测和单门限能量检测算法的基础原理是一致的。不同的是，双阈值频谱检测设置了两个高低不同的阈值λH和λL来尽可能地减少噪声不确定性所带来的影响，如果检测到的信号能量值落在[λH,λL]区间，此时暂不进行判决。双阈值频谱检测的判决规则如下所示：

假设在加性高斯白噪声的信道环境下，采样点数较大的情况下，能量统计值可近似服从下式的高斯分布[8]：

式中，λ为系统的判决阈值，Q函数表示互补累计分布函数。

基于文献[9]中，在信噪比较低的环境下，信道中的噪声不再是理想的AWGN，而是在一定范围内持续的波动。假设虚警概率和漏检概率一定时，根据式（5）和式（6）可以得出两个高低判决门限为：

2 具体算法设计

2.1 算法网络模型

在分布式协作能量检测中，认知用户的网络模型如图2 所示。

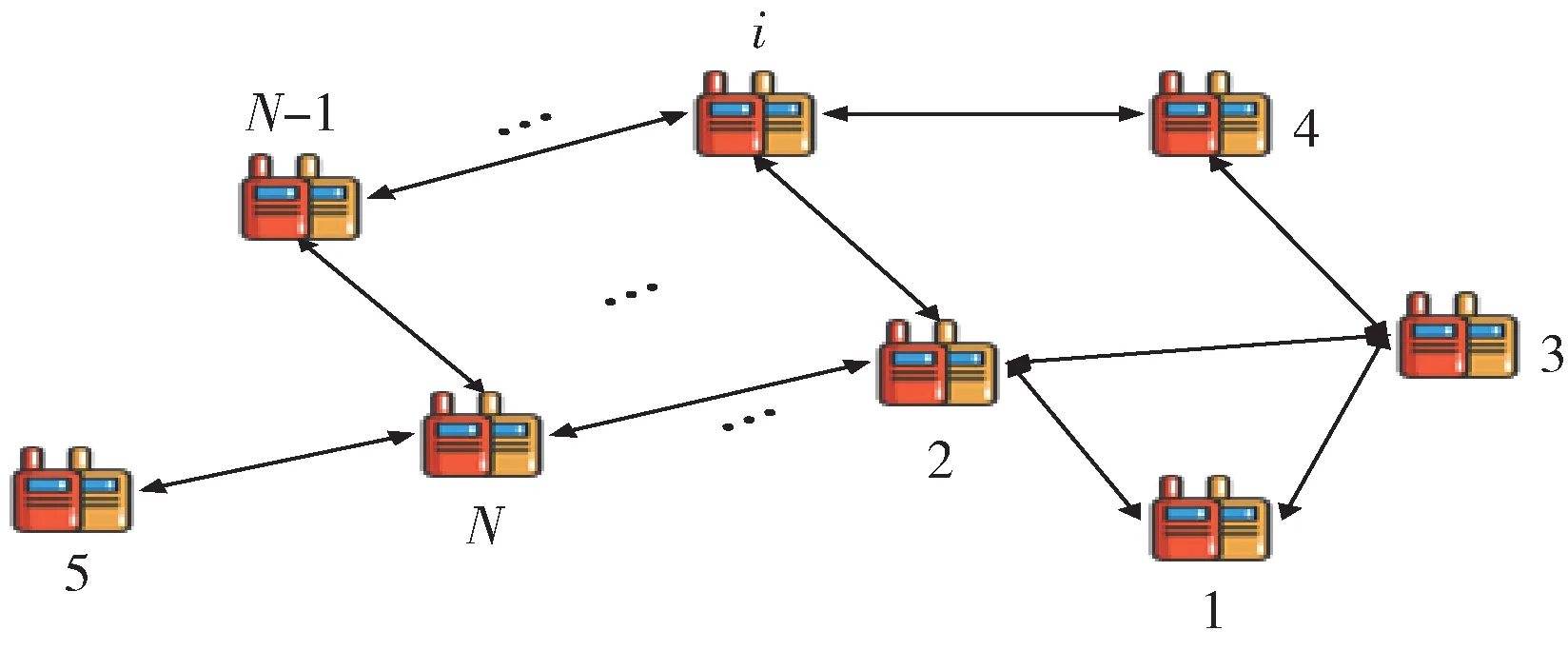
图2 具有N 个认知用户的分布式协作模型

根据图2 所示，现定义Q={1,2,…，N}为节点的集合，来表示所有的感知用户。其中V={(i,k)|i,k∈Q}作为边集，用来表示每个感知用户之间可以互相通信的节点个数，即有效的通信链路。Ni={(k∈Q)|(i,k) ∈V} 表示节点i的相邻节点的集合，di表示相邻节点的个数。本文研究的分布式协作是连通的，也就是任意两个节点之间至少存在一条直接或者间接的信息路经，同时两个相邻节点的信息都是互通的[10]。

2.2 流程设计

传统的双阈值检测是根据接收到能量统计值T与两个固定门限值比较，如果大于λH，则判定授权用户正在使用该频段；如果小于λL，则判定该频段处于空闲状态，可供认知用户暂时接入；如果处于[λH,λL]之间，则暂时不进行判决。现根据高低判决门限和分布式协作能量检测的原理进行具体流程设计，假设每个感知用户节点的工作参数在一定时间内不变且相同，完成一次检测的情况下，可以得到自适应双阈值协作能量检测算法的流程如下：

（1）由式（7）和式（8），通过一个用户的虚警概率、漏检概率以及噪声功率求出高低判决门限值，此时每个感知用户的门限值都相同。

（2）各认知用户将接收到的信号功率转换为信噪比并计算出信噪比系数,如式（9）所示：

其中,Κi表示第i个认知用户的权重，N表示认知用户的个数，SNRi表示感知用户接收到授权用户信号的信噪比。接着根据求得的高低门限值计算所得结果，调整判决门限。即此时门限值根据信噪比系数而变化。当信噪比较低时，提高判决门限；信噪比较高时，降低判决门限，以此减少落入不可信区间的概率，从而提高检测性能。其具体公式如下所示:

（3）每个认知用户根据式（12）对授权用户的信号进行能量检测，其中L代表采样点数，Xi代表每个认知用户接收的信号。然后将收集到的能量T和两个动态门限作比较。若高于λHi，则判定有主用户存在；若低于λLi，则判定为信道空闲，可供感知用户暂时接入，高低门限值根据信噪比系数自适应调整。当虚警概率一定时，可得检测概率如式（13）所示：

(4)在所有感知用户完成检测后，根据 “或”融合准则进行最终的判决。具有N个认知用户的判决过程如图3 所示。

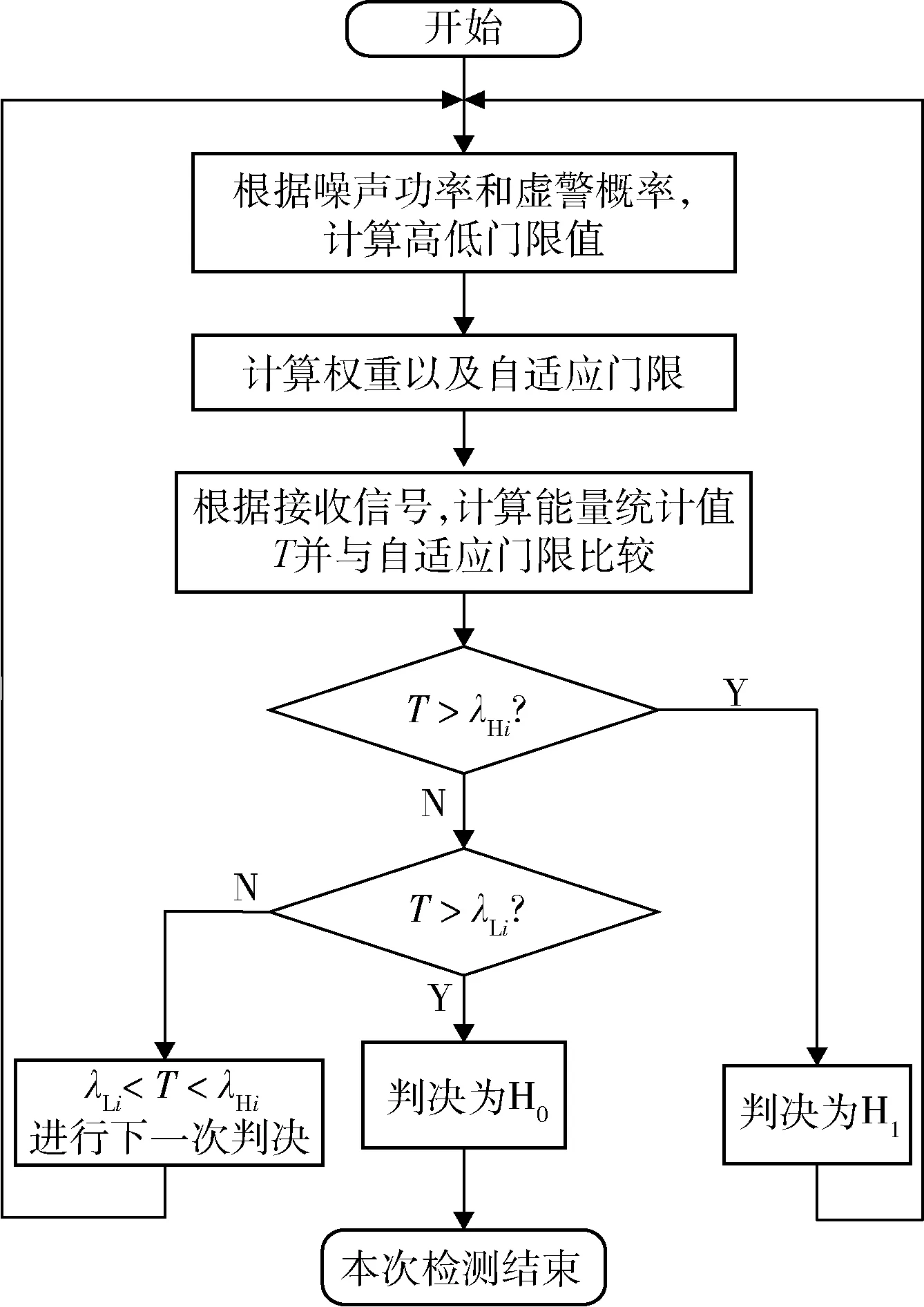
图3 算法判决流程图

3 仿真实验

3.1 不同信噪比下性能分析

首先设定本次实验具体相关参数，如表1 所示。

表1 算法主要参数

从图4 仿真结果可以看出，当感知用户N=2 且在信噪比为−2 dB 时，所研究算法的检测概率已经接近1。相比于传统的双阈值协作算法，要在信噪比为0 dB 时才接近于1；在信噪比为−8 dB 时，其他两种算法的检测概率远远低于本文所研究算法。因此，本文所研究的算法利用各个感知用户的信噪比，使得判决门限随信噪比系数自适应调整，在信噪比较低时其检测性能优于两种传统算法。

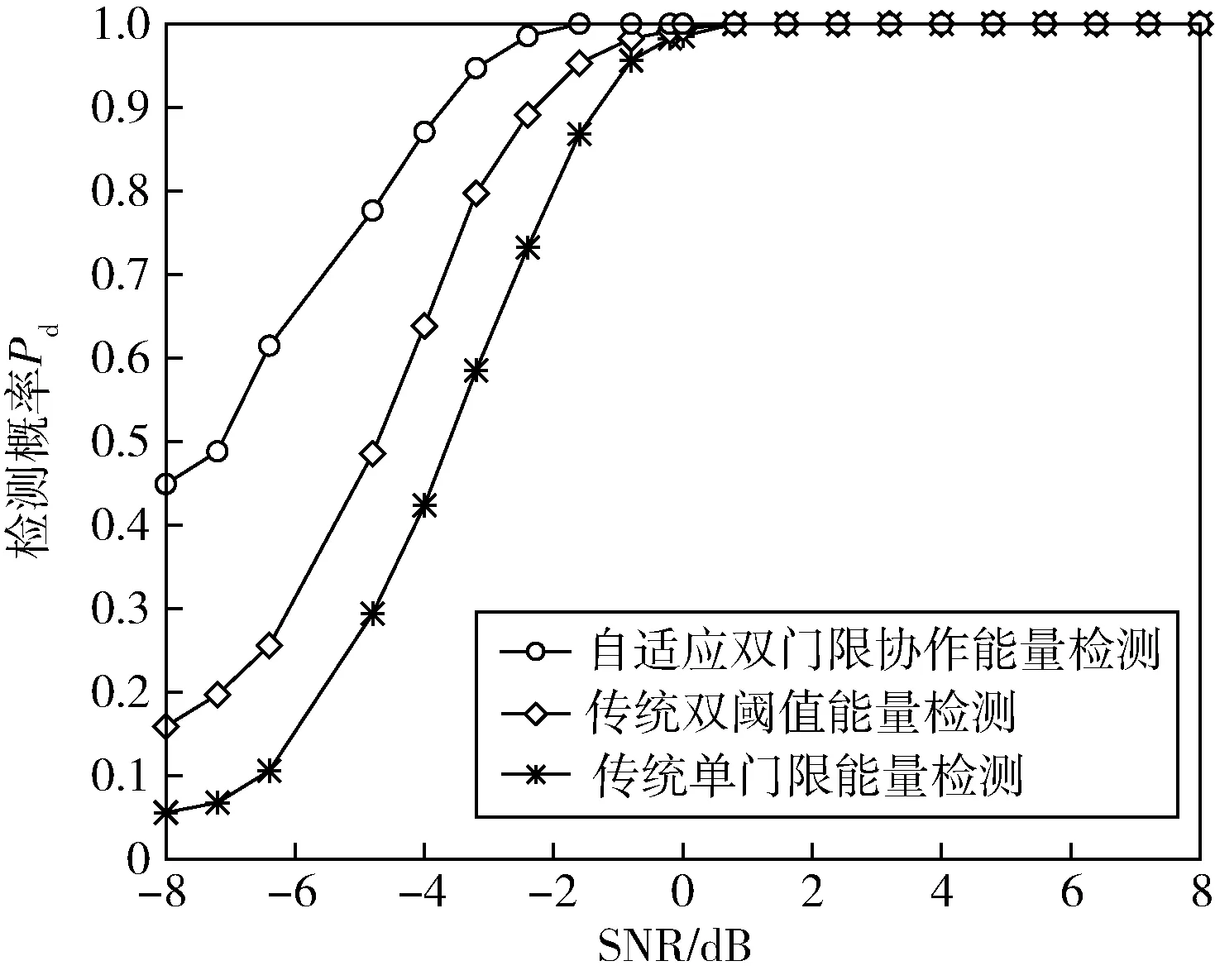
图4 检测概率分布图（感知用户N=2）

图5 是在图4 的基础上，在原有基础上增加了两个感知用户。从仿真图可以看出，在相同条件下，随着认知用户数量的增加，其检测概率得到了明显的提高。这是因为多用户共同感知时会产生协作增益，使得检测概率在原有基础上明显提高。根据前述的分析，可选择分布式协作的方式，并且将每个用户收集到的信息采用“或”融合准则进行判决，可以有效减少环境带来的不利影响，从而提高系统的检测概率。

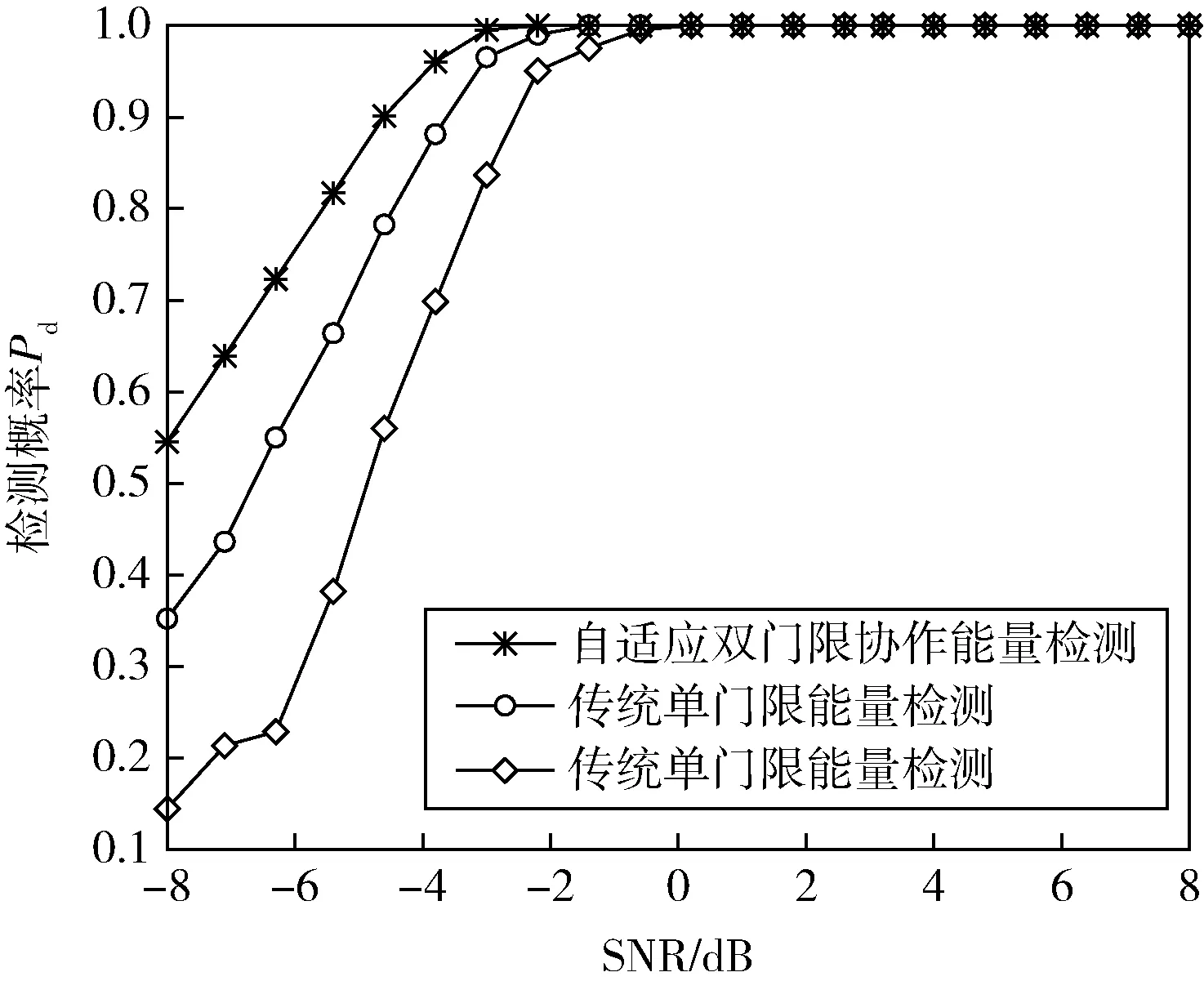
图5 检测概率分布图（感知用户N=4）

3.2 不同感知用户数性能分析

在实际的信道传输中，考虑到接收端容易受到多径衰落、阴影效应的影响，在信噪比分别为−4 dB 和−2 dB时加入了不同的感知用户数。其仿真结果如图6 和图7所示。

图6 检测概率分布图（SNR=−4 dB）

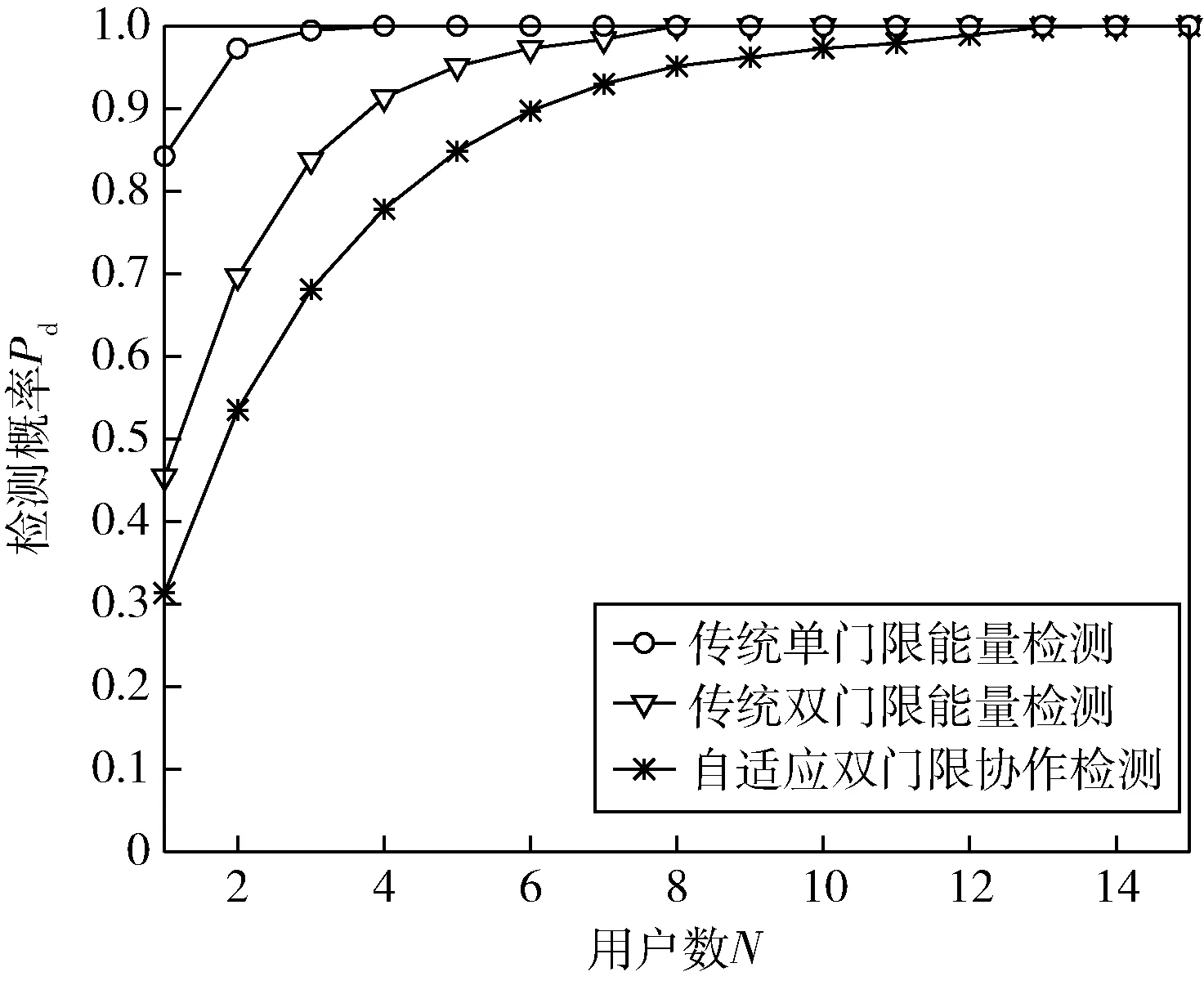
图7 检测概率分布图（SNR=−2 dB）

图6 和图7 表示了不同信噪比下各算法的检测概率随认知用户数量的变化。从仿真结果可以看出，本节所研究算法的ROC 曲线始终处于两种传统算法的上方。同时随着信噪比越高，所需要的认知用户数量也越少，在信噪比为−4 dB 时，本文所研究算法需要5 个认知用户，其检测概率可以趋近于1，当信噪比为−2 dB 时，本文所研究算法只需要3 个认知用户，其检测概率便可接近于1。综上，本文所研究的算法可在较低信噪比和较少认知用户数量的条件下，具有更高的检测概率。

3.3 不同虚警概率性能分析

为了从不同角度体现所研究算法的优势，在信噪比为−4 dB 时，虚警概率是10−4～10−2，感知用户个数N=5，其检测概率、漏检概率随虚警概率变化分别如图8、图9所示。其他实验参数与上述实验大致相同。

图8 虚警概率随检测概率变化图

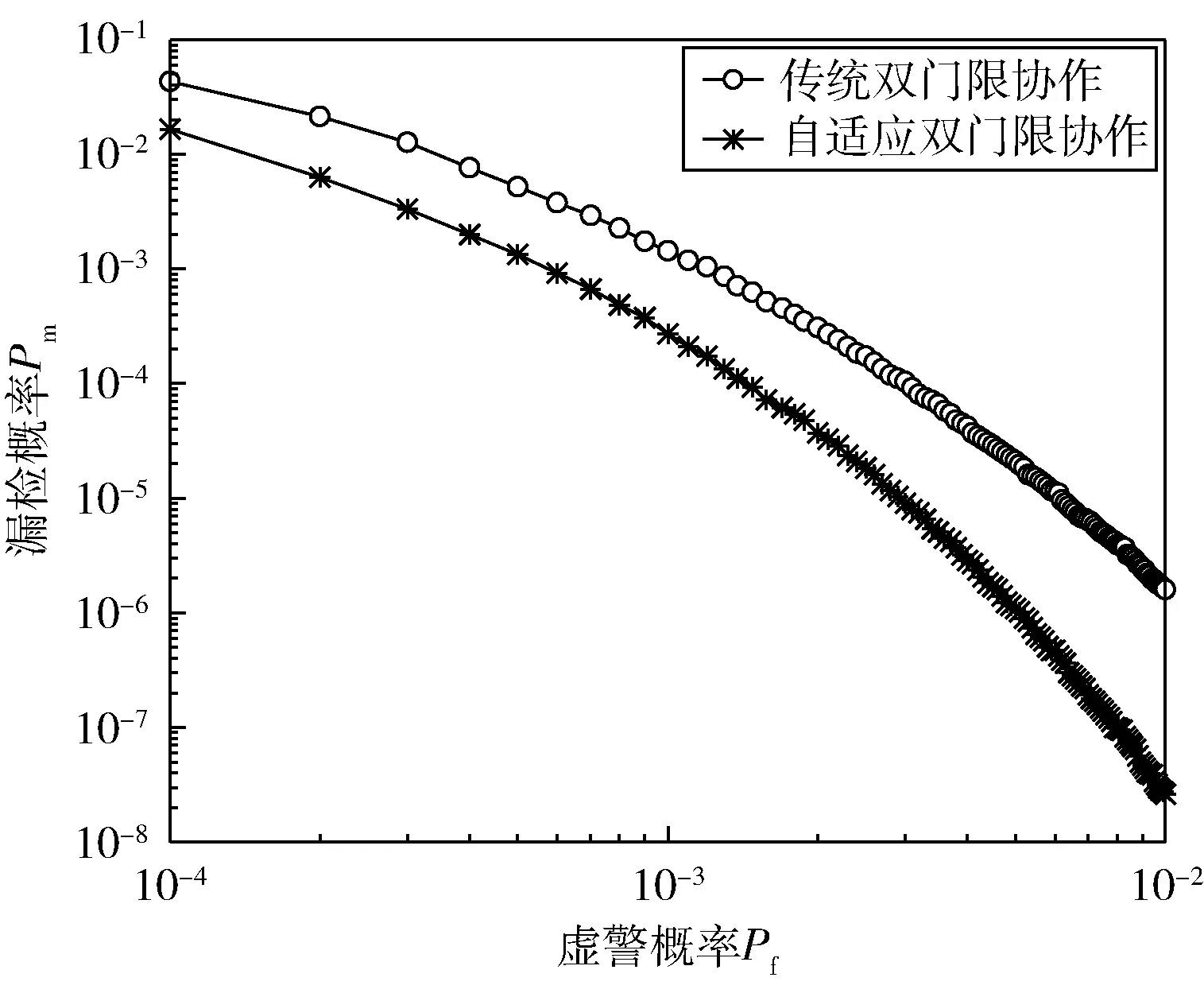
图9 漏检概率随虚警概率的变化曲线

图8 是在加性高斯白噪声信道中自适应协作算法与传统协作算法的ROC 曲线。通过仿真可以发现，虽然两种算法最终的检测概率都趋近于1，但是在虚警概率10−4～10−3之间本节所研究算法的ROC 曲 线始终在传统的双门限协作算法的上方，也就是说在检测概率一定时（假设Pd=0.99 时），本文算法的虚警概率低于传统的双阈值协作检测；在虚警概率一定时，本文算法的检测概率又高于传统的双阈值检测。

4 结论

传统能量检测算法在低信噪比检测概率效果不佳，这是由于判决阈值固定不变所导致的。基于以上传统算法的不足，本文研究了一种基于信噪比系数的双门限分布式协作的能量检测算法，使得判决门限随信噪比系数自适应变化。通过在不同信噪比、不同认知用户个数N以及不同虚警概率的情况下进行性能比较，所研究算法在低信噪比时具有更优的检测概率。然而，所研究算法在理想信道下进行使得检测结果存在着一定的局限性，由于在实际环境中系统中的噪声是无时无刻都处于变换的，因此可将该算法通过软件无线电平台放在真实通信环境中进行研究，使其具有更高的实用价值。