一种基于曲率和B 样条的矿区装载车辆连续路径规划方法①

禹鑫燚 刘逸哲 欧林林

(浙江工业大学信息工程学院 杭州310023)

矿山工作环境恶劣、危险程度高,矿山智能化是当前采矿行业发展的重要趋势。目前,国内部分矿山已经建成了自动化、信息化的采矿系统。装载车辆的自动驾驶是矿业智能化的重要组成部分。采用装载车辆自动驾驶技术可以有效减少对驾驶人员健康和安全的威胁,并大幅度提高生产效率、降低生产成本,并减少事故发生的概率。

路径规划技术是装载车辆自动驾驶技术研究的关键。传统的路径规划算法包括A∗算法[1-2]、人工势场法[3]和快速扩展随机树(rapidly-exploring random trees,RRT)算法[4]等。这些算法通常假设车辆是能够以任意方向运动的质点,并不考虑车辆的运动学模型,因此获得的路径通常难以执行。同时这类算法获得的路径大多数是离散点,需要和其他方法结合才能生成连续路径。因此,许多研究人员通过将路径规划与车辆运动学模型相结合的方式,优化现有的传统路径规划方法。Dubins[5]基于四轮车辆的运动学模型并假设车辆只能向前行驶,提出了Dubins 曲线,利用圆弧和线段获得了在满足曲率约束和规定的始端和末端切线方向条件下的最短路径。Reeds 和Shepp[6]在此基础上提出了Reeds-Shepp 路径,允许车辆在执行路径规划的时候执行后退的动作。Fraichard 和Scheuer[7]继续对该类型的路径进行优化,在线段和圆弧段之间插入了一段曲线,保证了曲率的连续变化。Dmitri 等人[8]将Reeds-Shepp 路径和A∗算法相结合,提出了混合A∗算法。混合A∗规划的路径考虑了车辆的运动学约束,使得A∗算法满足了车辆的最大曲率约束。这些方法保证了生成路径的连续性,同时也保证了车辆的运动学约束。为了获得更平滑的路径,一些路径规划方法引入了曲线插值方法,如多项式曲线[9]、回旋曲线[10]、贝塞尔曲线[11]和B 样条[12]。李玄赫[13]提出回旋曲线-圆弧-直线的路径规划方法,解决了车辆在窄车位的情况下自动泊车的问题。钱东海等人[14]利用三次B 样条曲线确定了满足自动导向车(automated guided vehicle,AGV)运动学约束的最短路径,使AGV 能够从偏移位置回到规划的连续路径上。Wu 等人[15]将B 样条和人工势场算法相结合,利用B 样条曲线对路径进行平滑处理,获得了较好的结果。Zeng 等人[16]讨论了B 样条控制点夹角对路径曲率的影响,并将其与RRT 算法相结合,使得车辆变道时可以实时生成连续路径。Mohamed 等人[17]利用B 样条实现了一种具有连续转向运动路径的算法,保证了生成的路径符合类汽车移动机器人的运动学约束。矿区装载车辆,在进入装载点前,车辆需要在回转点改变行进方向,以便倒车进入装载点。鲍久胜等人[18]利用改进A∗算法和人工势场算法对无轨胶轮车在井下执行任务进行路径规划,并利用三次样条插值方法进行路径平滑。在目前研究中,针对矿区环境下满足上述特殊任务的路径规划问题还未得到很好的解决。

本文针对矿区装载车辆在矿区工作过程中自动驾驶的路径规划问题,提出了一种新的路径规划方法。首先根据车辆的运动学模型,提出了一种基于曲率优化的A∗算法,获得符合车辆动态运行特性的离散路径。为了进一步求取连续的路径,基于车辆在初始位置和终点的位姿,提出了一种改进的B样条曲线插值方法,保证了路径两端的车辆方向。另外,为了确定车辆的回转点,利用模拟退火算法,结合初始路径,获得合适的回转点位置。最后,仿真实验证明了算法的有效性。该方法能够生成无碰撞的连续曲率路径,且保证了在路径两端的切线符合车辆的起止位姿。同时还可以有效找到一个回转点,使得车辆可以在回转点改变行进方向。

1 问题描述

矿场内装载车辆的基本功能是从矿场入口处驶入工作区域,然后在装载点进行装载,装载完毕后从离去点离开矿场,其工作示意图如图1 所示。

图1 装载车辆矿区工作示意图

在一般情况下,装载车辆需倒车驶入装载区,装载车辆必须在进入装载区之前改变方向。因此,需要找到一个回转点,使得车辆可以在回转点使运动方式从前进改为倒车。本文要解决的主要问题是,获得装载车辆的连续路径,使其满足以下2 个条件:(1)确定车辆出发点和离去点之间的路径,该路径需要连续且能避开环境障碍;(2)确定装载车辆的回转点,使得车辆可以在回转点处改变行进方向。

2 基于曲率和B 样条的连续路径规划设计方法

本文提出的装载车辆路径规划方法主要包括基于曲率优化的A∗算法设计、两端导数约束的B 样条连续路径获取以及回转点确定。基于装载车辆的运动学模型设计成本函数,对A∗算法进行改进,获取装载车辆从出发点到装载点的离散路径点的运动路径,进一步,将利用两端导数约束的B 样条路径进行路径插值,然后利用改进B 样条插值求出连续路径,之后在求出连续路径的情况下利用模拟退火算法求出回转点。最后利用A∗算法和改进B 样条求出各点之间的连续路径。

2.1 基于曲率优化的改进A∗算法

A∗算法是一种启发式的路径规划算法,常用于解决静态路网求取最短路径的问题。相对于Dijkstra 算法,A∗算法加入了启发信息进行搜索方向引导,提高了路径搜索效率。A∗算法的成本公式为

其中,f(n) 为A∗算法的路径成本,g(n) 为初始位置到位置n所需的最小路径成本,h(n) 为位置n到最终位置的估计路径成本。常见的A∗算法中,2点间路径成本通常定义为2 点间的欧氏距离,即2点之间的直线距离。为了使得装载车辆能够准确跟踪所生成的路径,本文基于装载车辆运动路径的曲率对成本函数式(1)进行了设计。

考虑如图2 所示的装载车辆运动模型,车辆只有前轮可以转弯。其中,(x,y) 为车辆的位置,定义为车辆后轮的中心;θ为车辆相对于x轴的方向;ρ为车辆转弯半径;L为车辆的轴距长度;ϕ为车辆的转向角。

图2 车辆运动模型

定义曲率κ为车辆转弯半径的倒数,可得:

对式(2)进行微分,可得:

当ϕ足够小的时候,可以认为tanϕ≈ϕ,cosϕ≈1,因此式(3)可以近似为

在路径规划过程中,希望路径的曲率不发生过大的变化,因此根据式(4),定义如下的路径成本函数,其中ω1和ω2为大于0 的常数参量。

其中,θi为路径中的第i个点所对应的车辆位姿,Δsi为第i段路径。根据中心差分的前向差分公式和后向差分公式,可求得前向差分公式为

在点n处的后向差分公式为

将式(10)作为路径曲率成本应用于A∗算法中,代替原来的路径距离成本,可以得到初始位姿到点n的已知路径曲率成本g(n) 和点n到终点位姿的路径曲率成本h(n)。假设点k为目标点,则可以得出A∗算法中的路径成本公式需修改为

式(11)显示,在本文中,路径成本即为路径的曲率成本。其中g(n) 为起始点到当前探索节点n的最小路径曲率成本,h(n) 为当前探索节点n到最终位置k的预估路径曲率成本。

2.2 两端导数约束的B 样条路径

2.1 节中利用改进A∗算法求取了车辆的运动路径,并获得了车辆运动路径的离散点,在本节中,将利用两端导数约束的B 样条进行路径插值,获得连续路径。

一般情况下,p次B 样条通常写成如下形式:

其中,Pi为对应控制点;Ni,p(u)为p次基样条;r(u) 为对应值的B 样条曲线上的插值点,m为生成B 样条所需的控制点数目;u为B 样条基样条求取的插值参数,u∈[0,1)。由于生成的路径要保持曲率连续,因此需要生成的B 样条保证C2 连续,即生成曲线的二次导数为连续,故至少要使用三次B 样条,因此p取值为3。假设所生成的离散路径点数目为n,且生成的B 样条函数必须经过两端点,则根据非均匀有理B 样条的基本性质,所需控制点数目为m=n+p +1=n +4。

根据式(12),为了获得B 样条曲线,需要获得B 样条的基样条。利用De-Boor 递推式可以获得任意阶数的B 样条基函数。De-Boor 递推式为[20]

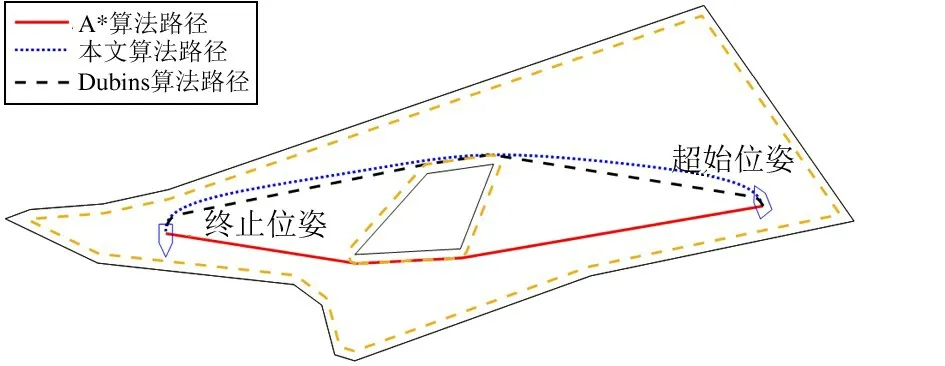
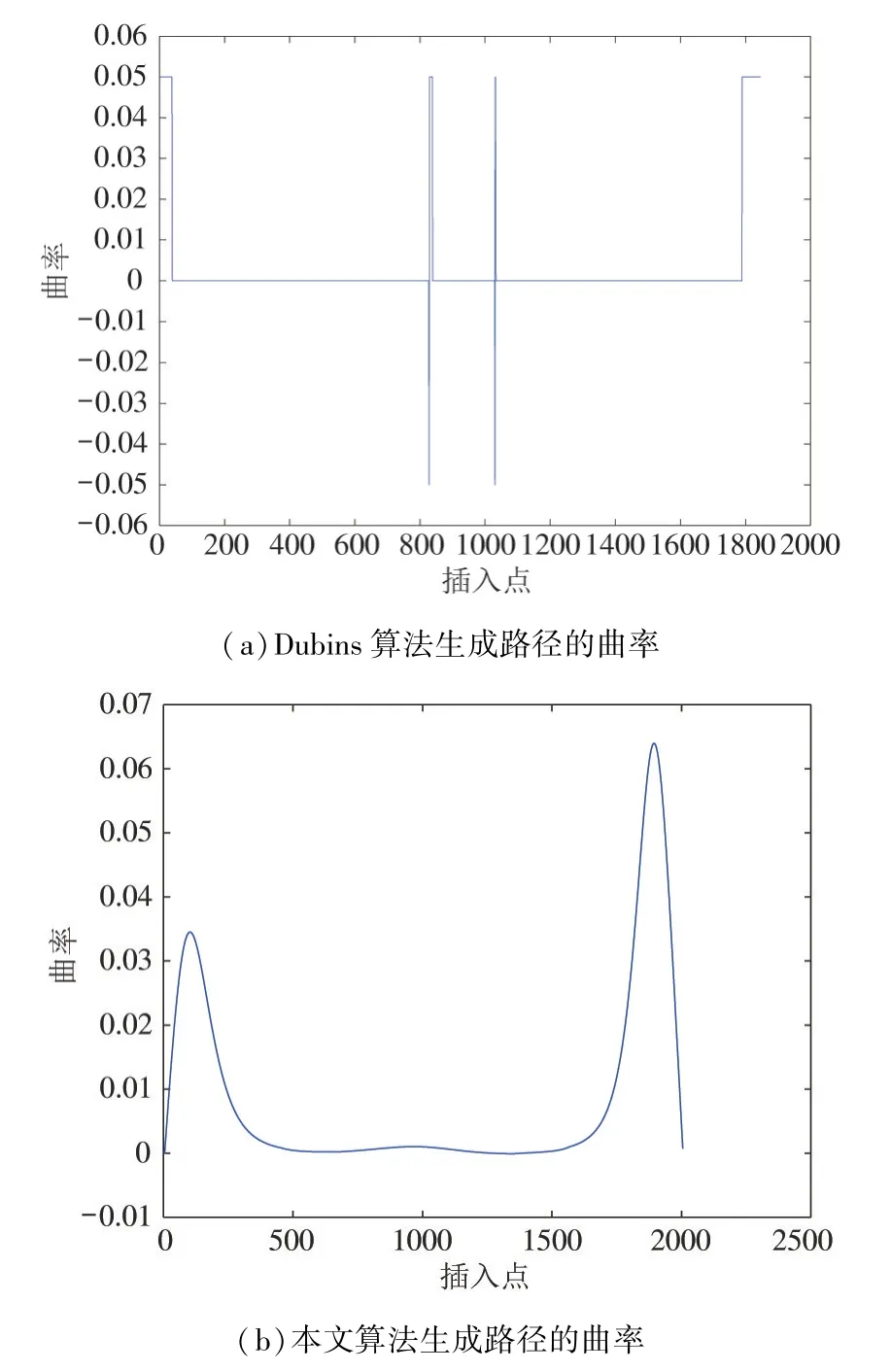
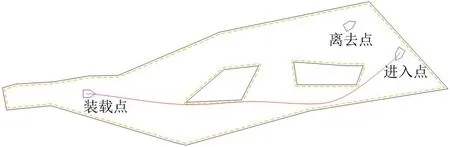
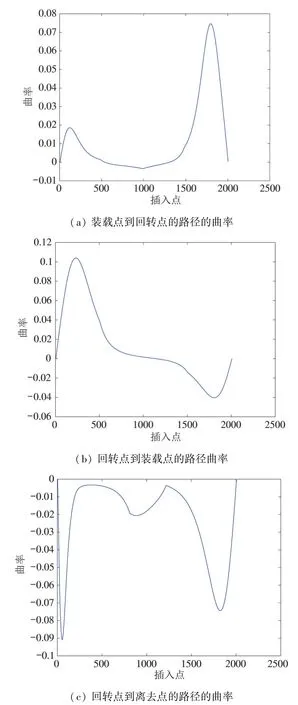
其中,ui为节点,且ui

假定数据点Qi为根据改进A∗算法获得的路径点。首先,根据弦长法,将弦长参数τi赋给每一个数据点Qi:

其中,d为整段路径的距离,n为路径点数目。在获得弦长参数τi后,定义出实数序列U中的节点ui。根据NURBS 的定义[20],为了获得三次B 样条,需要在B 样条的起点和终点处重复4 次节点。因此实数序列U可以定义为

其中,m为生成实数序列中的节点数目,τi为弦长参数中第i个弦长。

常规的B 样条曲线并没有考虑曲线两端的导数约束,因此生成的路径并不能反映车辆的真实运动轨迹。因此需要在B 样条两端考虑车辆位姿的约束,使得生成的轨迹符合车辆的运动轨迹。假设车辆在路径两端都是无转向动作的,因此可以在轨迹两端用导数来表示车辆位姿约束。

将路径两端车辆运动方向表示为向量D0和Dn。在2 个端点处的车辆方向向量由B 样条导数决定。对于实际路径,车辆在进入点和离开点都为直线运动,不存在转弯,因此在这2 个点上车辆的曲率为0。对于任意曲线上的一点,其曲率公式被定义为

其中y为曲线上对应点的具体数值。因此在该点上的B 样条曲线二次导数为0。为此,需要求取B 样条2 端点处的一次导数和二次导数。B 样条导数公式为

其中,j为导数次数,m为控制点数目,r(j)(u) 为B样条对应插值点上的j次导数值,(u) 为基样条的j次导函数,Pi为B 样条控制点,u为B 样条基样条的求取插值参数且u∈[0,1)。基样条的j次导函数(u) 的求取公式为

其中p、j、u的含义同式(17)一致,ui为对应的实数序列中第i个节点。通常情况下,LU 分解被用来求取B 样条的控制点[20],可以将起始点和终点的导数约束写入求取控制点的公式中,改进B 样条求取控制点的公式如式(19)所示。在式(19)中,为了获得最优的B 样条路径,需要优化参数α和β。

由于生成B 样条时需要考虑生成路径的曲率,同时希望生成路径的曲率的变化率不要过大,故B样条的成本公式需要考虑曲率对路径的积分以及曲率对路径导数对路径的积分。因此,定义如下的B样条成本公式:

其中κ为曲率,ω1和ω2为大于0 的常数参量。根据式(15),可以定义出B 样条上任意一点的曲率公式和曲率导数公式如式(21)和(22)所示。

利用高斯-勒让德积分公式对式(20)进行评估,并利用Powell 方法对评估后的公式做最小化处理,可以获得α和β的值。

在求取完B 样条后,需要对B 样条中的插值点进行检测,以防止车辆路径和障碍物发生碰撞。首先,对障碍物进行Minkowski 和扩展,得到膨胀区域,定义当路径点经过膨胀区域内,就认为车辆在该点处和障碍物发生碰撞。随后从B 样条初始位置的点开始每隔10 个采样点就选取1 个采样点进行检测,当发现在该点处车辆会和障碍物发生碰撞之时,将该点沿法线方向移动一个车辆轴距,如果仍旧发生碰撞,则继续向外移动,直至该点不和障碍物发生碰撞。为了简化计算,定义B 样条路径上的采样点的法线的方向为pi到pi-10的向量与pi到pi+10的向量之和的方向,其中pi为B 样条上第i个采样点。之后,将该点作为新的中间点加入离散路径。在加入离散路径后对该点进行优化。以中间点为圆心绘制2 个圆,圆半径分别为3/4 轴距和1/2 轴距。在2 圆上分别以等圆心角取8 个点,根据式(11)计算每个点的成本,并将其移动到成本最小的定位点上。然后重新以其点作为圆心重复上述步骤。B 样条连续路径生成的流程图如图3 所示。车辆从起始点到终点生成连续路径的路径规划整体算法如算法1所示。

图3 B 样条连续路径生成流程图

2.3 回转点的求取

一般情况下,装载车辆会以后退的方式进入装载区,因此,它必须在进入装载区之前在回转点改变方向。车辆在回转点前后的路径如图4 所示。

图4 车辆在回转点前后的路径

车辆回转点由3 个参数确定,分别为(x,y,θ),其中x、y为车辆的位置坐标,θ为车辆的姿态角度。回转点的成本根据下式进行计算:

其中Es→t为起始点到回转点的路径成本函数,Et→l为回转点到装载点的路径成本函数,ω1和ω2为大于0 的常数参量。路径成本函数由式(11)估算决定。在理想情况下,回转点应当尽量不偏离原路径,因此基于2.3 节中所得到的连续路径寻找装载点。如图5 所示,从装载点处回溯长度为b的距离,然后将这个点沿垂直于曲线凸边的向量移动长度为a的距离,将移动之后的点确定为回转点。将回转点的方向确定为垂直于曲线凸边的向量的方向。

图5 回转点的确定

模拟退火算法模仿了玻璃退火的物理过程,相较于贪心算法,其具有一定概率跳出局部最优解,可以有效求出整体最优解。因此,本文中利用模拟退火算法[21]来获得最优的外移距离a和回溯距离b。首先确定初始迭代值。本文中,规定初始回溯距离b等于5 倍车辆轴距长度,外移距离a等于车辆轴距长度。随后对回溯距离b和外移距离a进行随机扰动,即:

为了防止回转点偏离装载点太远,在本文中,规定amax为5 倍车辆轴距,bmax为10 倍车辆轴距,都要进行距离检测和碰撞检测。当发现回溯距离b大于整体线段长度或者在该组数据下生成的点可能发生碰撞,则将该组数据作为无效数据舍弃,该次迭代的数据仍为原数据。

根据模拟退火算法,当在一个温度下执行固定次数迭代或达到平衡时,在该温度下的熔化过程停止,降低温度后继续进行迭代,直至温度小于最低温度,停止迭代。式(25)给出了降温的过程。

其中Ti为第i次迭代所到达的温度。

相较于典型的寻找回转点的方法[17],本文所提出的方法仅需寻找2 个参数,而不是直接寻找回转点(x,y,θ),使得生成点可以直接插入离散路径中,不必在每一次进行成本估计的时候先进行路径搜索再预估成本,有效降低了模拟退火算法循环过程中的单次运行的时间。在单次循环中,三参数模拟退火算法的复杂度为Ο(n3),而本文算法中单次循环复杂度为Ο(n)。

矿区车辆在执行装载任务过程中的整体路径规划的算法如算法2 所示。

3 仿真

为了验证路径规划的有效性,本文对所提出的装载车辆路径规划方法进行了验证。假设装载车辆从进入点进入矿场,前往装载点进行装载,装载完毕后从离去点离开矿场。由于车辆进入装载点进行装载时需要倒车进入,因此需要在进入装载点之前改变车辆的行进方向。因此,路径规划算法的主要任务是:(1)找到两点之间的曲率连续的无碰撞路径;(2)找到一个回转点使得车辆可以调转行驶方向。

3.1 路径规划算法的对比

实验1 选取了A∗算法和Dubins 算法与本文提出的路径规划算法进行对比。这是2 种典型的路径规划算法,在路径规划过程中有广泛的应用。将模型导入仿真软件,并确定车辆的起止位姿。其中地图尺寸为1 300 ×450,车辆起始位姿为(1 105,206,120 °),3 个参数分别代表车辆位置(x,y)和车辆姿态角θ。车辆的终止位姿为(306,205,-90 °)。随后分别利用A∗算法、Dubins 算法和本文所提出的算法进行对比,生成的路径如图6 所示。其中实线为A∗算法生成的路径,点线为本文算法生成的路径,虚线为Dubins 算法生成的路径。

图6 3 种路径规划算法的对比

由于无需进行路径平滑插值,A∗算法所花费的时间最少,但是A∗算法生成的路径为离散折线路径,且生成的路径并不符合车辆在起始点和终点的位姿。Dubins 算法和本文算法都可以生成连续路径,且生成的路径符合车辆在起点和终点的位姿。同时,Dubins 算法生成连续路径的时间为0.334 19 s,本文算法生成连续路径的时间为0.379 32 s,可见本文算法和Dubins 算法在计算时间上没有明显的差距。为此,本文对比了本文算法和Dubins 算法生成路径的曲率变化,2 种算法生成的连续路径的曲率变化图如图7 所示。

图7 Dubins 算法和本文算法生成路径的曲率对比

由图7 可见,Dubins 曲线生成的路径会在圆弧和直线的交接处发生曲率突变的现象,且在起始位姿和终止位姿处曲率皆不为0,而本文所生成的路径曲率连续变化,不会发生突变现象,且在起始位姿和终止位姿处的曲率皆为0,减少了车辆的轮胎磨损。

3.2 矿区全流程连续路径获取

实验2 利用障碍物较为稀疏的情况来演示算法的全流程。

首先,将矿场数据和障碍物数据导入仿真软件中,地图尺寸为1 300 ×450。并设置车辆的进入点位姿,装载点位姿和离去点位姿。车辆进入点位姿为(1 206,285.5,-120°),车辆装载点位姿为(306,276,0 °),车辆离去点位姿为(1 056,354,30 °)。矿场地图如图8 所示,其中黑色表示矿场边界和障碍物,虚线边框为利用Minkowski 和生成的膨胀区域边界。当点位于膨胀边界当中时,可以视为车辆和障碍物发生碰撞。

图8 矿场地图

随后,利用2.2 节提出的改进A∗算法和2.3节提出的B 样条1 插值法生成车辆从进入点到装载点的路径,如图9 所示。需要注意的是,在生成该路径时,为了方便之后回转点的求取,默认车辆在装载点的朝向为车辆在装载点位姿的反方向。

图9 车辆从进入点到装载点的B 样条路径

然后,利用2.4 节的方法获得回转点,并利用改进A∗算法和B 样条获得装载车辆全流程的路径。生成的全流程连续路径,如图10 所示。可见该算法可以生成无碰撞路径且能找到一个回转点,能够较好地完成任务。需要注意的是,由于车辆是从回转点倒车进入装载点,因此在求取回转点到装载点路径的时候算法输入的位姿方向为两点处的车辆位姿的反向。

图10 全流程连续路径

同时进行了2 种回转点搜索算法搜寻回转点的对比,2 种算法都可以较好地搜索出如图10 所示的回转点,但是文献[17]的三参数模拟退火算法单次搜索时间明显长于本文的算法,本文算法单次循环平均时间为0.02 s 左右,而文献中所示的模拟退火算法单次循环的平均时间在9.8 s 左右。

实验2 所生成路径的曲率如图11 所示。由图11可见,本文提出的算法所生成的路径为曲率连续变化的曲线,且在起始点和终点处的曲率为0,而Dubins 曲线在圆弧和直线相交的部位会出现曲率突变的现象,且在生成的路径两端曲率为最大。因此本文所提出的路径可以较好地完成装载车辆的路径规划任务。

图11 三段连续路径曲率变化

3.3 密集障碍物情况下的连续路径规划

实验3 考虑障碍物较为密集的情况。将矿区边界数据和障碍物数据导入仿真软件,地图尺寸为700 ×350。其中,车辆初始点位姿为(106,204,-15 °),车辆装载点位姿为(405,96.3,90 °),车辆离去点位姿为(506,193.6,-30 °)。在障碍物密集的情况下,所获得的全流程连续路径如图12 所示,生成的3 段连续路径的曲率变化如图13 所示。仿真结果表明,即使障碍物之间存在间隔较窄的瓶颈区或者装载点附近较为狭窄的情况下也可以规划出全流程路径,且曲率变化连续。

图12 障碍物较为密集的情况下的全流程路径

图13 三段连续路径的曲率变化

4 结论

本文针对矿区环境下装载车辆的路径规划问题进行了研究,设计了一种基于曲率和B 样条的路径规划算法。基于车辆的运动学模型改进了A∗算法的成本函数,保证了生成的离散路径更接近车辆可执行的最优离散路径。基于此离散路径,通过改进三次B 样条曲线规划出装载车辆的连续路径,保证了生成路径两端的切线方向符合车辆的位姿。并考虑装载车辆的任务特点,基于模拟退火算法确定了装载车辆在矿场中的回转点位置。仿真实验结果表明,本文提出的连续路径规划方法可以规划出质量较高的曲率连续路径,且能求出合理的回转点,并且在障碍物较为密集的情况下依然有效,因此本文所提出的连续路径规划方法可以有效地为自动驾驶装载车辆提供曲率连续的无碰撞路径。