基于持续强化学习的自动驾驶赛车决策算法研究①

牛京玉 胡瑜 李玮 韩银和

(∗中国科学院计算技术研究所智能计算机研究中心 北京100190)

(∗∗中国科学院大学 北京100049)

自动驾驶赛车挑战赛[1-4]的兴起反映出自动驾驶赛车已成为当下促进高速自动驾驶技术发展的一个研究热点。最近的研究进展表明,深度强化学习(deep reinforcement learning,DRL)[5]是解决自动驾驶赛车决策问题的一个潜力研究方向[6-7]。DRL 通过试错方式自主学习最优驾驶策略,令赛车在动力学模型固定的道路上实现累计奖励的最大化。这里的动力学模型由道路形状以及摩擦系数、滚动阻力系数、粗糙度等路面物理参数信息共同描述。动力学模型不同的道路被视为不同任务。当道路的形状或路面参数发生变化时,传统DRL 策略会在继续学习新任务时遗忘旧任务,即发生灾难性遗忘,从而无法应对道路多变的实际赛车需求,比如拉力赛[8]。为此,针对赛道涵盖多种道路形状和材质的情况,本文开展面向多任务的持续强化学习[2-10](continual reinforcement learning,CRL)自动驾驶赛车决策算法研究。

CRL 的核心定义是策略在不断学习新任务的过程中不遗忘旧任务知识,即无灾难性遗忘。其还有2 个进阶能力:积极前向迁移和后向迁移。前者指策略利用旧任务知识帮助新任务更快或更好收敛的能力。后者指策略利用新任务知识反过来帮助提高旧任务表现的能力。可见,无灾难性遗忘就是积极后向迁移的下限。

现有相关CRL 工作可分为3 类:经验回放方法[11-17]、参数独立方法[18-19]和权重正则化方法[20-23]。然而,前2 类方法是通过持续保存旧任务数据或扩张策略网络规模来实现CRL,存在数据存储压力大、可扩展性差的缺点,难以满足复杂自动驾驶任务的长期决策需求。第3 类权重正则化方法计算策略网络权重对各个旧任务的重要性,并限制对旧任务重要的权重在新任务学习期间的更新。该类方法能在无需存储旧任务数据或扩张网络规模的条件下令强化学习(reinforcement learning,RL)策略避免灾难性遗忘,可满足自动驾驶应用需求。但权重正则化方法对所有旧任务施加了无差别的权重约束,忽略了任务之间的相似性关系,导致其持续学习能力受限。另外,这些方法还存在2 点不足:未充分利用RL 的优化要素来提升持续学习效果,以及未应用于复杂的高速驾驶任务中。

为克服上述缺点,本文提出一种融入任务相似性的两阶段CRL 算法框架。其中包含4 个主要创新点。(1)算法第1 训练阶段提出了一种无监督的任务特征提取方法。该方法包含1 个特征提取器和1个动力学权重生成器。两者的联合训练可获取描述任务动力学特征的低维向量。这些任务特征用于计算任务相似性关系。(2)算法第2 阶段提出了一种融入任务相似性的权重正则化方法。该方法利用任务相似性关系来自适应地调节策略网络权重的更新约束。当新旧任务相似性低时,加强限制对旧任务重要的部分权重发生变化。反之,减弱对权重更新的限制,以提供任务间进行知识迁移的机会,获得进阶CRL 能力。(3)算法第2 阶段还设计了一个适用于持续学习的RL 奖励函数,促使策略向着共同提高新任务和旧任务性能的方向优化。(4)本文利用赛车仿真平台设置了一系列测试实验,定义了一套评估CRL 方法的性能指标。实验结果表明,在不存储旧任务数据且不扩张策略网络规模的条件下,本文算法能获得比所有基准CRL 方法更亮眼的成绩。

1 相关工作

持续学习已经在监督学习领域,尤其是在图像分类任务中获得了较深入的研究[24-26]。最近,RL中的持续学习问题[9-10]也受到了越来越多的关注。相关CRL 方法主要可分为经验回放方法、参数独立方法和权重正则化方法。

经验回放方法实现CRL 能力的思路是存储旧任务数据,并用其与新任务数据一起优化策略。其中一部分方法关注如何在维持无灾难性遗忘的同时缓解数据存储压力,比如利用不同数据抽样方法精简存储[11-13]或学习数据生成模型[14-15]。该类别中的另一部分方法关注如何获取进阶CRL 能力。比如梯度情景记忆(gradient episodic memory,GEM)方法[16]和平均梯度情景记忆(averaged GEM,A-GEM)方法[17]约束策略在新任务上的梯度更新方向与在旧任务上的梯度方向间夹角不超过90 °,从而与新任务相似的旧任务能在新任务学习中获得积极的后向迁移。但随着任务数的增加,这类方法的数据存储压力加剧,不适合自动驾驶赛车应用的长期决策需求。

参数独立方法保留旧任务知识的思路是为每个任务扩展一部分独立的策略网络分支,其代表性方法是渐进神经网络(progressive neural networks,PNN)[18-19]。除了避免灾难性遗忘问题外,该方法还具备积极的前向迁移能力。其得益于PNN 中从旧任务网络到新任务网络的横向连接,令策略有选择地从相似旧任务网络中获取促进新任务收敛的有用知识。但策略网络分支彼此独立一方面导致无法发展后向迁移能力,另一方面导致网络规模随着任务数的增加而不断扩张,可扩展性差。该方法同样不满足自动驾驶赛车的应用需求。

权重正则化方法的思路是计算策略网络权重对每个旧任务的重要性,并在新任务训练时限制对旧任务重要的部分策略权重更新。其代表性方法是利用Fisher 信息矩阵估计重要性的可塑权重巩固(elastic weight consolidation,EWC)[20-21]。在线可塑权重巩固(online EWC)方法[22-23]降低了EWC 方法的计算成本。渐近压缩(progress &compress,P&C)方法[23]结合PNN、online EWC 和知识蒸馏思想提出一种可扩展策略。这类方法既无需存储旧任务数据也无需扩张网络规模,该优势使其适用于自动驾驶赛车的应用需求。但由于权重正则化方法对所有旧任务的无差别约束,这类方法仅局限于解决无灾难性遗忘问题。将权重正则化方法和可获取部分进阶CRL 能力的GEM、A-GEM 和PNN 方法相比较可以发现:可获得部分进阶CRL 能力的3 个方法的共性在于均隐含考虑了新旧任务间的关系。因此,本文提出一种融入任务相似性的权重正则化方法。该方法利用任务相似性对不同旧任务的约束力度进行自适应调节,从而实现积极前向和后向迁移能力。为计算任务相似性,本文提出一种特征提取方法来获取描述每个任务动力学特征的低维向量。此外,本文还设计了一个适应CRL 的奖励函数,以进一步发掘RL 优化范式下的持续学习能力。上述3 项创新设计共同构成了本文满足自动驾驶赛车需求的CRL 算法。

2 方法介绍

2.1 问题定义

本文旨在提出CRL 算法解决传统RL 策略面对道路变化时的灾难性遗忘问题。每段动力学表现不同的道路被看作一个独立任务。赛车在每个任务上的RL 决策过程均为一个由元组(S,A,P,r,γ) 表示的马尔科夫决策过程。其中,S是状态空间,A是动作空间,P是描述任务动力学的状态转移函数,r是引导RL 优化方向的奖励函数,γ是折扣因子。不同任务具有相同的状态空间、动作空间和折扣因子。任务间的差异体现在状态转移函数和奖励函数随任务变化。设i∈{1,2,…,T} 是任务标识,t是时间步,状态转移函数和奖励函数分别表达为Pi(st+1|st,at)和。第t时间步时,赛车状态st∈S是一个29 维多传感信息向量,包括赛车和道路轴线的夹角及距离、三维速度信息、赛车与道路边缘的19 维测距信息、4 个轮速转速和发动机转速。赛车动作at∈A表达为由转向、加速度组成的二维向量。

2.2 算法概述

当赛车遇到一个新任务i时,图1 展示了本文提出CRL 算法的2 个训练过程。第1 训练阶段旨在提取可描述当前任务动力学的低维特征向量featurei。该任务特征的提取利用了一个编码器E和一个权重生成器Gdyn的联合训练结构实现,过程详见2.3 节。学到的新任务特征被用于计算新任务与前i -1 个旧任务之间的相似性关系。第2 训练阶段旨在向着既学习新任务又不遗忘所有旧任务知识的方向优化当前策略。策略的CRL 能力由融入任务相似性的权重正则化方法以及鼓励持续学习的RL 奖励函数共同实现,详见2.4 节的介绍。

图1 本文两阶段CRL 算法的训练过程总览图

2.3 第1 训练阶段:提取任务特征

本文算法的第1 训练阶段展示在图1(a)中。首先,算法通过随机驾驶起点和控制动作的方式收集新任务环境i中的轨迹数据。这些数据包含了车辆和任务i道路之间的动力学关系。然后,从轨迹数据集中取时间间隔为k的数据喂进特征提取器中输出特征向量,即再将featurei作为任务i的动力学权重生成器的唯一输入,获得一组网络权重,即这些网络权重可导入不可学习的动力学模型中,并根据当前状态和当前动作预测智能体在当前任务i中获得的下一时间步状态,即本文采用一个动力学权重生成网络而不是动力学模型来辅助训练特征提取器的原因是:生成器把任务特征当作唯一输入,而动力学模型只将任务特征作为部分输入,前者能提供比后者更强有力的训练约束。

(1) 网络结构设计。以轨迹数据为输入的特征提取器采用了长短期记忆(long short-term memory,LSTM)结构[27],这是一种适合处理时序信息的循环神经网络。又因为轨迹数据中包含的状态信息有位姿、速度等非图像数据,所以动力学权重生成模型网络和动力学模型均采用全连接网络实现。通常,应对复杂控制的动力学模型包含多个神经网络层,且每层需要数百个神经元来获取足够的表达能力。大量模型权重直接从权重生成器输出会引发生成器网络规模和计算压力过大的问题。为了避免该问题,本文受文献[28]启发,设计了一个可利用少量网络参数实现复杂动力学的权重生成器结构。

(2)第1 训练阶段的损失函数。权重生成器的训练目标是从特征提取器输出的任务特征中获得一组精准的动力学模型权重。这促使特征提取器聚焦轨迹数据中的车辆-道路动力学信息。因此,特征提取器和权重发生器的网络通过最小化动力学损失函数优化。该损失函数计算了下一时间步状态真值和由动力学模型计算的下一时刻状态预测值之间的加权均方误差,如式(1)所示。

其中,M是每次训练采样数据的批尺寸(batch size),N是每个状态中包含的传感器类别个数,不同传感器信息的均方误差具有不同的加权参数bn,和分别代表着真实状态和预测状态中的第n个传感器信息。

此外,特征提取器E的优化还需要一项额外的损失函数LE来确保featurei对任务i来说是唯一的,如式(2)所示。

其中,每次针对任务i的训练需要采样2 个批尺寸均为M的轨迹数据批,为保证M/2 为整数,M设为偶数;和分别表示来自这2 个轨迹数据批中的第m个数据;q∈{1,2} 代表着这2 个轨迹数据批中的第q批数据。该损失函数约束了特征提取器从不同轨迹数据批中学到相同的任务特征。

2.4 第2 训练阶段:策略持续学习

图1(b)描述了本文算法的第2 训练阶段。本阶段对RL 优化损失进行了2 项持续学习设计。这里采用基于最大熵原理的软演员-评论家(soft actor critic,SAC)算法[29-30]作为本文的RL 实现基础。SAC 算法在最大化折扣奖励期望的同时最大化策略的熵H,如式(3)所示,令策略具备适应环境变化的鲁棒性。

其中,γ是折扣因子,π∗是学到的最优策略,重放缓冲器D用于存放赛车与当前环境的交互数据(st,at,st+1,rt),E(st,at)～D是求期望符号,α是影响最优策略随机性的温度因子。

在具体实现上述目标函数时,SAC 算法采用演员-评论家(actor-critic)结构,包括1 个策略网络(policy network)和2 个Q 值网络(Q-value function)。策略网络是根据当前状态st生成当前动作at的演员,即at=π(st)。2 个Q 值网络Q1(st,at)和Q2(st,at) 是评估生成策略质量的评论家。Q 值网络先利用累计折扣奖励值进行训练,再来指导策略网络的优化。由于SAC 算法有2 个Q 值函数,每次网络更新均采用两者的最小值参与计算。这种双值函数做法[31]缓解了由值函数过度估计偏见导致的策略性能下降。

需要注意的是,现有CRL 策略输入往往包含当前状态st和任务标识i的嵌入向量(embedding vector)2 部分信息。本文将任务特征featurei代替现有方法中使用的任务嵌入向量,即和

(1) 融入任务相似性的权重正则化损失。当学完任务i -1 后获得的最优策略遇到新任务i时,先从本文算法第1 训练阶段获得任务特征featurei。接着,该特征向量参与到策略网络πi在新任务i上的优化过程中。策略网络的损失函数如下所示。

其中,Ltaski代表原始SAC 策略损失项,如式(5)所示。其具体的推导细节可参考文献[30]。

式(5)中的Lregz是本文设计的融入任务相似性的权重正则化项,其表达如式(6)所示。

其中,超参数λ用于平衡Ltaski和Lregz对策略优化的影响程度;Simi c∈[-1,1] 表示新任务特征向量featurei和某一旧任务特征向量featurec(c∈{1,…,i-1}) 间的相似性;Fc指Fisher 信息矩阵,由刚学习完旧任务c时的策略对每个网络权重计算梯度的平方得到[20],用于表达策略网络中的每个权重对旧任务的重要性;θπi是任务i学习期间的策略网络权重;是学完任务i -1 时的最优策略权重。本文采用的相似性量度是广泛用于计算向量相似性关系的夹角余弦值。

权重正则化损失项Lregz受启发于online EWC方法[22-23]中将旧任务似然估计的高斯近似在网络最新的最大后验参数处重定位的做法。这意味着策略在持续学习中只需保留最近一次的最优策略权重以及不同旧任务Fisher 信息的累加结果。但online EWC 只使用一个固定的降权参数来折算所有旧任务的Fisher 信息和,这使策略更倾向于逐渐遗忘远离新任务的旧任务。与此不同,本文将任务相似性和旧任务的Fisher 信息相结合,令其成为新任务学习期间对策略网络权重更新幅度的自适应控制器。

(2) 鼓励持续学习的奖励函数。奖励函数会直接影响Q 值函数是否能公正地评价当前RL 策略,对策略的后续收敛起到重要的指导作用。面对新任务i时,每一时间步t的奖励函数包含2 项内容:针对新任务i的奖励项和针对所有旧任务的奖励项,如式(7)所示,κnew和κold是2 个经验参数。

为了计算式(7),这里定义一个可评估策略在单个任务上表现好坏的函数freward(st,at,st+1),如式(8)所示,该公式在文献[32]中被提出。

其中,Δlt表示赛车在时间步t和t+1 之间行驶的距离;ψt+1是st+1中赛车航向和道路轴线间的夹角;Δdist+1是st+1中车辆位置和道路轴线的间距。

再将获得的总奖励代入到2 个Q 值网络的损失函数中,如式(10)所示。

式中y通过式(11)来表达。

式中,α是SAC 算法的温度因子;是对应2 个Q 值网络的目标网络(target network),用于稳定Q 值网络训练,如式(12)所示。

其中,缩放因子σ∈[0,1],和θQiz分别表示Q值函数和对应的目标函数的网络权重。

在完成每次策略和Q 值网络训练时,温度因子α通过最小化式(13)来调节,H0为目标熵预设值。

最后,本文算法的伪代码总结如算法1 所示。

3 实验设置及结果分析

3.1 实验设置

本文利用3D 逼真赛车仿真平台(TORCS)[33]设计了一系列测试实验。TORCS 赛车仿真平台提供了具有多种道路形状和表面材质的道路选项。本文利用5 个各具特色的TORCS 道路场景参与实验,设计了2 条不同的任务序列,如表1 和图2 所示。相较于道路1 和2,道路3、4 和5 难度更大。尤其是道路4和5,两者单独利用传统RL训练时,均无法像其他3 条道路一样在有限训练回合内收敛。因此,任务序列1 反映了一个从易到难的持续学习过程,任务序列2 则是一个从难到易的持续学习过程。

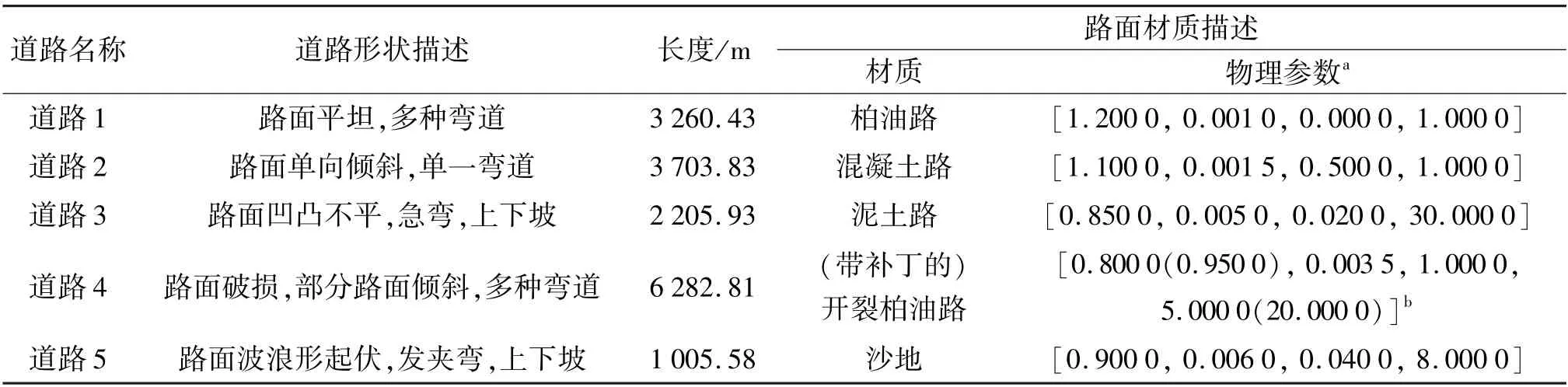
表1 所选道路的特征描述

图2 参与本文实验的TORCS 道路环境及任务序列展示

(1)基准方法。本文选择现有3 类CRL 方法中具有代表性的方法作为测试基准。经验回放基准方法采用选择性经验回放(selective experience replay,SER)方法[11]、多时间尺度经验回放(multi-timescale replay,MTR)方法[13]以及A-GEM 方法[17]。参数独立基准方法采用PNN 方法[18-19]。权重正则化基准方法采用EWC 方法[20]、online EWC (后续简称为OEWC)方法[22-23]和P&C 方法[23]。此外,本文还设计了一个精调(fine tuning,FT)基准方法,用于展示无持续学习设计的RL 算法在顺序学习多任务时的表现。在FT 方法中,每个新任务的训练利用前一个任务的最优策略初始化网络,再遵循原始SAC 算法更新。为保证比较的公平性,所有方法采用相同的策略网络结构且均以SAC 算法为CRL 的实现基础。基准方法中输入策略的任务标识嵌入向量维度与本文算法中代替嵌入向量输入策略的任务特征维度相同。

(2)消融实验。首先,讨论第1 训练阶段中任务特征维度Dim值和动力学权重生成网络的小矩阵参数U值的不同对动力学预测效果的影响。接着,检验第2 训练阶段中两项持续学习设计的贡献。该阶段的消融实验利用被命名为Oldr 和SimEWC的2 个方法进行性能分析。其中,Oldr 方法指本文算法去掉权重正则化损失、保留鼓励持续学习的奖励函数。SimEWC 方法指本文算法保留权重正则化损失、去掉鼓励持续学习的奖励函数。

(3)本文算法实现细节。特征提取器的LSTM网络有2 层且每层100 个神经元,其输入τk的时间间隔k为4,输出的任务特征维度Dim为10。动力学权重生成网络的U值为32,对应不可学习的动力学模型是一个2 层且每层256 个神经元的全连接网络。第1 训练阶段采用Adam 优化器[34],动力学损失Ldyn学习率为0.001 0,特征提取器的额外损失LE学习率为0.005 0。SAC 策略网络和评论家网络均采用尺寸为(400,300) 的两层全连接网络以及学习率设为0.000 1 的Adam 优化器。折扣因子γ和缩放因子σ分别取0.990 和0.995。奖励函数的κnew和κold均取0.5。目标熵预设值H0为动作维度的负值。最大训练回合数和每一个回合的最大步数分别是3 000和2 000。本文中所有运算均通过NVIDIA GTX 1080Ti GPU 实现。

3.2 评价指标定义

本文定义了一系列评价CRL 方法的性能指标。

(1)成功率:在100 次测试回合中,最终策略通过全部任务的回合数占比。该值越高,算法越好。

(2)平均性能(average performance,AP):如式(14)所示,Y表示总任务数,apY,y是最终策略在任务y(y≤Y) 上的性能表现。本文针对自动驾驶赛车问题的性能表现具体分为驾驶速度和稳定性两部分。评估速度时,apY,y是计算πY在任务y上所有成功测试回合的平均速度,越大越好。评估稳定性时,apY,y是计算πY在任务y上所有成功测试回合的平均车辆-道路轴线夹角绝对值,越小越好。若策略无法在一个任务上驾驶成功,根据仿真平台设置,ap的速度和稳定性部分被分别赋值为0 km·h-1和21°。

(3)后向迁移(backward transfer,BWT):如式(15)所示,apy,y表示刚学完任务y时的策略πy在该任务上的性能表现。该指标评估了策略在学习新任务后对旧任务性能的影响。积极的BWT 结果表达为速度部分大于0,且越大越好;稳定性部分小于0,且越小越好。明显消极的BWT 结果表示灾难性遗忘。

(4)前向迁移(forward transfer,FWT):如式(16)所示,ap1,y是只学习一个任务y时的策略性能。该指标评估了策略的旧任务知识对新任务学习产生的影响。积极的FWT 结果表达为速度部分大于0,且越大越好;稳定性部分小于0,且越小越好。

(5)归一化策略容量(normalized policy capacity,NPC):最终策略与学习首个任务时策略在网络容量方面的比值,NPC≥1。该值越大,网络扩张越快。

(6)归一化重放缓冲器(normalized replay buffer,NRB):CRL 方法与传统RL 方法在重放缓冲器尺寸方面的比值,NRB≥1。该值越大,数据需求越大。

(7)单步平均奖励:策略先根据式(8)计算针对单一任务的每回合奖励总和,再除以回合的总步数。

(8)精度的相对倍数变化(relative fold change in accuracy,RFCA):该指标用于分析算法第1 训练阶段的消融实验结果。如式(17)所示。RFCA 结果越高,说明对Dim或U候选值的选择越合适。

3.3 与基准方法的对比结果

表2 和3 分别展示了2 个任务序列中本文算法和基准方法的测试结果。图3 和4 分别细致展示了2个任务序列中不同方法在各个任务训练期间的单步平均奖励变化。图3 中,由于每个任务具有2 000个训练回合,因此整个持续学习过程一共有10 000个回合。图中平行于纵坐标的4 条虚线代表任务的切换。图中沿着纵坐标标注的“任务1”至“任务5”记录了各个任务在整个策略学习期间分别作为新任务和旧任务时的性能表现。所有基准方法在学习第一个任务期间没有区别,因此用一条命名为“Allbaselines”的奖励曲线统一表示。为了清晰展示多种方法的奖励曲线变化趋势,该图只在任务1的训练阶段展示出奖励曲线的置信区间,即All Baseline 曲线和本文算法曲线的阴影区域。当一个任务是新任务时,所有方法的奖励曲线记录了起始2 000 个训练回合的全部奖励数据。当该任务变成旧任务时,改为每间隔200 个训练回合测试并记录此时刻的旧任务奖励。后续奖励曲线变化图与该图的设置保持一致。根据这些图表内容,本节从以下5 个不同角度进行性能分析。

表2 任务序列1 中本文算法和基准方法的性能比较

图3 本文算法和基准方法在任务序列1 中的整个持续学习过程的奖励变化曲线

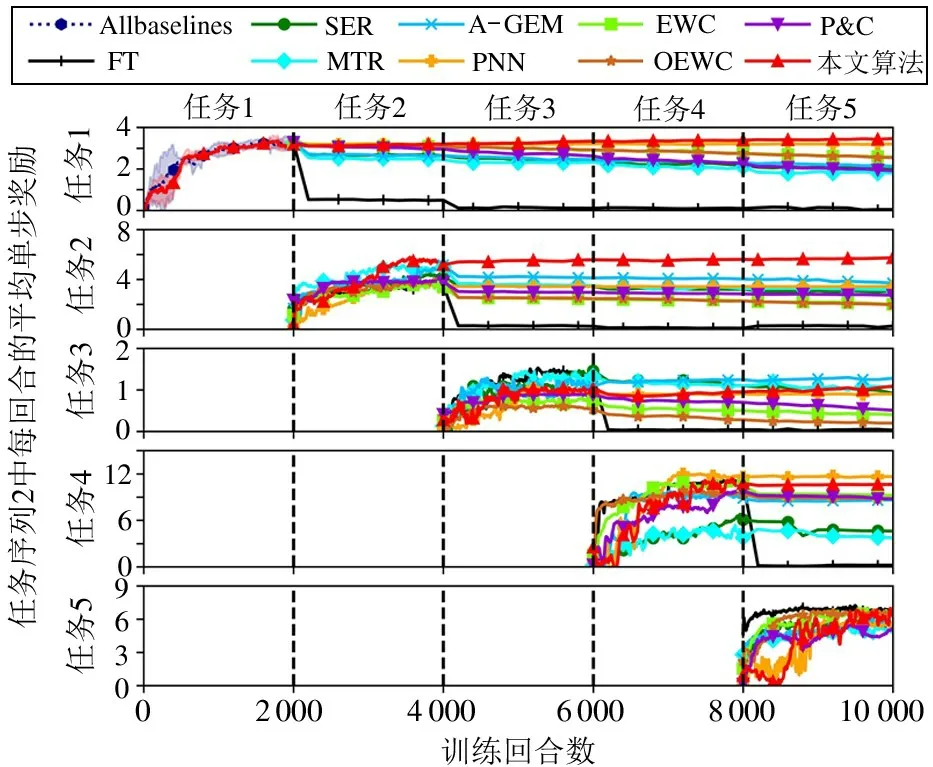
图4 本文算法和基准方法在任务序列2 中的整个持续学习过程的奖励变化曲线

(1)FT 方法在2 个任务序列上成功率均为零,且FWT 和BWT 结果均明显消极。这验证了传统RL 策略在面对多任务时普遍存在的灾难性遗忘问题,其凸显了CRL 研究的必要性。

(2)图3 和4 中,本文算法在策略训练第一个任务时的奖励曲线比基准方法具有更窄的置信区间,即训练波动更小。由于此时训练不涉及任何旧任务,该对比结果体现了本文采用的任务特征方式比基准方法中普遍使用的嵌入向量方式提供了更丰富的任务信息,令策略收敛过程更平稳。

(3)本文算法在2 个任务序列中均收获了较好的成绩。在成功率方面,本文算法的结果高于所有基准方法。在驾驶性能方面,本文算法在既不存储旧任务数据又不扩张网络的情况下,同时满足了所有CRL能力。这是其他基准方法未能做到的。从表2 和表3中可以看出:PNN 在AP 和FWT 指标上的表现是基准CRL 方法中最好的;A-GEM 方法的BWT 结果是基准CRL 方法中最好的。然而,PNN 方法的NPC=5,即策略网络随着任务增加而扩张。AGEM 方法的NRB=2,即需要额外的旧任务数据存储。本文方法能在NPC 和NRB 结果均保持最低的情况下,在任务序列1 中获得与PNN 方法最接近的平均速度;并在AP 和FWT 结果的稳定性部分以及BWT 结果的速度部分,比所有基准方法表现更好。在任务序列2 中,本文算法在AP 和FWT 结果的速度部分以及全部BWT 结果上均表现最佳。

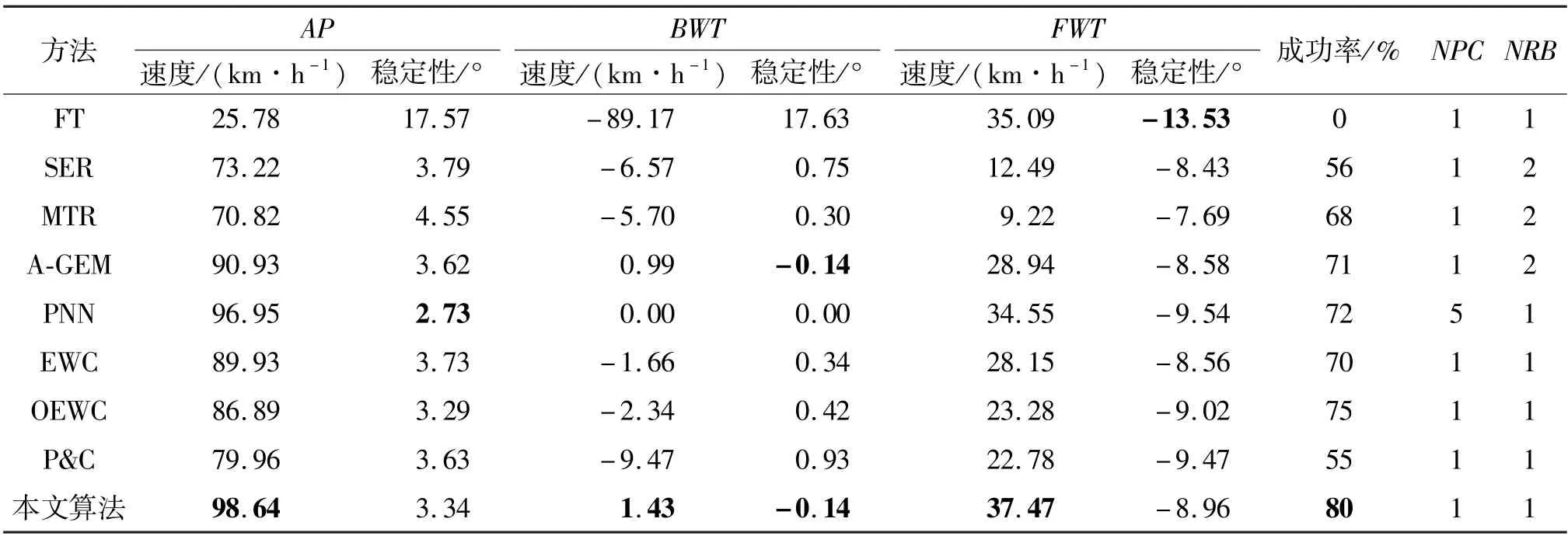
表3 任务序列2 中本文算法和基准方法的性能比较

(4)与同属于权重正则化类别的EWC、OEWC 和P&C 方法相比,本文算法能在任务序列1 的所有指标上均获得最好结果,在任务序列2 的AP 的平均速度结果、BWT 结果和FWT 的平均速度上均表现最好。结合上述第3 点分析可得,本文提出的融入任务相似性的权重正则化方法和鼓励旧任务性能不下降的奖励函数两项设计,确实能帮助策略发挥出更佳的CRL性能。同类方法中,P&C 方法表现最差,因为其利用知识蒸馏的模型压缩思想来实现策略网络的不扩张,以部分性能的下降为代价。

(5)对比2 个任务序列中同一方法性能可知,任务排序的不同会导致最终策略的收敛差异。在任务序列1 中,排在前面的任务令策略先掌握到速度较高、能应对相对单一道路特征的先验知识。与之相反,策略从任务序列2 中学到速度较低、可对应相对复杂道路特征的先验知识。任务序列1 中策略在面对道路特征更加复杂的后续任务时,更倾向获得比任务序列2 中策略具有更高驾驶速度的收敛点。

3.4 消融实验

下面将分析本文算法在2 个训练阶段的创新点。

(1) 第1 训练阶段。本阶段负责提取可描述车辆-道路动力学关系的任务特征,其中起到重要作用的2 个超参数是任务特征维度Dim值和动力学权重生成器的小矩阵参数U值。图5 和图6 分别展示了2个超参数的不同数值选择对动力学预测效果的影响。实验结果表明,尽管随着Dim值或U值取值的增大,动力学预测的精度有所提升,但其精度的提升速度远逊于训练次数的增加速度。因此,两图中的RFCA 折线都呈现出先升后降的趋势。本文选择两折线的顶点Dim=10和U=32 作为两者的最佳选择。

图5 不同特征维度Dim 对动力学预测效果的影响

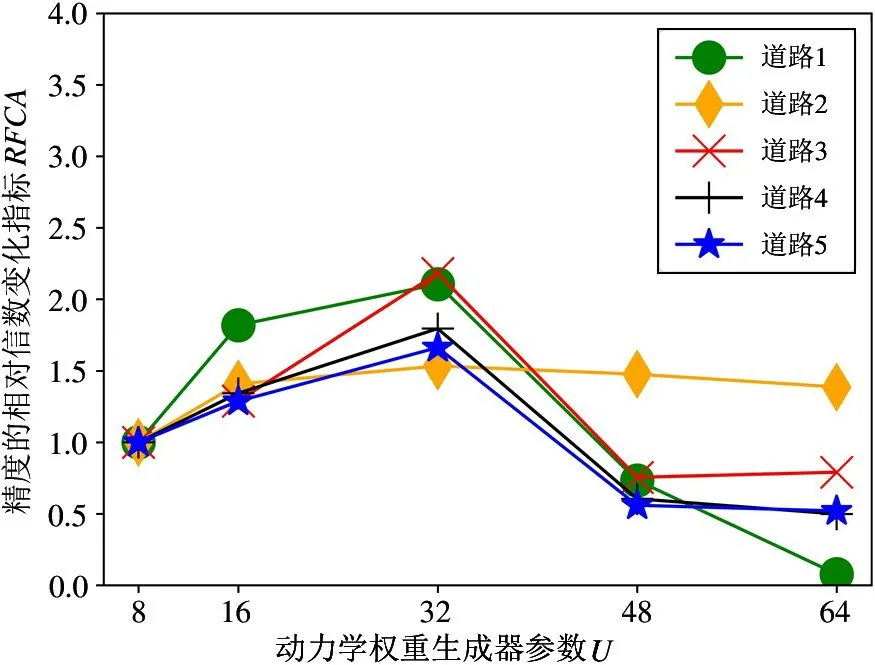
图6 不同动力学权重生成器参数U 对动力学预测效果的影响

(2) 第2 训练阶段。本阶段具有融入任务相似性的权重正则化策略损失和鼓励持续学习的RL奖励函数两项创新设计,分别通过SimEWC 和Oldr 方法实现。表4 和5 分别展示了这2 个方法的测试结果。

表4 对应本文算法第2 阶段的2 个创新点的Oldr 和SimEWC 方法在任务序列1 中的性能展示

首先,将表4、5 分别与展示基准方法性能的表2、3 进行对比。对比结果表明,在2 个任务序列中2 项创新设计均对本文算法的性能提升做出了积极贡献,且两者的结合具有协同作用。从SimEWC 方法与EWC、OEWC 基准方法的性能对比可知,SimEWC 方法在2 个任务序列中的FWT 和BWT 结果均比EWC和OEWC 方法更积极。这充分体现了任务相似性的融入对提升传统权重正则化方法在进阶CRL 能力方面的帮助,使其不再局限于仅仅解决灾难性遗忘问题。

其次,表4 与表5 中相同方法的对比展示了Oldr和SimEWC 方法在任务序列1 上均获得了比在任务序列2 上更高的平均速度、FWT 结果以及稍低的成功率。这些结果与3.2 节的第5 点分析吻合,即策略在不同任务排序下的收敛存在差异。SimEWC 方法在2 个任务序列间的平均速度变化幅度比Oldr 方法小84%,其平均稳定性变化幅度比Oldr 方法小92%。可见,SimEWC 方法对任务排序变化的敏感程度比Oldr 方法低。再对比这2 个方法的BWT 结果发现,Oldr 方法在2 个任务序列中的BWT 速度部分结果比SimEWC 方法表现更好,而BWT 稳定性部分结果是SimEWC 方法比Oldr 方法表现更好。这些结果一方面展现了Oldr 方法对持续学习的有效性,另一方面也说明了直接对策略网络权重进行自适应正则化的SimEWC 方法在实现CRL 能力方面比Oldr 方法发挥更稳定。而利用旧任务性能升降作为奖惩信号引导CRL 优化的Oldr 方法更适于搭配其他持续学习约束一起使用,可促进策略在满足持续学习需要的同时达到更好的收敛点。

表5 对应本文算法第2 阶段的2 个创新点的Oldr 和SimEWC 方法在任务序列2 中的性能展示

最后,本文利用图7 和图8 分别展示了本文算法、Oldr 以及SimEWC 方法在2 个任务序列中的整个策略训练过程。图9 可视化了道路特征间的相似性关系,用于配合SimEWC 训练曲线来共同分析任务相似性对权重正则化损失创新设计的作用。

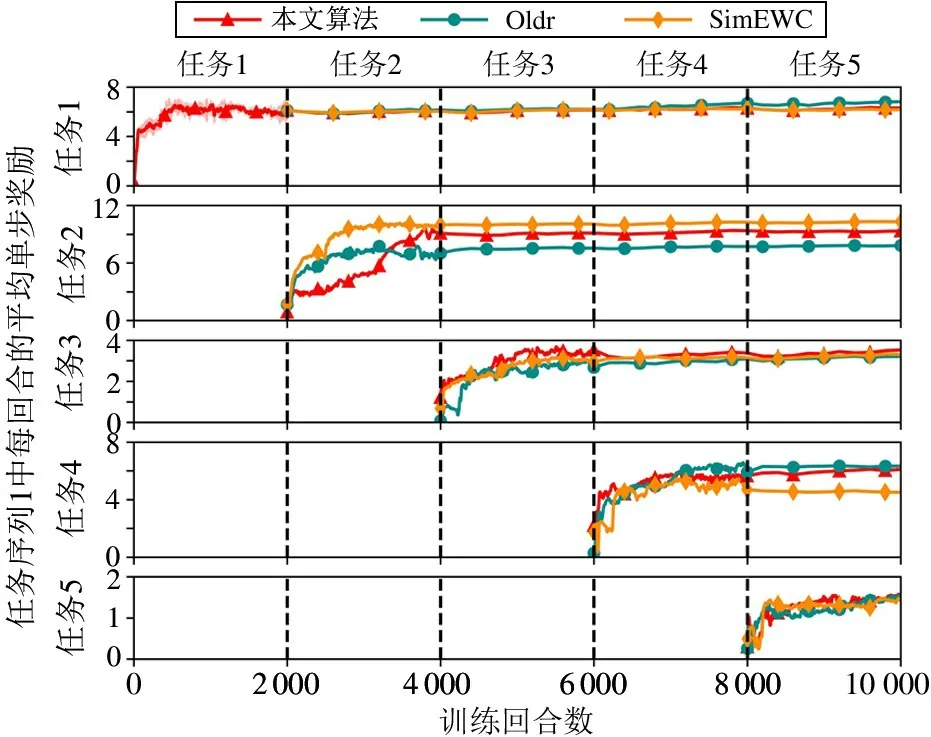
图7 本文算法、Oldr 和SimEWC 方法在任务序列1 中的整个持续学习过程的奖励变化曲线

图8 本文算法、Oldr 和SimEWC 方法在任务序列2 中的整个持续学习过程的奖励变化曲线

图9 不同道路特征之间的相似性可视化展示

当遇到与旧任务相似性低的新任务时,策略的更新过程侧重保持已有知识不被遗忘。从图9 中可以看出,道路1 和2、道路1 和5 以及道路2 和5 之间的相似性得分最低。道路1 和2、道路1 和5 之间的低相似性可以对应到图7 中SimEWC 方法的任务1 奖励曲线在任务2、任务5的学习期间只是努力保持不下降。道路2 和5 之间低相似性可对应到图7 中SimEWC 方法的任务2 奖励曲线从任务4 到任务5学习期间的明显回落趋势。上述情况也同样体现在图8 中SimEWC 方法的任务3 奖励曲线在任务4 的学习期间、任务4 奖励曲线在任务5 的学习期间。

当遇到与旧任务相似度高的新任务时,策略的更新过程追求在学习新任务的同时也提升了旧任务的驾驶性能。从图9 中可以看到,道路1、3 及4 这三者间的特征相似性是最高的。其可对应到图7 中Sim-EWC 方法的任务1 奖励曲线在任务3、4 的学习期间有明显上升趋势。与此相同的积极后向迁移表现也出现在图8 中SimEWC 方法的任务1 奖励曲线在任务2 和5 的学习期间。

4 结论

本文提出了一个融入任务相似性的CRL 算法来应对自动驾驶赛车在多变道路上的持续决策问题。该算法包括动力学特征提取方法、融入任务相似性的权重正则化方法以及维护旧任务性能不下降的奖励函数3 项设计。从而,在无需存储旧任务数据且无需扩展策略网络规模的前提下,该方法显著提高了持续决策算法的前向和后向迁移能力。这是现有方法无法做到的。仿真实验结果表明,本文算法在解决CRL问题上比其他基准方法具有更优越的综合表现。在本文工作基础上,未来工作将进一步研究如何避免由任务排序变化引起的策略收敛差异问题。