间歇性通信下多移动机器人的分布式切换预测控制①

陈嘉旻 刘安东 滕游

(浙江工业大学信息工程学院 杭州310023)

近年来,工业产业升级,单一机器人很难满足现如今的工业生产模式,便捷、高效的机器人团队协作正在克服传统工业生产的挑战,并适用于新兴行业的需求[1]。相比于单机器人,多机器人协作具有更好的鲁棒性和容错能力,同时也提高了执行任务的能力和效率。

多机器人协作通常要求多个机器人按照一定的空间轨迹协同完成任务,从而可以刻画为一个编队问题。编队控制方法有领航-跟随法[2-4]、虚拟结构法[5-7]和基于行为法[8-10]等。模型预测控制(model predictive control,MPC)作为解决分布式协作的有效控制方法,近年来被学者广泛应用于机器人编队控制中[11-13]。文献[11]针对多个非完整移动机器人编队,提出了一种基于神经动态优化的非线性MPC 控制。通过利用该方法来维持期望的领航者-跟随者的位置关系。文献[12]采用分布式MPC 和改进的虚拟结构方法,提出了一种多移动机器人编队预测控制算法,有效改善了编队结构的灵活性。文献[13]通过将路径同步参数引入到预测性能指标,提出了一种基于扩展状态观测器的分布式模型预测控制方法,采用前馈补偿策略解决了具有未知扰动下的多移动机器人编队控制问题。

上述的编队控制方法在一般的情况下都假设系统的通信不受到任何限制,即每一个机器人在编队运动中都可以获得系统中其他机器人的所有状态信息。而在实际应用场景下,移动机器人自身所携带的电池能源有限,机器人的单次使用时间受到一定的限制。并且随着移动机器人的数量增加,系统的通信负荷呈指数级增加。为此,在多机器人编队问题中还需要考虑系统的通信能力。如文献[14]针对在通信受限的情况下多机器人编队的问题,提出了一种分散控制率,其中将信息流分为了2 种时间尺度,并且随着信息交互时间的延长,允许间歇性信息丢失,以降低通信负载。文献[15]提出了一种事件触发控制算法,以显著减少编队控制更新,消除多智能体节点间的连续通信。文献[16]为了解决在通信拓扑切换下车辆队列的协同控制问题,提出了一种分布式MPC 策略,利用该方法保证在车辆运动时系统的稳定性。以上的分布式MPC 控制算法大多采用静态拓扑结构或给定顺序的切换拓扑结构,其中切换拓扑结构算法都没有给出切换律的设计方法。并且当系统工作状态不符合给定的切换律时,其控制系统将无法保证稳定。为此本文将在切换拓扑结构算法的基础上,给出切换律的设计方法。

本文针对机器人编队运动中的通信交互问题展开研究,提出了多移动机器人在间歇通信下的编队控制算法。首先,通过将切换拓扑策略描述为间歇性通信,将多机器人编队建模为一类带有路径参数同步约束项的切换系统模型,并针对名义模型提出了一种分布式切换预测控制方法,然后给出各子系统切换时稳定的条件以及控制器的设计方法。其次,结合级联控制系统的方法设计路径参数同步控制器,使多移动机器人在完成路径跟踪的同时,进一步完成路径参数同步。最后,通过给定的通信控制序列,多移动机器人完成子系统之间的切换,每一次切换代表不同的通信拓扑结构,从而达到机器人间歇通信的目的。

1 问题描述

1.1 运动学模型

考虑一个具有n个移动机器人的编队系统,其中移动机器人以期望的队形来跟踪预先设定的参考路径Γi(τi) 上的虚拟机器人,τi为预先设定的路径参数。在惯性坐标参考系下,机器人i的运动学模型表示为

其中,φi为移动机器人前行方向相对于X轴的方向角,ui=(vi,ωi)T表示移动机器人i的线速度和角速度向量。

移动机器人在惯性坐标系下的跟踪误差向量表示为

其中,ηi=[xie,yie,φie]T为虚拟机器人i的状态向量。

令虚拟机器人i的速度向量为uri=(vri,ωri)T,对式(2)求导可得如下的跟踪误差模型:

令ui=[vricos(φri -φi)-vi,ωri -ωi]T,ηi=[xie,yie,φie]T,将系统式(3)在平衡点处(ηi=0,ui=0) 线性化可得如下的连续状态空间模型:

其中,Ai=I +ApiT,B=BpT。为了简单起见,本文考虑的参考路径Γi(τi) 为圆形。由于Γi(τi) 是关于τi的函数Γi(τi)=col(ηi(τi),φi(τi)),为了实现协同控制问题,需要通过设置τi的更新方程,来完成实际的编队结构和虚拟编队结构的协调[13]。不失一般性,τi的更新方程设置为

其中,εi为路径参数更新方程的控制输入,Δεi为其控制增量,δi为系数矩阵。

综上所述,本文考虑的多移动机器人编队控制问题可以描述为如下2 个控制任务:

(1)路径跟踪任务。首先,让虚拟移动机器人沿着给定的参考路径运动,当编队结构中的路径参数达到同步时,虚拟机器人将位于期望的编队结构上,最后使实际的移动机器人能够跟踪上相应的虚拟移动机器人,即

(2)编队路径参数同步任务。确保所有的路径参数τi(t) 同步,从而使虚拟机器人维持期望的虚拟编队结构:

图1 编队路径设置示意图

1.2 通信约束

由1.1 节可知,本文的控制目标为完成路径跟踪和路径参数同步,因此在设计控制器时,分别引入路径跟踪控制器和路径参数同步控制器

为了方便设计控制器,采用分布式预测控制方法。首先,根据文献[17]将式(10)转化为如下形式:

为关于路径参数的矩阵,本文将其视为系统的扰动;θij表示不同子系统之间通信的通或断,当通信连接时取1,反之取0,由θij构成的矩阵θ可表示不同的通信拓扑结构;σ(k)∈{0,1,2,…} 表示由拓扑结构决定的切换信号,即σ(k)是θ(k) 的一个映射;Kiσ(k)为切换信号依赖的控制器增益。

由式(13)可知,Φ(k)中只含有路径参数,不含有系统状态¯η(k)。为此可将系统式(13)看成一个名义系统部分和系统扰动Φ(k) 组成。因此,名义系统模型为

本文的任务分别是路径跟踪任务和路径参数同步任务。由控制器式(9)可知,本文的控制器设计按照这2 个任务可分为2 部分,即分别针对系统的名义模型式(14)和路径参数式(6)设计路径跟踪控制器和路径参数同步控制器。由于本文将系统式(13)分解为名义系统式(14)和干扰项Φ(k),而系统式(14)与路径参数εi无关,从而可以并行设计路径跟踪控制器u1i和路径参数同步控制器u2i。因此,本文的目的考虑具有间歇性通信的多机器人编队系统式(13),针对名义系统式(14)采用分布式切换预测控制方法设计控制器增益Kiσ(k)(k);针对路径参数同步更新方程式(6)采用分布式预测控制器设计路径参数更新方程控制增量Δεi(k),保证多机器人系统完成编队任务。

2 基于MPC 的编队同步控制

2.1 分布式切换MPC 控制算法

系统采用级联控制系统的控制方法,首先设计切换MPC 控制器来完成机器人的路径跟踪,之后在此基础上设计一个MPC 控制器,用于完成机器人的路径参数同步任务。

本节的目的是通过切换MPC 策略为系统式(13)的名义模型式(14)设计一个稳定控制器。通过切换MPC 控制算法,使移动机器人在通讯切换时仍然保持各子系统稳定,并获得最佳的系统性能。

为此,假设切换系统式(14)的每个子系统都存在一个稳定的MPC 控制器,同时每个子系统与要最小化的性能指标相关联,每个子系统根据预先设定的通信序列进行切换,同时代价函数之间进行切换。为了给系统式(14)设计一个稳定化的控制器,考虑以下有限时域最优控制问题:

问题1:

其中,N是预测步长,Piσ(k)是正定对称矩阵,Kiσ(k)是在k时刻需要设计的状态反馈控制器增益。

定义1 考虑系统式(14),若存在正常数c和λ,使得对于任意的初始条件(t0)∈Rn,系统的解满足

则系统式(14)指数稳定并具有指数衰减率,其中α=k -k0。

定义2 对任意ξ2>ξ0≥0,令Nσ(ξ1,ξ2) 表示切换信号σ在间隔(ξ1,ξ2) 内的切换次数。若存在ξa>0和N0≥0 使得不等式Nσ(ξ1,ξ2) ≤N0+成立,那么,ξa称为切换信号σ的平均驻留时间,N0称为抖动界。

定理1 如果存在正标量λ <1和μ >1,正定矩阵Pi(k)>0,Kil(k),l=0,1…,使得以下不等式成立:

证明1 如果不等式(18)成立,则有:

由于不等式Υil(k +1,N) ≤λ2Υil(k,N),Υia(k,N) ≤μΥib(k,N),对于切换信号σ(k),由式(20)～(22)可得以下不等式关系:

基于定理1 中的稳定性条件,状态反馈控制器的存在条件由以下定理给出。

定理2 给定正标量λ <1和μ >1,考虑以下半正定规划问题:

如果该问题有解,则存在稳定化的状态反馈控制器使得切换系统指数稳定且具有指数衰减ρ(λ,其控制器增益其中,注:不等式(18)～ (20)是切换系统稳定的充分条件,分别对应式(28)、(32)、(31),若优化问题式(28)有解,则可以保证不等式(18)～(20)成立。

证明首先选择如下的李雅普诺夫函数。

对式(33)应用Schur 补引理可得以下不等式:

综上,算法1 如下。

步骤1 初始化。设置k=0,并选择常数μ和通信切换序列。

步骤2 信息采集。在k时刻,通过通信网络测得各移动机器人的状态。

步骤3 优化。求解最小化问题minζi(k) 得到相应的Kil(k)和Pil(k)。

步骤4 参数调整。调整参数λ,把步骤3 求得的Kil(k)和Pil(k) 代入式(32)判断不等式是否成立。如果不等式成立,则Kil(k) 为各子系统的稳定化控制器的增益。如果不成立则继续调整参数λ,以判断不等式(32)是否成立。

步骤5 滚动时域。令k=k +1,跳转至步骤2。

2.2 路径参数同步预测控制

本节的目的是在上一节的基础上,为系统的扰动设计控制器,即路径参数控制器,使移动机器人完成编队任务。为了提高多移动机器人的路径跟踪性能,在较短的时间内使移动机器人位于期望位置,并提高系统的动态性能,将同步参数和路径参数的控制增量引入预测性能指标,则每个移动机器人的路径参数可以进行单独优化,将其目标函数定义为

其中,τi(k +j| k)、τj(k +j| k)和Δεi(k +j| k) 分别为τi(k +j)、τj(k +j)和Δεi(k +j)在k时刻的预测值,M为预测时域取值为1,τr为给定的标量参数。Wi >0和Si >0 为给定的权重矩阵,Gi为给定的耦合项的权重矩阵,为移动机器人集合。

在k时刻,通过最小化MPC 性能指标,可以得到最优解,以下为最小化问题

以上优化问题为典型的QP 问题,依据一阶KKT(Karush-Kuhn-Tucker)条件,可以求得最小化问题式(36)的解为

由于式(37)中包含了邻居子系统输入,可采用迭代策略求解,即邻居子系统输入采用上一迭代时刻值替代,从而将式(37)增广后可得:

其中,Ω=diag{Ω1,…,Ωn},Ψ=(Ψ1,…,Ψn)T,Δε(k)=(Δε1(k),…,Δεn(k))T,G(i,j)=p为迭代次数。因此,通过选择合适的权重矩阵Wi >0、Si >0和Gi,使得ρ(Ω-1G)<1,则式(38)是收敛的。同时名义系统式(14)是渐近稳定的,从而有

综上,算法2 如下。

步骤1 初始化。在k=0 时刻,设置迭代次数p=0 输入路径参数τi以及参数μ和λ。

步骤2 信息交互。移动机器人i通过算法1设置的通讯序列,间歇性地将自身的状态信息与控制信息传递给相邻移动机器人j,同时也获得相邻机器人的状态和控制信息。

步骤3 优化。机器人i通过式(36)计算出其局部最优解。

步骤4 参数调整。调整参数Wi、Si和Gi,使得ρ(Ω-1G) <1。并令(k)(k) 并结束迭代,跳转至步骤5,否则令p=p +1 跳转至步骤2 继续执行。

步骤5 滚动时域。令k=k +1,跳转至步骤2。

3 仿真验证及分析

为了验证本文提出算法的有效性,仿真时考虑由3 个移动机器人组成的编队系统,其编队队形为等边三角形结构,边长为3 m。同时在给定的通信序列下,移动机器人进行通信切换,最后使移动机器人能够沿着给定的参考路径,并保持编队结构进行编队运动。多移动机器人的具体参数设置如下:参考路径是分别是半径4 m、3 m 和1 m 的同心圆。

移动机器人的初始状态为

切换系统的权重矩阵选取为

路径跟踪优化的权重矩阵为

路径参数的初始值为

采样周期为0.2 s,并给出一组切换序列如下:

其中通信切换系列中的0、1、2 分别对应图2 中的3种通信拓扑结构。

图2 机器人通信拓扑结构示意图

从序列中可以得知,各子系统切换次数为53次,通过算法1 可以得到μ=1.1,λ=0.993 2;通过子系统的切换顺序和平均驻留时间的定义,可以得到tα=400/53=7.547 2。因此在这种情况下,可以进一步得到tα >=Inμ/2In(1/λ)=6.984 2,平均驻留时间满足定理1 的式(23),那么系统指数稳定且具有指数衰减率ρ(λ,ta)=仿真结果如图3 和图4 所示。图3 为移动机器人的状态误差曲线,机器人在40 s 左右可以完成路径跟踪。图4 为误差控制输入。

图3 移动机器人状态误差曲线

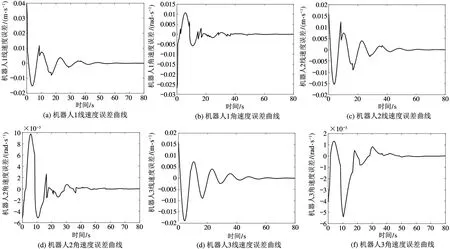
图4 移动机器人误差控制输入

图5中τ12、τ23和τ13分别为路径参数τ1和τ2之差、τ2和τ3之差以及τ1和τ3之差。移动机器人1和移动机器人2 最后收敛的角度差是60 °,移动机器人2 和移动机器人3 最后收敛的角度差是60 °,移动机器人1 和移动机器人3 最后收敛的角度差是0 °。移动机器人图中的路径参数误差在40 s 左右趋于0,那么移动机器人在40 s 后可以实现期望的编队运动。

图5 移动机器人路径参数误差曲线

图6 为移动机器人运动轨迹的仿真图。图中分别选取了3 组不同时刻的编队运动情况,t=0 s,t=4 0 s和t=80 s。t=0 s时为初始时刻,虚线三角形为虚拟机器人形成的期望编队结构,实线三角形为实际机器人形成的初始编队结构。显然在初始时刻实际机器人没有形成期望的编队结构,当t=40 s 时3 组移动机器人基本形成期望的编队结构,与虚拟机器人的轨迹基本重合。最后选取t=80 s 时刻,可以看到多移动机器人可以在间歇通信的情况下,稳定地保持期望的编队结构运动。

图6 移动机器人编队运动轨迹图

4 结论

本文针对在间歇通信条件下的编队控制问题,提出了一种分布式切换预测控制方法。利用分布式MPC 方法,结合级联控制系统方法,分别针对系统的名义模型部分和路径参数同步项设计了控制器,并给出系统指数稳定的充分条件以及平均驻留时间。机器人编队系统在切换拓扑策略下,实现间歇通信的目的。仿真实验表明,多移动机器人在通信受限的情况下,利用本文所提出的算法,机器人仍然可以较好地完成编队运动,从而达到了在大规模机器人协同控制中降低通信负载的要求。